Похожие презентации:
Конус. Понятие конуса и его элементы
1.
КонусСеврюкова Евгения Анатольевна
учитель математики
МБОУ СОШ № 2 с.п. «Село Хурба»
2.
Конус в переводе с греческого «konos»означает «сосновая шишка».
С конусом
древности.
люди
знакомы
с
глубокой
Большой трактат о конических сечениях
был
написан
Аполлонием
Пергским–
учеником
Евклида,
который
создал
великий труд из 15 книг под названием
«Начала». Эти книги издаются и по сей
день, а в школах Англии по ним учатся до
сих пор.
3.
Понятие конуса и его элементыКонус вращения
Конические сечения
Площадь боковой поверхности конуса
Площадь полной поверхности конуса
Объем конуса
Усеченный конус
Задачи по теме «Конус»
4.
Определение:тело,
ограниченное
конической поверхностью и кругом с
границей L, называется конусом.
P
F
L
x
5.
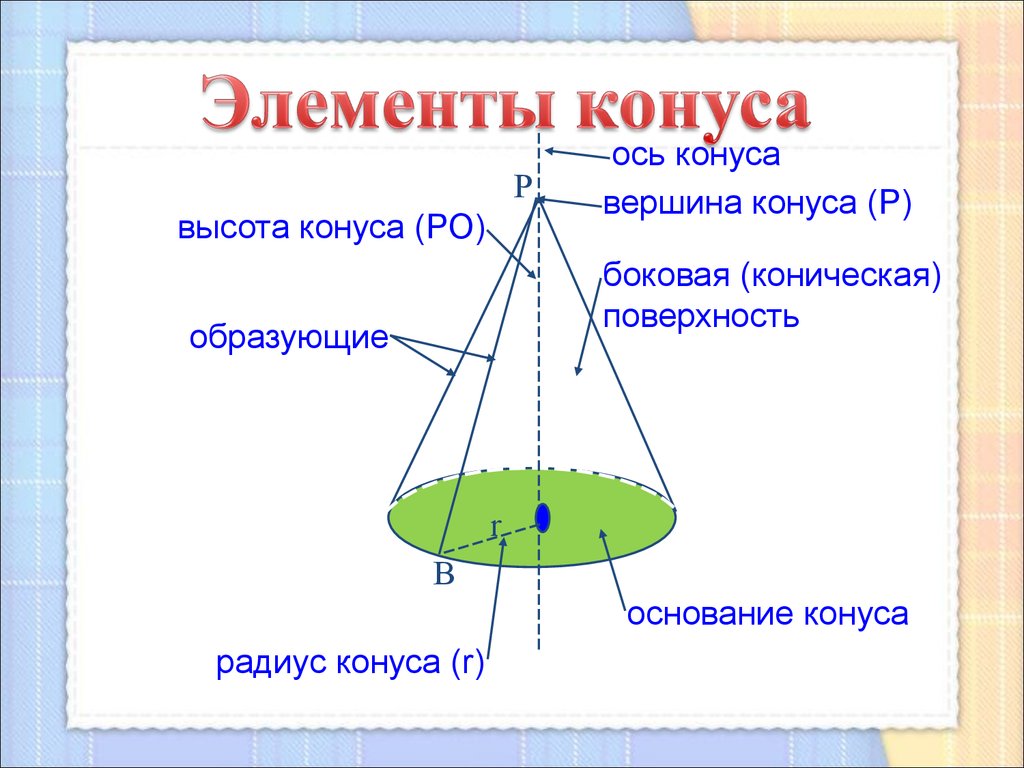
Pвысота конуса (РО)
ось конуса
вершина конуса (Р)
боковая (коническая)
поверхность
образующие
r
B
основание конуса
радиус конуса (r)
6.
Прямой круговой конусявляется объединением
всех равных друг другу
прямоугольных треугольников, имеющих общий
катет. Поэтому можно
сказать, что он получается
при
вращении
прямоугольного треугольника вокруг одного из
катетов – оси конуса.
А
В
С
С2
С1
7.
ОСЕВОЕ СЕЧЕНИЕВ сечении равнобедренный
треугольник, основание которого
диаметр основания конуса, а
боковые стороны – образующие
конуса.
СЕЧЕНИЕ, ПЕРПЕНДИКУЛЯРНОЕ
ОСИ КОНУСА
Сечение, перпендикулярное к
оси конуса представляет собой
круг,
секущая
плоскость
перпендикулярна оси конуса.
РО1М1 ~ РОМ
r1 = РО1/РО*r
8.
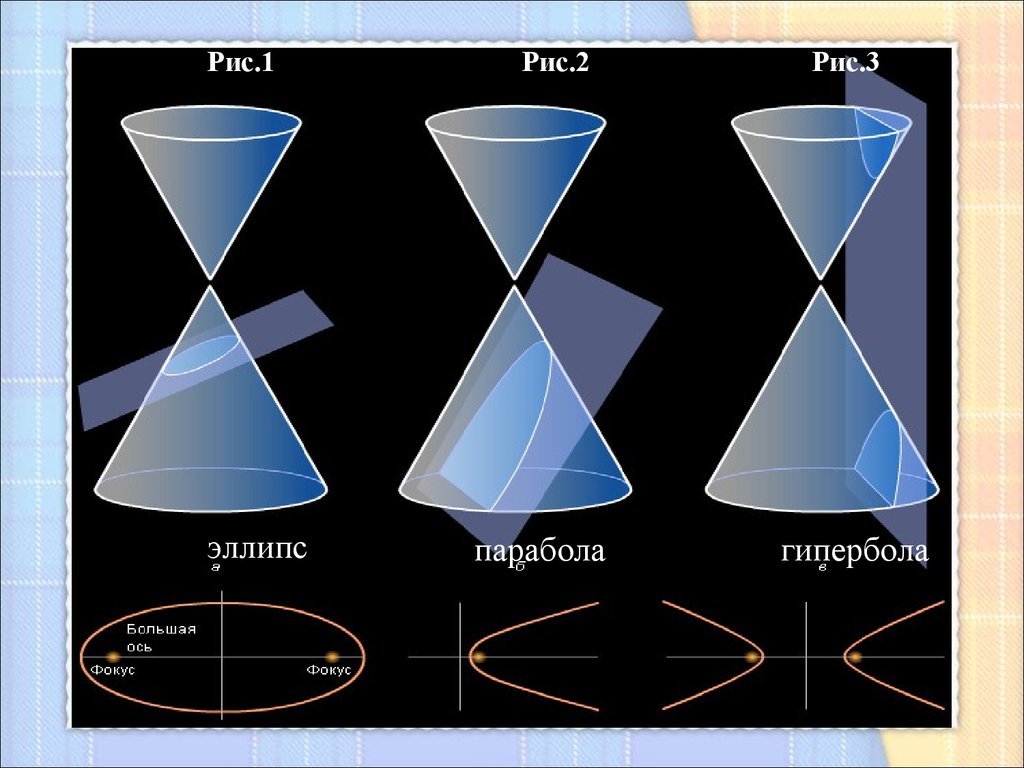
Рис.1эллипс
Рис.2
парабола
Рис.3
гипербола
9.
За площадь боковой поверхности конусапринимается площадь его развертки (конической
поверхности).
1) Sбок =
πl
360
2
P
α
2) Sбок = π rl
A
B
10.
Площадь боковой поверхности конуса равнапроизведению половины длины окружности
основания на образующую. Площадью полной
поверхности конуса называется сумма площадей
боковой поверхности и основания.
Sкон = π r (l+r)
11.
SоснVконуса
=1
3
2
πR H
12.
высотабоковая
поверхность
образующая
основания
радиусы
Усеченным конусом называется пересечение
конуса с полупространством, содержащим
основание конуса и ограниченным плоскостью,
которая параллельна плоскости основания конуса
и пересекает данный конус.
13.
Задача 1Высота конуса равна диаметру его основания.
Найти отношение площади его основания к площади
боковой поверхности.
Решение:
Пусть радиус основания конуса равен R, тогда
2
площадь основания Sосн = π R , а высота конуса 2R.
В
SOA:
√ SO
SA =
2
2
+ OA =
√(2R)
2
2
S
√5
+R =R
√5
Итак, l = SA = R
2
Тогда Sбок = π Rl = π R
Искомое отношение:
√5
Sосн
Sбок
2
=
πR =√ 5
2
πR√ 5 5
A
O
14.
Задача 2Авиационная бомба среднего калибра дает
при взрыве воронку диаметром 6 м и
глубиной 2 м. Какое количество земли (по
массе) выбрасывает эта бомба, если 1 м3
земли имеет массу 1650 кг?
Решение:
V=1
3
2
πR H
=1
3
π * 32 * 2 =6 π (м 3 )
O 3м
A
2м
P = 1650*6*3,14 ≈ 31086 кг ≈ 31 т.
Ответ: P = 31 т.
B
C
15.
Задача 3Смолу для промышленных нужд собирают,
подвешивая конические воронки к соснам.
Сколько
воронок
диаметром
10 см
с
образующей 13 см нужно собрать, чтобы
заполнить 10-литровое ведро?
Дано:
Решение.
коническая воронка V = 1 π R 2H = 1 π* 25 * 12 =100 π(см3 ) =
3
3
D = 10 см
= 100 π см 3 = 0,1π дм3 .
L = 13 см
O
5
A
C
V–?
(H =√ 13 - 5
2
13
B
n = 10
0,1
=
2
= 12
)
100 = 100 ≈ 31,8
π 3,14
Ответ: n ≈ 32 воронки.












 Математика
Математика








