Многокритериальные задачи принятия решений. Метод анализа иерархий (МАИ)

1.

Многокритериальные задачи
принятия решений
Содержание лекции:
Метод анализа иерархий (МАИ)

2.

Метод анализа иерархии (МАИ) систематическая процедура решения сложных
проблем путем декомпозиции их на более
простые составляющие части, иерархического
представления и дальнейшей обработки
последовательности суждений ЛПР или
экспертов.
В вершине иерархии помещается проблема.
Промежуточные уровни содержат критерии, от
которых зависят последующие уровни. На
самом нижнем уровне находятся альтернативы

3.

Метод
основан
на
парных
сравнениях
альтернативных
вариантов
по
различным
критериям с использованием девятибалльной
шкалы и последующим ранжированием набора
альтернатив по всем критериям и целям.
Взаимоотношения между критериями учитываются
путем
построения
иерархии
критериев
и
применением парных сравнений для выявления
важности критериев и подкритериев.
Применение МАИ позволяет включить в иерархию
все
имеющиеся
у
эксперта-аналитика
по
рассматриваемой
проблеме
знания
и
воображение. Метод достаточно прост и хорошо
отражает интуитивные представления экспертов.

4.

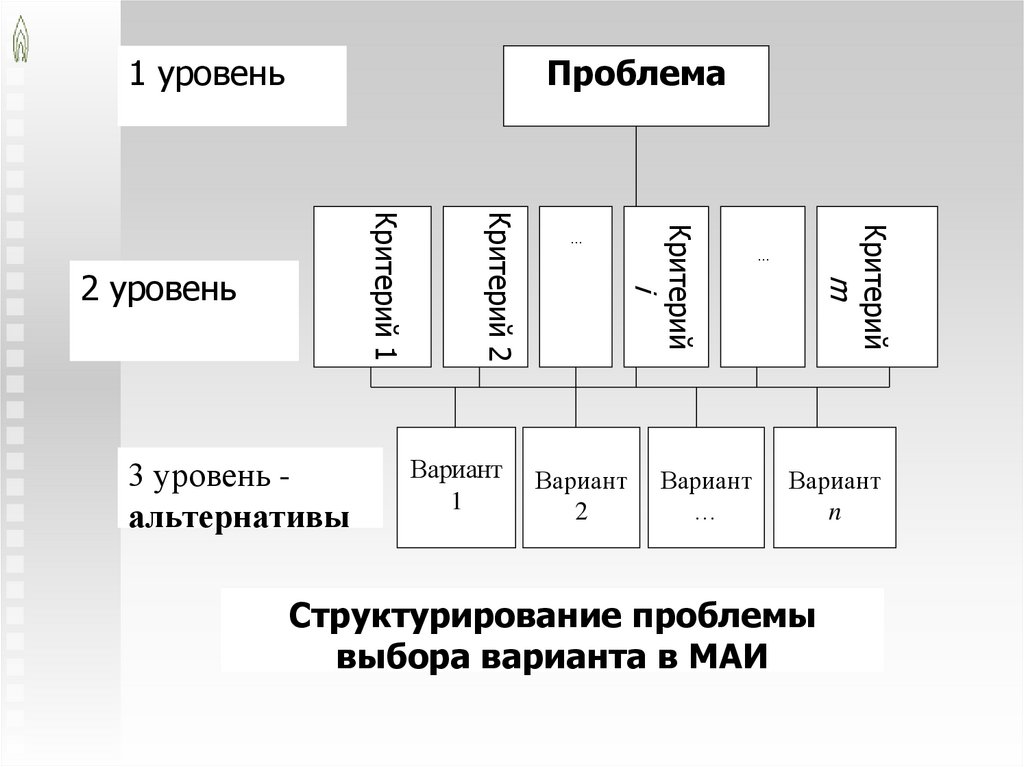
1 уровень
Проблема
Критерий
m
Критерий
Вариант
1
…
i
3 уровень альтернативы
Критерий 2
Критерий 1
2 уровень
…
Вариант
2
Вариант
…
Вариант
n
Структурирование проблемы
выбора варианта в МАИ

5.

Реализация метода
1.
2.
3.
Структуризация задачи. Строится дерево иерархии – иерархическая
структура, которая имеет несколько уровней. Его вершиной является
общая цель (глобальный критерий). Затем структурируются частные
(локальные) критерии. На самом нижнем уровне дерева иерархии
находятся альтернативы.
ЛПР (эксперты) на всех уровнях иерархии (кроме первого) определяет в
каждой группе критериев весовые коэффициенты ее членов, которые
характеризуют их относительную важность с точки зрения критерия
следующего, более высокого уровня. Альтернативы также сравниваются
между собой по отдельным критериям с целью определения веса каждой
из них. Для определения коэффициентов важности критериев либо
критериальной ценности альтернатив проводятся парные сравнения всех
элементов группы по заданной балльной шкале. Их результат
представляется в виде квадратной числовой матрицы, называемой
матрицей парных сравнений. Затем вычисляется вектор весовых
коэффициентов и проводится проверка согласованности сравнений.
На основе найденных весовых коэффициентов вычисляются оценки всех
альтернатив по заданным критериям. Лучшей считается альтернатива,
имеющая самую высокую суммарную оценку.

6.

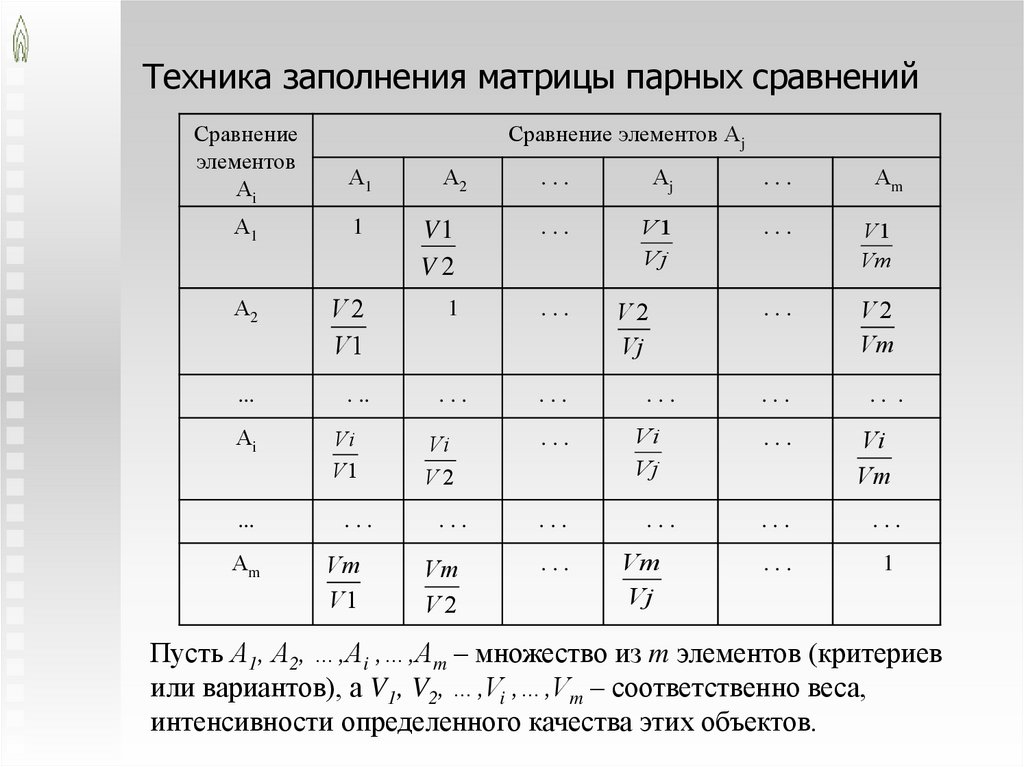
Техника заполнения матрицы парных сравнений
Сравнение
элементов
Аi
Сравнение элементов Аj
А1
А2
...
Аj
...
Аm
А1
1
V1
V2
...
V1
Vj
...
V1
Vm
А2
V2
V1
1
...
...
V2
Vm
...
. ..
...
...
...
...
.. .
Аi
Vi
V1
Vi
V2
...
Vi
Vj
...
Vi
Vm
...
...
...
...
...
...
...
Аm
Vm
V1
Vm
V2
...
Vm
Vj
...
1
V2
Vj
Пусть А1, А2, …,Аi ,…,Аm – множество из m элементов (критериев
или вариантов), а V1, V2, …,Vi ,…,Vm – соответственно веса,
интенсивности определенного качества этих объектов.

7.

В основу процедуры парных сравнений положена шкала
относительной важности от 1 до 9. Эксперты на основе своей
квалификации и опыта производят качественное сравнение Аi
элементов друг с другом. Обозначим любое число из этой шкалы,
кроме 1, как с.
Тогда Vi / Vj = 1, если i = j, и Vi / Vj = с, если вес (качество) Vi > Vj
(числитель предпочтительнее знаменателя) и Vi / Vj
= 1/с, если вес знаменателя
предпочтительнее веса числителя, то есть Vj > Vi.
Любая матрица парных сравнений должна быть обратно
симметричной, т. е. все ее элементы должны удовлетворять
следующему условию:
cji = 1 / cij .

8.

Из группы матриц парных сравнений формируются
локальные приоритеты. Для этого вычисляется множество
собственных векторов методом геометрической средней:
Wi m (ci1 ) (ci 2 ) ... (ci m )
для i-й строки
i = 1,2,…,m
Полученное множество векторов затем нормализуют к
единице, получая тем самым вектор приоритетов (R):
W
Ri m i
Wi
i 1
где m = количество критериев.

9.

Оценка однородности суждений
Для оценки однородности суждений используется специальный
индекс, который рассчитывается по формуле
max m
ОС =
1
E (О)
m 1
где ОС – однородность суждений; max – максимальное
собственное значение матрицы; m – размерность матрицы; E(О) –
средняя согласованность индекса однородности случайным образом
составленной матрицы парных сравнений (таблица)
n
max Aj R j
j 1
E(О)
Размер матрицы
1
2
3
4
5
6
7
8
9
Согласованность
0
0
0,58
0,9
1,12
1,24
1,32
1,41
1,45

10.

В соответствии с алгоритмом МАИ для окончательного
выбора сценария необходимо произвести свертку частных
рангов в глобальный ранг (Rг) вариантов (сценариев).
Глобальный ранг находится как сумма произведений ранга
критерия на ранг сценария по данному критерию.
Максимальный ранг (оценка) альтернативы является
оптимальным решением

11.

Выпускник института должен принять решение о своей будущей
работе. Проанализировав влияющие на решение факторы (критерии),
он отобрал, по его мнению, наиболее существенные:
величина заработной платы (зарплата),
привлекательность работы (работа),
перспективы продвижения (карьера),
риск увольнения (риск).
Нужно оценить три альтернативы (возможные варианты работы):
А - частная фирма (менеджер): привлекательность работы мала, но
самый высокий заработок. Перспективы карьеры неясны, риск
увольнения велик.
В - институт (научный сотрудник): работа интересная, но зарплата
самая низкая. Перспективы научной карьеры хорошие, риск
увольнения мал.
С - государственное учреждение (чиновник): работа менее интересная,
чем в институте, но зарплата выше. Перспективы карьеры имеются,
риск увольнения невелик.

12.

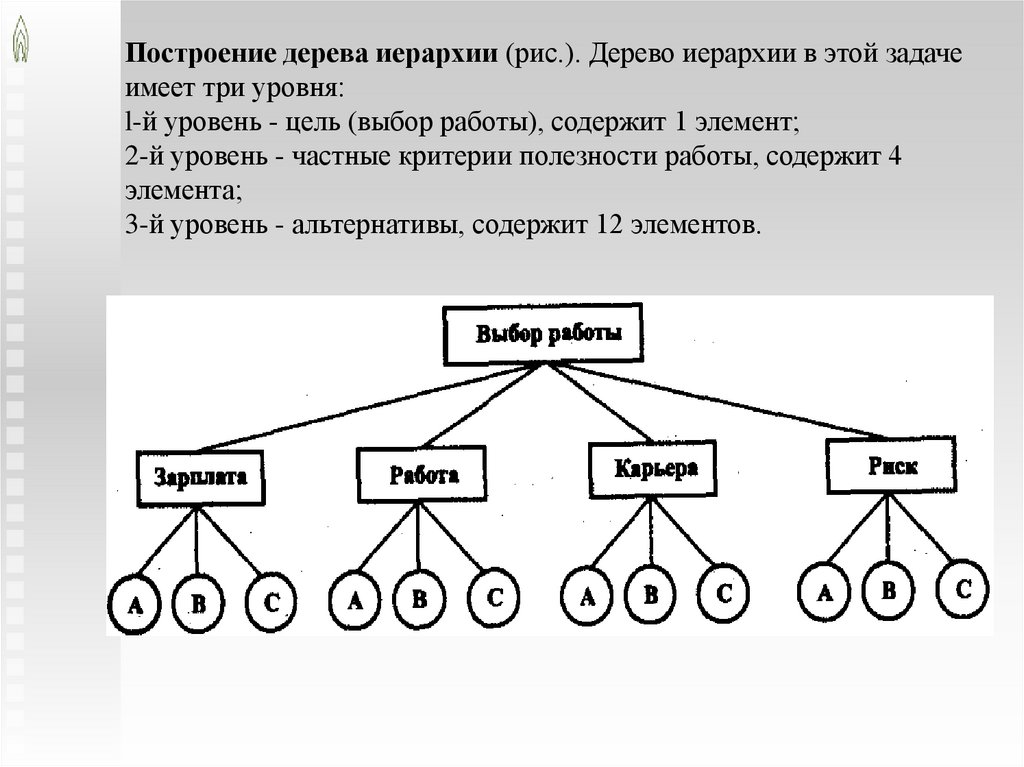
Построение дерева иерархии (рис.). Дерево иерархии в этой задаче
имеет три уровня:
l-й уровень - цель (выбор работы), содержит 1 элемент;
2-й уровень - частные критерии полезности работы, содержит 4
элемента;
3-й уровень - альтернативы, содержит 12 элементов.

13.

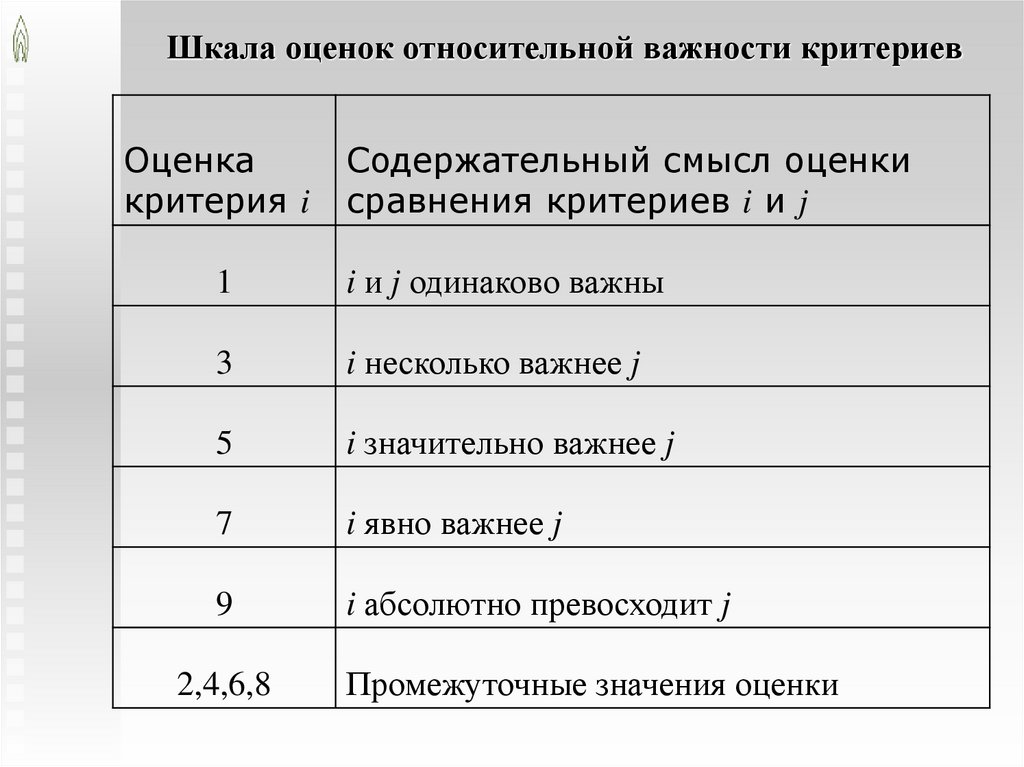
Шкала оценок относительной важности критериев
Оценка
критерия i
Содержательный смысл оценки
сравнения критериев i и j
1
i и j одинаково важны
3
i несколько важнее j
5
i значительно важнее j
7
i явно важнее j
9
i абсолютно превосходит j
2,4,6,8
Промежуточные значения оценки

14.

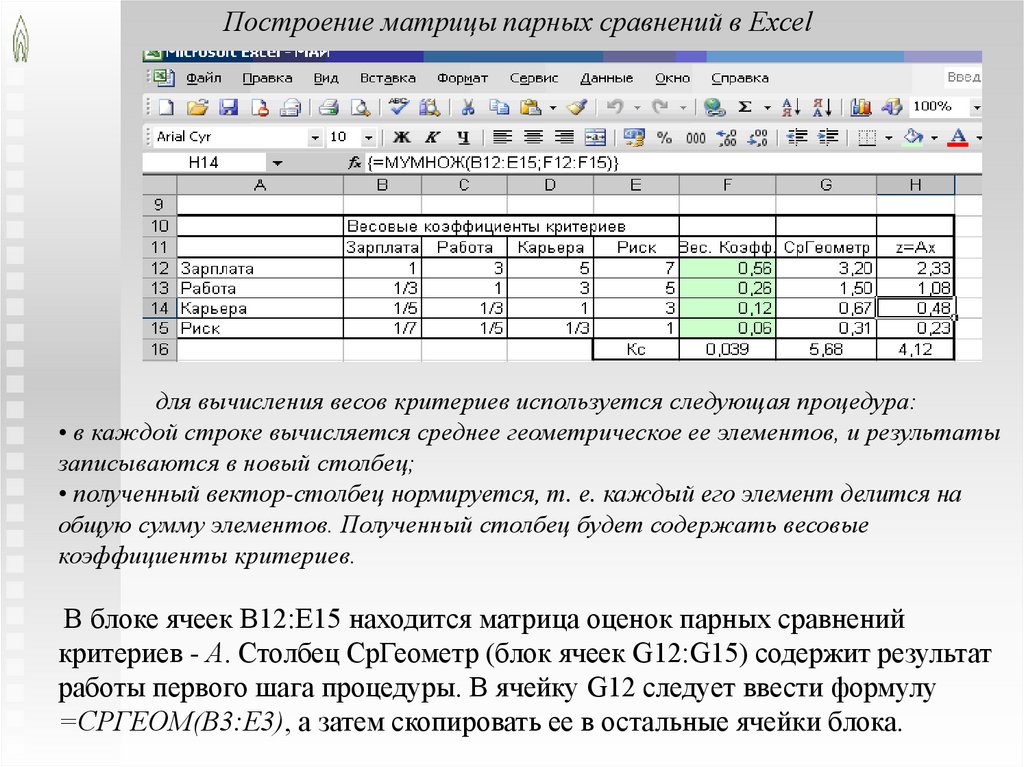
Построение матрицы парных сравнений в Excel
для вычисления весов критериев используется следующая процедура:
• в каждой строке вычисляется среднее геометрическое ее элементов, и результаты
записываются в новый столбец;
• полученный вектор-столбец нормируется, т. е. каждый его элемент делится на
общую сумму элементов. Полученный столбец будет содержать весовые
коэффициенты критериев.
В блоке ячеек В12:Е15 находится матрица оценок парных сравнений
критериев - А. Столбец СрГеометр (блок ячеек G12:G15) содержит результат
работы первого шага процедуры. В ячейку G12 следует ввести формулу
=СРГЕОМ(В3:Е3), а затем скопировать ее в остальные ячейки блока.

15.

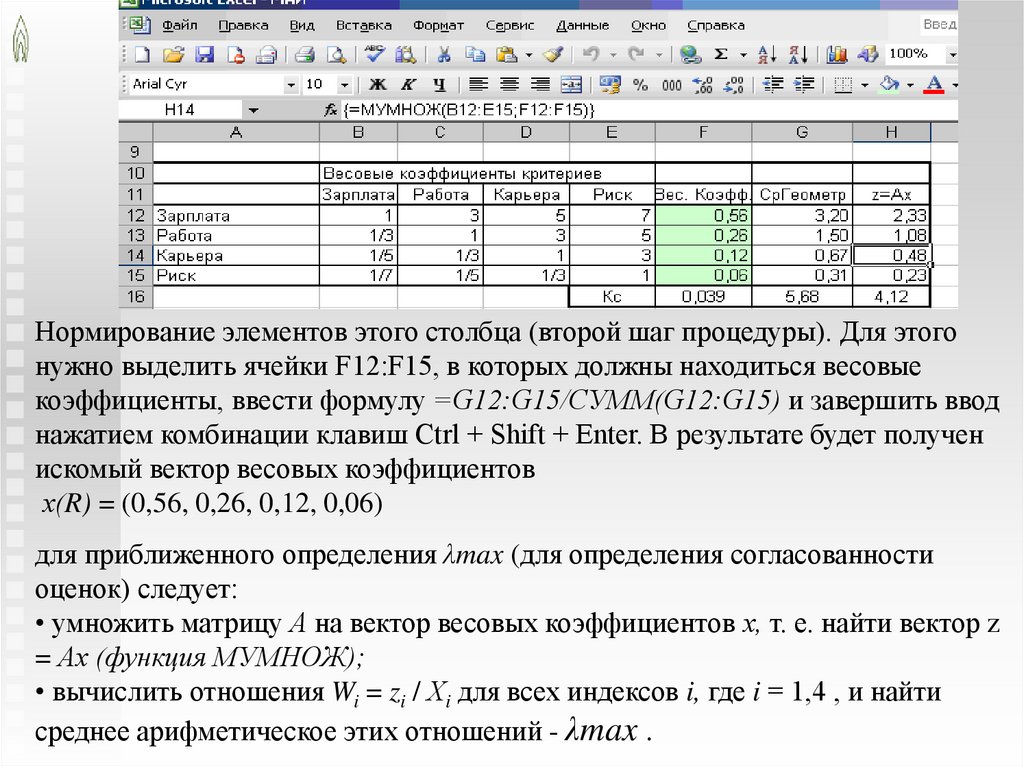
Нормирование элементов этого столбца (второй шаг процедуры). Для этого
нужно выделить ячейки F12:F15, в которых должны находиться весовые
коэффициенты, ввести формулу =G12:G15/CУММ(G12:G15) и завершить ввод
нажатием комбинации клавиш Ctrl + Shift + Enter. В результате будет получен
искомый вектор весовых коэффициентов
х(R) = (0,56, 0,26, 0,12, 0,06)
для приближенного определения λmax (для определения согласованности
оценок) следует:
• умножить матрицу А на вектор весовых коэффициентов х, т. е. найти вектор z
= Ах (функция МУМНОЖ);
• вычислить отношения Wi = zi / Хi для всех индексов i, где i = 1,4 , и найти
среднее арифметическое этих отношений - λmax .

16.

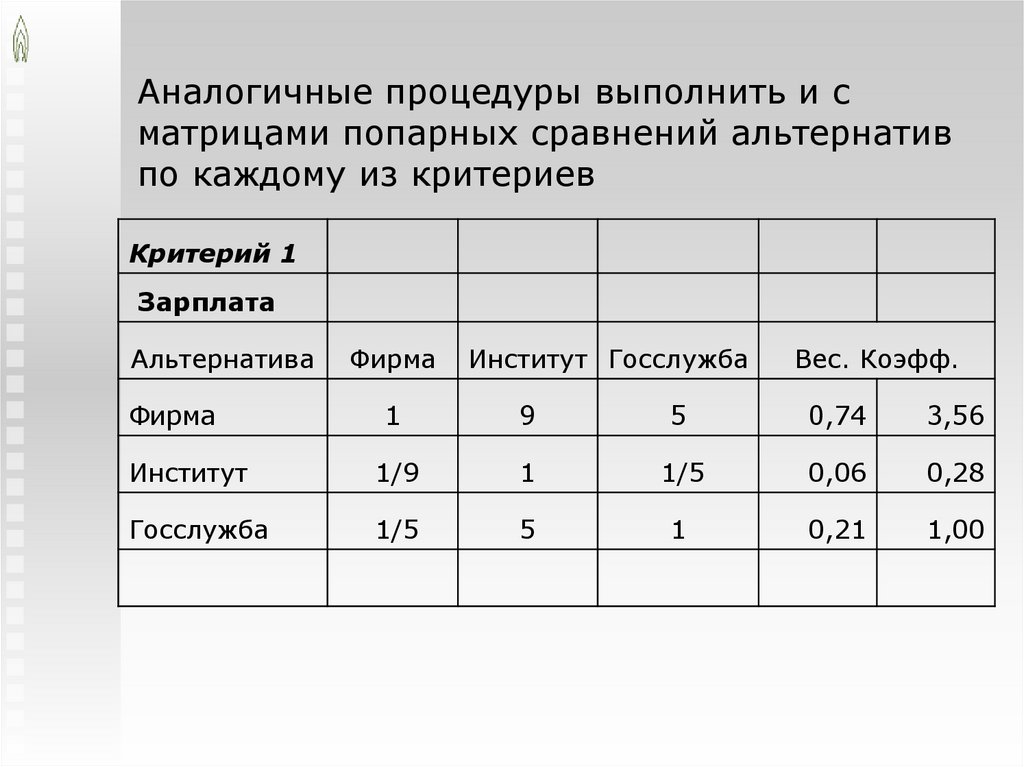
Аналогичные процедуры выполнить и с
матрицами попарных сравнений альтернатив
по каждому из критериев
Критерий 1
Зарплата
Альтернатива
Фирма
Институт Госслужба
Вес. Коэфф.
Фирма
1
9
5
0,74
3,56
Институт
1/9
1
1/5
0,06
0,28
Госслужба
1/5
5
1
0,21
1,00

17.

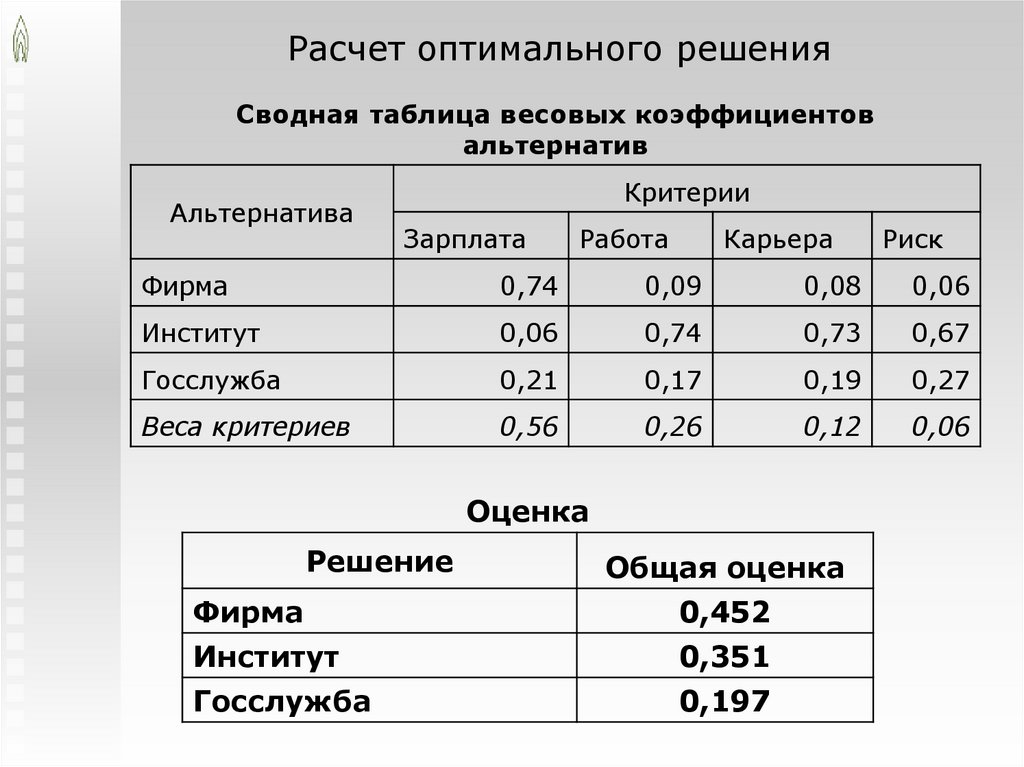
Расчет оптимального решения
Сводная таблица весовых коэффициентов
альтернатив
Альтернатива
Критерии
Зарплата
Работа
Карьера
Риск
Фирма
0,74
0,09
0,08
0,06
Институт
0,06
0,74
0,73
0,67
Госслужба
0,21
0,17
0,19
0,27
Веса критериев
0,56
0,26
0,12
0,06
Оценка
Решение
Общая оценка
Фирма
0,452
Институт
0,351
Госслужба
0,197