Похожие презентации:
Модели атомных ядер
1.
2.
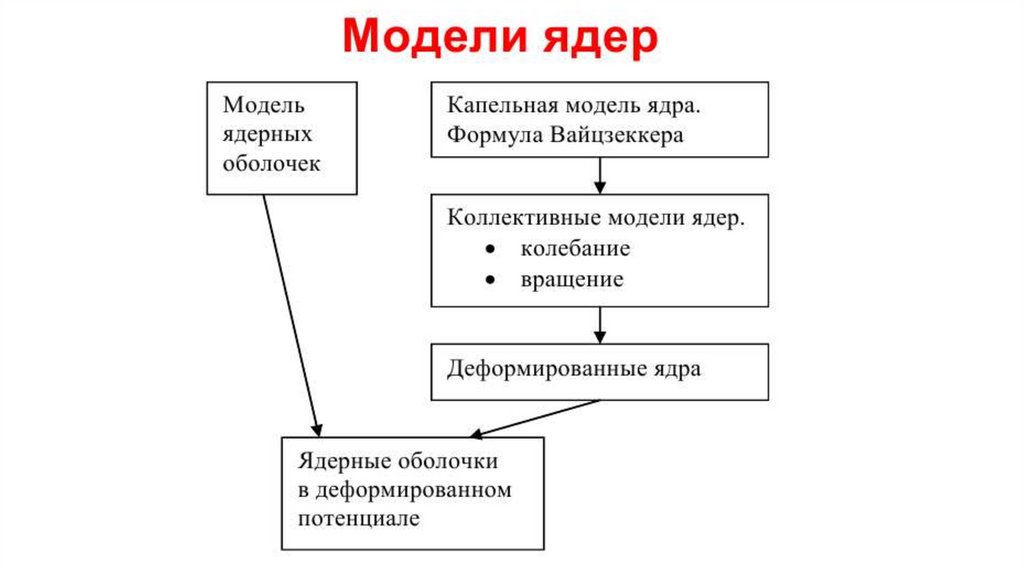
3.
4.
5.
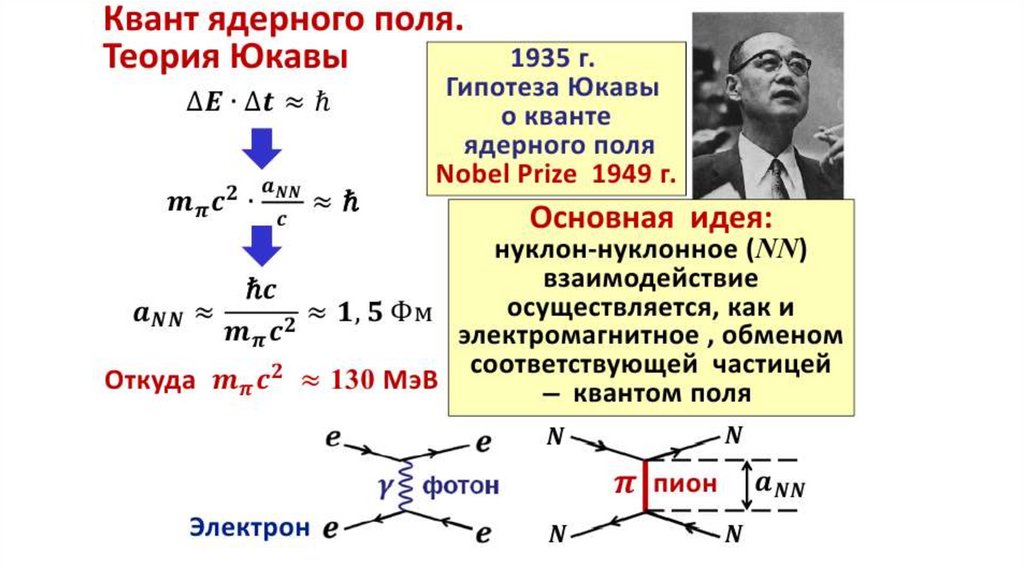
Взаимодействие между нуклонами6.
Капельной моделью не описываются1. Индивидуальные характеристики ядер такие, как спин и связанный с ним
магнитный момент, четность, энергии возбуждения
2. эффект спаривания нуклонов и влияние его на энергию связи (все четно-четные
ядра в основном состоянии имеют нулевые спины и магнитные моменты)
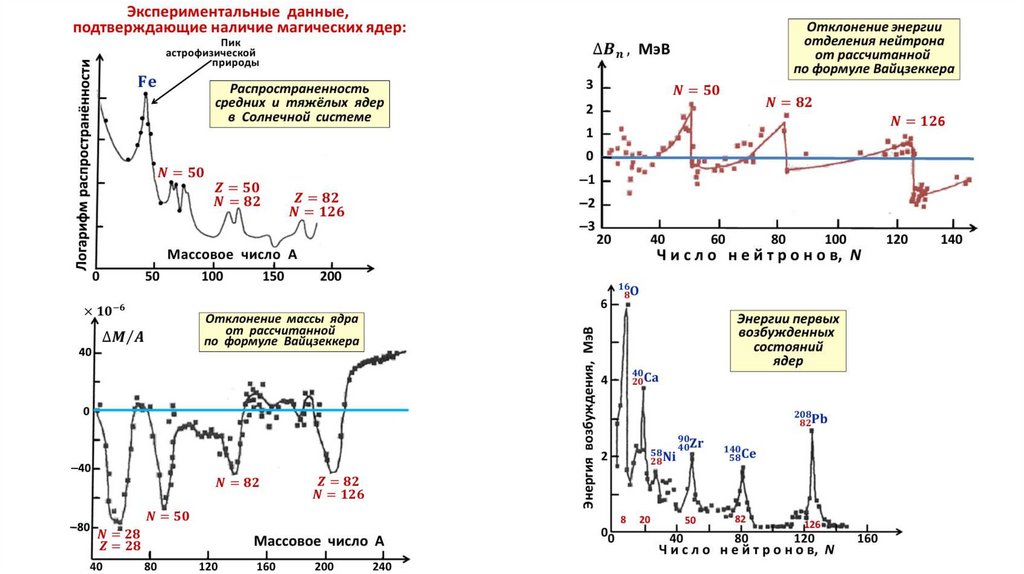
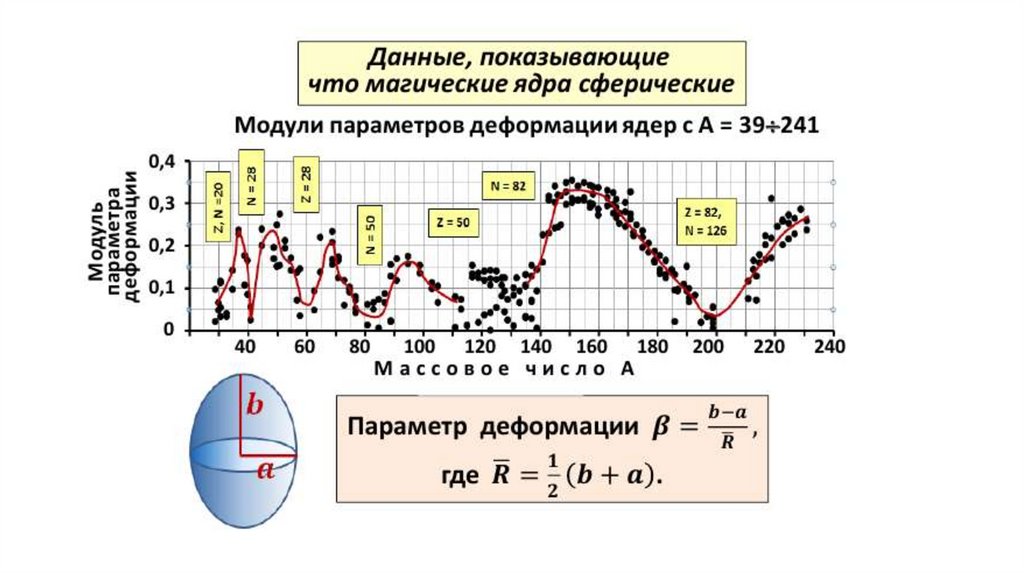
3. ядра с числом протонов или нейтронов, равным 2, 8, 20, 50, 82 или 126, особенно
устойчивы и гораздо больше распространены в природе, чем их ближайшие
соседи по N-Z-диаграмме.
Идея –
периодическое изменение свойств атомов в зависимости от числа
электронов.
Подобно магическим ядрам, оболочки атомов, содержащие 2, 10, 18, 36,
54 или 86 электронов (инертные газы) являются особо устойчивыми
7.
8.
9.
10.
11.
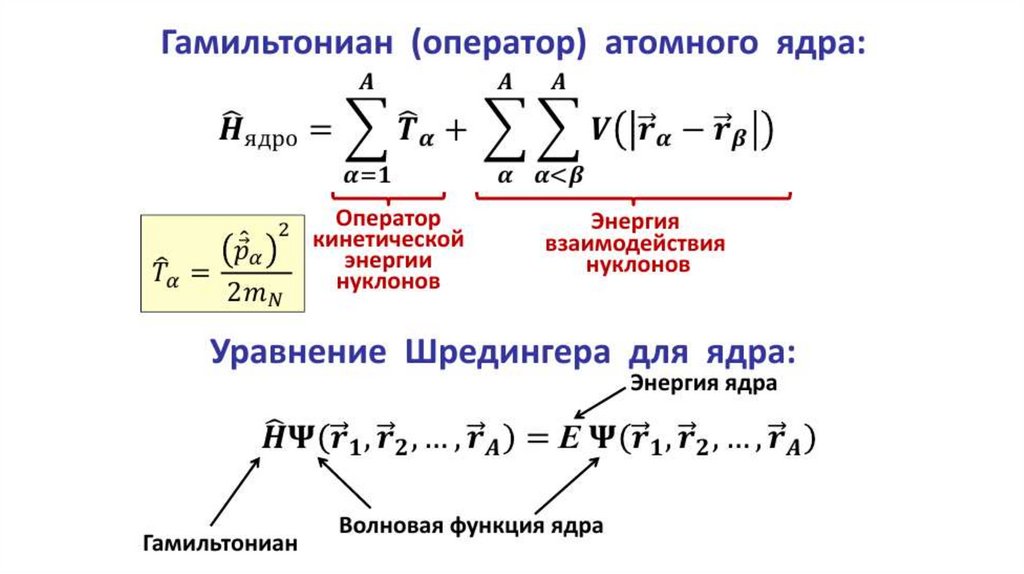
Оболочечная модель ядраИдея – использовать достижения квантовой механики для описания свойств
атомных ядер и физических эффектов при ядерных взаимодействиях
Функция ψ(x, y, z) ≡ ψ(r) - волновая функция
В квантовой механике уравнение движения сводится к описанию временной
эволюции волновой функции ψ(r) –уравнение Шредингера
i
U r
t
2
2
где Δ – дифференциальный оператор Лапласа
2 2 2
2 2 2
x
y
z
12.
Оболочечная модель ядраДля расчета стационарных
Шредингера сводится к виду
энергетических
состояния
уравнение
2
U r E
2
U r
- стационарное уравнение Шредингера
- потенциал взаимодействия
Решение стационарного уравнения – собственные значения энергии
13.
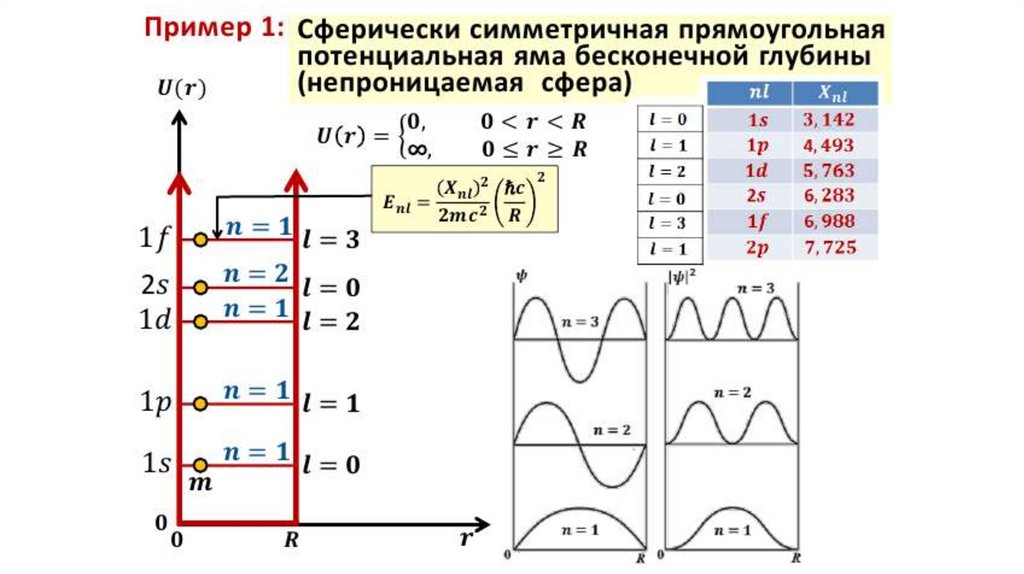
Пример - Частица в прямоугольной потенциальной ямепрямоугольная потенциальная яма бесконечно большой глубины и конечной
ширины a
Потенциальная энергия частицы (с массой μ) при x < 0 и x > a должна быть
бесконечно велика, волновая функция за пределами ямы обращается в нуль.
Внутри ямы, где U(x) = 0, уравнение Шредингера
обозначение
2 E
k 2
2
2 d 2
2 E
2 dx
14.
уравнение Шредингераd
2
k 0
2
dx
2
решением является функция
Asin kx B cos kx
обращается в нуль на границах
потенциальной ямы
a A sin ka 0
n A sin
nx
a
В=0
ka n
n = 1, 2, 3 и т.д
Число n называется квантовым числом и
равно целому числу длин полуволн де
Бройля частицы
p
Первые уровни энергии и волновые функции
частицы в одномерной прямоугольной
потенциальной яме бесконечной глубины
n
En
2 a 2
2 2 2
15.
16.
Задача о стационарном движении частицыв потенциальном поле U(r), зависящем только от длины радиусвектора r и не зависящем от углов θ и φ (т.н. центральное поле)
используем
2 2
2 U x x Ex x
2 x
U
r
U
x
U
y
Разделение переменных
2 2
2 U y y E y y
2 y
Собственная функция ψ в этом случае будет произведением
x x y y
собственное значение энергии
E Ex E y
17.
задача о стационарном движении частицы в потенциальном поле U(r)универсальные собственные функции ψ(θ, φ) определяются
1. моментом импульса частицы
L r p
2. проекцией вектора L на выбранную ось Lz
L2 2l (l 1), l 0, 1, 2...
Lz ml , ml 0, 1,..., l
Числа l и ml называются орбитальным и магнитным квантовыми числами.
L L1 L 2 ,
l1 l2 l l1 l2
18.
19.
20.
21.
22.
23.
24.
Квантовое число – четность (P)Система является четной (P = +1) или нечетной (P = –1) в зависимости от того, сохранится
или изменится знак волновой функции системы при смене знаков всех пространственных
координат.
Четность изолированной системы, как и энергия, импульс и момент импульса,
сохраняется.
При движении частицы в центральном поле ее волновые функции с четным
орбитальным числом l четны, с нечетным – нечетны.
где π1 и π2 – т.н. внутренние четности частиц
P12 1 2 1
l1 l 2
Для протона принята πp = +1. Четности всех других частиц определяют относительно
протона на основании закона сохранения четности. Так, внутренняя четность электрона
πe = +1, нейтрона πn = +1, а фотона πγ = –1.
25.
26.
27.
28.
29.
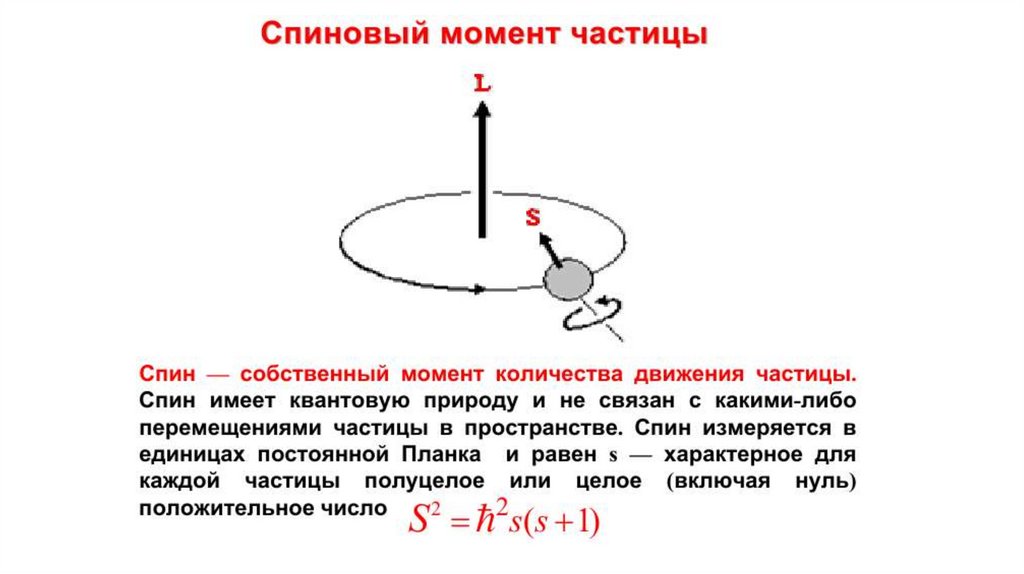
Квантовое число спин - собственный момент импульса частицы SS s ( s 1)
Величина спина
характеризуется числом s, принимающим, в отличие от орбитального квантового числа,
не только целые (0, 1, 2…), но и полуцелые (1/2, 3/2, 5/2 …) значения. Часто именно это
число s и называют спином частицы
2
2
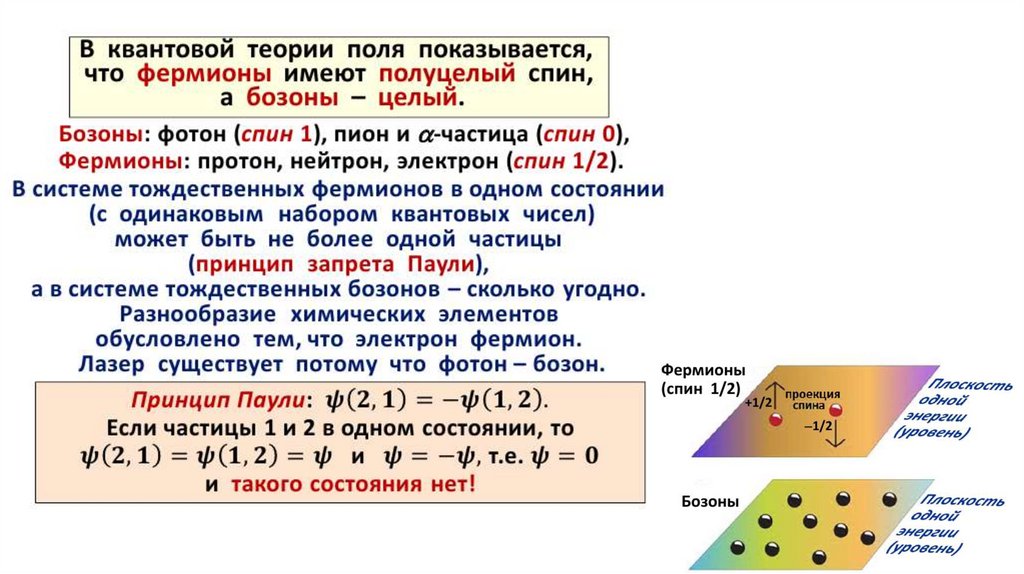
Частицы с целым спином называют бозонами, с полуцелым – фермионами
Электрон, протон и нейтрон (s = ½) принадлежат к группе фермионов. Фотон (s = 1)
является бозоном
Все фермионы подчиняются принципу Паули, согласно которому в любом квантовом
состоянии может находиться не более одного фермиона данного вида.
Для бозонов подобного ограничения не существует.
30.
31.
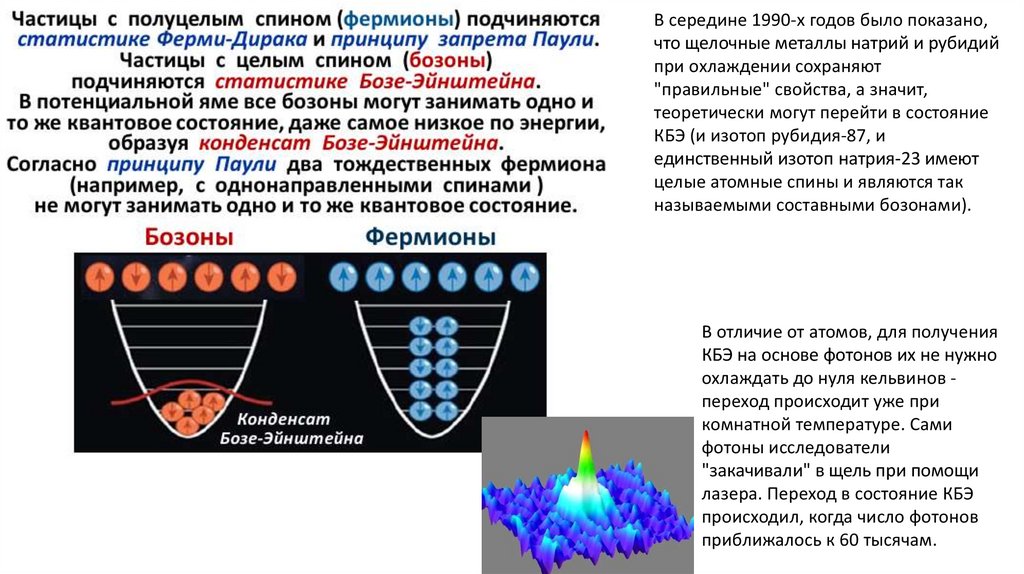
В середине 1990-х годов было показано,что щелочные металлы натрий и рубидий
при охлаждении сохраняют
"правильные" свойства, а значит,
теоретически могут перейти в состояние
КБЭ (и изотоп рубидия-87, и
единственный изотоп натрия-23 имеют
целые атомные спины и являются так
называемыми составными бозонами).
В отличие от атомов, для получения
КБЭ на основе фотонов их не нужно
охлаждать до нуля кельвинов переход происходит уже при
комнатной температуре. Сами
фотоны исследователи
"закачивали" в щель при помощи
лазера. Переход в состояние КБЭ
происходил, когда число фотонов
приближалось к 60 тысячам.
32.
33.
34.
35.
Волновая функция системы одинаковых фермионов антисимметричнапо отношению к перестановке координат любых двух частиц (т.е.
меняет свой знак при такой операции).
Волновая функция системы одинаковых бозонов симметрична
относительно такой перестановки
36.
37.
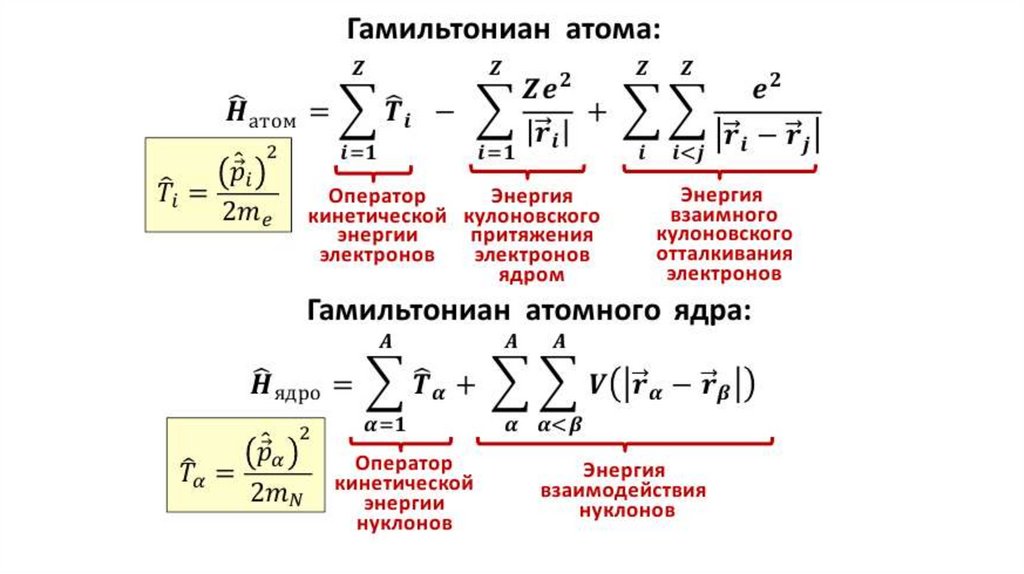
модель электронных оболочек базируется на двух основных положениях:1) в атоме имеется центральное поле кулоновского притяжения электронов к
ядру;
2) электроны проводят большую часть своего времени вдали друг от друга.
В отличие от атома
1. У ядра нет выделенного силового центра.
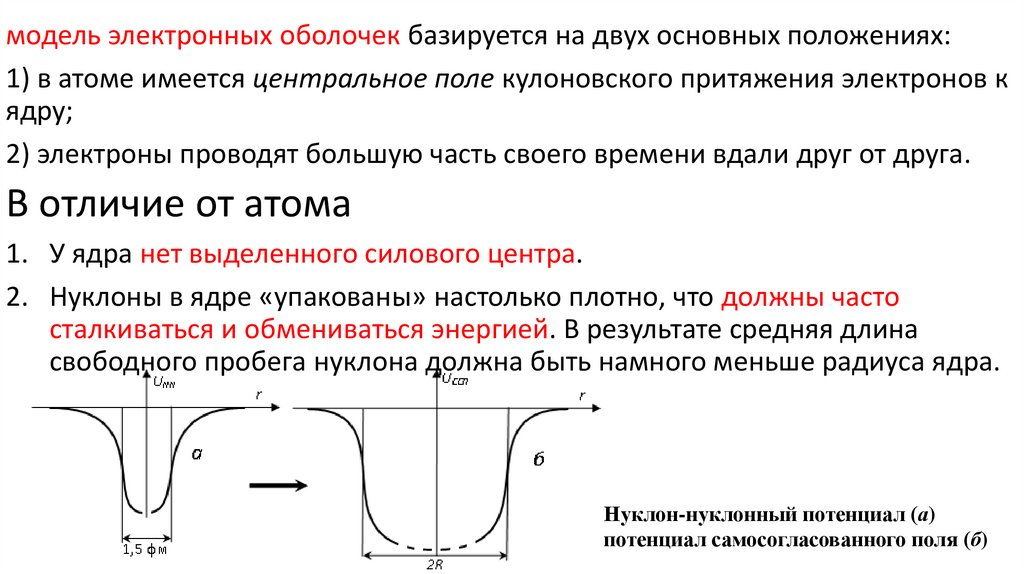
2. Нуклоны в ядре «упакованы» настолько плотно, что должны часто
сталкиваться и обмениваться энергией. В результате средняя длина
свободного пробега нуклона должна быть намного меньше радиуса ядра.
Нуклон-нуклонный потенциал (а)
потенциал самосогласованного поля (б)
38.
39.
Уровни энергии нуклона в центральном полеОболочечная модель была впервые сформулирована в 1949 г. (М. Гёпперт-Майер и др.)
в оболочечной модели рассматривается движение каждого нуклона в отдельности, т.е. последняя является
одночастичной
Движение нуклона в самосогласованном поле UССП описывается стационарным уравнением Шредингера
2
U ССП E
2
Потенциал самосогласованного поля подбирается эмпирически.
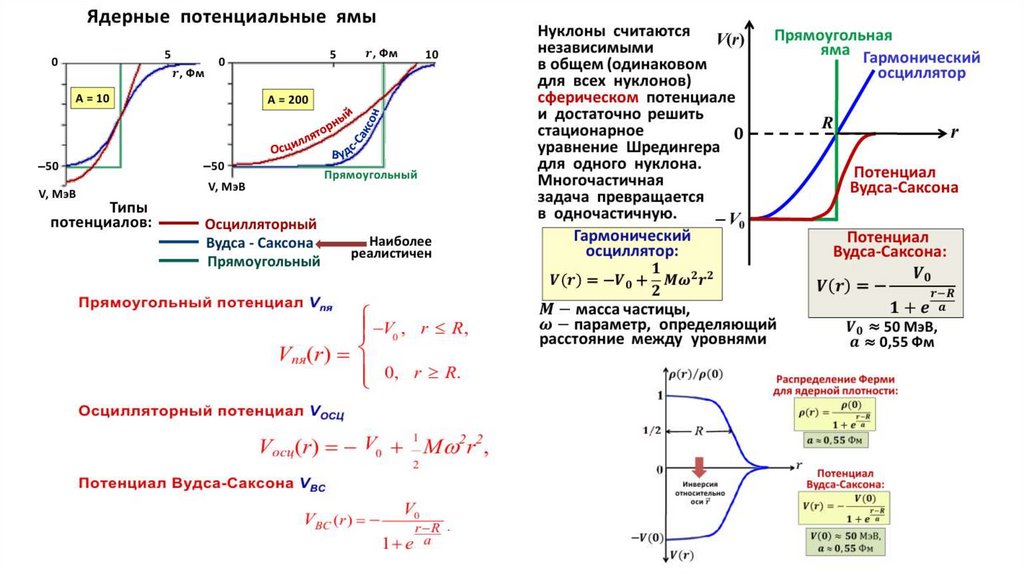
Он должен иметь вид сферически симметричной ямы, а из-за малости радиуса действия ядерных сил должен
меняться с расстоянием аналогично тому, как меняется плотность ядерной материи.
В связи с этим наиболее близким к реальному потенциалу для нейтронов оказывается потенциал
Вудса-Саксона
U0
U r
1 exp r R a
U0 – глубина потенциальной ямы (около 50 МэВ),
R – радиус ядра, определяемый формулой (2.3),
а – размер области, в которой происходит наиболее сильное изменение UССП (0,6-0,7 фм)
40.
Для протонов к потенциалу необходимо добавить самосогласованный кулоновскийпотенциал. Его выбирают в виде энергии взаимодействия точечного элементарного
заряда и равномерно заряженного шара с радиусом R и зарядом (Z–1)е.
Решение уравнения Шредингера с потенциалом Вудса-Саксона
U r
2 r 2
2
2 x 2 y 2 z 2
2
U x U y U z
Частицу в таком поле можно рассматривать как трехмерный гармонический
осциллятор с частотой колебаний ω
41.
42.
Квантовый гармонический осцилляторЛинейным, или одномерным гармоническим осциллятором называется частица,
2
2 2
движущаяся в потенциале
kx
x
U x
2
2
такая частица совершает в направлении х гармонические колебания с циклической
частотой
k
d x
E
Уравнение Шредингера для одномерного осциллятора 2 dx2
2
2
введем безразмерные величины энергии и координаты
d
2 2
d
2
Уравнение преобразуется
При ν = 1 решением этого уравнения является функция
Энергия в основном состоянии равна
E0 2
2
2 2
2E
, x
0 exp
2
2
43.
В этом случае переменные в уравнении Шредингера разделяются, и задача сводится ктрем независимым линейным осцилляторам.
В результате энергия частицы принимает значения
3
E nx , n y , nz nx n y nz
2
(в единицах ħω) 3/2, 5/2, 7/2 и т.д
эквидистантные уровни теперь вырождены - одной и той же энергии Е соответствует
g(Е) различных комбинаций квантовых чисел
При переходе из декартовой системы координат в сферическую имеем для волновых
функций
x, y, z x x y y z z
r, , r r
44.
Из теории строения атома известно, что в этом случае решениеуравнения Шредингера предполагает зависимость энергии также от
трех квантовых чисел, называемых
радиальным (n),
орбитальным (l) и
магнитным (ml).
Два последних определяют момент импульса частицы L и его
проекцию L на ось z
45.
• Так как в центральном поле нет выделенных направлений, каждоесостояние с заданными n и l (2l + 1)-кратно вырождено по ml.
• Значения l в квантовой физике принято записывать символически, в виде
букв латинского алфавита:
l
0
1
2
3
4
5
6
7
символ
s
p
d
f
g
h
I
j
• Комбинацию квантовых чисел n и l в этом случае обозначают так: (n+1)l.
(число n + 1 называют главным квантовым числом). Например,
состояние {n, l} = {0, 2} записывается как 1d.
46.
• Основное состояние сферического гармонического осциллятора – этоневырожденное 1s-состояние,
• первое возбужденное – трижды вырожденное 1p-состояние.
• Для второго возбужденного состояния, которое вырождено
шестикратно, получаем набор из 1d- и 2s-состояний, причем первое
вырождено пятикратно.
• Рассуждая далее аналогичным образом и учитывая всякий раз, что
энергия уровня должна увеличиваться с ростом n и l, можно показать,
что для уровней энергии в сферической осцилляторной яме
3
E n, l 2n l
2
47.
48.
Уровни энергиитрехмерного
гармонического
осциллятора
E/ħω
nx ny nz*
Число перестановок
n l
Символ
2l+1
g(Е)
3/2
5/2
7/2
000
100
110
200
111
210
300
1
3
3
3
1
6
3
0 0
0 1
0 2
1 0
0 3
1 1
1s
1p
1d
2s
1f
2p
1
3
5
1
7
3
1
3
6
11/2
211
220
310
400
3
3
6
3
0 4
1 2
2 0
1g
2d
3s
9
5
1
15
13/2
221
320
311
410
500
3
6
3
6
3
0 5
1 3
2 1
1h
2f
3p
11
7
3
21
15/2
222
321
330
411
420
510
600
1
6
3
3
6
6
3
0 6
1 4
2 2
3 0
1i
2g
3d
4s
13
9
5
1
28
9/2
10
49.
50.
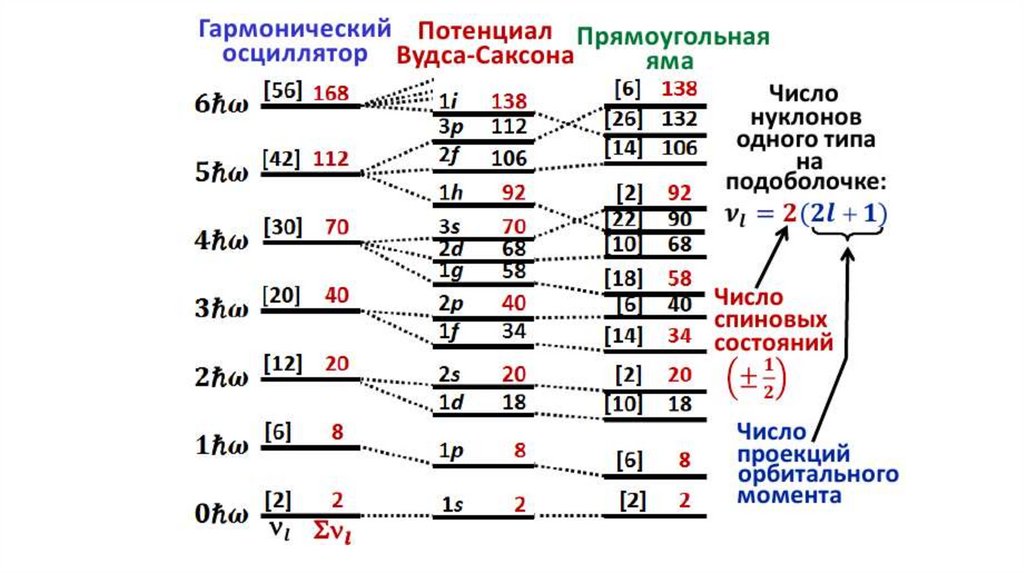
• Заполнение нуклонных оболочек – одночастичных уровней с одинаковойэнергией – должно происходить в соответствии с принципом Паули.
• При этом в основном состоянии будут заняты только самые нижние
уровни.
• Протонные и нейтронные оболочки заселяются независимо.
• Максимальное число нуклонов одного типа на уровне с фиксированной
энергией равно
E 2 g E
где множитель 2 – это число возможных ориентаций спина нуклона S. Тогда
числа ν3/2, ν3/2 + ν5/2, ν3/2 + ν5/2 + ν7/2 и т.д. должны совпадать с магическими
числами.
Однако, как показывает простой подсчет (см. табл. 3.1), совпадают лишь
первые три числа (2, 8 и 20)
51.
Спин-орбитальное взаимодействиеМ. Гёпперт-Майер и Дж. Йенсен показали, что силы, действующие на нуклон со
стороны всех остальных, зависят не только от его координат, но и от взаимной
ориентации спина S и орбитального момента L - спин-орбитальное взаимодействие
L r p r m v
к потенциалу самосогласованного поля необходимо добавить потенциал спинорбитального взаимодействия
U sl 2 f r S L
Спин-орбитальное взаимодействие приводит к тому, что ни орбитальный момент, ни
спин больше не являются (даже приблизительно) сохраняющимися величинами.
Сохраняется лишь полный момент количества движения
J L S
и соответствующее ему квантовое число j. Так как
2 S L J 2 L2 S 2
52.
при заданных числах j и l2 S L j j 1 l l 1 3 / 4
2
C учетом того, что j = l ± ½, добавка к энергии уровня, обусловленная спинорбитальным взаимодействием
l ,
E sl
l 1 ,
–2/3
Обычно α = 24·А
(МэВ)
j l 1/ 2
j l 1/ 2
f r
2
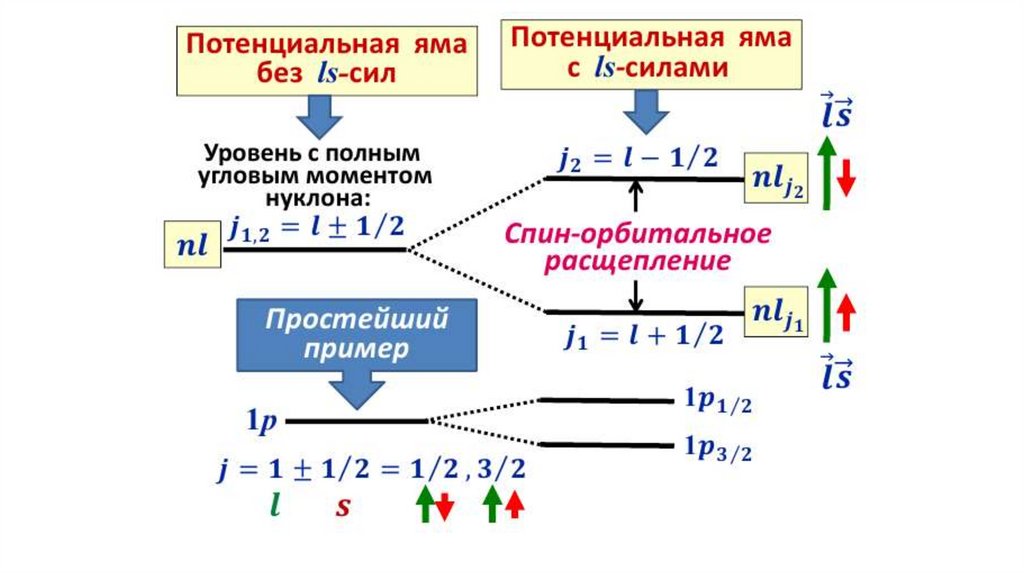
благодаря спин-орбитальному взаимодействию уровень энергии с определенным
значением орбитального квантового числа l (за исключением l = 0) расщепляется на
два.
Величина расщепления равна α(2l + 1).
Уровень с большим значением полного момента, т.е. с j = l + ½, лежит ниже, чем
уровень с j = l – ½
(т.е. нуклон притягивается к ядру сильнее, когда его спин направлен в ту же
сторону, что и орбитальный момент)
53.
54.
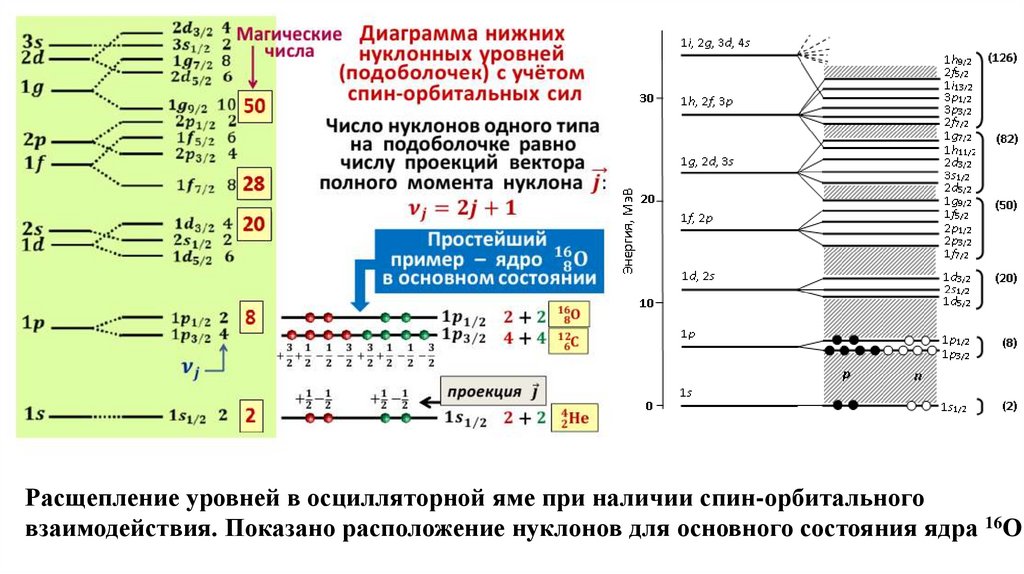
Расщепление уровней в осцилляторной яме при наличии спин-орбитальноговзаимодействия. Показано расположение нуклонов для основного состояния ядра 16О
55.
56.
• Кулоновское отталкивание протонов увеличивает энергию одночастичныхпротонных уровней по сравнению с нейтронными и видоизменяет
потенциальную яму для протонов: она мельче нейтронной и за пределами
ядра должна быть дополнена кулоновским потенциалом.
• При Z и N > 50 последовательности уровней (а значит, и порядок их
заполнения) для протонов и нейтронов различаются: для нейтронов
имеется тенденция к заполнению сначала уровней с меньшими
моментами.
• По этой же причине наиболее вероятным значением магического числа для
протонной оболочки считают Z = 114.
57.
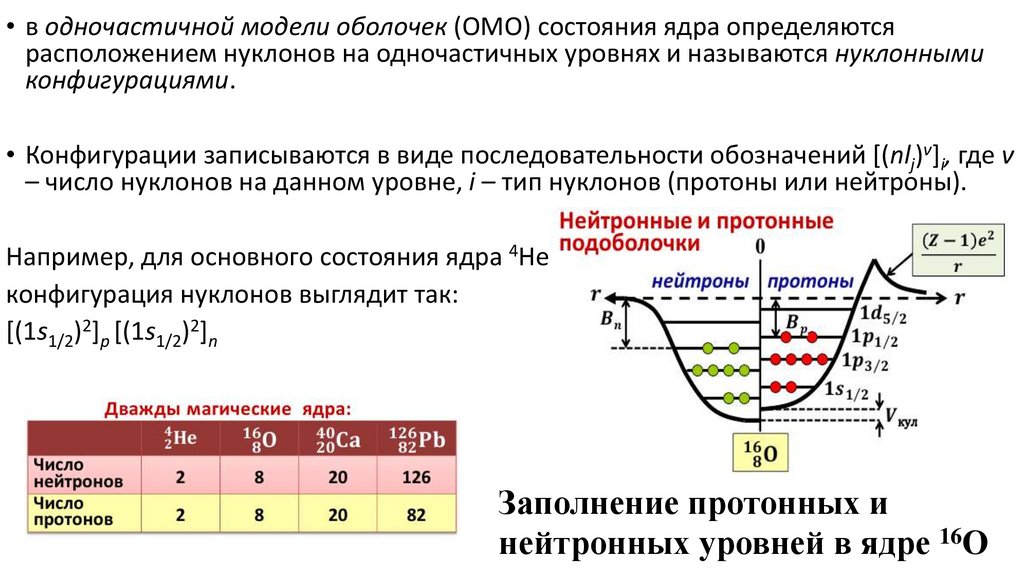
• в одночастичной модели оболочек (ОМО) состояния ядра определяютсярасположением нуклонов на одночастичных уровнях и называются нуклонными
конфигурациями.
• Конфигурации записываются в виде последовательности обозначений [(nlj)ν]i, где ν
– число нуклонов на данном уровне, i – тип нуклонов (протоны или нейтроны).
Например, для основного состояния ядра 4Не
конфигурация нуклонов выглядит так:
[(1s1/2)2]p [(1s1/2)2]n
Заполнение протонных и
нейтронных уровней в ядре 16О










































 Физика
Физика








