Элементы теории атомного ядра

1. Элементы теории атомного ядра

Теоретические модели

2.

Атомное ядро – система взаимодействующих
нуклонов.
Нуклоны двух типов - протоны и нейтроны.
Все физические свойства атомного ядра
обусловлены его составом и законами
межнуклонного взаимодействия.

3.

Протон имеет электрический заряд и является
источником электрического поля. Так как
протоны в ядре движутся, то к кулоновскому
полю добавляются релятивистские
слагаемые.
Кроме того, движущиеся протоны создают
магнитное поле, которое действует на
магнитные моменты протонов и нейтронов.

4.

Превалирующим в атомном ядре является
межнуклонное притяжение, которое
обусловлено фундаментальным сильным
взаимодействием.
Законы межнуклонного притяжения до сих пор
точно не установлены. Информация об этих
законах получается
1) изучением свойств нуклонных (в первую
очередь двухнуклонных) систем;
2) анализом результатов рассеяния нуклонов
на ядрах.

5.

Эмпирические свойства ядерных (межнуклонных) сил
1. Большая величина (энергия связи дейтрона 2,23 МэВ).
2. Малый радиус действия ( ~ 10 13 см).
3. Независимость от электрического заряда
(изотопическая инвариантность).
4. Зависимость от ориентации спинов.
5. Нецентральный характер.
6. Обменный характер.
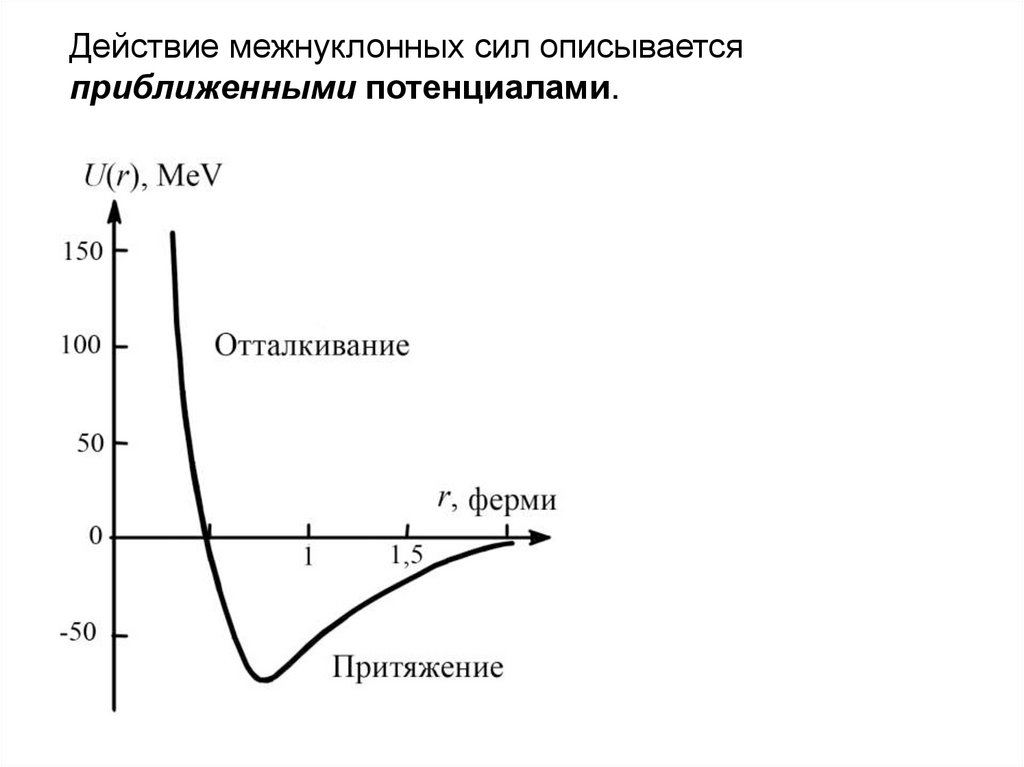
7. Отталкивание на малых расстояниях.
8. Свойство насыщения.
9. Зависимость от скорости.

6.

Сложность физических процессов внутри
атомного ядра не позволяет построить
строгую теорию ядра.
Для описания свойств атомного ядра,
процессов радиоактивности, ядерных реакций
используются различные теоретические
модели, каждая из которых имеет
ограниченную область применения.

7. Капельная модель

Является обоснованием формулы Вайцзеккера.
Капельная модель дает приблизительно правильное
представление о массе и энергии связи ядер, что
позволяет исследовать энергетические условия разных
вариантов распада ядра (в частности, α- и β-распада),
качественно описывает структуру низколежащих уровней
четно-четных ядер, дает возможность построить
полуколичественную теорию деления тяжелых ядер.
Капельная модель не пригодна для количественного
описания энергетических уровней ядер, не позволяет
вычислить характеристики основных и возбужденных
состояний ядер, объяснить периодическое изменение
свойств ядер с изменением массового числа, асимметрию
деления тяжелых ядер и т.д.

8. Формула Вайцзеккера

Есв a1 A a2 A
23
a3 Z A
2
1 3
( A 2Z )
a4
A
2
(1.19)
a1 = 15,75 МэВ; a2 = 17,8 МэВ; a3 = 0,7 МэВ; a4 = 23,7 МэВ
(четно четные ядра)
( нечетно нечетные ядра)
= 12/A1/3 МэВ

9.

Действие межнуклонных сил описывается
приближенными потенциалами.

10.

Одночастичные модели
Вводится самосогласованное поле ядерных сил,
которое действует на один нуклон.
Соответствующие уравнения Шредингера дают
дискретные спектры энергий стационарных состояний
нуклонов в ядре.
Нуклоны являются фермионами, поэтому для них
справедлив принцип Паули.
Протоны и нейтроны обладают независимыми
системами энергетических уровней.

11.

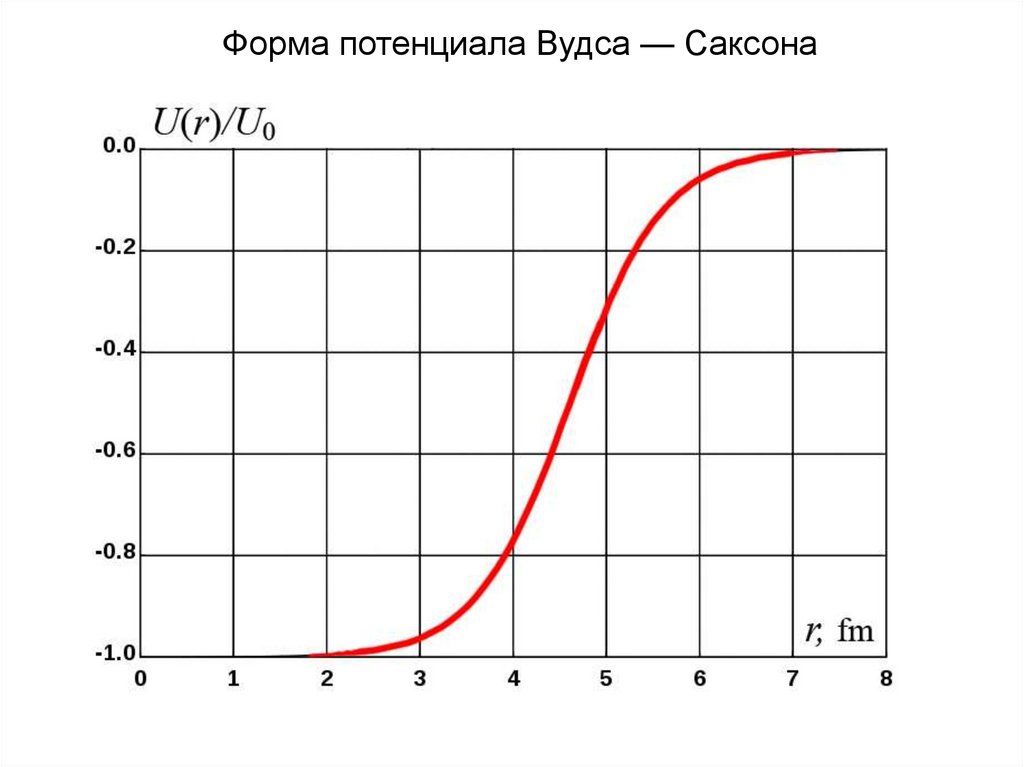
Потенциал Вудса-Саксона
(Пример одночастичной модели)
U0
U (r )
r R
1 exp
a
(4.1)
где R = r0 A1/3 радиус ядра;
r0 ≈ 1,25 фм параметр, приближённо равный
среднему расстоянию между нуклонами в ядре;
A — массовое число ядра;
a ≈ 0,5 фм параметр диффузности, характеризующий
размытие края потенциальной ямы;
U0 ≈ 50 МэВ глубина потенциальной ямы.

12.

Форма потенциала Вудса — Саксона

13.

Потенциал вида (4.1) описывает энергию нейтрона в
ядре.
Для протонов к потенциалу (4.1) добавляется слагаемое,
учитывающее электрическое взаимодействие.
Например:
( Z 1) e 2
R
U e (r )
( Z 1) e 2
R
3 1 r 2
, r R
2 2 R
(4.2)
, r R

14.

Близкие энергетические уровни
нуклонов (как протонов, так и нейтронов)
образуют ядерные оболочки.
Ядра с заполненными оболочками
имеют особенные значения физических
характеристик (спинов, магнитных
моментов, энергий связи, … ) и
обладают особенностями
радиоактивных процессов.
Качественная схема
энергетических уровней
нуклонов
Е

15.

Для согласия с результатами экспериментов к
центрально-симметричному потенциалу требуется
добавить спин-орбитальное слагаемое
V(r) s l
(4.3)
где s – спин нуклона, l – его орбитальный момент.
На следующих слайдах приведены результаты расчёта энергий
одночастичных нуклонных состояний по теоретическим моделям

16.

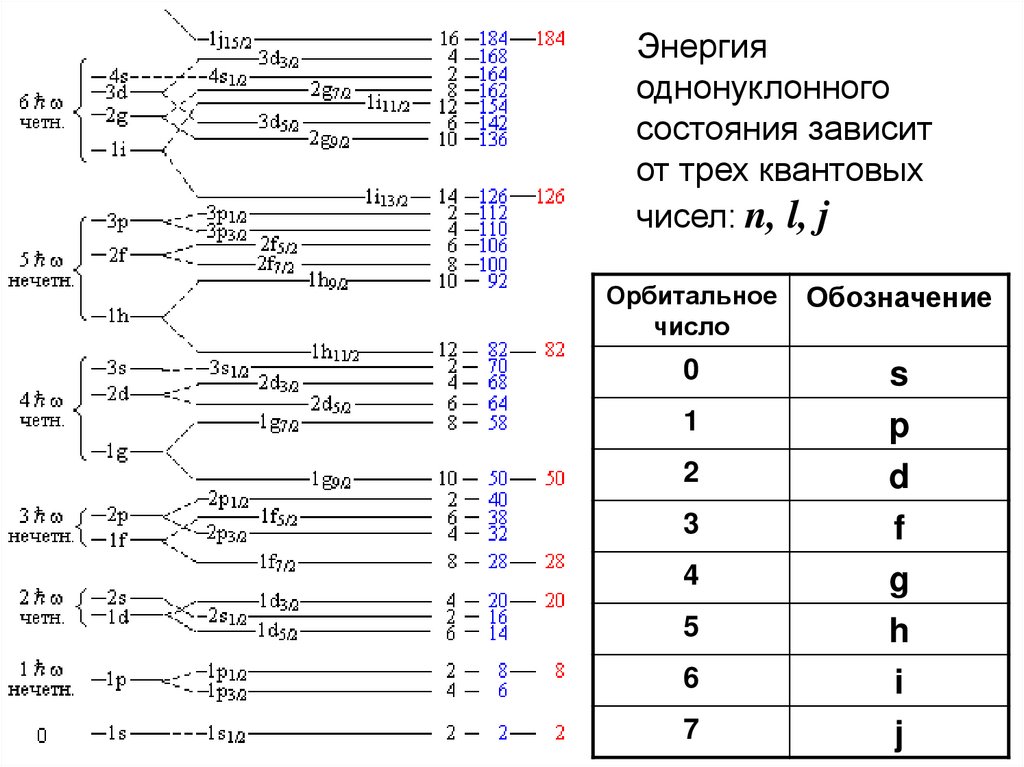
Энергия
однонуклонного
состояния зависит
от трех квантовых
чисел: n, l, j
Орбитальное
число
Обозначение
0
s
1
p
2
d
f
g
3
4
5
6
7
h
i
j

17.

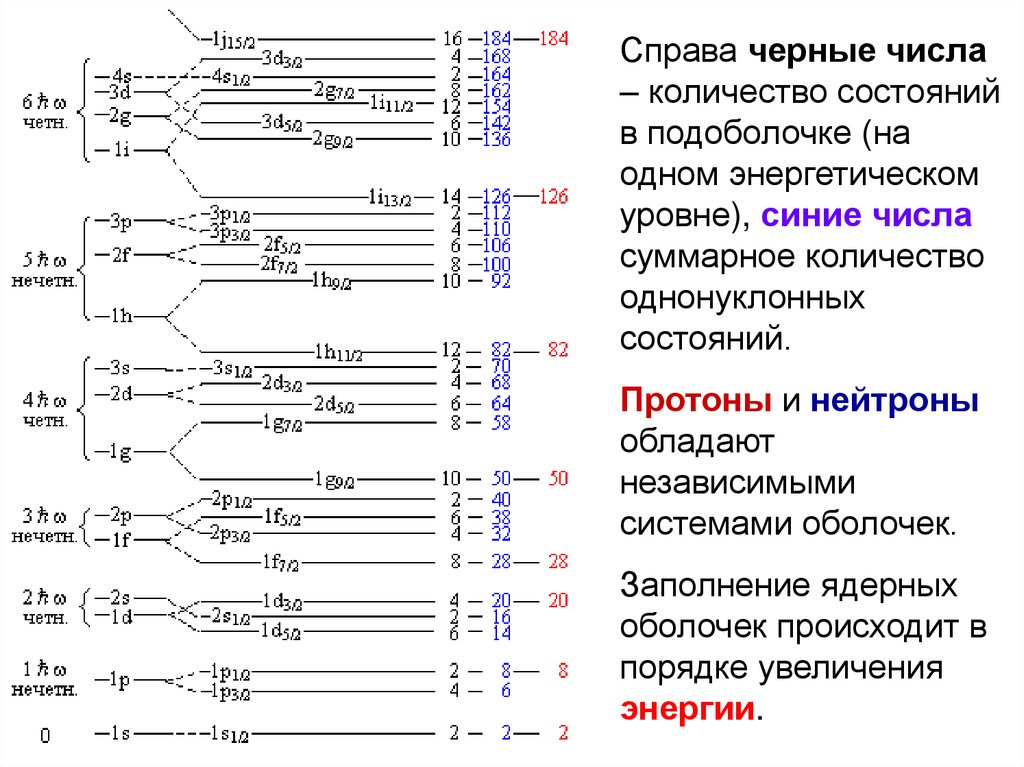
Справа черные числа
– количество состояний
в подоболочке (на
одном энергетическом
уровне), синие числа
суммарное количество
однонуклонных
состояний.
Протоны и нейтроны
обладают
независимыми
системами оболочек.
Заполнение ядерных
оболочек происходит в
порядке увеличения
энергии.

18.

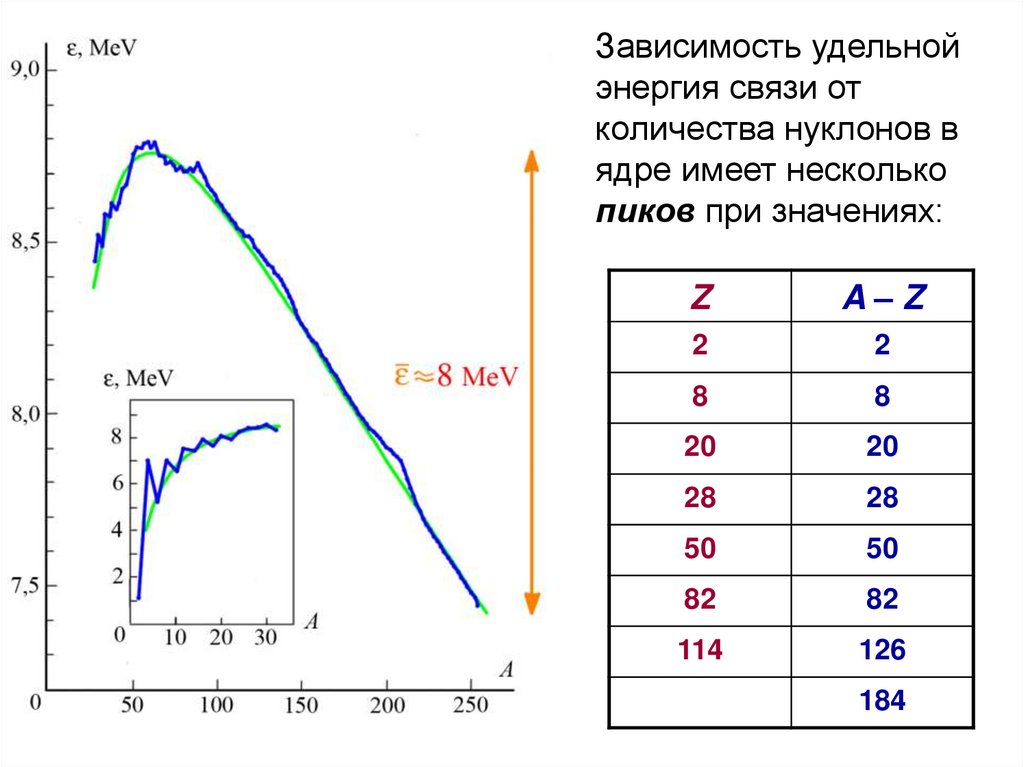
Зависимость удельной
энергия связи от
количества нуклонов в
ядре имеет несколько
пиков при значениях:
Z
A–Z
2
2
8
8
20
20
28
28
50
50
82
82
114
126
184

19.

Заполнение ядерной
оболочки
обусловливает
повышенную
энергию связи ядра.
Красные числа –
магические числа
нейтронов

20.

Основные результаты оболочечной модели
1. Спин основного состояния четно-четного ядра (Z и N четные числа) равен нулю.
2. Спин основных состояний ядер с нечетным числом
нуклонов А равен полному моменту j неспаренного
нуклона.
3. Спин нечетно-нечетных ядер, неспаренные нуклоны
которого находятся в одинаковых состояниях, равен
удвоенному полному моменту неспаренного нуклона.
4. Энергия однонуклонного состояния при фиксированном
главном квантовом числе n растет с ростом
орбитального квантового числа l.
5. Спин-орбитальное взаимодействие для параллельных
спина и орбитального момента нуклона больше, чем для
антипараллельных.

21.

Наилучшие предсказания оболочечная модель дает
для ядер с заполненными оболочками и для ядер,
отличающихся от них на 1 2 нуклона.
Спектр энергий возбужденных
состояний ядра 209Pb.
Z = 82, N = 128+1
На рисунке показаны возбужденные состояния дважды
магического ядра с одним валентным нуклоном 209Pb.
Большинство состояний (кроме состояния 1/2 ) описываются
одночастичной оболочечной моделью.

22.

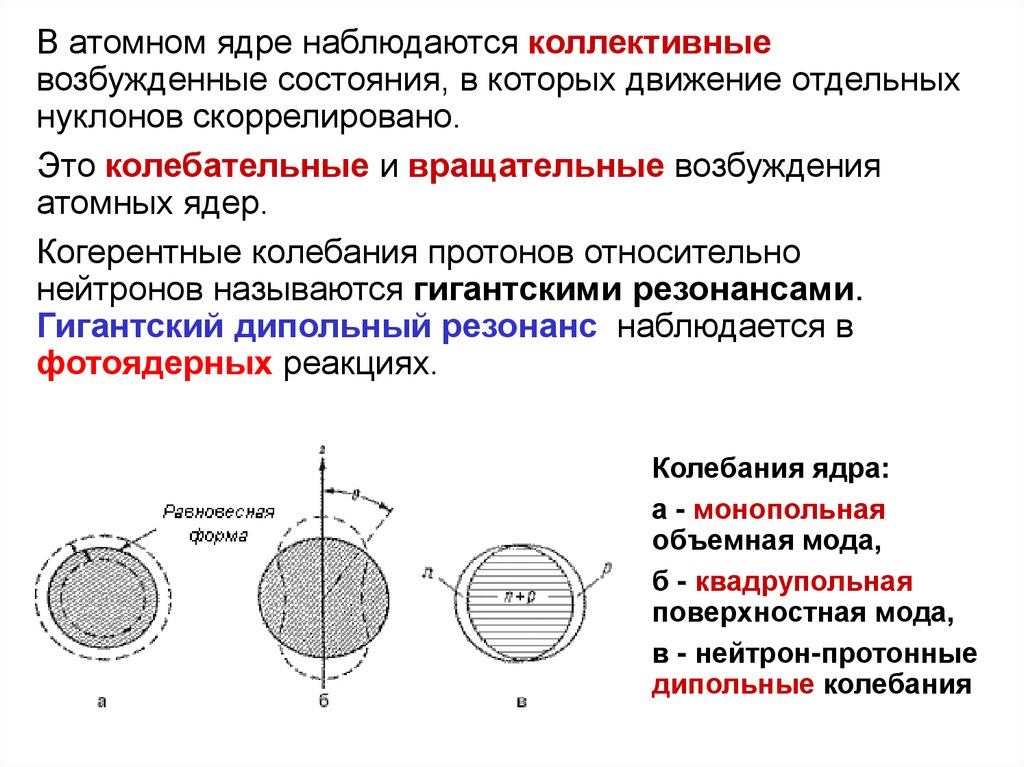
В атомном ядре наблюдаются коллективные
возбужденные состояния, в которых движение отдельных
нуклонов скоррелировано.
Это колебательные и вращательные возбуждения
атомных ядер.
Когерентные колебания протонов относительно
нейтронов называются гигантскими резонансами.
Гигантский дипольный резонанс наблюдается в
фотоядерных реакциях.
Колебания ядра:
а - монопольная
объемная мода,
б - квадрупольная
поверхностная мода,
в - нейтрон-протонные
дипольные колебания

23.

У несферического ядра изменяются одночастичные
уровни, меняется частота колебаний, появляются
вращательные степени свободы.
Энергия вращательных состояний четно-четных
деформированных аксиально-симметричных ядер
описывается выражением
j ( j 1)
E
2I
2
(4.4)
где I - момент инерции ядра, j – спиновое квантовое
число ядра.

24.

Вращательный спектр деформированного ядра 170Hf

25.

Обобщенная модель
Модель, которая позволила бы одновременно учесть как
одночастичные, так и коллективные степени свободы ядра
- обобщенная модель была предложена в начале 50-х гг.
ХХ века Д. Рейнуотером, О. Бором и Б. Моттельсоном.
В этой модели предполагается сильная связь внешних по
отношению к заполненным оболочкам нуклонов с остовом,
что может приводить к устойчивой равновесной
деформации ядра.
Движение остова описывается в гидродинамической
модели.
Одночастичные состояния рассчитываются в
деформированном потенциале.
Первые расчеты одночастичных состояний с
использованием деформированного аксиальносимметричного потенциала были выполнены в 1955 году
C.Нильссоном.

26.

Деформированный потенциал Нильссона:
m 2 2
2
2 2
2
VD x1 x2 3 x3 C1 ( LS ) C2 L
2
где x1, x2 и x3 – координаты нуклона во
внутренней системе координат,
3 – частота колебаний вдоль оси симметрии,
– частота колебаний в перпендикулярном
направлении.
(4.5)

27.

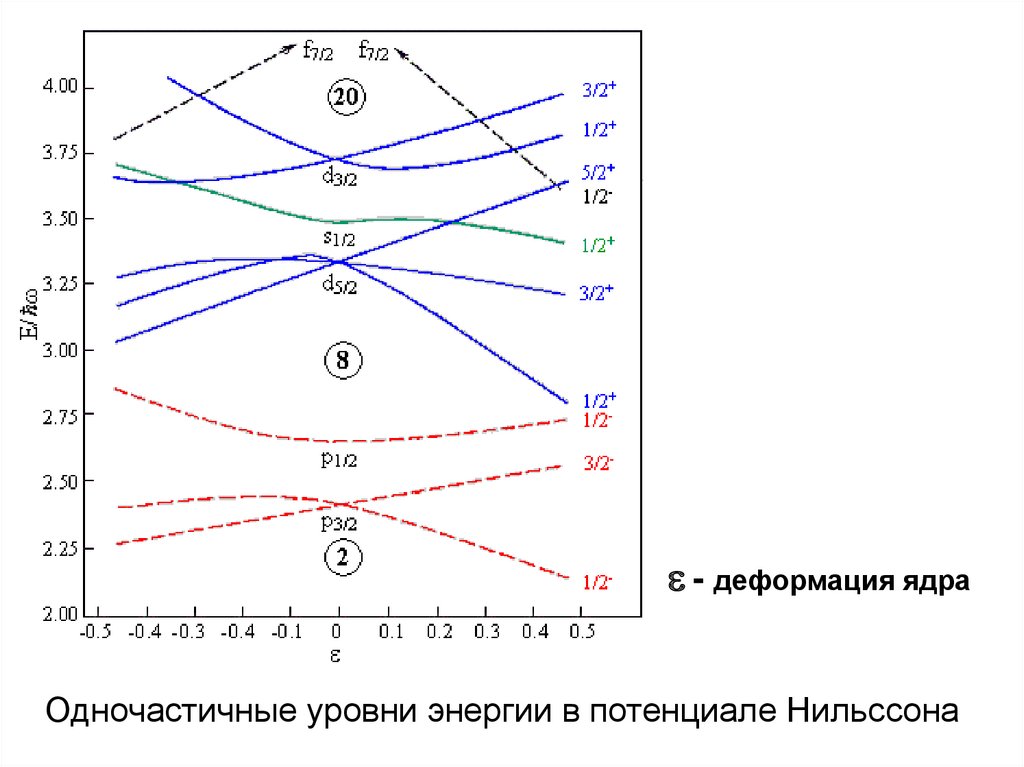
- деформация ядра
Одночастичные уровни энергии в потенциале Нильссона

28.

Общая теория атомного ядра, способная
предсказывать количественные
результаты экспериментов, пока не
разработана из-за ужасающей сложности
физики межнуклонных взаимодействий .
Информация о физических
характеристиках атомных ядер и
ядерных процессах получается, в
основном, в экспериментах.