Действия над векторами в пространстве

1. Действия над Векторами в пространстве

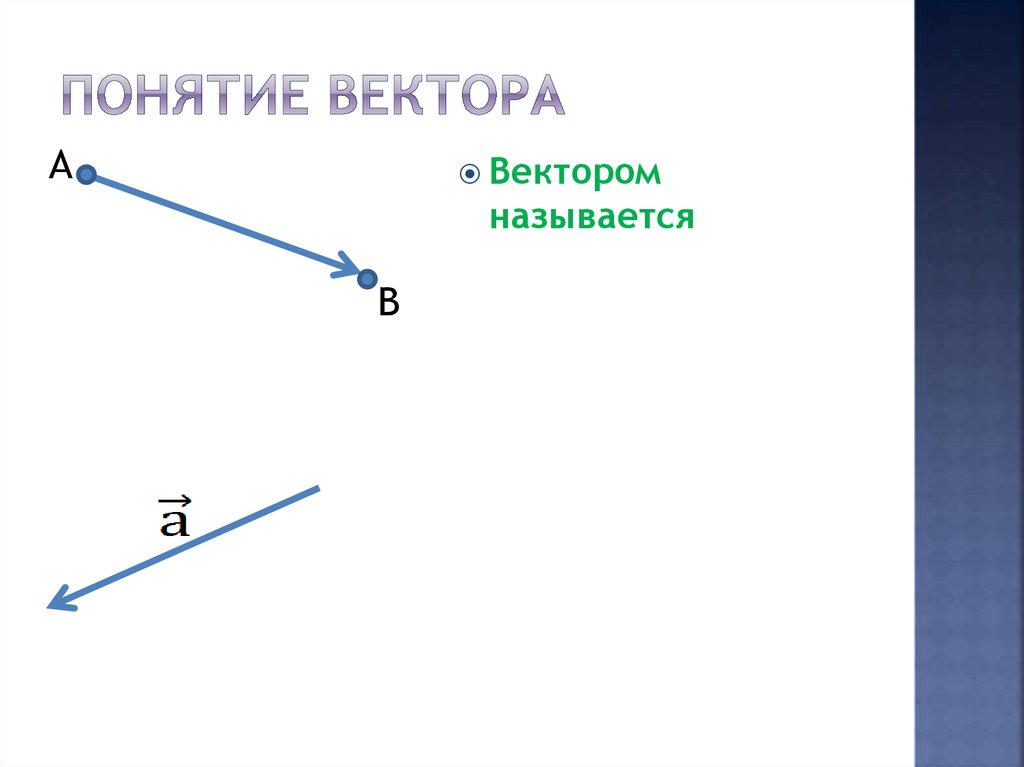
2. Понятие вектора

А
Вектором
В
называется
направленный
отрезок
А – начало вектора
В – конец вектора
- Обозначение:
АВ

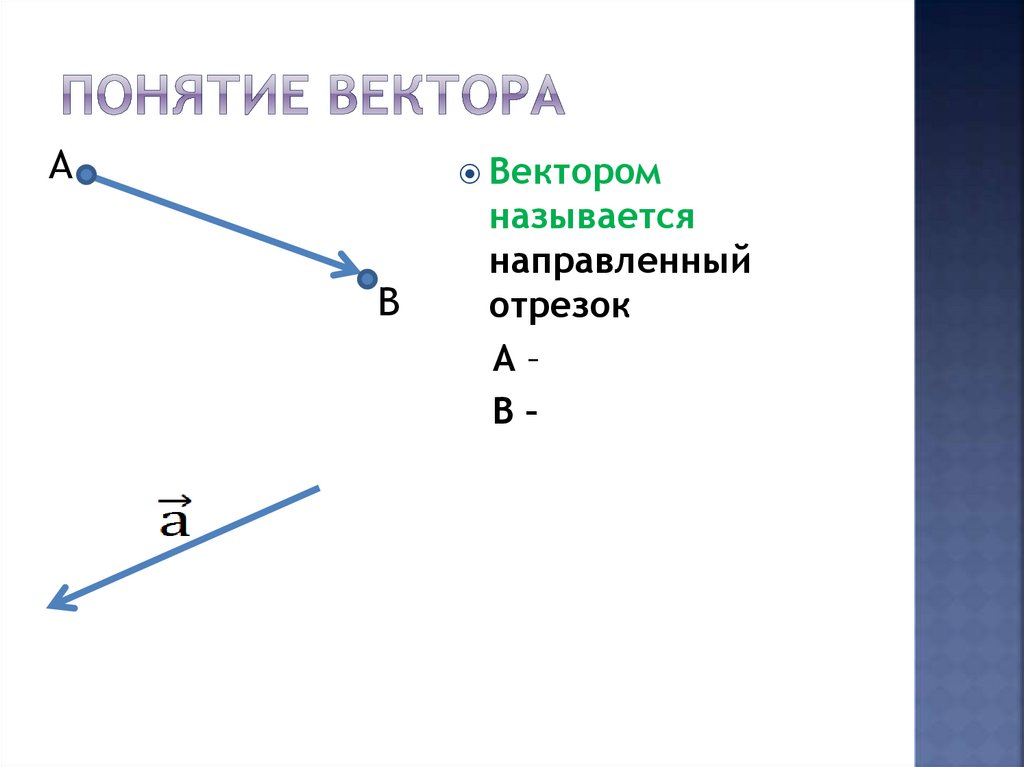
3. Понятие вектора

А
Вектором
В
называется
направленный
отрезок
А – начало вектора
В – конец вектора
- Обозначение:
АВ

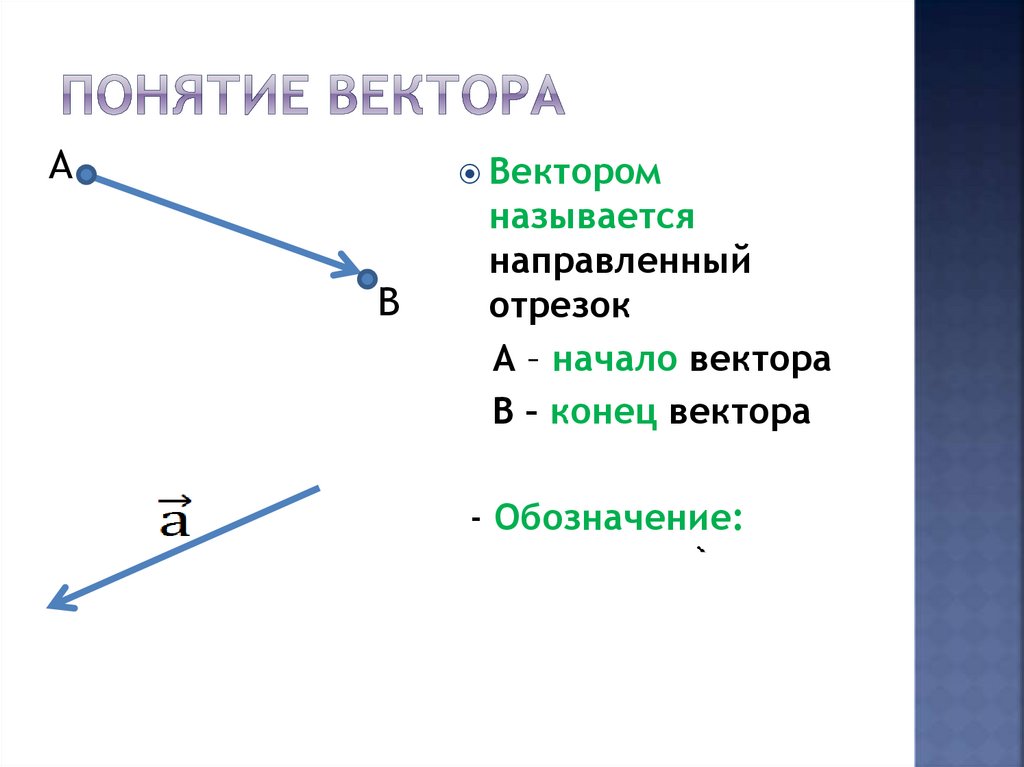
4. Понятие вектора

А
Вектором
В
называется
направленный
отрезок
А – начало вектора
В – конец вектора
- Обозначение:
АВ

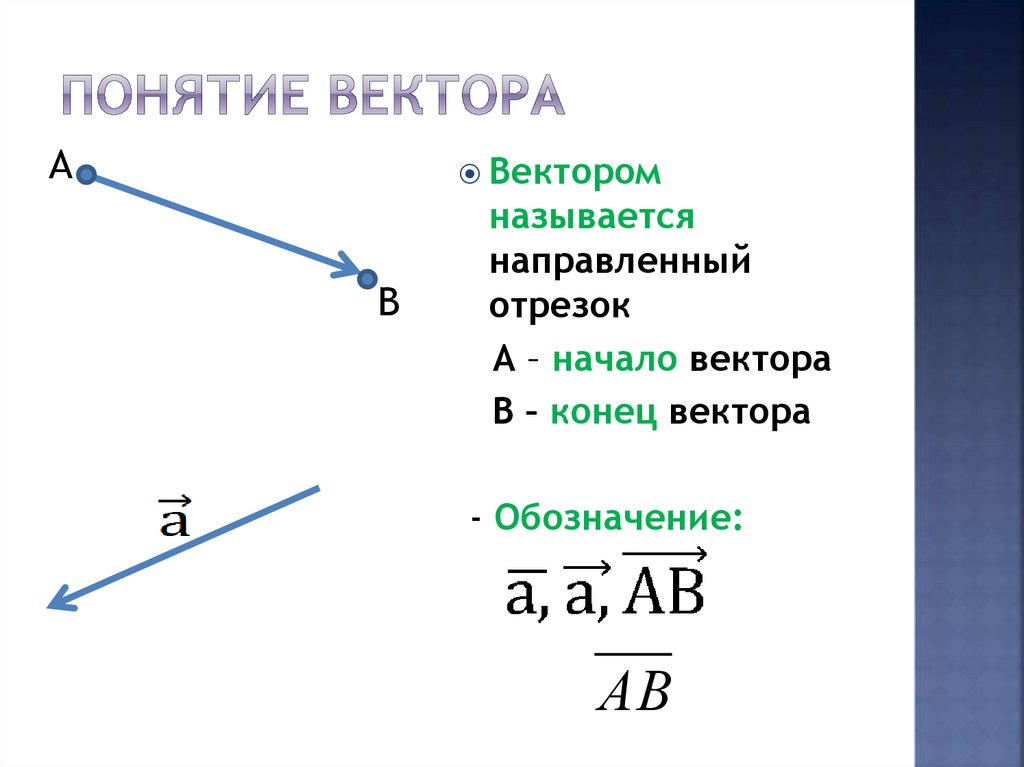
5. Понятие вектора

А
Вектором
В
называется
направленный
отрезок
А – начало вектора
В – конец вектора
- Обозначение:
АВ

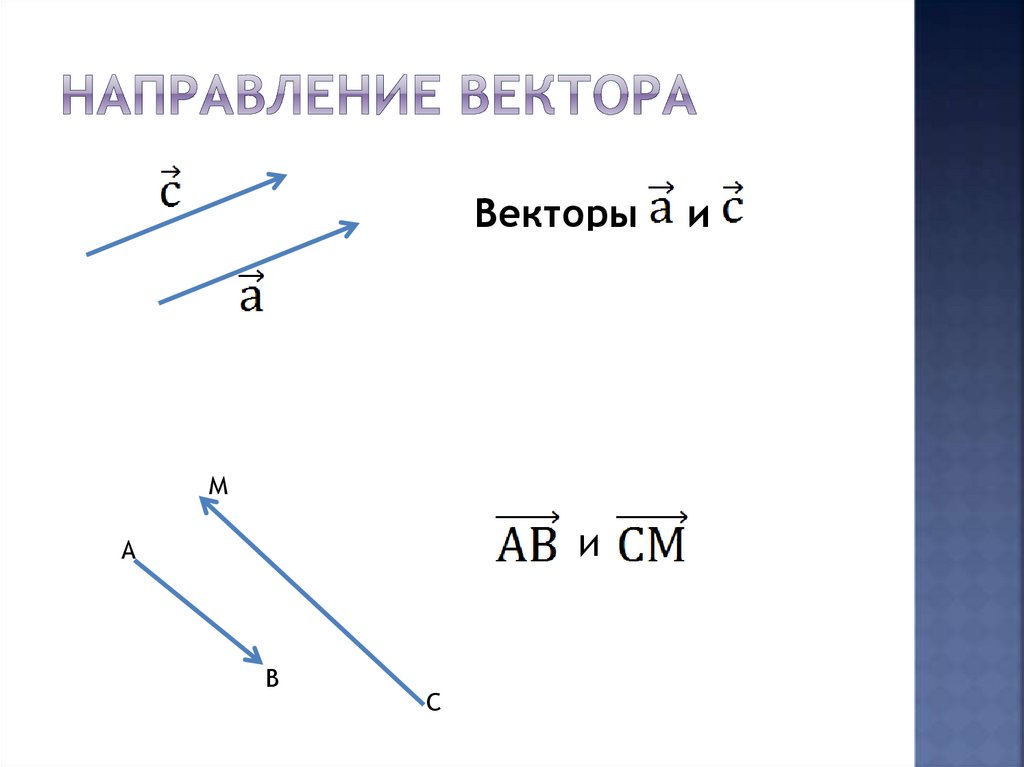
6. Направление вектора

Векторы
и
одинаково
направлены
М
и
А
противоположно
направлены
В
С

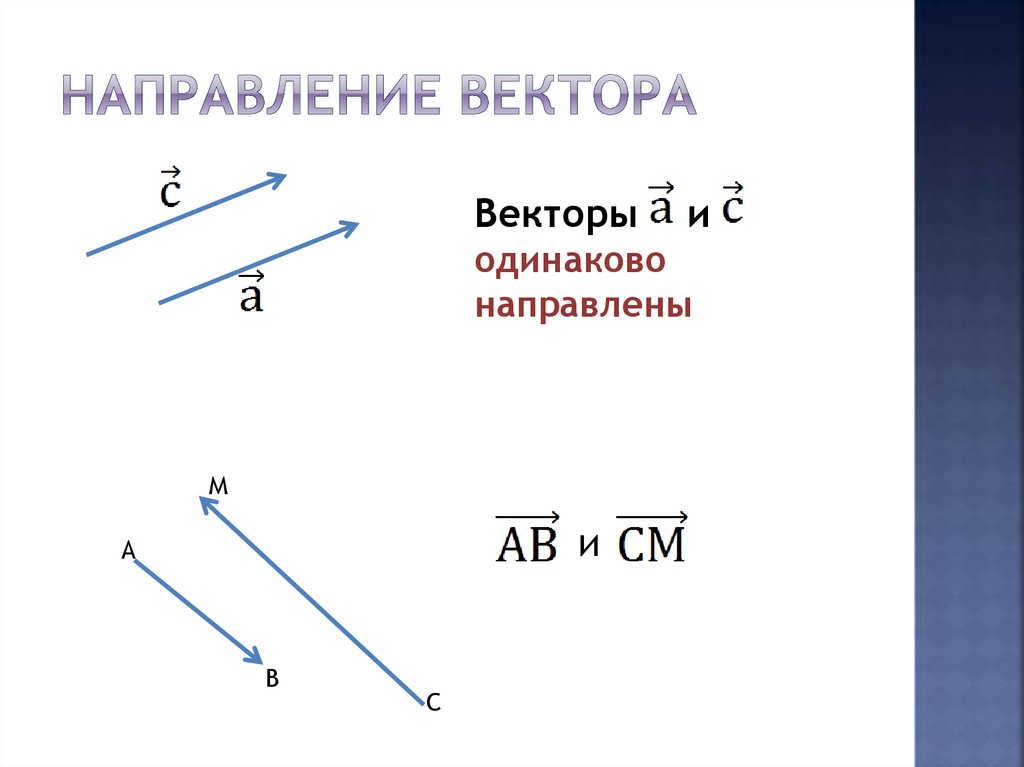
7. Направление вектора

Векторы
и
одинаково
направлены
М
и
А
противоположно
направлены
В
С

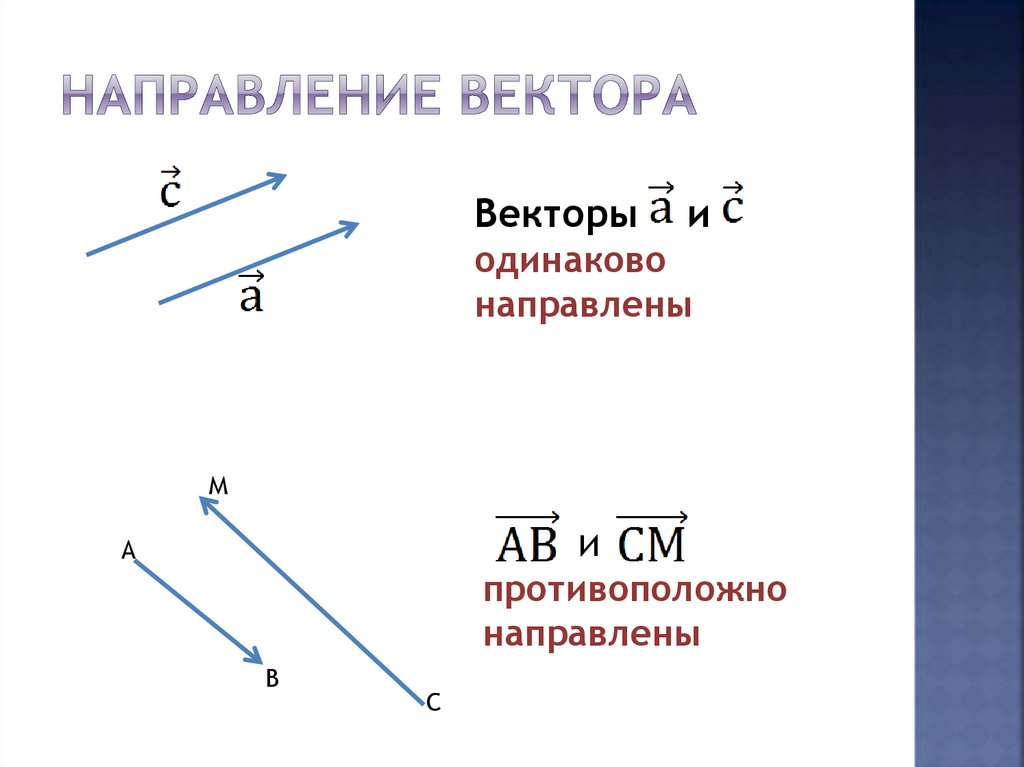
8. Направление вектора

Векторы
и
одинаково
направлены
М
и
А
противоположно
направлены
В
С

9. Абсолютная величина вектора

Абсолютная величина
(или модуль) вектора
– длина отрезка,
изображающего
вектор
Обозначение:
Нулевой вектор – вектор,
у которого начало
совпадает с его концом

10. Абсолютная величина вектора

Абсолютная величина
(или модуль) вектора
– длина отрезка,
изображающего
вектор
Обозначение:
Нулевой вектор – вектор,
у которого начало
совпадает с его концом

11. Абсолютная величина вектора

Абсолютная величина
(или модуль) вектора
– длина отрезка,
изображающего
вектор
Обозначение:
Нулевой вектор – вектор,
у которого начало
совпадает с его концом

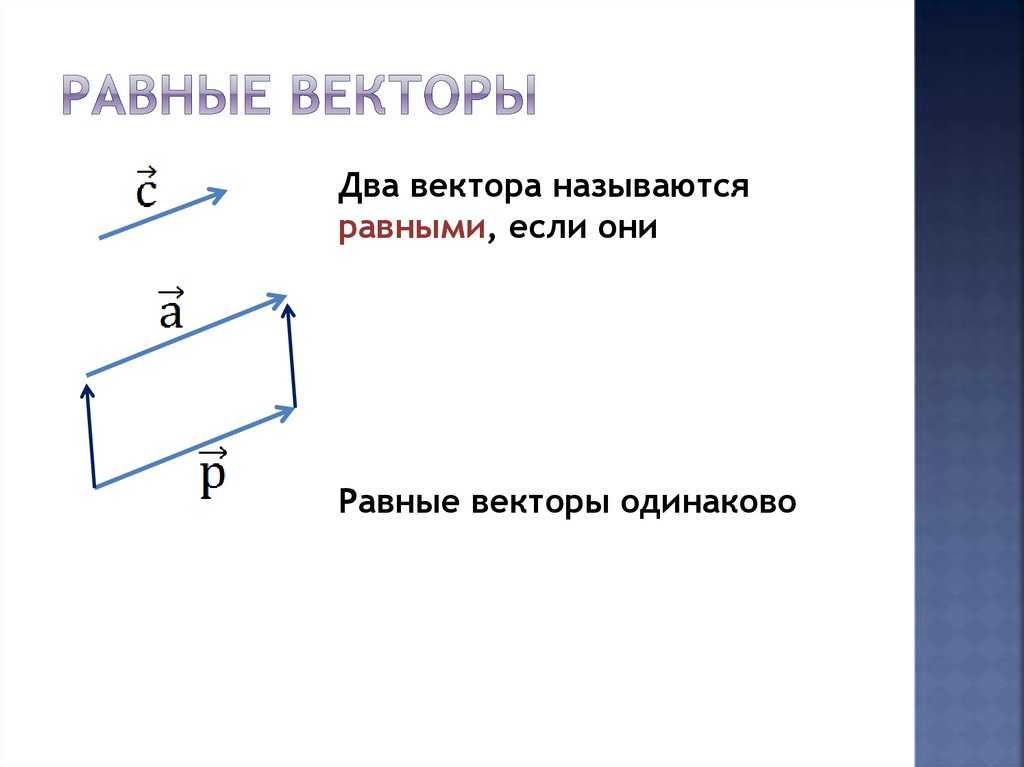
12. Равные векторы

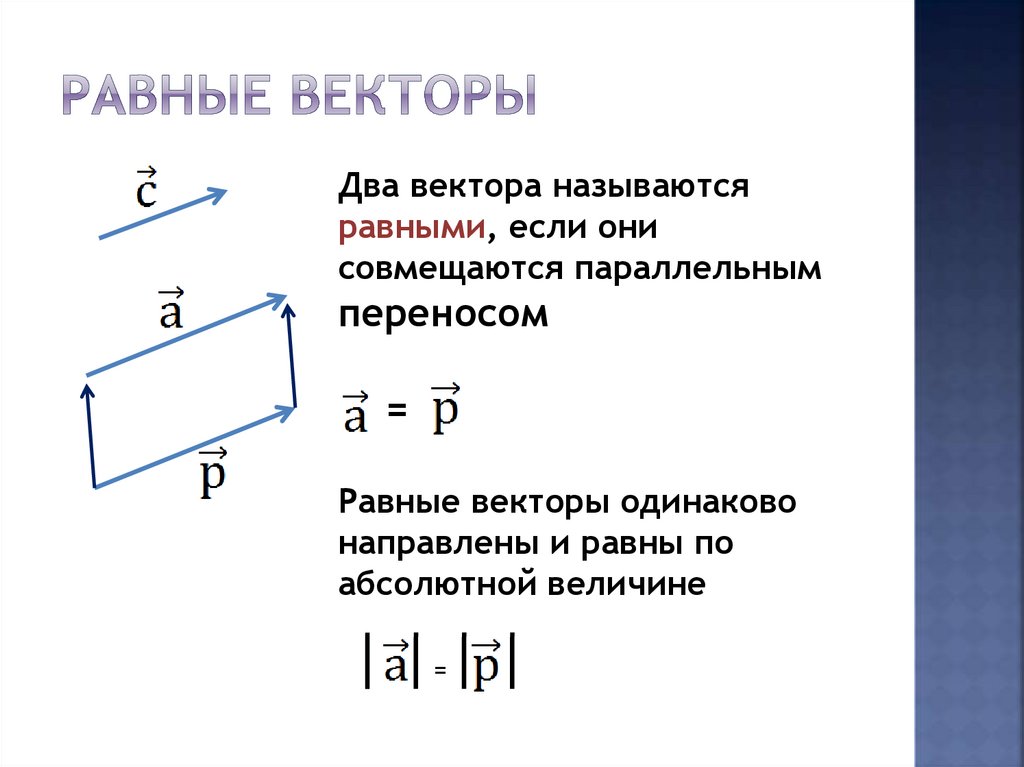
Два вектора называются
равными, если они
совмещаются параллельным
переносом
=
Равные векторы одинаково
направлены и равны по
абсолютной величине
=

13. Равные векторы

Два вектора называются
равными, если они
совмещаются параллельным
переносом
=
Равные векторы одинаково
направлены и равны по
абсолютной величине
=

14. Равные векторы

Два вектора называются
равными, если они
совмещаются параллельным
переносом
=
Равные векторы одинаково
направлены и равны по
абсолютной величине
=

15. Коллинеарные векторы

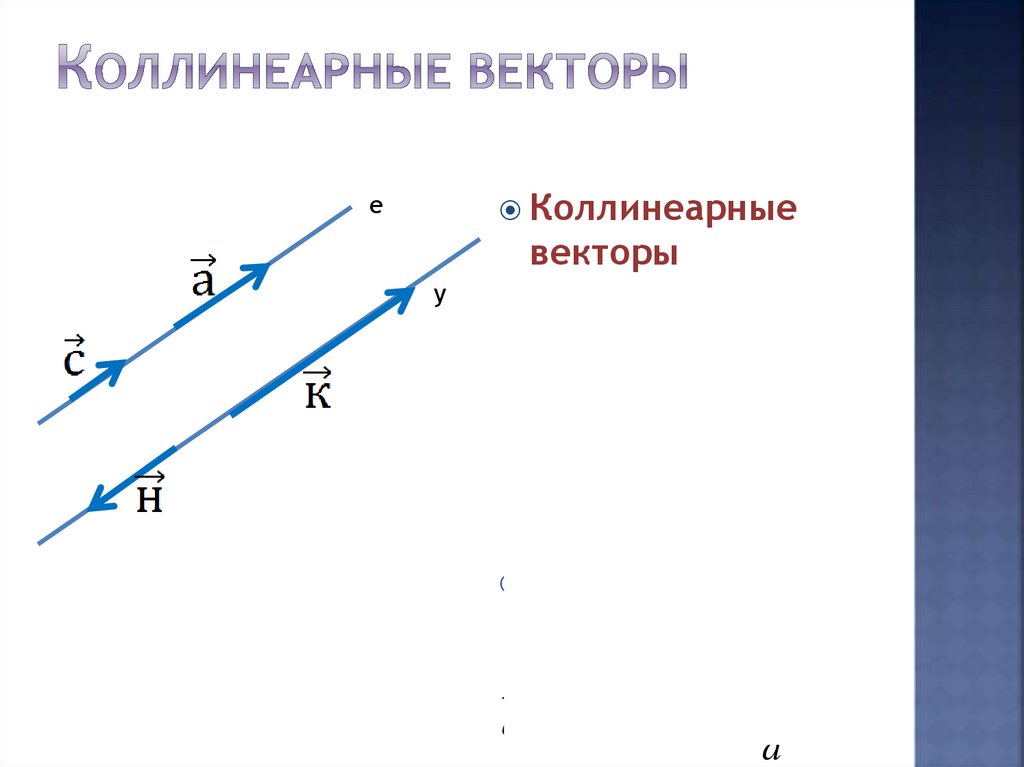
Коллинеарные
е
векторы
сонаправлены и
лежат на
параллельных
прямых или на
одной.
у
, ,
коллинеарные
а k
k
a

16. Коллинеарные векторы

Коллинеарные
е
векторы
сонаправлены и
лежат на
параллельных
прямых или на
одной.
у
, ,
коллинеарные
а k
k
a

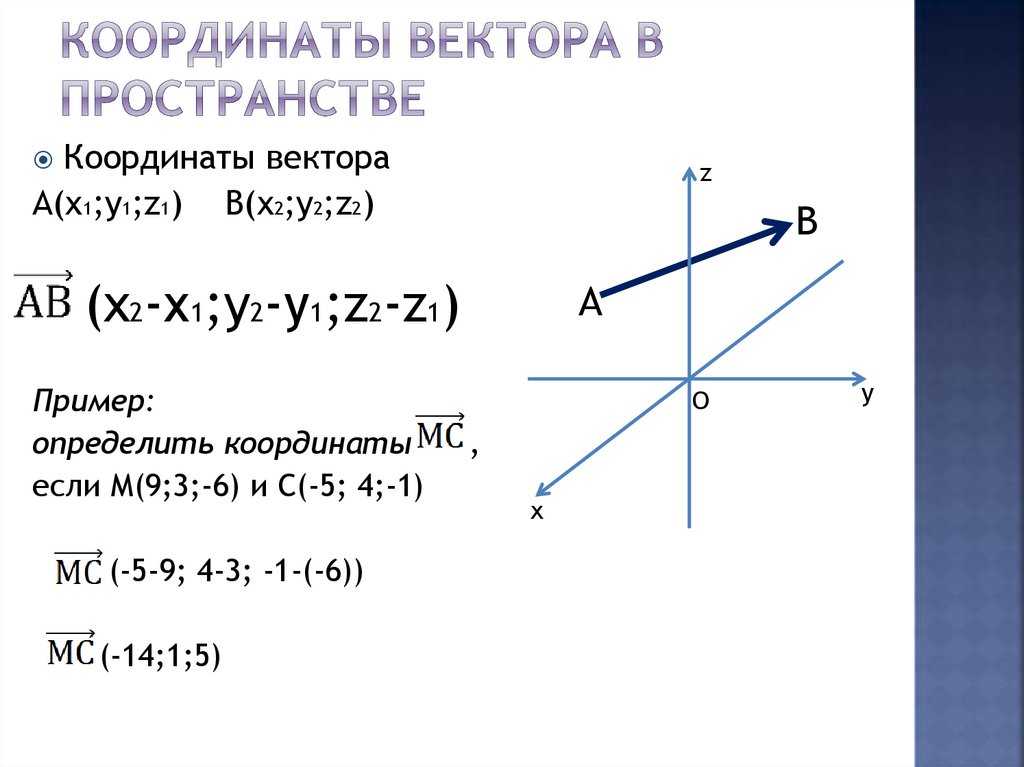
17. Координаты вектора в пространстве

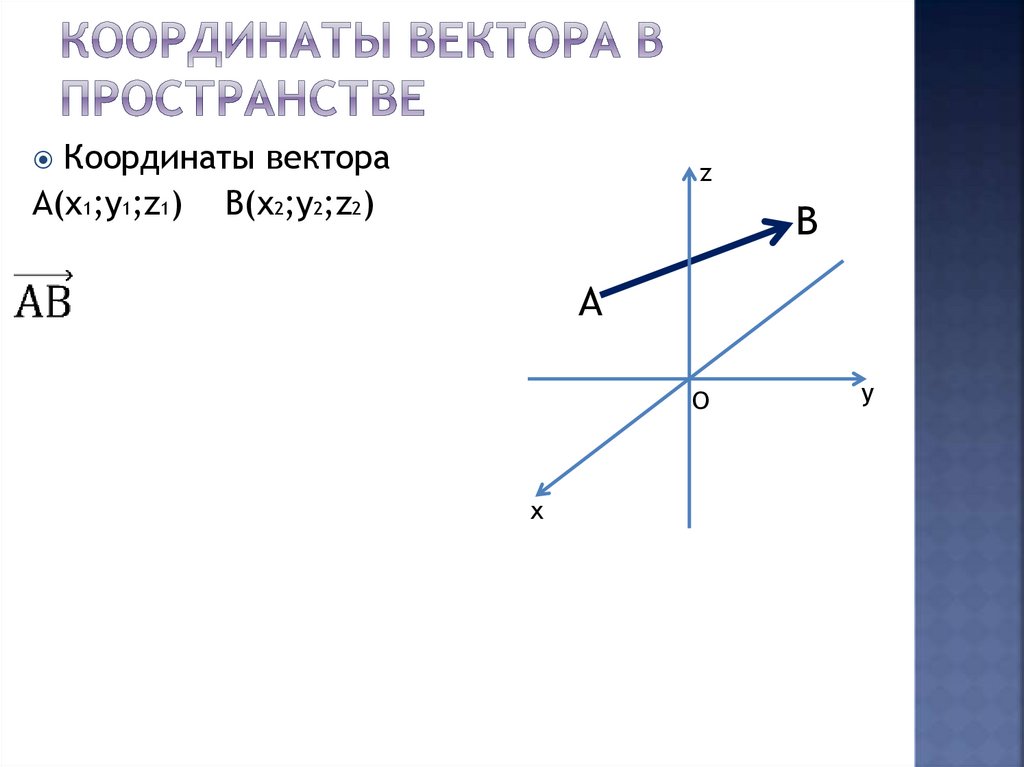
Координаты вектора
А(х1;у1;z1)
z
B(x2;y2;z2)
В
(x2-х1;y2-у1;z2-z1)
Пример:
определить координаты
если М(9;3;-6) и С(-5; 4;-1)
(-5-9; 4-3; -1-(-6))
(-14;1;5)
А
O
,
x
y

18. Координаты вектора в пространстве

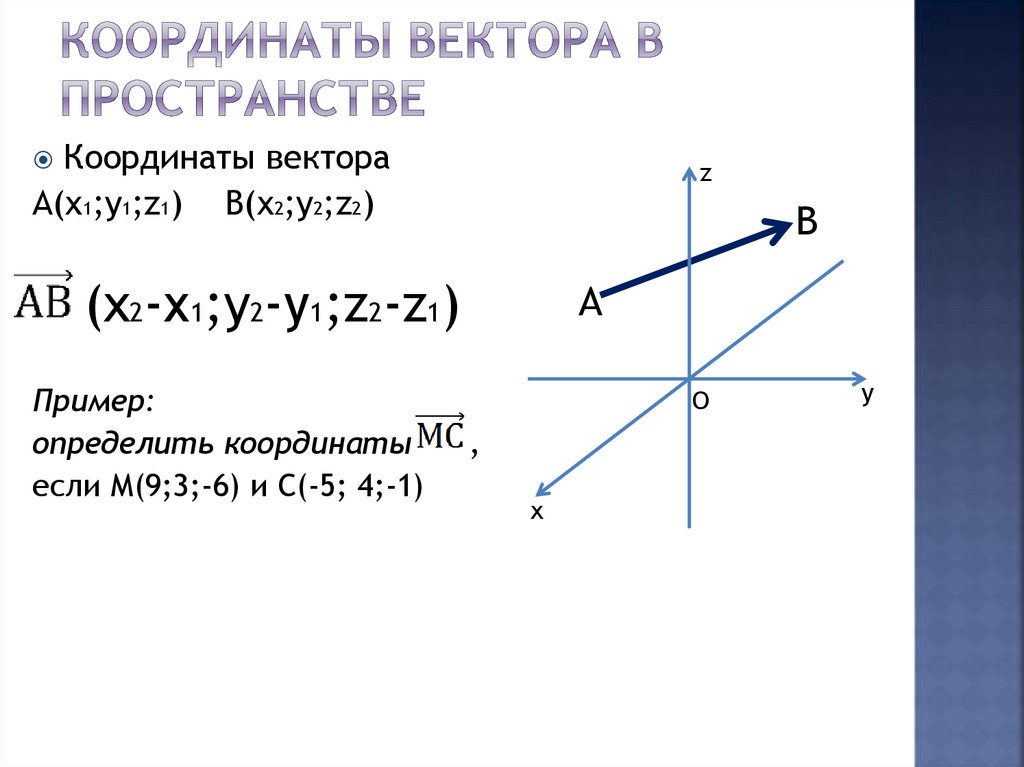
Координаты вектора
А(х1;у1;z1)
z
B(x2;y2;z2)
В
(x2-х1;y2-у1;z2-z1)
Пример:
определить координаты
если М(9;3;-6) и С(-5; 4;-1)
(-5-9; 4-3; -1-(-6))
(-14;1;5)
А
O
,
x
y

19. Координаты вектора в пространстве

Координаты вектора
А(х1;у1;z1)
z
B(x2;y2;z2)
В
(x2-х1;y2-у1;z2-z1)
Пример:
определить координаты
если М(9;3;-6) и С(-5; 4;-1)
(-5-9; 4-3; -1-(-6))
(-14;1;5)
А
O
,
x
y

20. Равные векторы

Определение равных векторов:
Векторы называются
z
равными, если они
имеют равные
соответствующие
координаты и
абсолютные величины.
(х;y;z)
(a;b;c)
Если х=а,у=b, z=с, то
=
В
А
O
x С
М
y

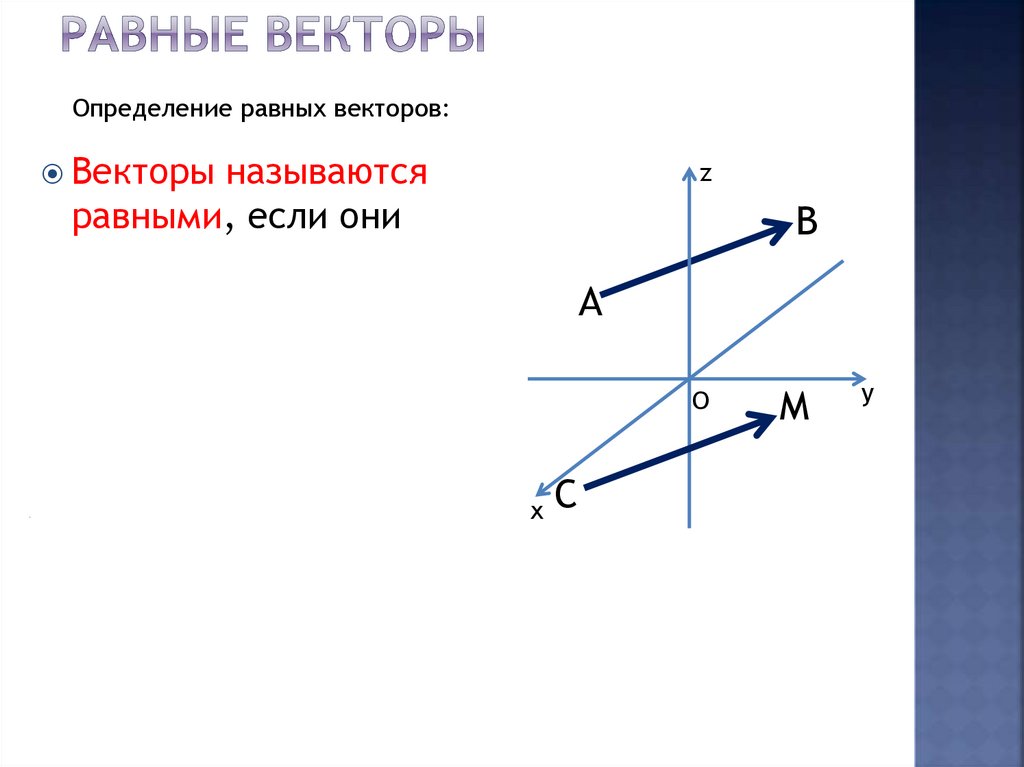
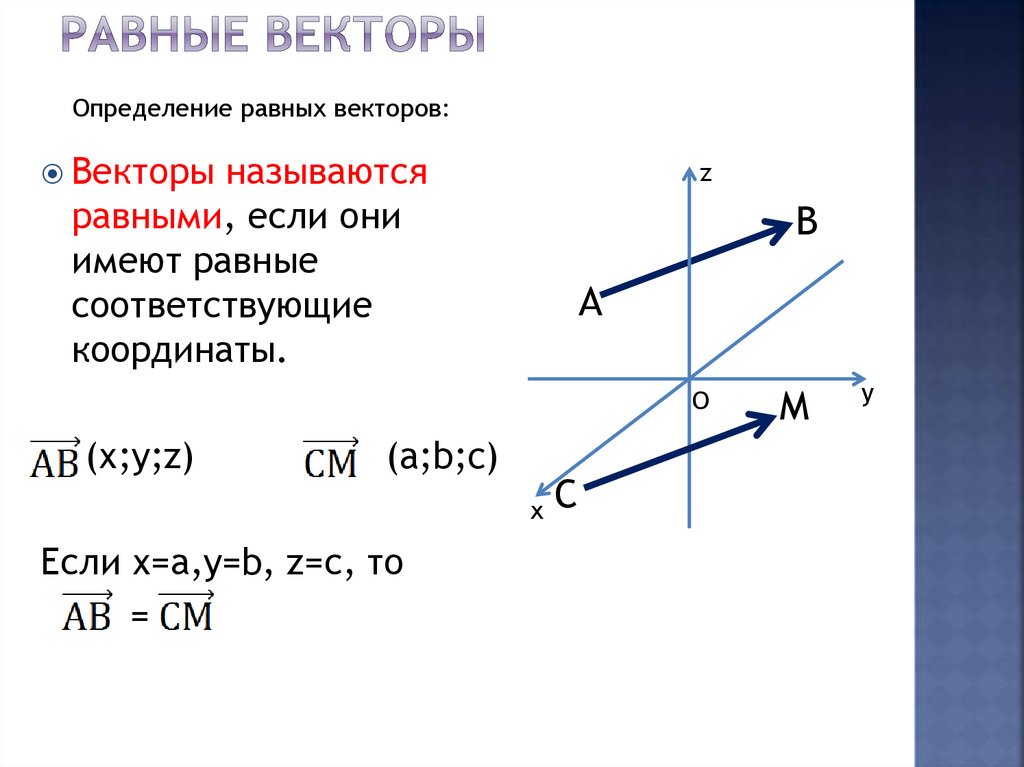
21. Равные векторы

Определение равных векторов:
Векторы называются
z
равными, если они
имеют равные
соответствующие
координаты.
В
А
O
(х;y;z)
(a;b;c)
Если х=а,у=b, z=с, то
=
x С
М
y

22. укажите пары равных векторов

Дано:
А(2;7;-3); В(1;0;3); С(-3;-4;5); М(-2;3;-1)
Определить: пары равных векторов
Решение:
Равны соответствующие координаты у
векторов
,
, значит, они
попарно равны

23. укажите пары равных векторов

Дано:
А(2;7;-3); В(1;0;3); С(-3;-4;5); М(-2;3;-1)
Определить: пары равных векторов
Решение:
Равны соответствующие координаты у
векторов
,
, значит, они
попарно равны

24. Сложение векторов в пространстве

Суммой векторов
вектор
(а;b;с) и (m;n;k) называется
(a+m;b+n;c+k)
Например, найти координаты вектора
если
(-5;3;-9) и
Решение:
(-5+4; 3+(-2); -9+8)
(-1; 1; -1)
(4; -2; 8)
,

25. Сложение векторов в пространстве

Суммой векторов
вектор
(а;b;с) и (m;n;k) называется
(a+m;b+n;c+k)
Например, найти координаты вектора
если
(-5;3;-9) и
Решение:
(-5+4; 3+(-2); -9+8)
(-1; 1; -1)
(4; -2; 8)
,

26. Сложение векторов в пространстве

Суммой векторов
вектор
(а;b;с) и (m;n;k) называется
(a+m;b+n;c+k)
Например, найти координаты вектора
если
(-5;3;-9) и
Решение:
(-5+4; 3+(-2); -9+8)
(-1; 1; -1)
(4; -2; 8)
,

27. Умножение вектора на число

Произведением вектора
(а;в;с) на число
λ называется вектор λ =(λа; λв; λс)
Например, найти координаты вектора
если
Решение:
(5;-1;-2)
,

28. Умножение вектора на число

Произведением вектора
(а;в;с) на число
λ называется вектор λ =(λа; λв; λс)
Например, найти координаты вектора
если
Решение:
(5;-1;-2)
,

29. Умножение вектора на число

Произведением вектора
(а;в;с) на число
λ называется вектор λ =(λа; λв; λс)
Например, найти координаты вектора
если
Решение:
(5;-1;-2)
,

30. Скалярное произведение векторов в пространстве

Скалярным произведением векторов
(х;у;z) называется число
(а;в;с) и
=ax+вy+cz
Например,
найти скалярное произведение векторов
и
Решение:

31. Скалярное произведение векторов в пространстве

Скалярным произведением векторов
(х;у;z) называется число
(а;в;с) и
=ax+вy+cz
Например,
найти скалярное произведение векторов
и
Решение:

32. Скалярное произведение векторов в пространстве

Скалярным произведением векторов
(х;у;z) называется число
(а;в;с) и
=ax+вy+cz
Например,
найти скалярное произведение векторов
и
Решение:

33. Скалярное произведение векторов в пространстве

Скалярным произведением векторов
(х;у;z) называется число
(а;в;с) и
=ax+вy+cz
Например,
найти скалярное произведение векторов
и
Решение: