Введение декартовых координат в пространстве. Формулы середины отрезка и расстояния между двумя точками

1.

Раздел «Координаты и векторы в
пространстве»
Тема: «Введение декартовых координат в
пространстве.
Формулы середины отрезка и расстояния между
двумя точками»

2.

-Вы уже знакомы с прямоугольной
(Декартовой) системой координат на
плоскости, которую
в XIX в. ввёл
французский
математик
Рене Декарт

3.

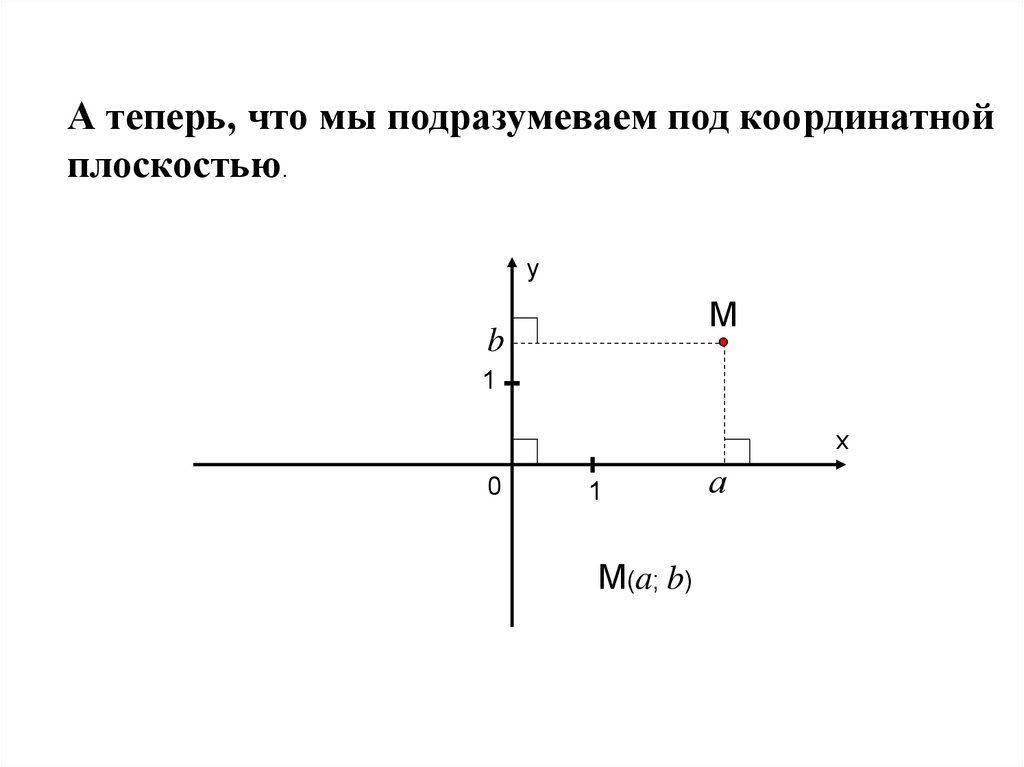
А теперь, что мы подразумеваем под координатной
плоскостью.
у
М
b
1
х
0
1
M(a; b)
а

4.

-А, вот, прямоугольную систему
координат в пространстве ввёл
швейцарский математик
Леонард Эйлер
в XVIIIв.

5.

Выберем в пространстве три
попарно перпендикулярные
координатные прямые x, y, z,
пересекающиеся в одной
точке 0, соответствующей
началу координат каждой оси.
z
Ox Oy Oz
Пунктиром показаны
отрицательные части
осей.
1
1
0
1
y
x
Координатные оси:
Ox – ось абсцисс
Oy – ось ординат
Oz – ось аппликат

6.

В прямоугольной системе координат каждой точке
М пространства сопоставляется тройка чисел –
её координаты: М (х, у, z), где х – абсцисса, у –
ордината, z - аппликата.

7. Построение точек в прямоугольной системе координат

1.
А(3;6;5) На оси Ох- отметить 3
единичных отрезка и провести
прямую через эту точку, причем
параллельную оси Оу
2.
На оси Оу отметить два единичных
отрезка и провести прямую через эту
точку, причем параллельную оси Ох
3.
Через точку пересечения двух прямых
провести прямую параллельную оси
Оz, и отметить на ней 5 единичных
отрезков вверх.
z
А
0
х
3
6
у

8. 1). Если одна из координат точки равна 0, то точка лежит в одной из координатных плоскостей; (например, MOyz, NOxz, KOxy).

Отметим некоторые свойства координат точек:
z
M(0; −2; 3)
3
N(−2; 0; 1)
1
−2
−2
1 S(0; 2; 0)
0
P(2; 0; 0)
1
2
x
−2
3
2
y
K(1; 3; 0)
R(0; 0; −2)
1). Если одна из координат точки равна 0, то точка лежит в одной из координатных
плоскостей; (например, M Oyz, N Oxz, K Oxy).
2). Если две координаты точки равны 0, то точка принадлежит одной из
координатных осей; (например, P Ox, S Oy, R Oz).

9.

Точка лежит
в координатной
на оси
плоскости
Ох
Оу
Оz
Oxy
Oyz
Oхz
(х,0,0)
(0,у,0)
(0,0,z)
(x,y,0)
(0,y,z)
(x,0,z)

10.

z
I
I
I
A(-1; 3;-6)
I
I
I
С
I
I
I
I
В
Найдите координаты
точек А, В, С
I
B(-2;-3; 4)
I
O
I
I
I
I
I
I
x
I
I
I
I
I
I
I
А
I
y
C( 3;-2; 6)

11. Формулы середины отрезка и расстояния между точками на плоскости.

x1 x2 y1 y2
М
;
2
2
АВ
x2 x1 y2 y1
2
2

12. Формулы середины отрезка и расстояния между точками в пространстве.

x1 x2 y1 y2 z1 z 2
М
;
;
2
2
2
АВ
x2 x1 y2 y1 z2 z1
2
2
2

13. Задача № 2.

Дано: А (1;-1;2), В (3;1;-2)
Найдите координаты
середины отрезка АВ и
его длину.

14. Самостоятельная работа №1

1-вариант
2-вариант
№1.
№1.
Отметьте точки в прямоугольной Отметьте точки в прямоугольной
системе координат в
системе координат в
пространстве:
пространстве:
A(2;2;4), В(-3;-4;-5), С(-1;2;-3),
A(3;3;5), В(-4;-3;-5), С(-4;2;3),
О(0;2;3), К(0;0;4).
О(1;-3;0), К(0;5;0).
№2.
№2.
Найдите координаты середины
Найдите координаты середины
отрезка АВ и длину отрезка АВ, отрезка АВ и длину отрезка АВ,
если:
если:
а) А (3;-1), В (-2;4);
а) А (3;4), В (2;-1);
б) А(3;4;-6), В(-5;-3;-8).
б) А(-6;2;-3), В(-4;-6;-9).

15. Тема: «Действия над векторами в пространстве»

16.

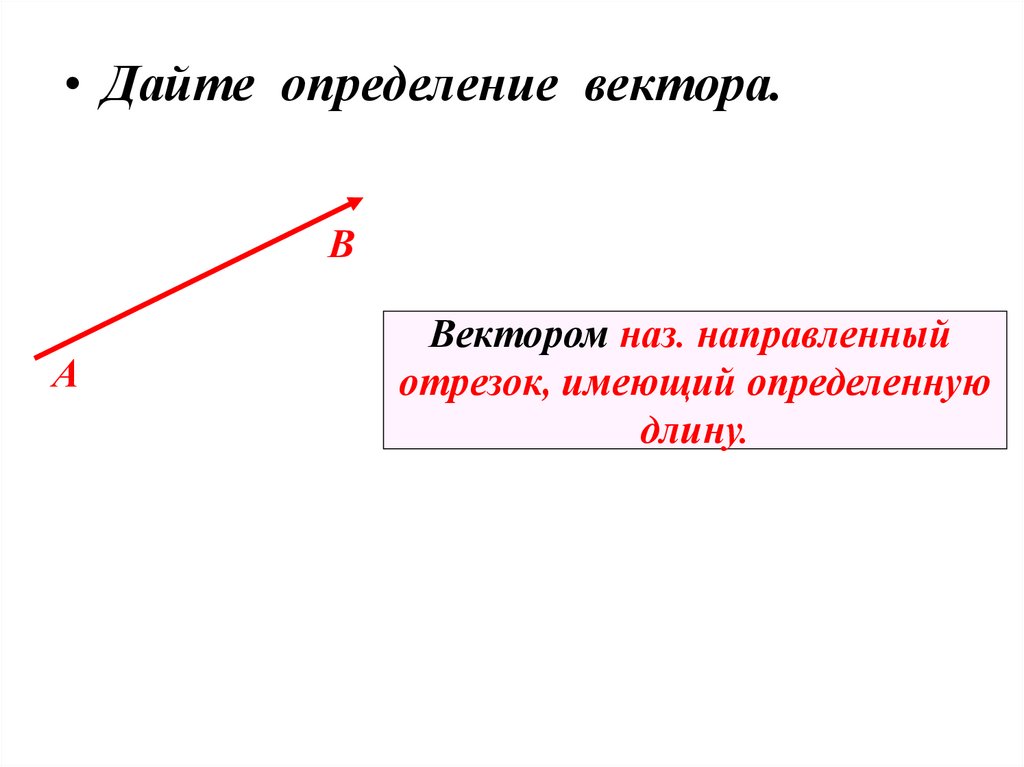
• Дайте определение вектора.
В
А
Вектором наз. направленный
отрезок, имеющий определенную
длину.

17. Координаты вектора в пространстве

Координаты вектора
А(х1;у1;z1) B(x2;y2;z2)
z
В
А
(x2-х1;y2-у1;z2-z1)
Пример:
определить координаты
если М(9;3;-6) и С(-5; 4;-1)
(-5-9; 4-3; -1-(-6))
(-14;1;5)
O
,
x
y

18. Координаты вектора в пространстве

Координаты вектора
А(х1;у1;z1) B(x2;y2;z2)
z
В
А
(x2-х1;y2-у1;z2-z1)
Пример:
определить координаты
если М(9;3;-6) и С(-5; 4;-1)
(-5-9; 4-3; -1-(-6))
(-14;1;5)
O
,
x
y

19. Координаты вектора в пространстве

Координаты вектора
А(х1;у1;z1) B(x2;y2;z2)
z
В
А
(x2-х1;y2-у1;z2-z1)
Пример:
определить координаты
если М(9;3;-6) и С(-5; 4;-1)
(-5-9; 4-3; -1-(-6)) =
O
,
x
(-14;1;5)
y

20.

Два ненулевых вектора называются
коллинеарными, если они лежат на одной прямой
или на параллельных прямых.
Коллинеарные, сонаправленные векторы
c
b
a
a
b
c
b
c
a
Нулевой вектор условились считать
сонаправленным с любым вектором.
o
a
o
c
o
b

21.

Два ненулевых вектора называются
коллинеарными, если они лежат на одной прямой
или на параллельных прямых.
Коллинеарные,
противоположно направленные векторы
b
c
a
a
b
c
b
Если векторы а { x1; y1; z1 } и b { x2; y2; z2 }, то:
х1 у1 z1
k
х2 у 2 z 2

22.

№1.

23.

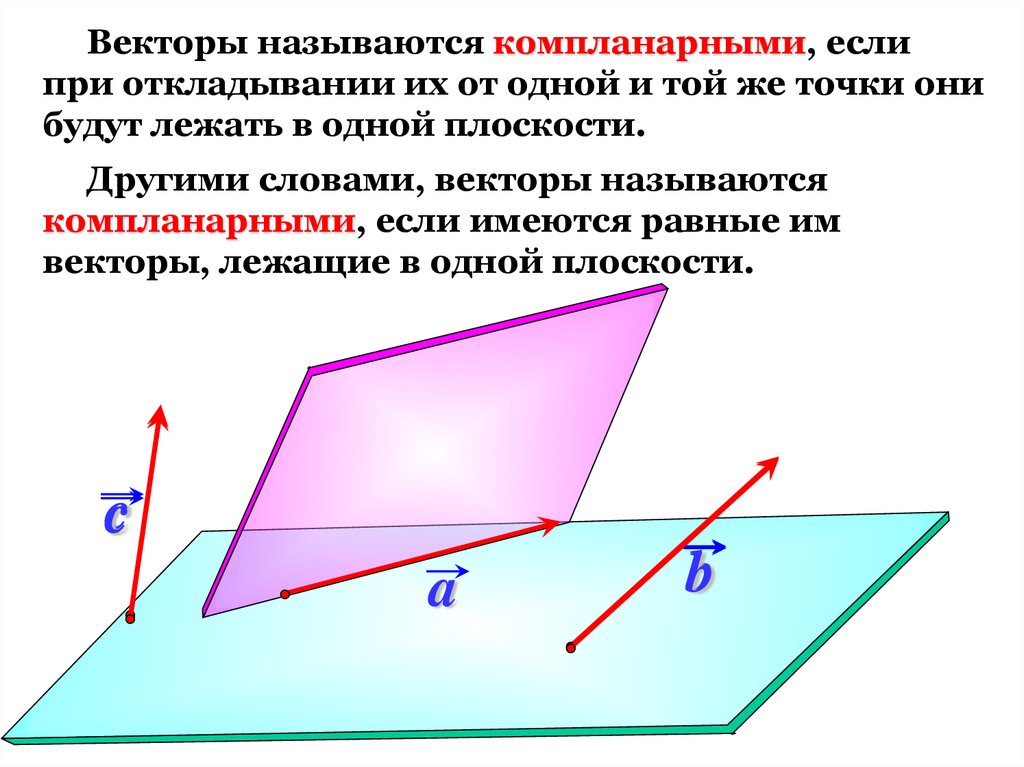
Векторы называются компланарными, если
при откладывании их от одной и той же точки они
будут лежать в одной плоскости.
Другими словами, векторы называются
компланарными, если имеются равные им
векторы, лежащие в одной плоскости.
c
a
b

24.

Любые два вектора компланарны.
Три вектора, среди которых имеются
два коллинеарных, также компланарны.
Признак
компланарности:
c можно разложить по векторам
a и b , т.е. представить в виде c = xa + yb
где x и y – некоторые числа, то векторы a , b и c
Если вектор
компланарны.

25.

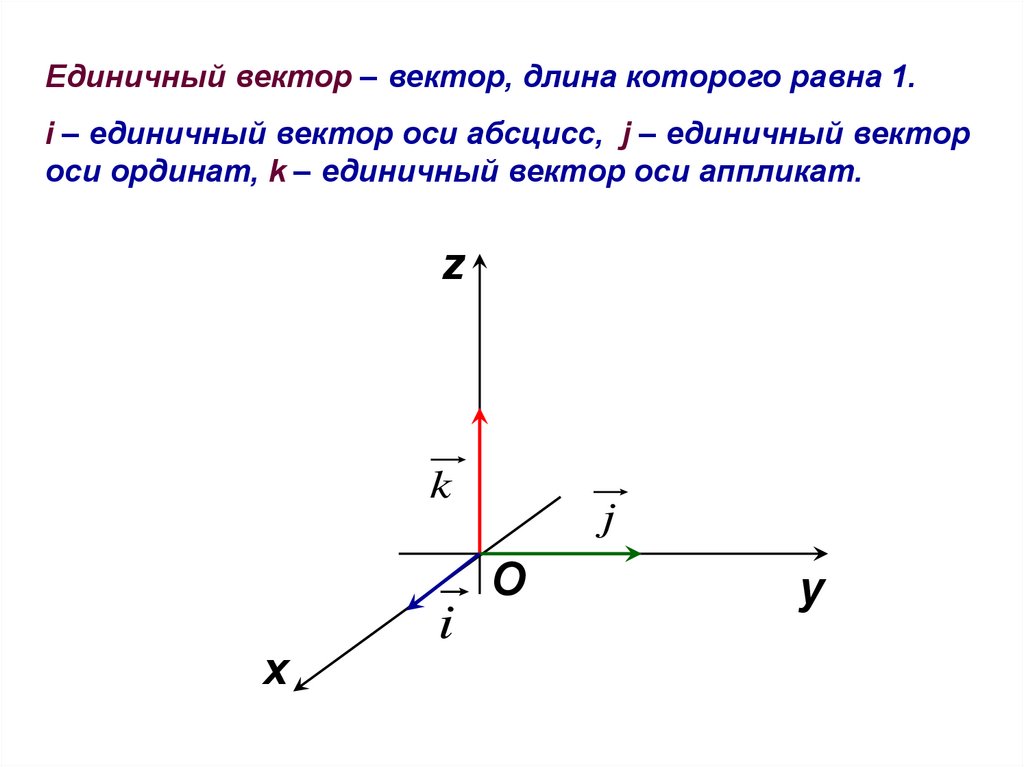
Единичный вектор – вектор, длина которого равна 1.
i – единичный вектор оси абсцисс, j – единичный вектор
оси ординат, k – единичный вектор оси аппликат.
z
k
j
O
i
x
y

26.

Любой вектор ā можно разложить по
координатным векторам, т.е. представить в
виде:
а хi y j z k
где x, y, z –координаты вектора а.
Нулевой вектор можно представить в виде:
0 0i 0 j 0k

27. Решение задач

№2.
№3.

28. Правила действий над векторами с заданными координатами.

1.Равные векторы имеют равные координаты.
а
х
;
у
;
z
1
1
1
Пусть
a
b
,
,
b х2 ; у2 ; z2
тогда
х1 = х2; у1 = у2; z1 = z2

29. Укажите пары равных векторов

№4. Дано: А(2;7;-3); В(1;0;3); С(-3;-4;5); М(-2;3;-1)
Определить: пары равных векторов
Решение:
Равны соответствующие координаты у
Равны соответствующие координаты у
векторов
,
значит, они
векторов
,
, значит, они
попарно равны
попарно равны

30. Правила действий над векторами с заданными координатами.

2. Каждая координата суммы двух (и более)
векторов равна сумме соответствующих
координат этих векторов.
Если
а х1; у1; z1
,
b х2 ; у2 ; z2
то
с х1 х2 ; у1 у2 ; z1 z2
с a b

31. Правила действий над векторами с заданными координатами.

3. Каждая координата произведения вектора на число
равна произведению соответствующей координаты
на это число.
Если
то
а х; у; z , α – произв.число , a с
с х; у; z
4. Каждая координата разности двух векторов равна число
равна разности соответствующих координат на этих
векторов.
Если а х1 ; у1 ; z1 b х ; у ; z
2
2
2
то
с х1 х2 ; у1 у2 ; z1 z2
с a b

32. Выполнить задание устно:

• Даны векторы:
а 3;5; 7
c 0;1;8
b 4; 1;3
d 3;0;0
• Найти вектор равный:
а) 2 а
6;10; 14
б) 3 b
в) a b
7;4; 4
г) b с
4; 2; 5
д) а b d
10;4; 4
12;3; 9
e) 3d 2c
9; 2; 8

33.

№5.
№1.
Д/З.
№6.
№2.
Д/З.

34. Самостоятельная работа №2

1-вариант
2-вариант
№2. Определите коллинеарные ли векторы

35.

Тема: «Скалярное
произведение векторов»

36.

Угол между векторами
Угол между двумя ненулевыми
векторами называется угол между
направлениями этих векторов.
a
)
a
^
b
b
а b

37.

Найдите угол между векторами
a b = 300
a
a c = 1200
d
300
c
b
f
b c = 900
d c = 1800
d f = 00

38. Скалярное произведение векторов

Скалярным
произведением векторов
называется произведение их
длин на косинус угла между
ними.
a
Скалярное произведение векторов –
число (скаляр).
a b a b cos( )

39.

Частные случаи
b
a
a b = 900
=0
a b = a b cos 900 = 0
Скалярное произведение ненулевых векторов
равно нулю тогда и только тогда, когда эти
векторы перпендикулярны.
a b = 0
a b

40.

Скалярное произведение ненулевых векторов
положительно тогда и только тогда, когда угол между
векторами острый.
a b > 0 a b < 900
Скалярное произведение ненулевых векторов
отрицательно тогда и только тогда, когда угол между
векторами тупой.
a b < 0 a b > 900

41.

№7.

42. Формула нахождения скалярного произведения через координаты векторов

a {x1 ; y1 ; z1 }
b {x2 ; y2 ; z2 }
a b = x1x2 + y1y2 + z1z2

43.

Пример
1) Найти скалярное произведение векторов:
a {-6; 9}
b {-1; 0}
a b= x1x2 + y1y2
a b= -6 (-1) + 9 0 = 6

44.

Пример
2)Найти скалярное произведение векторов:
a {0; 0; 4}
b {22; 1; 8}
a b= x1x2 + y1y2 + z1z2
a b= 0 22 + 0 1 + 4 8 = 32

45.

Пример
3)Найти скалярное произведение векторов:
a {1; 7; 9}
b {-2; 4; 0}
a b= x1x2 + y1y2 + z1z2
a b = 1 (-2) + 7 4 + 9 0 = 26

46.

Д/з. Найти скалярное произведение векторов:
1)
a {1; 10; 7} b {0; 7; 0}
2)
a {7; 25; 0} b {11; 0; 54}

47. Формула нахождения угла между векторами через скалярное произведение

cos
x1 x2 y1 y2
x12 y12 x22 y22