Степенева функція

1.

2.

План
1. Означення степеневої функції.
2. Властивості та графік функції y x
p
, де p N
3. Властивості та графік функції y x
p
, де
1
p , к 2;3;4;...
k
4. Властивості та графік функції
y x , де
p
p - ціле від”ємне число.

3.

Як алгебраїсти замість АА, ААА, … пишуть А2, А3, …
1 1 1
так я замість
, 2 , 3 пишу а-1, а-2, а-3, …
а а а
Ньютон І.

4.

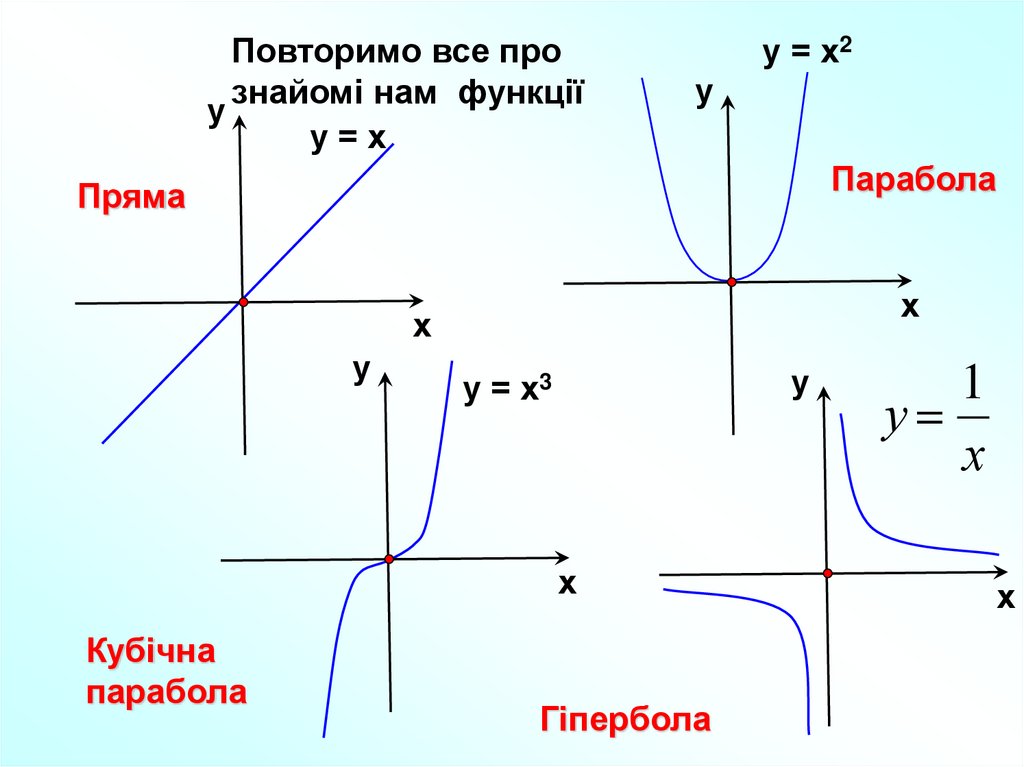
Повторимо все про
знайомі нам функції
у
у=х
у = х2
у
Парабола
Пряма
х
х
у
у
у = х3
х
Кубічна
парабола
Гіпербола
1
у
х
х

5.

у = х,
у = х2,
у = х3,
1
у
х
Всі ці функції є
частковими випадками
степеневої функції
у = хр, де р – задане дійсне число
Властивості і графік степеневої функції
залежать від властивостей степенів з дійсним
показником, а саме від того, при яких значеннях
х і р має зміст степінь хр.

6.

Показник р = 2n – парне натуральне число
у = х2, у = х4 , у = х6, у = х8, …
у
D( y ) : x R
у = х2
Е ( y) : у 0
0
1
х
Графік парної функції
Область определения
значений
симетричний
відноснофункции
осіфункции
Оу. – –
Область
множество
значений,
Графік
непарної
функції
значения,
которые
может
которые может
принимать
симетричний
відносно
початку
принимать
переменная
х
переменная
у О.
координат
– точки
Функція у=х2n парна,
так як (–х)2n = х2n
Функція спадає на
проміжку
( ;0]
Функція зростає
на проміжку
[0; )

7.

y
у = х2
у = х4
у = х6
-1 0 1 2
x

8.

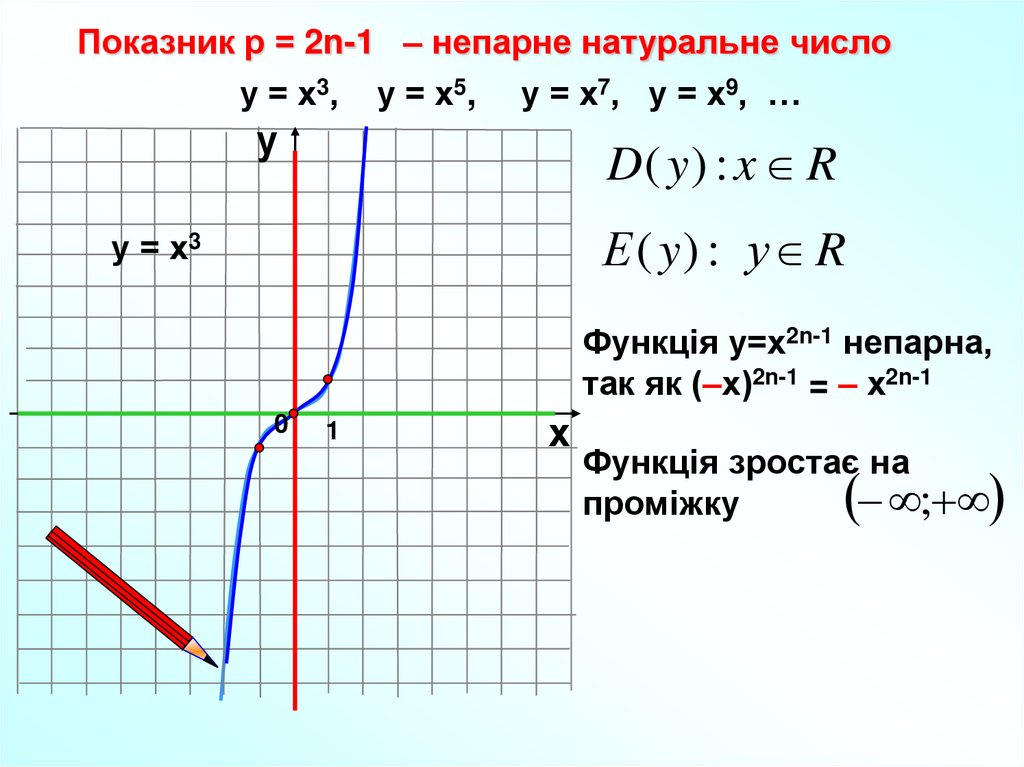
Показник р = 2n-1 – непарне натуральне число
у = х3, у = х5, у = х7, у = х9, …
у
D( y ) : x R
Е ( y) : у R
у = х3
Функція у=х2n-1 непарна,
так як (–х)2n-1 = – х2n-1
0
1
х
Функція зростає на
;
проміжку

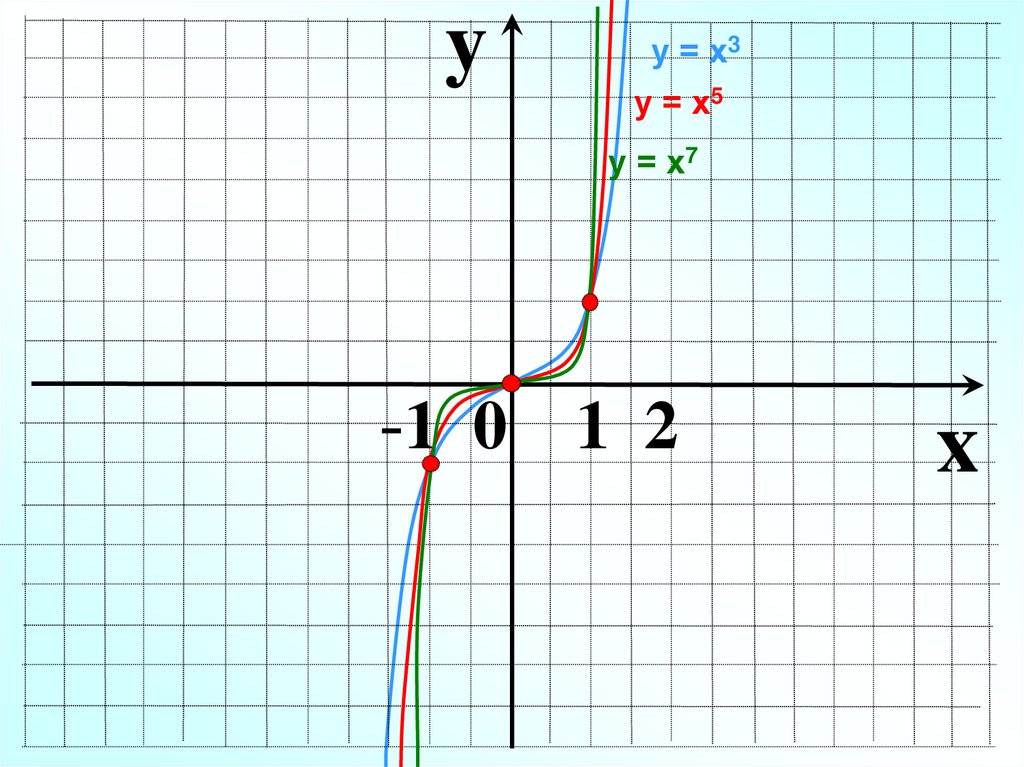
9.

y
у = х3
у = х5
у = х7
-1 0 1 2
x

10.

Показник р = – 2n, де n – натуральне число
у = х-2, у = х-4 , у = х-6, у = х-8, …
у
D( y ) : x 0
Е ( y) : у 0
0
y х
2
1
1
y 2
х
х
Функція у=х2n парна,
так як (–х)-2n = х-2n
Функція зростає на
проміжку
( ;0)
Функція спадає
на проміжку
(0; )

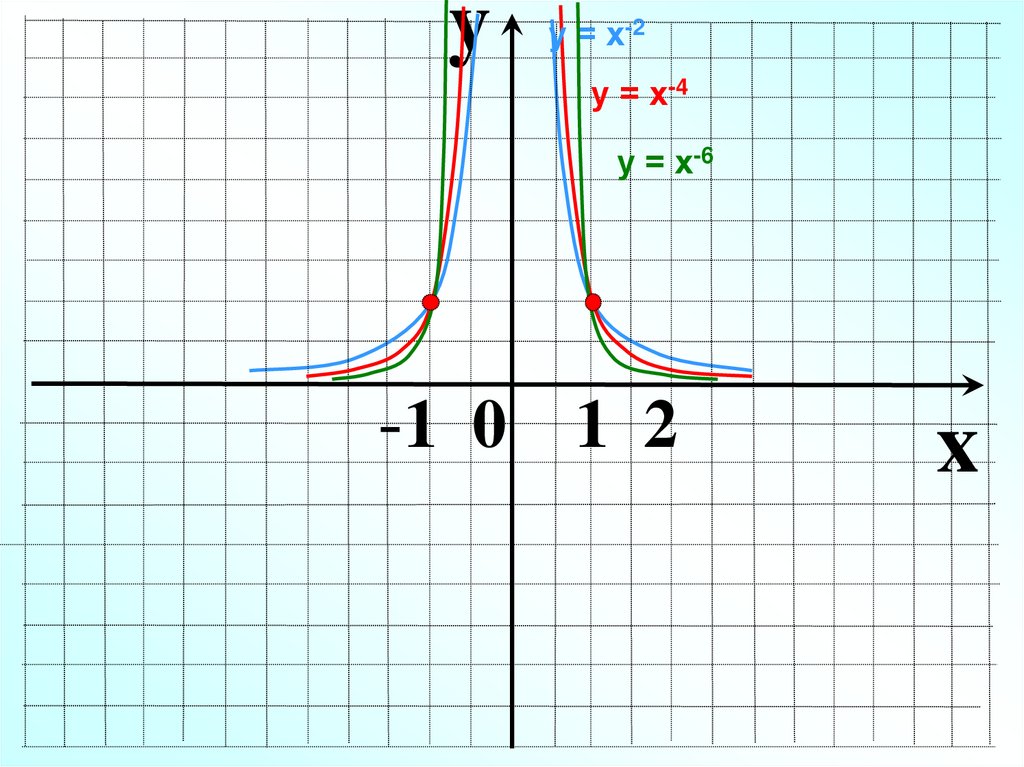
11.

y у=х
-2
у = х-4
у = х-6
-1 0 1 2
x

12.

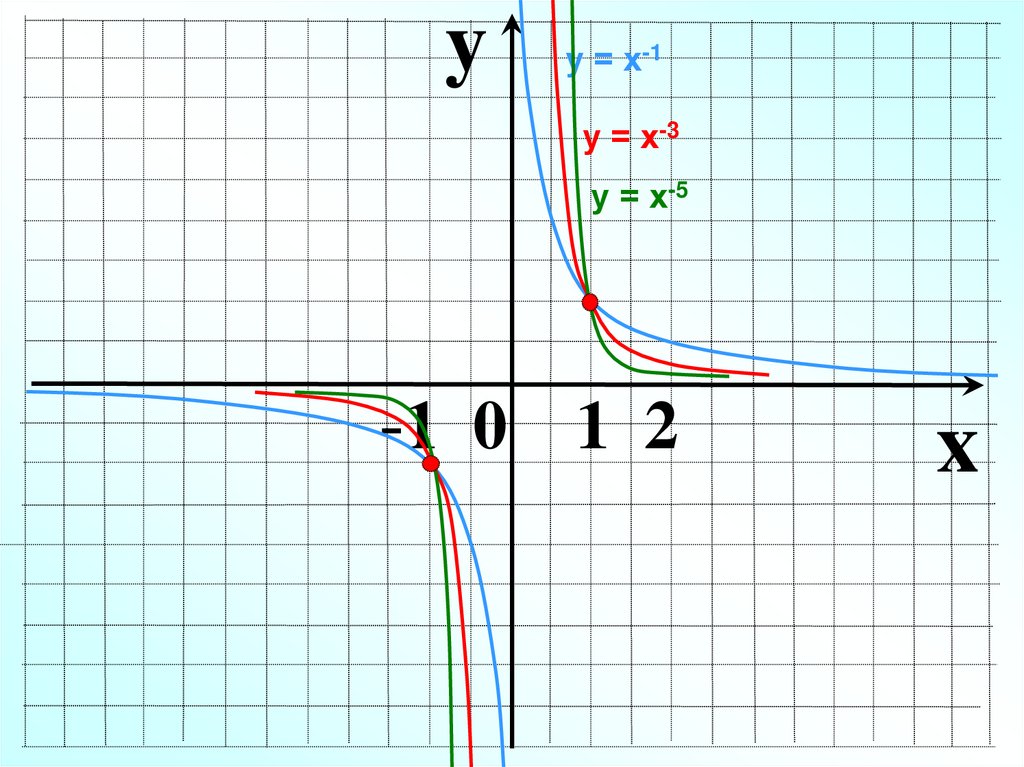
Показник р = – (2n-1), де n – натуральне число
у = х-3, у = х-5 , у = х-7, у = х-9, …
у
D( y ) : x 0
Е ( y) : у 0
0
х
1
Функція у=х-(2n-1)
непарна, так як
(–х)–(2n-1) = –х–(2n-1)
Функція спадає на
y х
1
1
y
х
проміжку
( ;0)
Функція спадає
на проміжку
(0; )

13.

y
у = х-1
у = х-3
у = х-5
-1 0 1 2
x

14.

Показник р – додатне дійсне неціле число
у
у = х1,3,
у х
у = х0,7, у = х2,12,
0
1
у х …
D( y ) : x 0
4
3
у х
1
3
1
3
Е ( y) : у 0
Функція зростає на
х проміжку
[0; )

15.

y
у = х0,84
у = х0,7
у = х0,5
-1 0 1 2
x

16.

y
у = х3,1
у = х2,5
-1 0 1 2
у = х1,5
x

17.

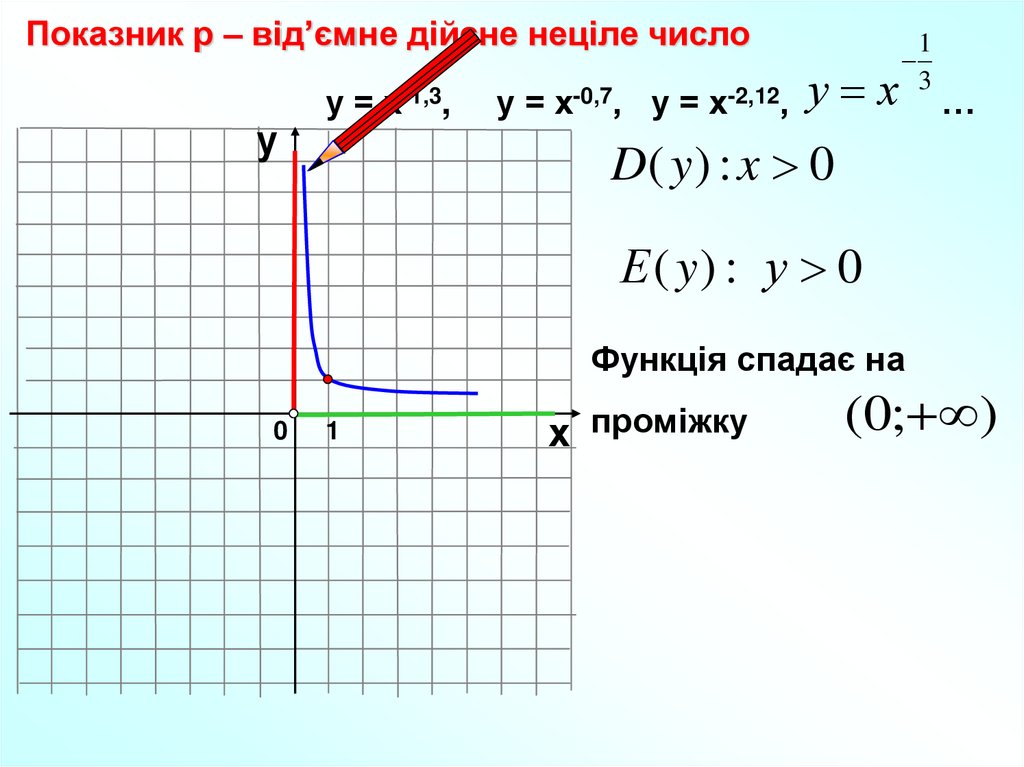
Показник р – від’ємне дійсне неціле число
у
у = х-1,3,
у = х-0,7, у = х-2,12, у х
1
3
…
D( y ) : x 0
Е ( y) : у 0
Функція спадає на
0
1
х проміжку
(0; )

18.

y
у = х-2,3
у = х-1,3
у = х-3,8
у = х-0,3
-1 0 1 2
x

19.

у
у
у х
0
у х
1
4
3
1
3
х
0
1
х
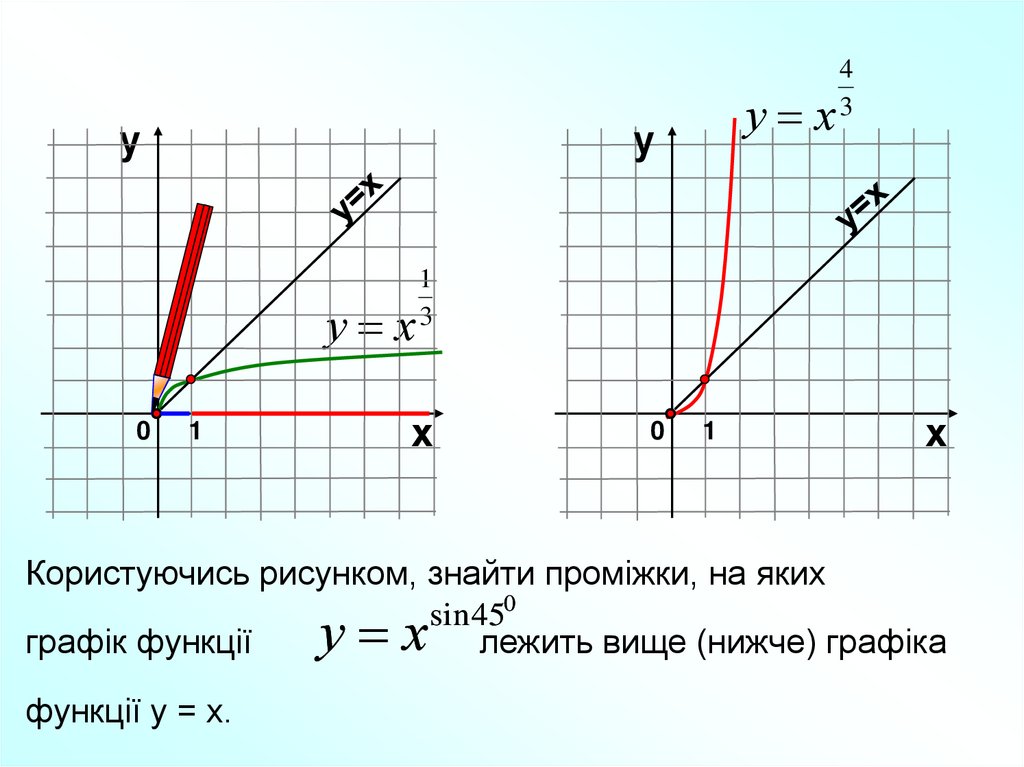
Користуючись рисунком, знайти проміжки, на яких
графік функції
у х лежить вище (нижче) графіка
функції у = х.

20.

у
у
у х
0
у х
1
4
3
1
3
х
0
1
х
Користуючись рисунком, знайти проміжки, на яких
графік функції
функції у = х.
у х
sin 450
лежить вище (нижче) графіка

21.

Користуючись рисунком, знайти проміжки, на яких
1
графік функції
лежить вище (ничже) графіка
у х
функції у = х.
у
у
у
у х0
0
у х
1
1
3
х
1
4
3
х
0
1
х

22.

y
у = х-4
-1 0 1 2
у = (х – 2)-4
x

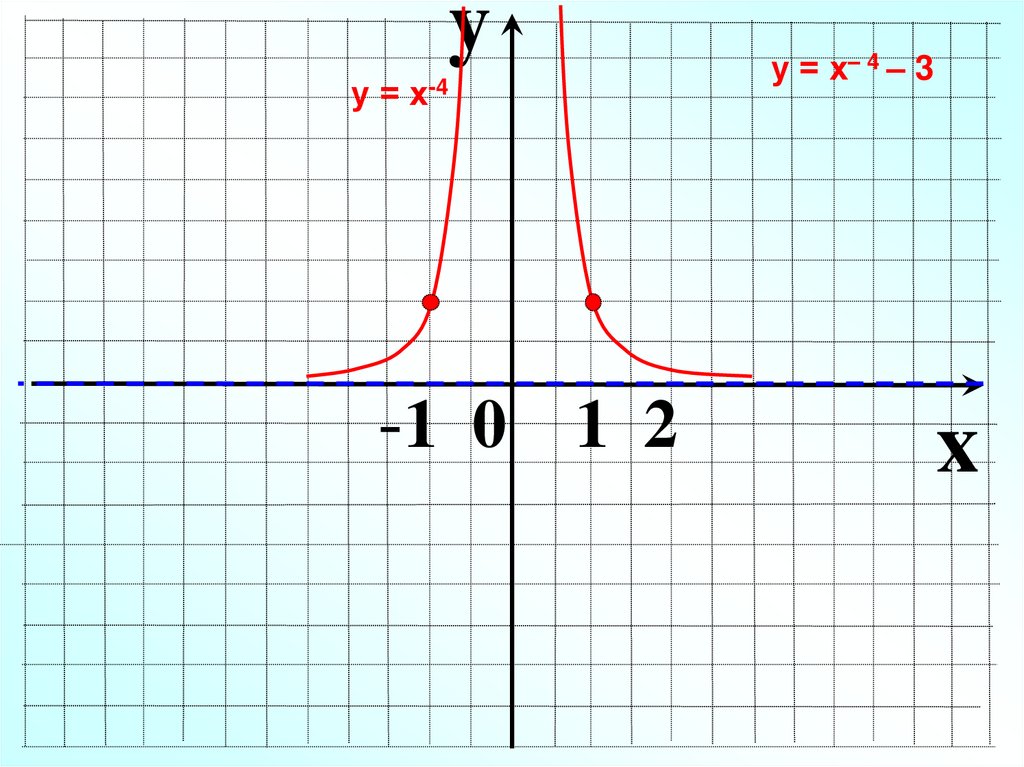
23.

y
у = х-4
-1 0 1 2
у = х– 4 – 3
x

24.

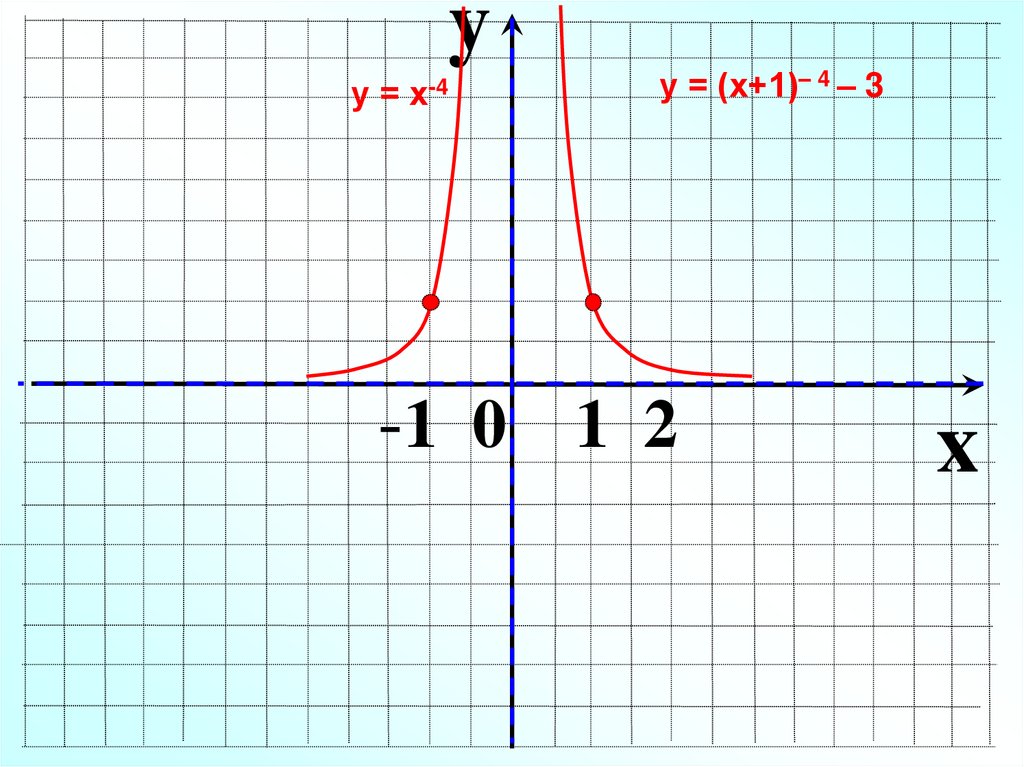
y
у = х-4
у = (х+1)– 4 – 3
-1 0 1 2
x

25.

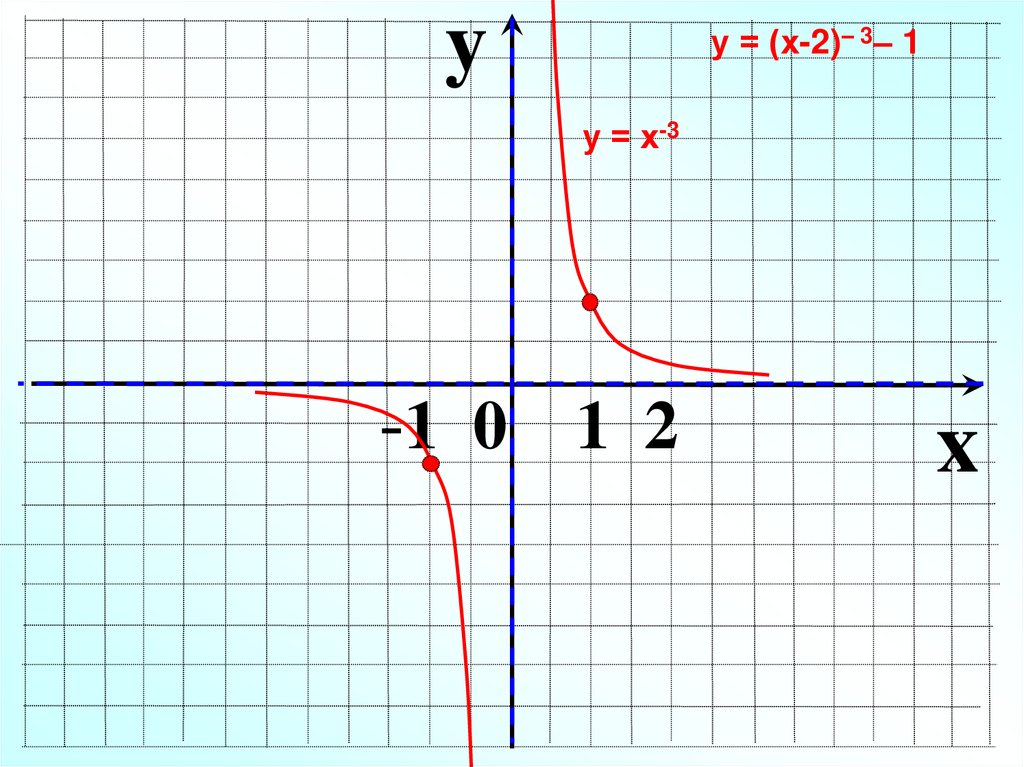
y
у = (х-2)– 3– 1
у = х-3
-1 0 1 2
x

26.

y
у = (х+2)–1,3 +1
у = х-1,3
-1 0 1 2
x