Степенева функція (урок, 10 клас)

1. Степенева функція 10 клас Академічний рівень

Підготувала:
Холоменюк Олена Олексіївна,
вчитель математики
Неморозької ЗОШ І-ІІ ступенів
Звенигородської районної ради

2. Сьогодні на уроці ми:

Повторимо поняття степеня
Повторимо властивості степенів
Ознайомимось з означенням степеневої
функції
Ознайомимось з поняттям властивостей
степеневої функції
Навчимося будувати графіки степеневих
функцій
Навчимося використовувати властивості
функцій для розв'язування задач.

3. Завдання математичного диктанту

1.
2.
3.
4.
Радикали: з ; 3 3 ; 4 3 можна звести до
радикалів 12-го степеня так…
Знизити степінь радикалів 18 362 ; 9 56
можна так: …
Вираз ( 10 а3) 3 можна спростити так: …
Вираз 5 а можна подати так: … при а 0

4. Відповіді до математичного диктанта

1.
2.
3.
4.
12
9
6
3
36
10
a9
10
a
12
3
37
52
12
37

5. Сучасні позначення (типу а , а ) введено в XVII ст. Р. Декартом (1596–1650)

Сучасні
позначення
5
3
(типу а , а )
введено в
XVII ст. Р.
Декартом
(1596–1650)

6. С. Стевін запропонував розуміти під корінь .

С. Стевін
запропонував
розуміти під
п
а корінь а.
1
п

7. Дробові та від’ємні показники степеня першим став застосовувати І. Ньютон (1643—1727).

8. Означення степеневої функції

Функція виду у = х,a де α — будь-яке
дійсне число, називається
степеневою функцією
Розрізняють види, в залежності від n є N:
n=2к n=2к+1
y x
2ê
y x
2 к 1

9. Графіки функцій

y x 2 к 1
y x 2к
у
у
y x 2 к 1
y x 2к
1
0
1
0
y x 2к
1
1
Х
Х
Проходить через початок відліку O(0;0)
Симетричний відносно ОУ
Симетричний відносно (0;0)

10.

Властивості функції
y x
2к
y x
2 к 1
1.Область визначення: R
2. Область значень: y ≥ 0
2. Область значень: R
2. Нулі функції :(0;0)
3.Інтервали знакосталості
Функція додатна, при х ≠ 0
3.Інтервали знакосталості
Функція додатна, при х > 0
Функція від'ємна, при х < 0
5. Парність: парна
5. Парність: непарна

11.

Властивості функції
y x
2к
y x
2 к 1
5.Інтервали зростання
(спадання):
Зростає при х 0
Спадає при х
0
5.Інтервали зростання
(спадання):
Зростає при хєR
6.Найбільше і найменше
значення функції:
Найменше у=0, при х=0
Найбільшого не має
6.Найбільше і найменше
значення функції:
Найменшого не має
Найбільшого не має

12. Перетворення графіків функцій

y x
2 к 1
y x
у
0
2 к 1
у
Х
0
Х

13. Перетворення графіків функцій

y x
2к
y x
у
0
2к
у
Х
0
Х

14. Приклад розв'язування

Побудуйте графік функції:
у = х 5 + 1;
1)Будуємо графік у = х
5
2)Потім паралельно переносимо
його вздовж осі Оy на +1 .

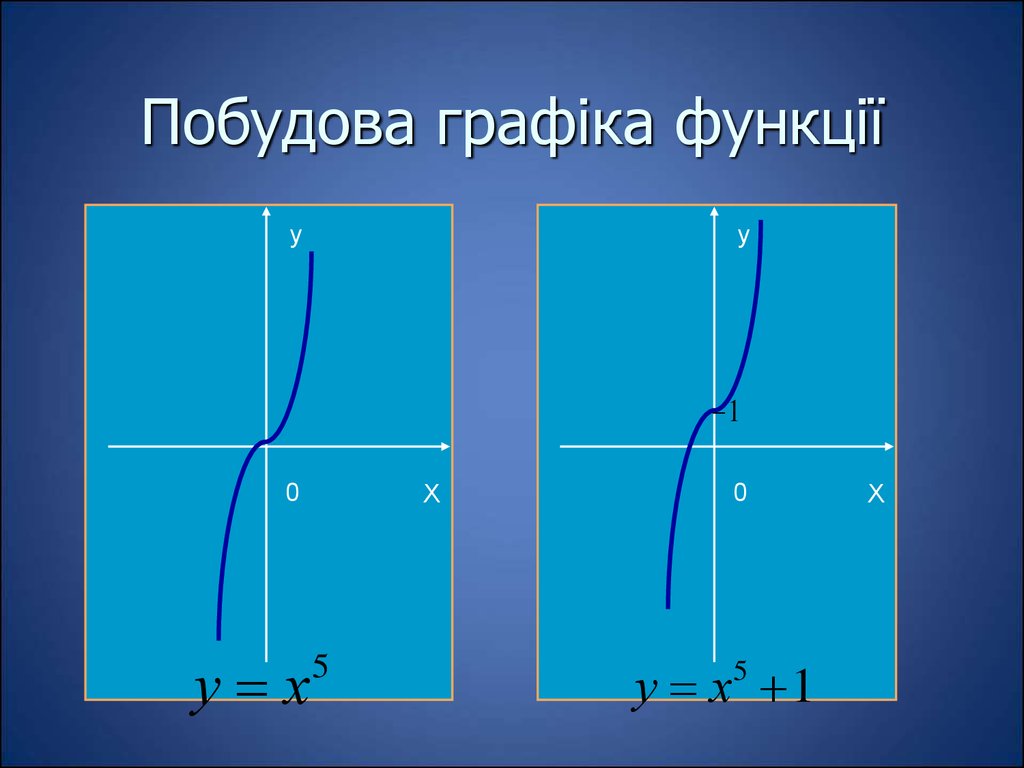
15. Побудова графіка функції

у
у
1
Х
0
у х
5
0
у х 1
5
Х

16. Знайдіть область визначення функції

1
3
1.
y ( x 3)
2.
1
y ( x 2)
3

17. Приклад розв'язування

1) х – 3 0, тобто х 3, отже,
D (y) = [3; +∞).
2) x + 1 > 0, тобто x > –1, отже,
D (y) = (–1; +∞).

18. Домашнє завдання

1. Наведіть приклади реальних
процесів, які описуються за
допомогою степеневих функцій.
2. Параграф 12; Нєлін Є.П. Алгебра
10 кл. (академічний рівень) Харків:Гімназія 2010р.
3. №2 а), в); №5* ст.204.

19. Урок завершено! Бажаю всім успіхів!

20. Використана література

1.Мерзляк А.Г., Номіровський Д.А., Полонський
В.Б., Якір М.С. Алгебра і початки аналізу. 10
кл.(академічний рівень) - Харків: Гімназія
2010р.
2.Бевз Г.П. Алгебра 10 кл. (академічний рівень)
- Харків:Гімназія 2010р.
3.Нєлін Є.П. Алгебра
10 кл. (академічний
рівень) - Харків:Гімназія 2010р.