Похожие презентации:
Механика, кинематика и динамика. Вращение, колебания и волны. Молекулярная физика. Термодинамика
1.
asadullin.fanur@yandex.ruАсадуллин Фанур Фаритович
2.
• МЕХАНИКА.КИНЕМАТИКА и ДИНАМИКА.ВРАЩЕНИЕ. КОЛЕБАНИЯ и ВОЛНЫ.
МОЛЕКУЛЯРНАЯ ФИЗИКА.
ТЕРМОДИНАМИКА.
ЭЛЕКТРИЧЕСТВО.ПОСТОЯННЫЙ ТОК.
Литература:
1.Трофимова Т.И.Курс физики.
2.Трофимова Т.И.Сборник задач по физике с
решениями.
3.Калашников Н.П.и Кожевников
Н.М.Физика. Интернет тестирование.
3.
4.
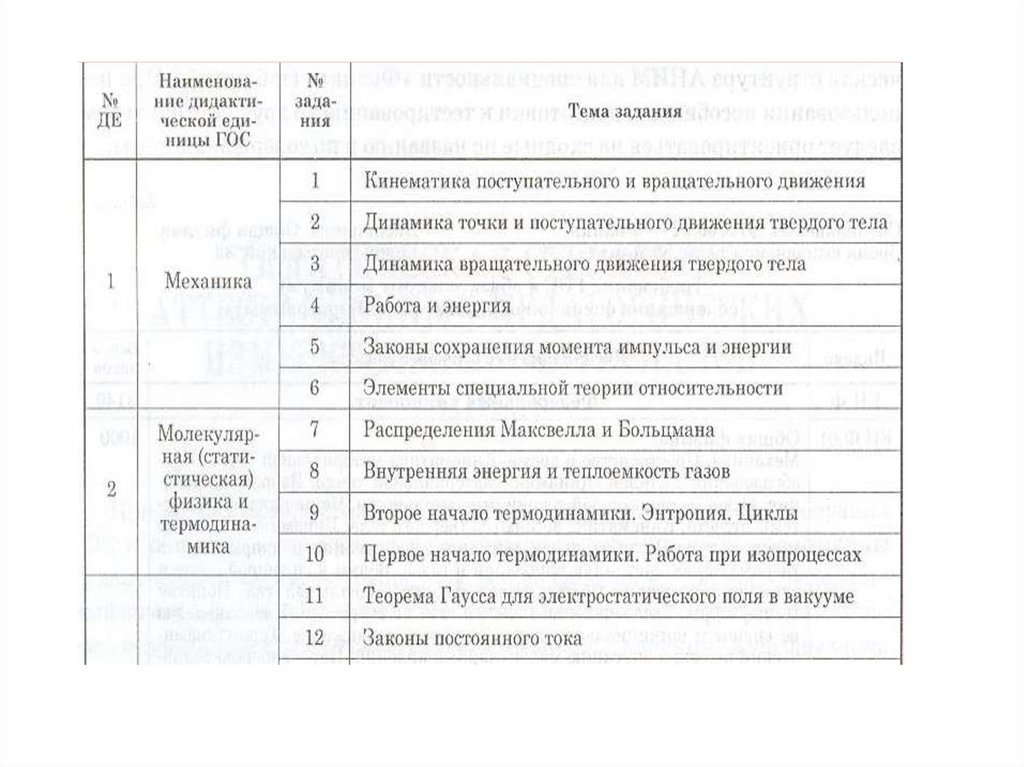
• Понятия кинематики: материальная точка,траектория, путь, перемещение, уравнение
движения. Способы задания уравнений
движения. Скорость. Ускорение.
Z
Координатный способ
x x(t )
y y (t )
z z (t )
y
X
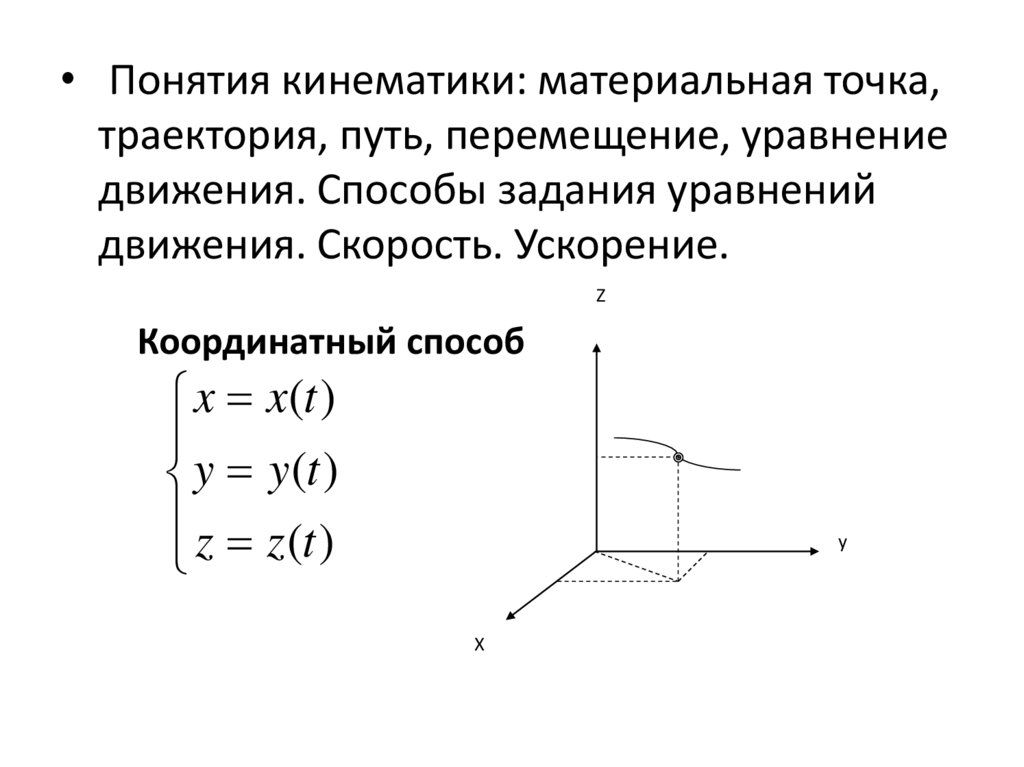
5.
x a cos( t )y b sin( t )
z
c
t
6.
• 2) Естественный- задаётся кривая сострелками по которым движется точка,
стрелка показывает направление обхода
кривой.
S=f(t)
2
at
S V0t
2
S<0
0
S>O
0
7.
• 3)Векторный (главный) способZ
r r (t )
i
k
O
r
r dr
j
X
r i x j y k z
Y
8.
r i a cos( t ) j b sin( t ) k ctZ
O
Y
X
9.
• Скорость и ускорениеdr
V
dt
dV
a
dt
dr
r
i x j y k z
dt
a r i x j y k z
10.
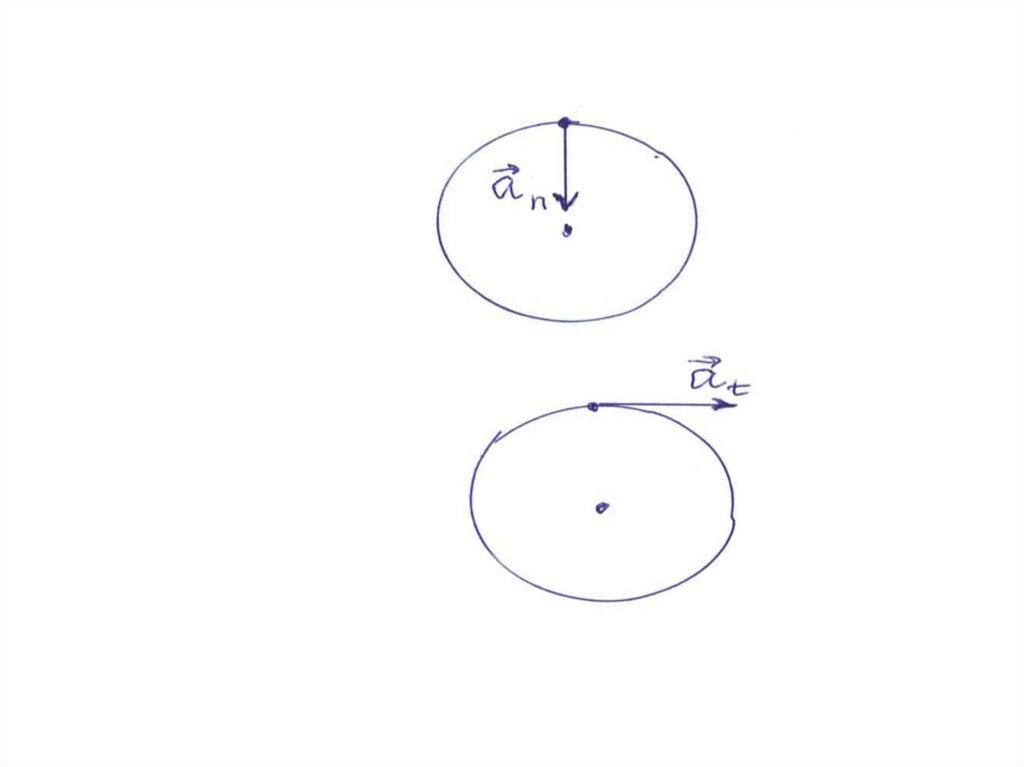
Движение по кривой.Тангенциальное и нормальное ускорения.
a r at an
11.
12.
13.
В векторной форме
an
2
V
an n
r
at r
dV
at
dt
14.
В скалярной форме (без вектора)
an r
2
2
V
an
r
dV
at
dt
at r
15.
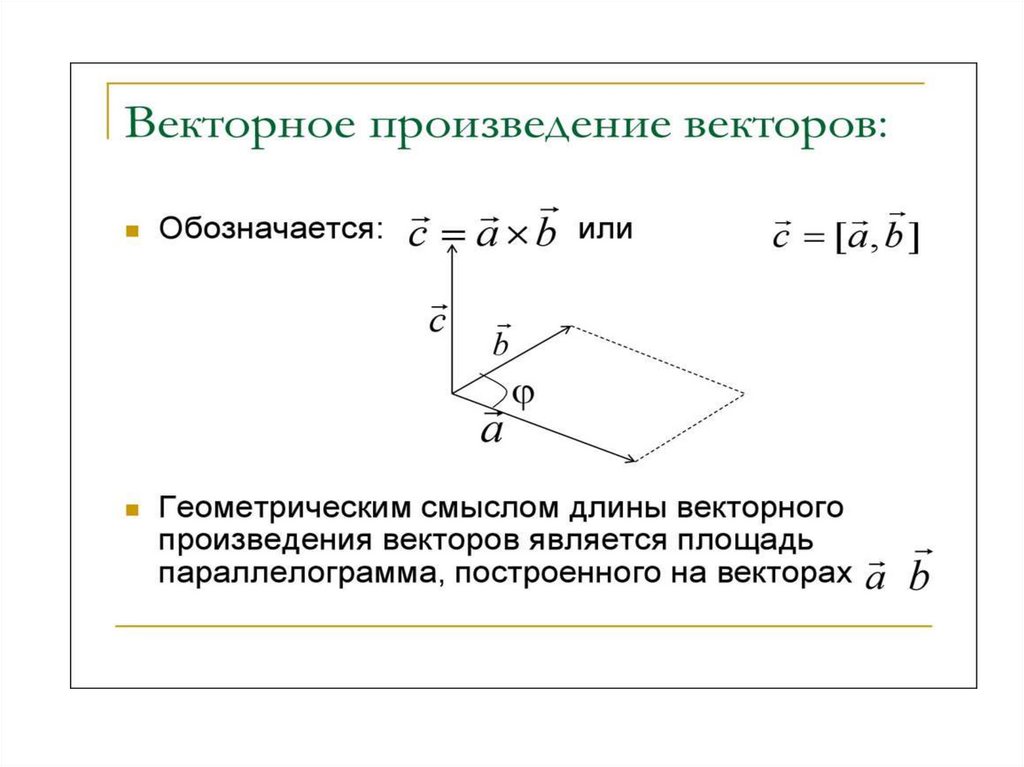
Направления векторов в векторном
произведении определяется правилом
правого буравчика.
Модуль векторного произведения
r
определяется по формуле
r sin( ,̂ r )
16.
17.
18.
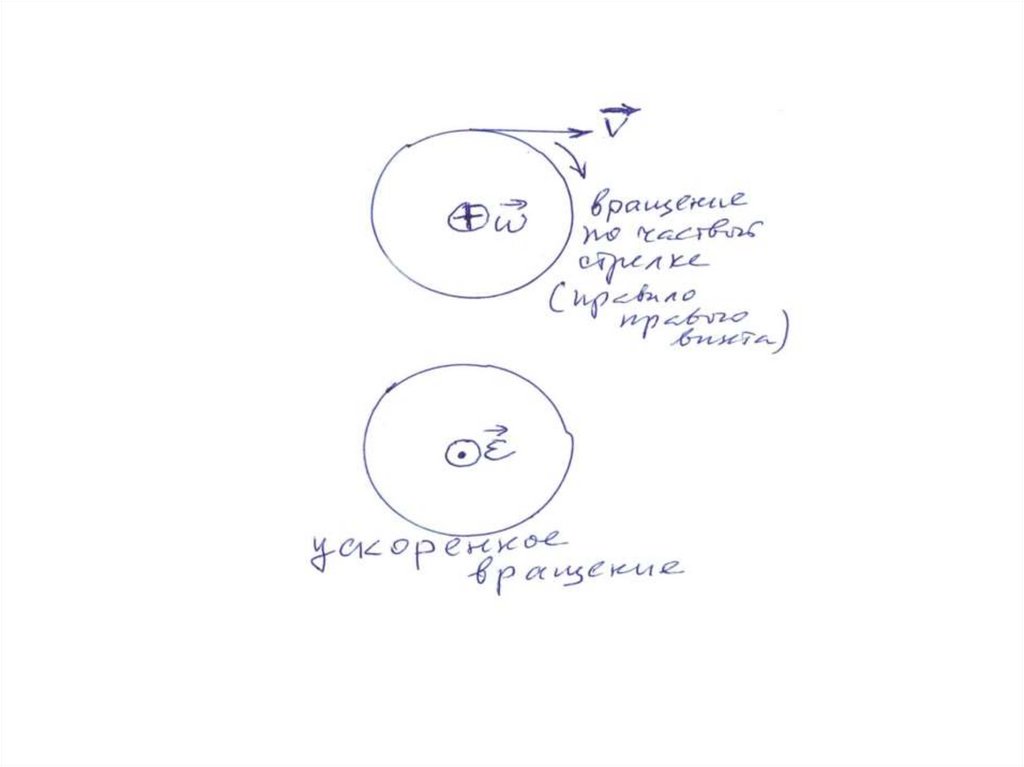
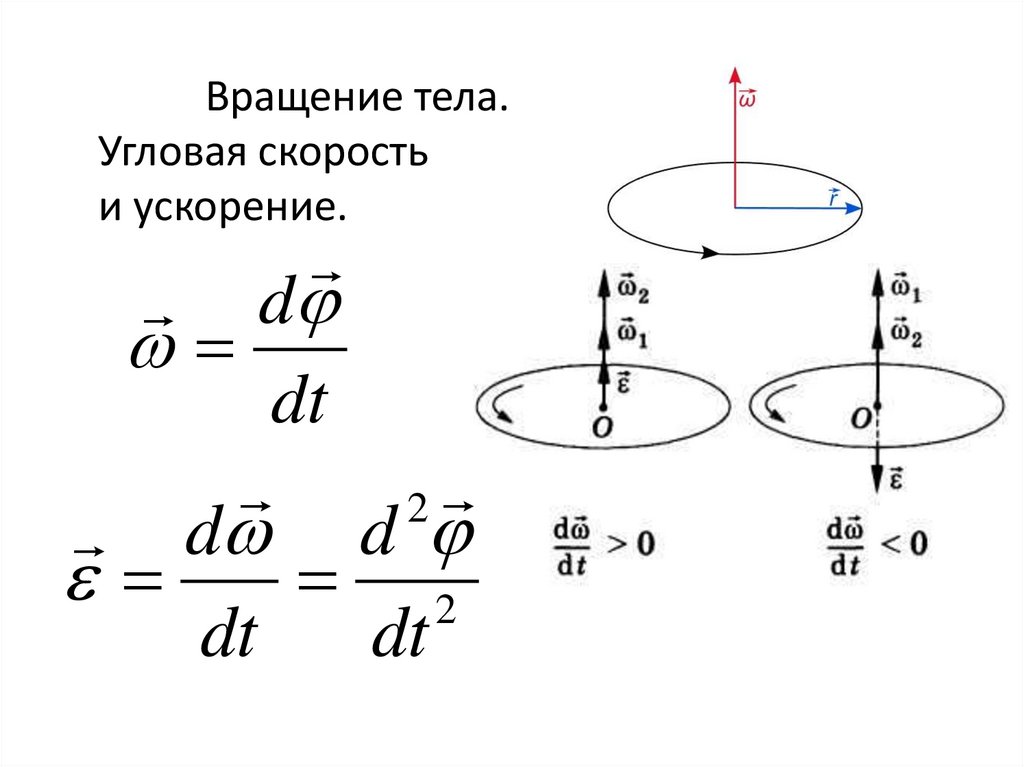
Вращение тела.Угловая скорость
и ускорение.
d
dt
2
d d
2
dt
dt
19.
Момент силы и момент импульса.Момент инерции.
M [r F ]
M J
L [r p]
L J
J mr
2
20.
• Вектор момента силы и угловое ускорение.M [r F ]
M J
M
21.
• Вектор момента импульса и угловаяскорость
L [r p]
L J
L
22.
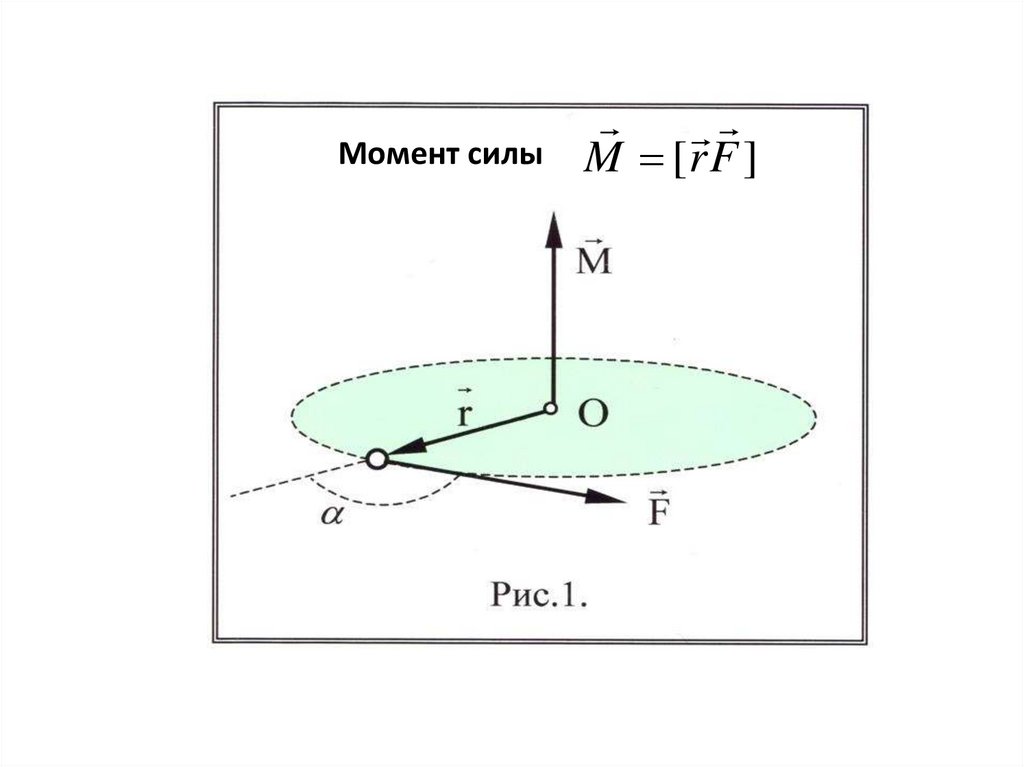
Момент силыM [r F ]
23.
M r FM 0
M r F sin
180градусов
dL
M
dt
L const
24.
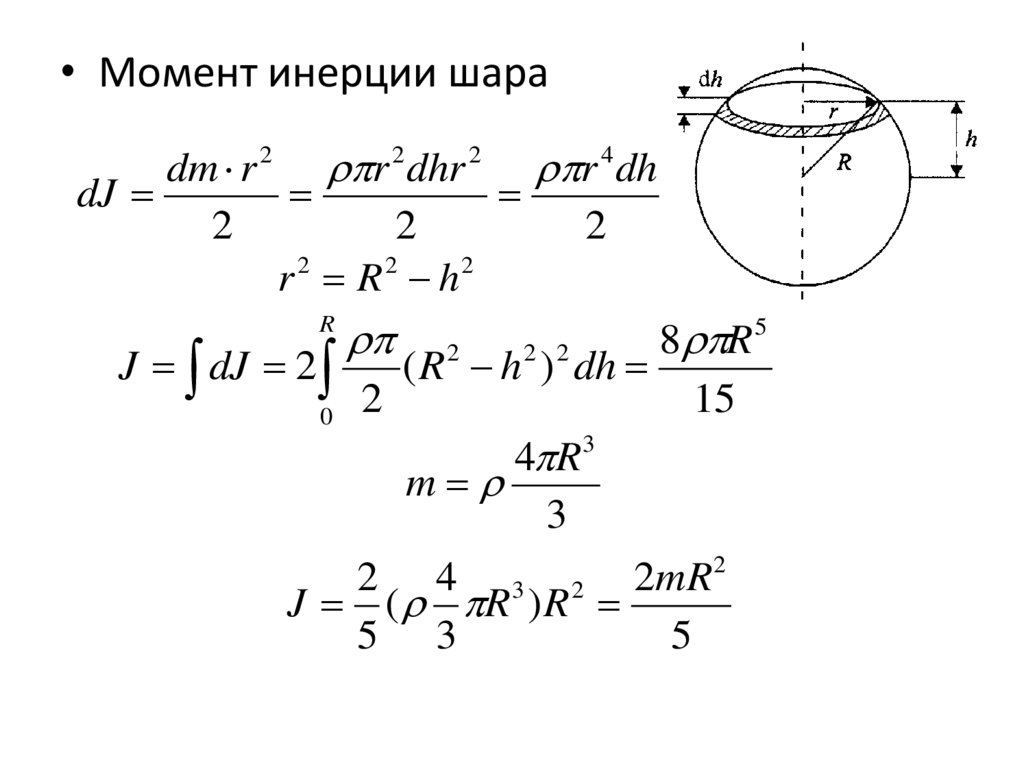
• Момент инерции шараdm r
r dhr
r dh
dJ
2
2
2
r 2 R 2 h2
2
2
4
8 R
J dJ 2
( R h ) dh
2
15
0
4 R 3
m
3
2 4 3 2 2mR2
J ( R ) R
5 3
5
R
2
2
2 2
5
25.
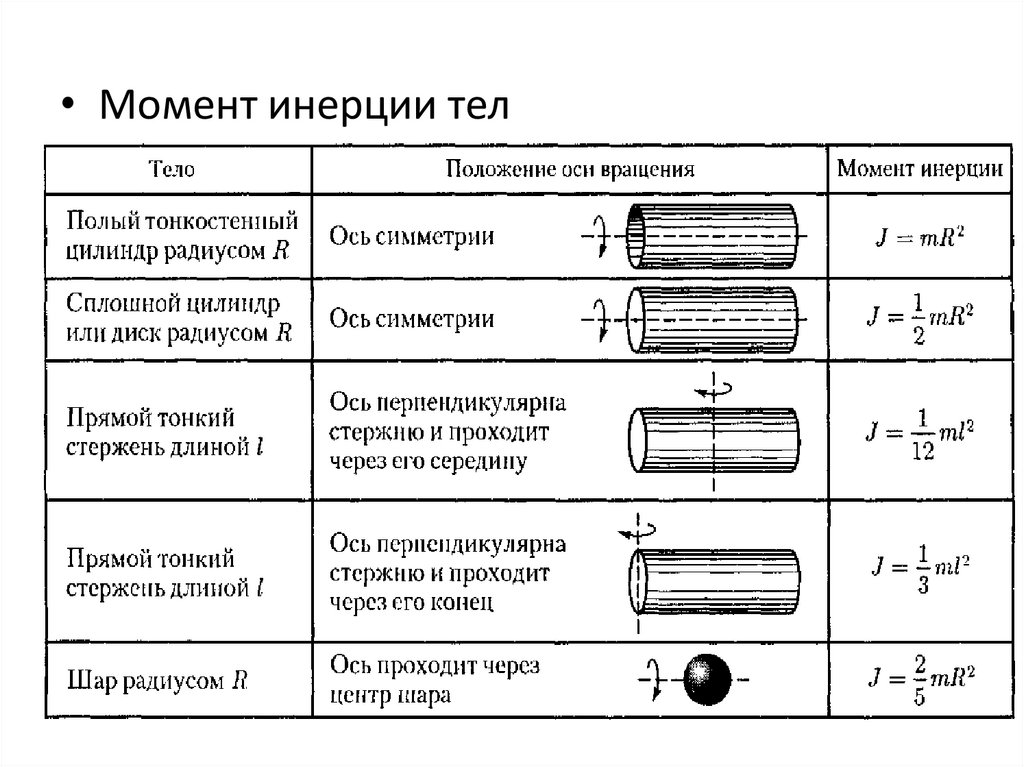
• Момент инерции тел26.
ДИНАМИКА
Законы Ньютона. Механическая система.
Центр масс системы материальных точек и
закон его движения.
Центром масс (или центром инерции)
системы материальных точек называется
воображаемая точка С, положение которой
характеризует распределение массы этой
системы.
n
n
n
m
r
m
V
i i
mi ai
i
i
1
• rC 1
1
VC
a
C
m
m
m
27.
dA ( Fdr ) Fdr cosРабота и Энергия
dA dT
dA dП
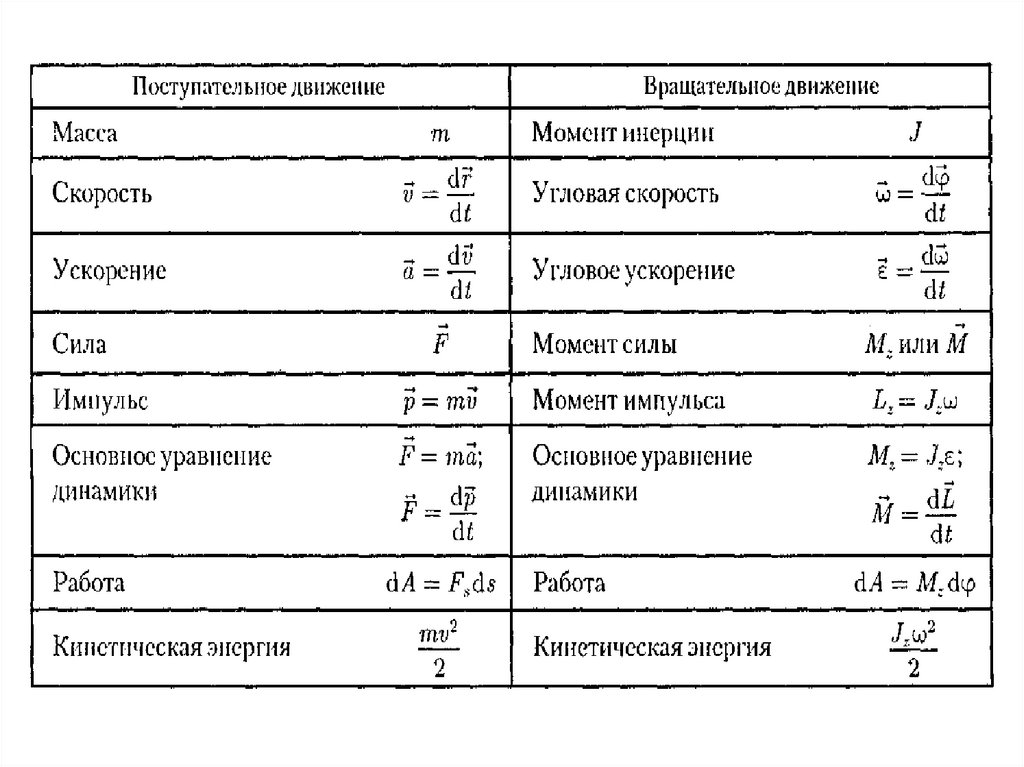
Кинетическая энергия поступательного
и вращательного движения
mV
T
2
2
J
T
2
2
28.
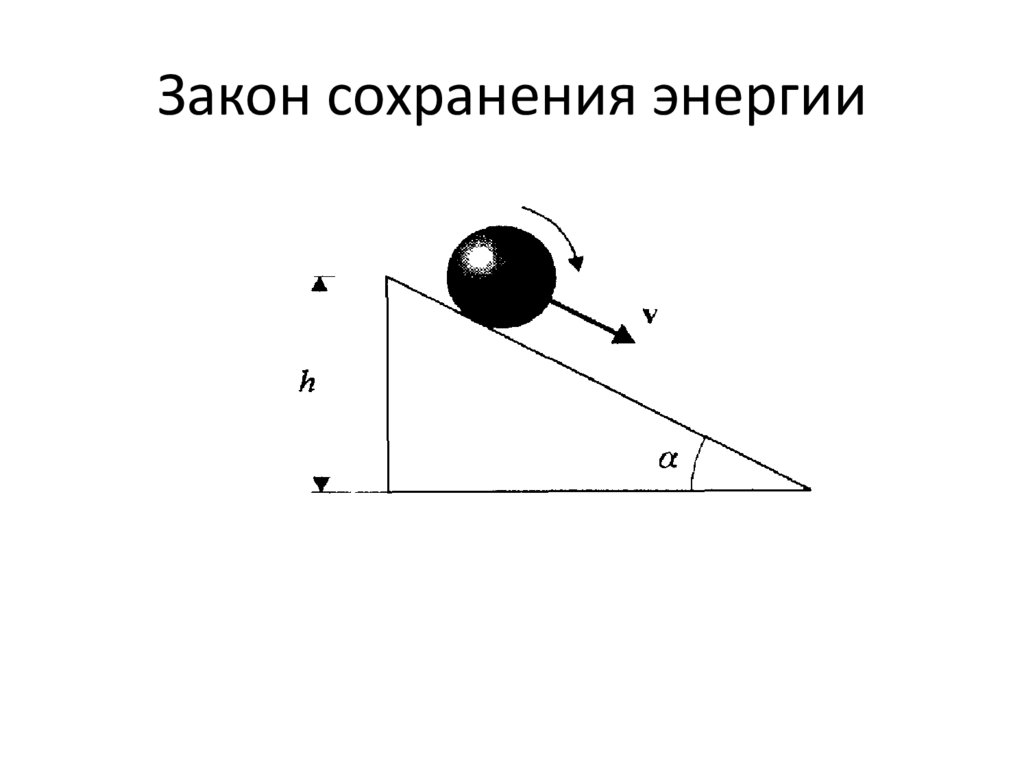
Закон сохранения энергии29.
mV 2 J 2mgh
2
2
2mr 2
J
5
V
r
10gh
V
7
at 2 Vt
h
l
2
2 sin
2h
2
7h
t
V sin sin 10 g
30.
Абсолютно упругий удар шаров31.
Абсолютно неупругий удар32.
33.
Свободные колебания.m x Fx
Fx kx
m x kx
m x kx 0
x 0 x 0
x A sin( 0t )
2
k
2
0
m
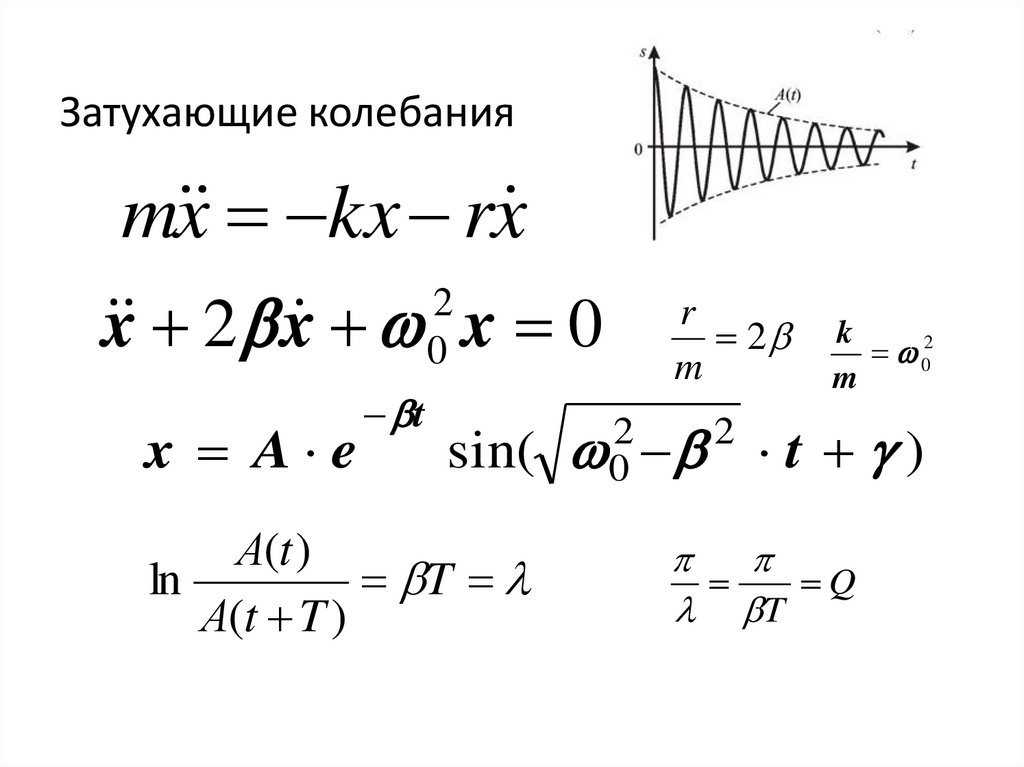
34.
Затухающие колебанияm x kx rx
2
x 2 x 0 x 0
x A e
t
sin(
А(t )
ln
T
А(t T )
r
2
m
k
02
m
2
2
0 t )
Q
T
35.
• Вынужденные колебания.i t
m x kx rx F0 e
2
i t
x 2 x 0 x f 0e
x x1 x2
x1 A e
t
x2 a e
e
i t
sin(
i 1
2
2
0 t )
i t
cos( t ) i sin( t )
36.
̂x ia ei t2
xˆ a 2 2 ei t
2
i t
i t
aˆ e 2 iaˆ e
2
i t
aˆ e f 0 e
2
0
i t
a ( i 2 ) f 0
2
2
0
37.
f0a 2
2
( 0 ) i 2
( ) i 2 e
2
0
2
( ) 4
2
0
2 2
2
2
arctg 2
2
0
i
2
38.
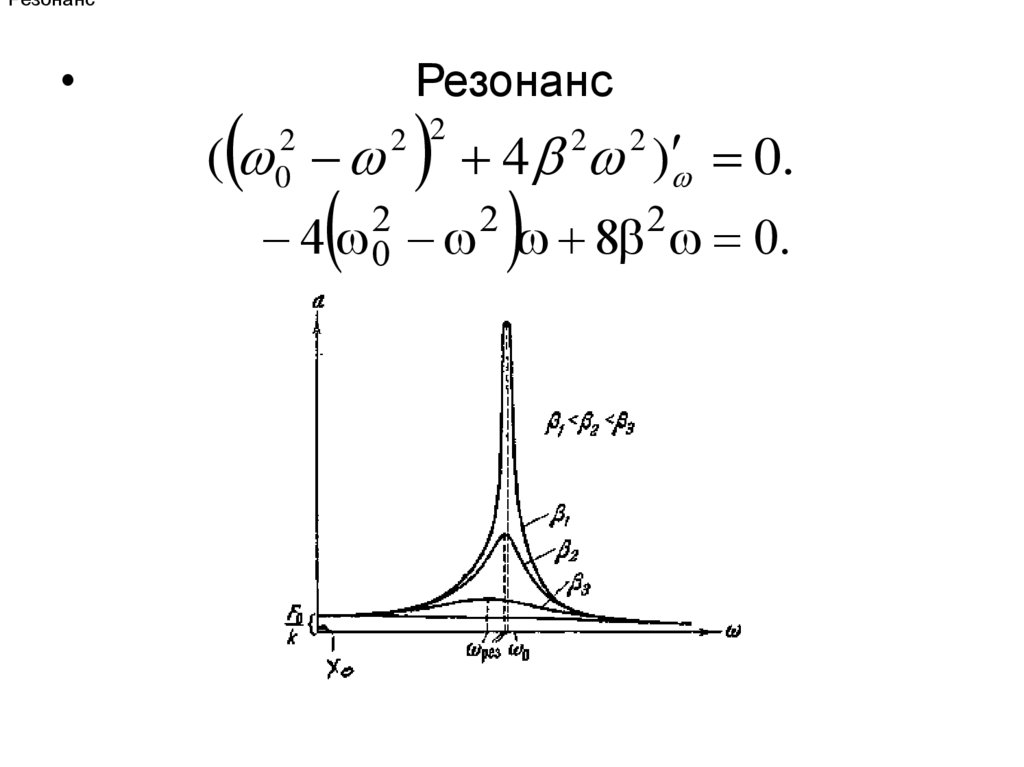
РезонансРезонанс
(
2
0
4 ) 0.
2 2
2
2
2
2
2
4 0 8 0.
39.
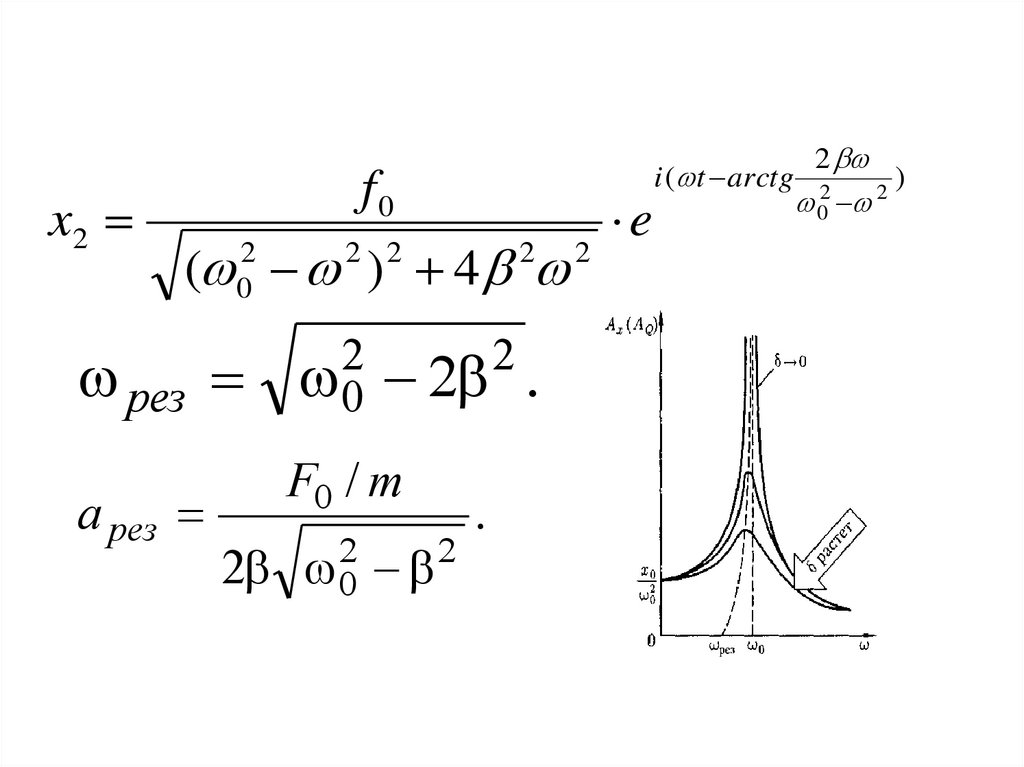
x2f0
( ) 4
2
0
рез
a рез
2 2
2
2
0 2 .
F0 / m
2
2
2
2
0
.
2
e
i ( t arctg
2
)
2
2
0
40.
Волновое уравнение. Фазовая и групповая скорости.
2 2 2
1 2
2 2 2 2
2
x
y
z
V t
1
2
2
V t
2
Уравнение плоской волны
( x, t ) Ae
i ( t kx 0 )
( x, t ) A cos( t kx 0 )
41.
Vфазов ое
k
2
T
k
2
dx d
Vгруппов ое
dt dk
Уравнение сферической волны
A0
( x, t )
cos( t kx 0 )
r
42.
• Физический и математический маятники.d ( J )
L [r F ]
dt
d
J
rF sin lmg sin lmg
dt
d
J lmg 0
dt
2
lmg
0 0
0
J
A cos( 0 t )
2
J
T
2
0
mgl
J ml
2
43.
Сложение взаимно перпендикулярных колебаний
x A cos( t )
x
cos( t )
A
y B cos( t )
y
cos( t ) cos t cos sin t sin
B
x 2 2 xy
y2
2
cos
sin
2
2
A
AB
B
= m
= (2m+1)
2
B
y ( ) x
A
2
2
x
y
2 1
2
A B
44.
Фигуры Лиссажу
45.
Фигура Лиссажу
46.
Волновое уравнение. Фазовая игрупповая скорости.
2 2 2
1 2
2 2 2 2
2
x
y
z
V t
( x, t ) Ae
Vфазов ое
k
i ( t kx 0 )
d
Vгруппов ое
dk
A0
( x, t )
cos( t kx 0 )
r
47.
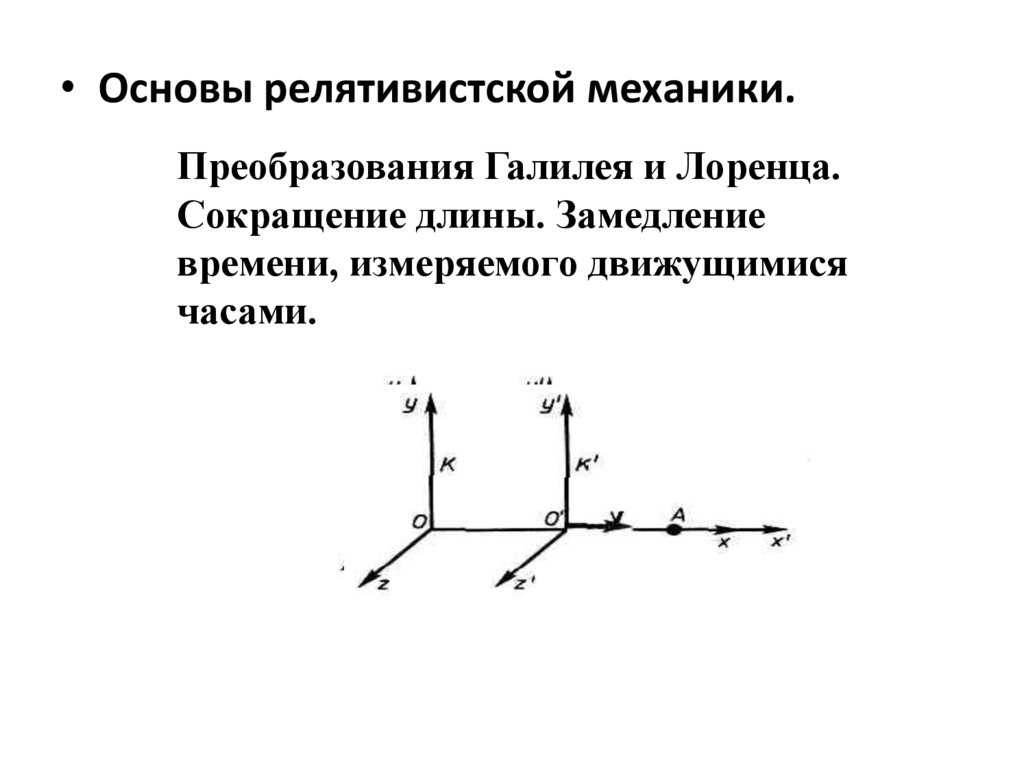
• Основы релятивистской механики.Преобразования Галилея и Лоренца.
Сокращение длины. Замедление
времени, измеряемого движущимися
часами.
48.
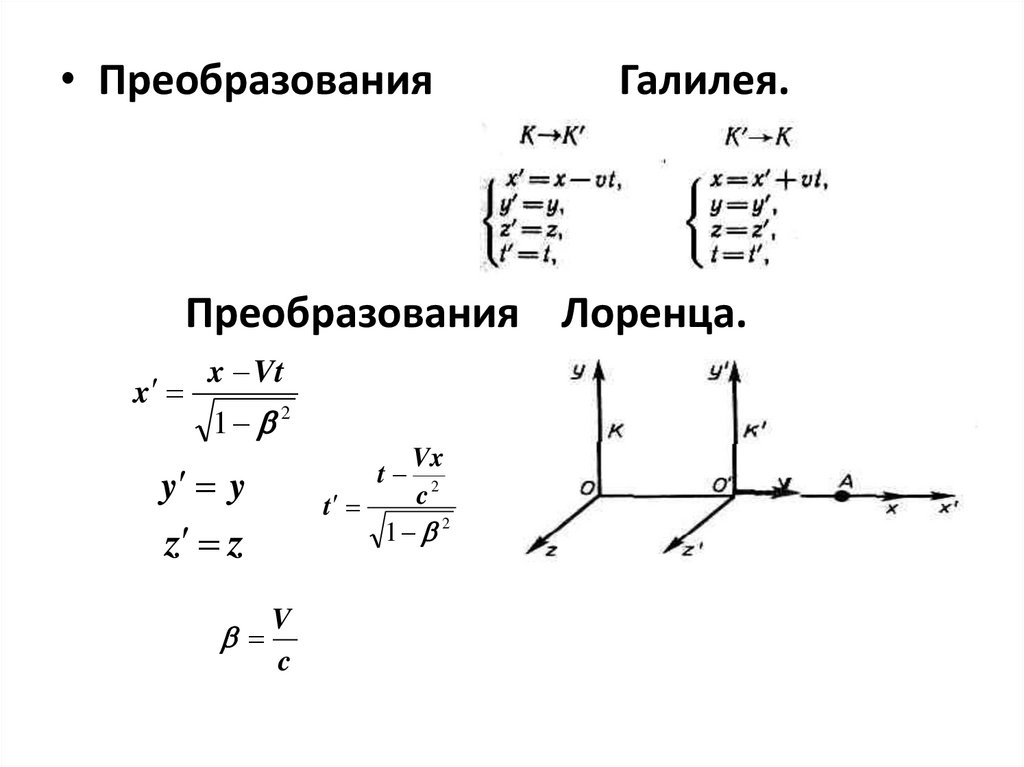
• ПреобразованияГалилея.
Преобразования Лоренца.
x
x Vt
1 2
Vx
2
c
t
1 2
t
y y
z z
V
c
49.
• Сокращение длины.l l0 1
2
Замедление времени.
0
1
2
50.
Релятивистский закон сложенияскоростей.
51.
Основной закон релятивистской динамикиматериальной точки
.
m
m0
V2
1 2
c
dP d (mV )
F
dt
dt
d
F (
dt
m0V
2
V
1 2
c
)
52.
Закон взаимосвязи массы и энергии.T (m m0 )c 2
T m0 c (
2
E c 2 m
E m0 c 2
1
V2
1 2
c
1
V2
1 2
c
1)
mc2
E m0 c T
2
E0 m0 c
2
53.
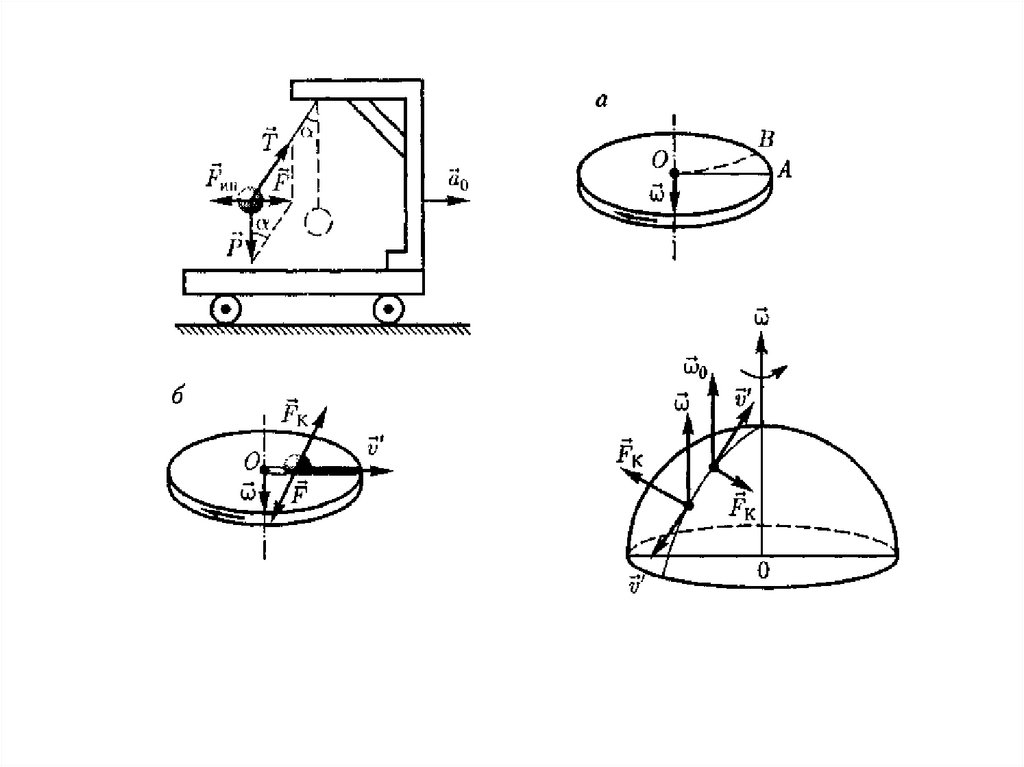
Движение в неинерциальныхсистемах отсчета.
dV
U
m
mW m[r ] 2m[V ] m[ [r ]].
dt
r
1.Потенциальная сила.
2.Сила инерции при поступательном
движении.
3.Сила возникает при увеличении угловой
скорости.
4.Кориолисово сила.
5. Центробежная сила.
54.
55.
• МОЛЕКУЛЯРНАЯ ФИЗИКАУравнение состояния. Основное уравнение
молекулярно –кинетической теории.
В молекулярно-кинетической теории пользуются
идеализированной моделью идеального газа,
согласно которой считают, что:
• 1) собственный объем молекул газа пренебрежимо
мал по сравнению с объемом сосуда;
• 2) между молекулами газа отсутствуют силы
взаимодействия;
• 3) столкновения молекул газа между собой и со
стенками сосуда абсолютно упругие.
56.
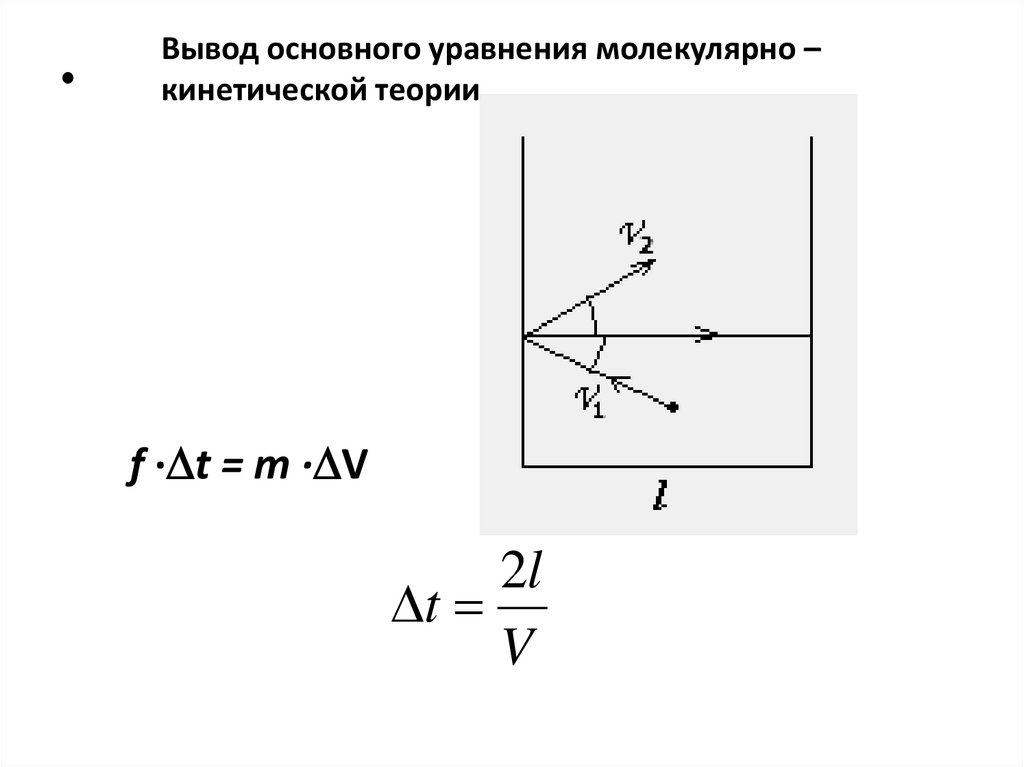
Вывод основного уравнения молекулярно –
кинетической теории.
f · t = m · V
2l
t
V
57.
• V = 2V; V = V2 – V12l
f m 2V
V
сила удара одной молекулы об стенку сосуда
mV
f
l
2
58.
• Вычислим силу удара об стенку сосуда N –молекул:
1
mN V12 V22 ... V 2 mN 2
F N f
V
3
3l
N
3l
F 2 m V
P 2 n
l
3
2
V2
2
Основное уравнение МКТ:
1
2
p mnV
3
59.
• Уравнение состояния или уравнениеМенделеева-Клапейрона:
pV
m
RT
mV 2 3
kT
2
2
p nkT
60.
Классическое распределение по скоростямМаксвелла
Справедливо для всех частиц:
dN Nf (V )dV1
dV1 4 V dV
2
dN Nf (V )4 V dV
2
dN
2
4 V f (V ) F (V )
NdV
61.
f (V ) (VX ) (VY ) (VZ )ln f (V ) ln (VX ) ln (VY ) ln (VZ )
1
df dV
1
d
f (V ) dV dVx (VX ) dVx
V V V V
2
x
2
y
dV V x
dV x V
2
z
62.
1d 1
1
df 1
f (V ) dV V (V x ) dV x V x
1
d 1
(V x ) dV x V x
d
V x dV x
63.
- условие нормировкиA e
V x2
2
Величина А (амплитуда вероятности) находится из
условия нормировки:
(
V
)
dV
1
x
x
A
2
m
kT
64.
f (V ) A e3
V
.
3
2
2
2
m
f (V )
e
2 kT
mV 2
2 kT
3
2
m
F (V ) 4 V
e
2 kT
2
mV 2
2 kT
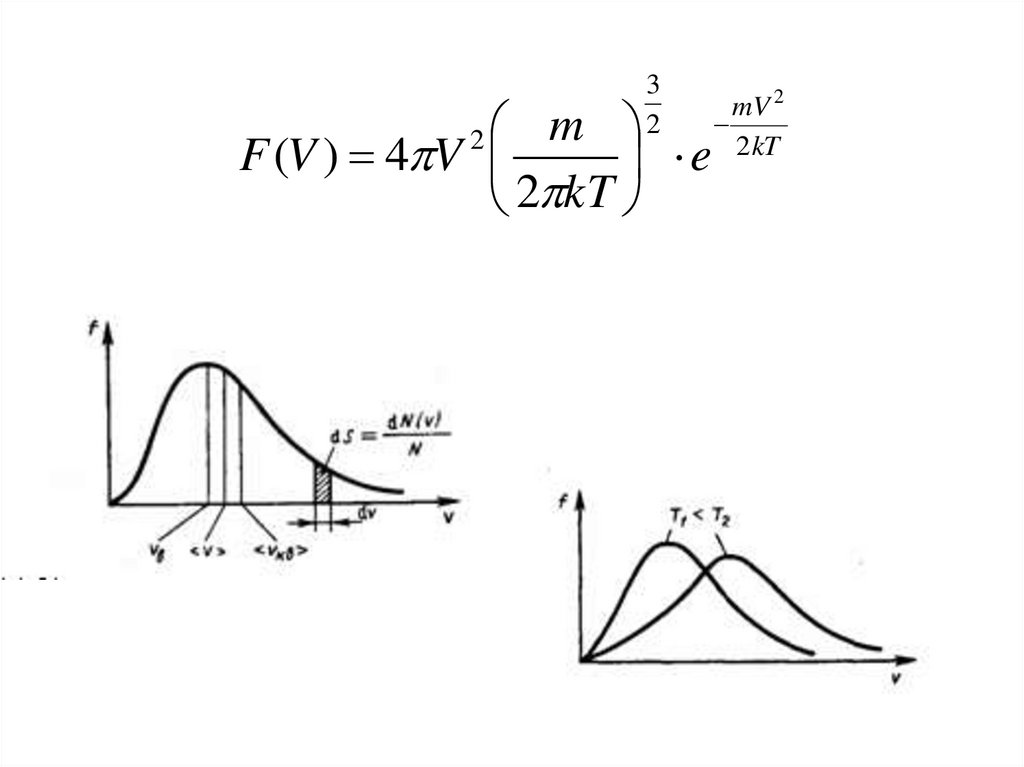
65.
32
m
F (V ) 4 V
e
2 kT
2
mV 2
2 kT
66.
• Барометрическая формула.p p0e
Mgh
RT
Распределение Больцмана.
n n0e
mgh
kT
67.
ТЕРМОДИНАМИКА
Первый закон термодинамики.
dQ dU dA
i
cm dT RdT pdVm
2
68.
dU m iRcVm
dT
2
c pm cVm R
i 2
c pm
R
2
i 2
cVm
i
c pm
i 3,5,6
69.
• Применение первого началатермодинамики к изопроцессам.
Изохорный процесс (V=const).
dA pdV 0
m
dQ dU
cV dT
M
Изобарный процесс (p=const).
m
A
R(T2 T1 )
M
70.
• Изотермический процесс (T=const).V2
V2
m
dV m
V2
A pdV RT
RT ln
M
V
M
V1
V1
V1
m
p1
или A
RT ln
M
p2
m
p1 m
V2
Q A
RT ln
RT ln
M
p2 M
V1
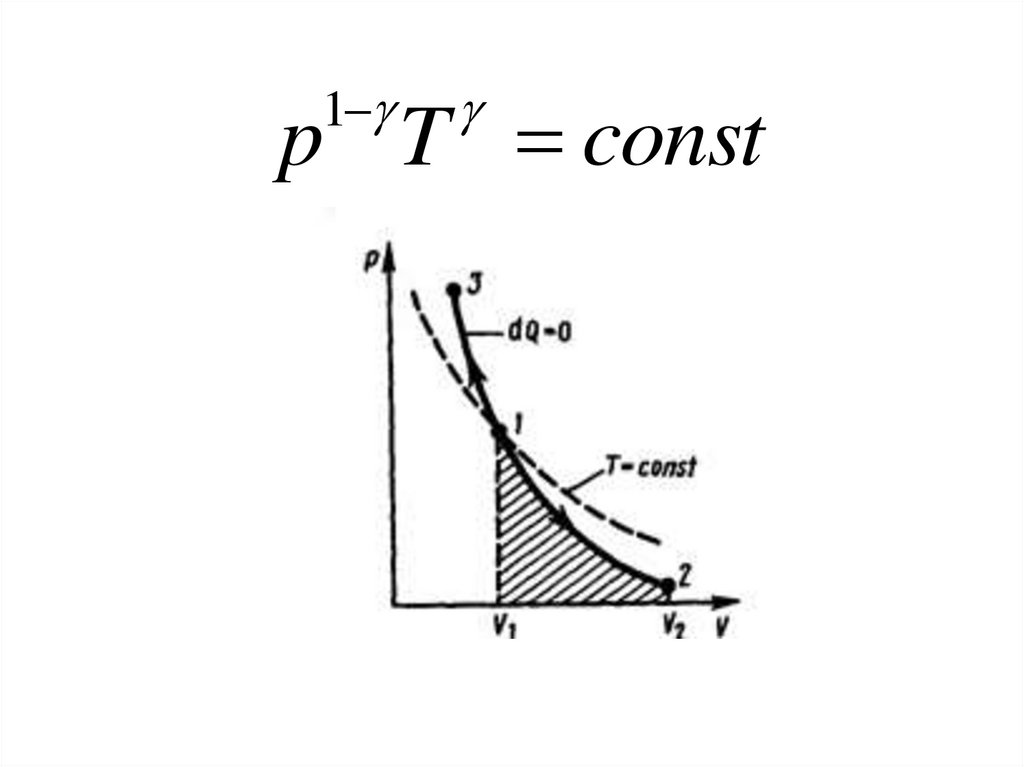
71.
• Адиабатический процесс.dQ 0
dA dU
m
pdV cV dT
M
m
pV
RT
M
Уравнения
Пуассона:
TV
1
const
pV const
72.
1p T const
73.
II закон термодинамики.• Энтропия замкнутой системы может либо
возрастать (в случае необратимых
процессов), либо оставаться постоянной
(в случае обратимых процессов).
Q
dU dA
S
T
T
1
1
2
2
74.
mdU
cV dT
M
m
dV
dA
RT
V2
T2
m
dV m
dT
M
V
S
R
cV
M V1 V M T1 T
Q
dU dA
S
T
T
1
1
2
2
m
V2
T2
S
( R ln cV ln )
M
V1
T1
75.
• при изотермическом процессе (T1=T2)m
V2
S
R ln
M
V1
при изохорном процессе (V1=V2)
m
T2
S
cV ln
M
T1
76.
Третье начало термодинамики(теорема Нернста — Планка):
Энтропия всех тел в состоянии равновесия
стремится к нулю по мере приближения
температуры к нулю Кельвина:
lim S 0
T 0
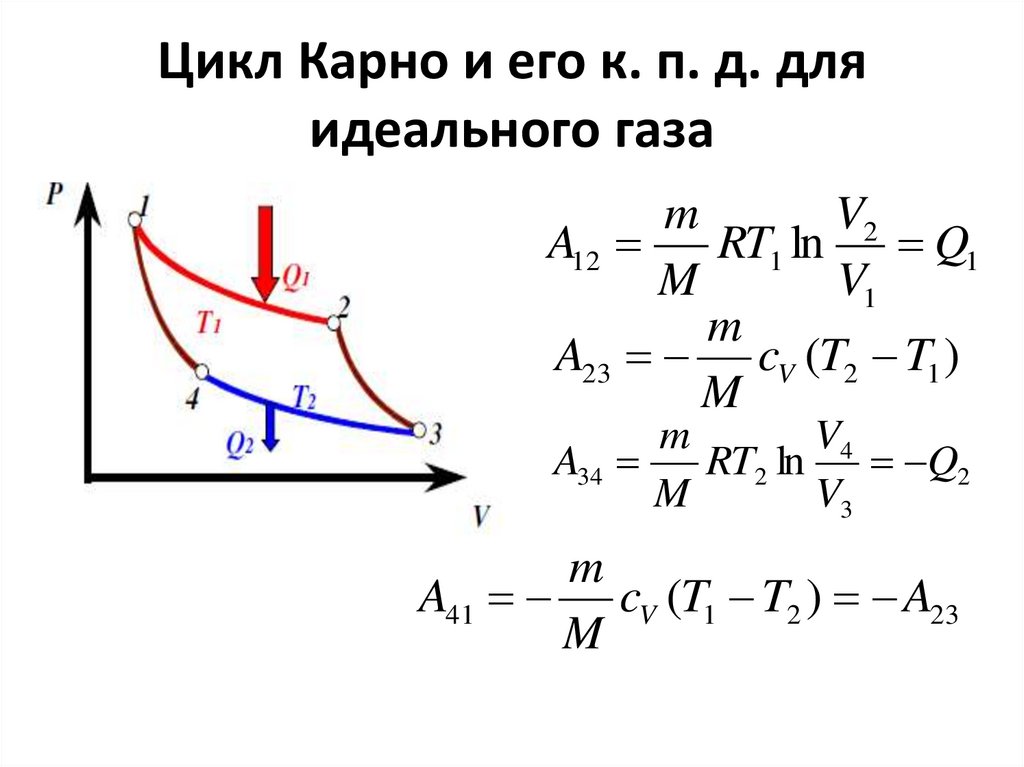
77.
Цикл Карно и его к. п. д. дляидеального газа
m
V2
A12
RT1 ln
Q1
M
V1
m
A23 cV (T2 T1 )
M
m
V4
A34
RT2 ln
Q2
M
V3
m
A41 cV (T1 T2 ) A23
M
78.
m
V2 m
V3
RT1 ln
RT2 ln
Q1 Q2 M
V1 M
V4
m
V2
Q1
RT1 ln
M
V1
Из уравнения Пуассона
TV 1 const
V2/V1 = V3/V4.
T1 T2
T1
79.
• Уравнение Ван-дер-ВаальсаДля реальных газов необходимо учитывать размеры
молекул и их взаимодействие друг с другом, поэтому
модель идеального газа и уравнение Клапейрона—
Менделеева.
pV RT
1. Учет собственного объема молекул.
не
V
a
V b
где b — объем, занимаемый самими
молекулами.
80.
• 2. Учет притяжения молекул.Приводит к появлению дополнительного
давления на газ, называемого внутренним
давлением.
a
p 2
V
a
( p 2 )(V b) RT
V
81.
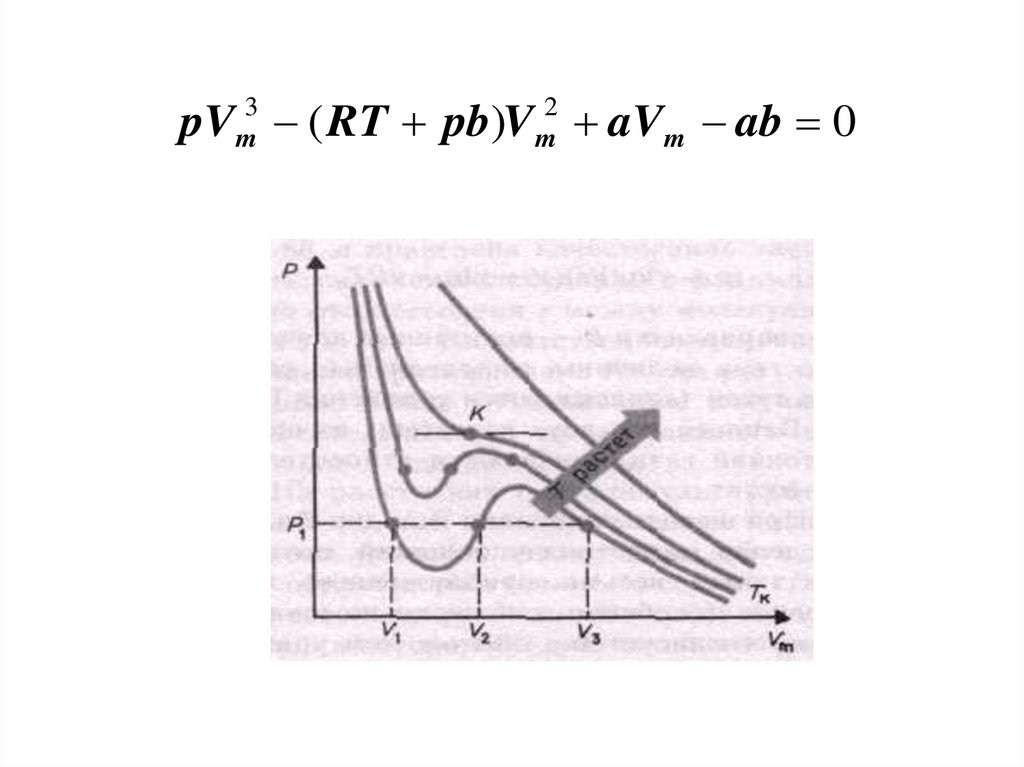
pV ( RT pb)V aVm ab 03
m
2
m
82.
• Для нахождения критических параметровнапишем
pkV 3 ( RTk pk b)V 2 aV ab 0
Поскольку в критической точке все три корня совпадают и
равны Vк, уравнение приводится к виду
p k (V V k ) 0
3
pkV 3 pkVkV 3 pkV V pkVk 0
3
pkVk3 ab
2
3 pkVk2 a
2
k
3
3 pkVk RTk pk b
83.
Vk 3ba
pk
27b 2
8a
Tk
27 Rb
84.
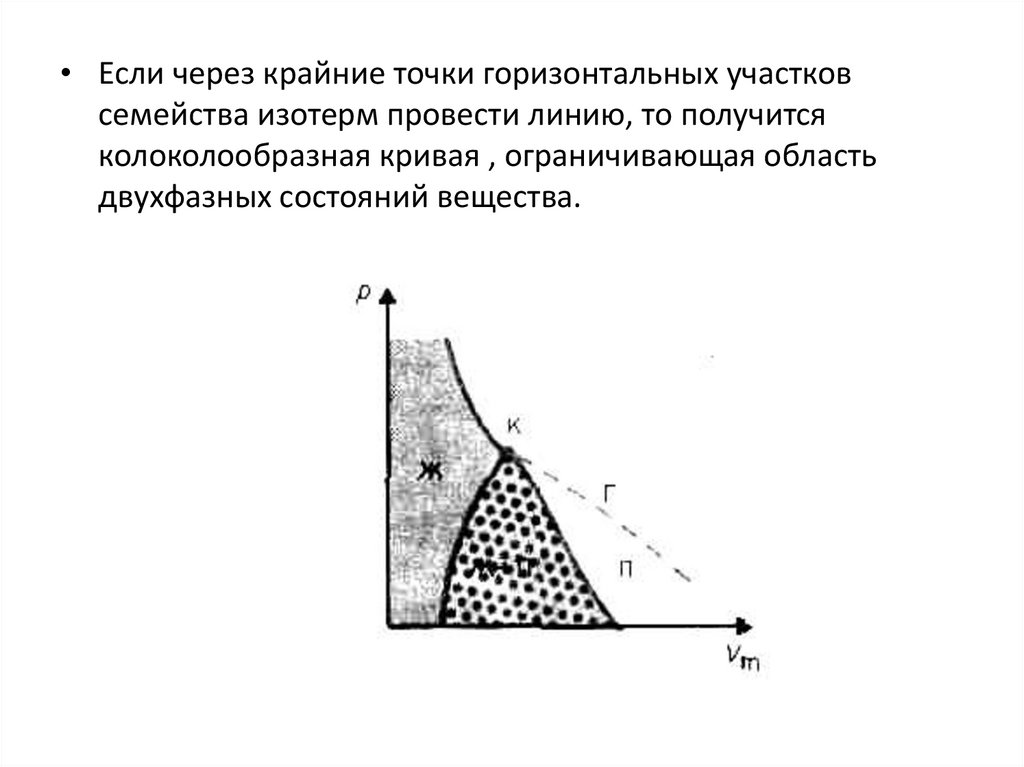
• Если через крайние точки горизонтальных участковсемейства изотерм провести линию, то получится
колоколообразная кривая , ограничивающая область
двухфазных состояний вещества.
85.
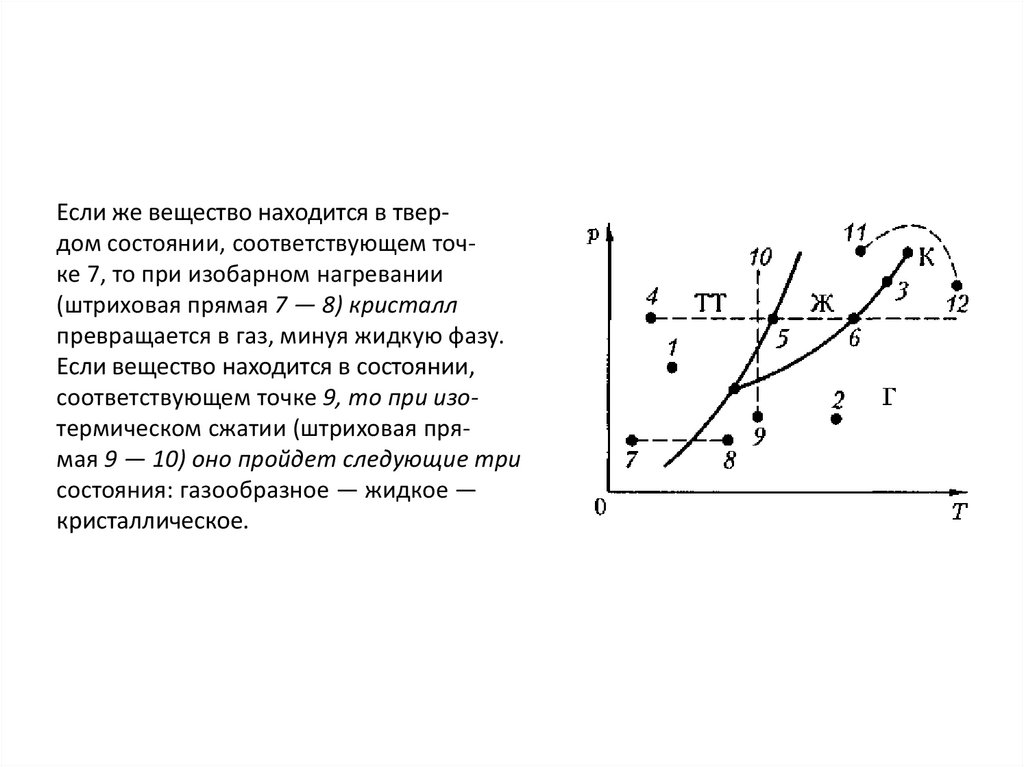
Если же вещество находится в твердом состоянии, соответствующем точке 7, то при изобарном нагревании(штриховая прямая 7 — 8) кристалл
превращается в газ, минуя жидкую фазу.
Если вещество находится в состоянии,
соответствующем точке 9, то при изотермическом сжатии (штриховая прямая 9 — 10) оно пройдет следующие три
состояния: газообразное — жидкое —
кристаллическое.
86.
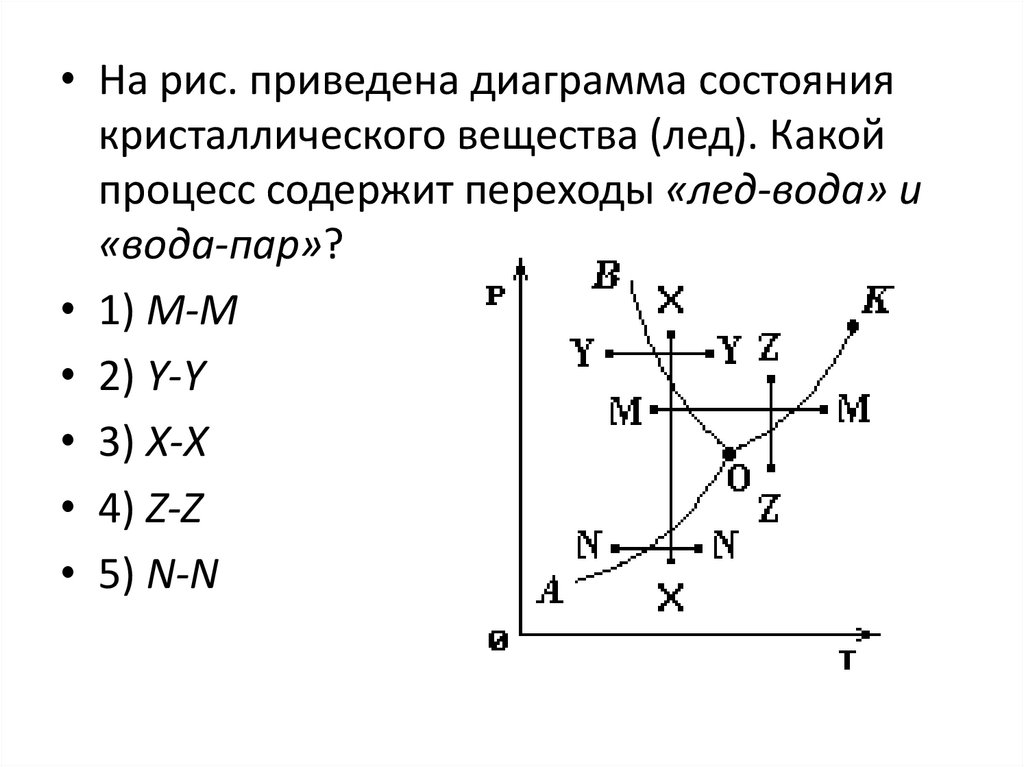
• На рис. приведена диаграмма состояниякристаллического вещества (лед). Какой
процесс содержит переходы «лед-вода» и
«вода-пар»?
• 1) М-М
• 2) Y-Y
• 3) X-X
• 4) Z-Z
• 5) N-N
87.
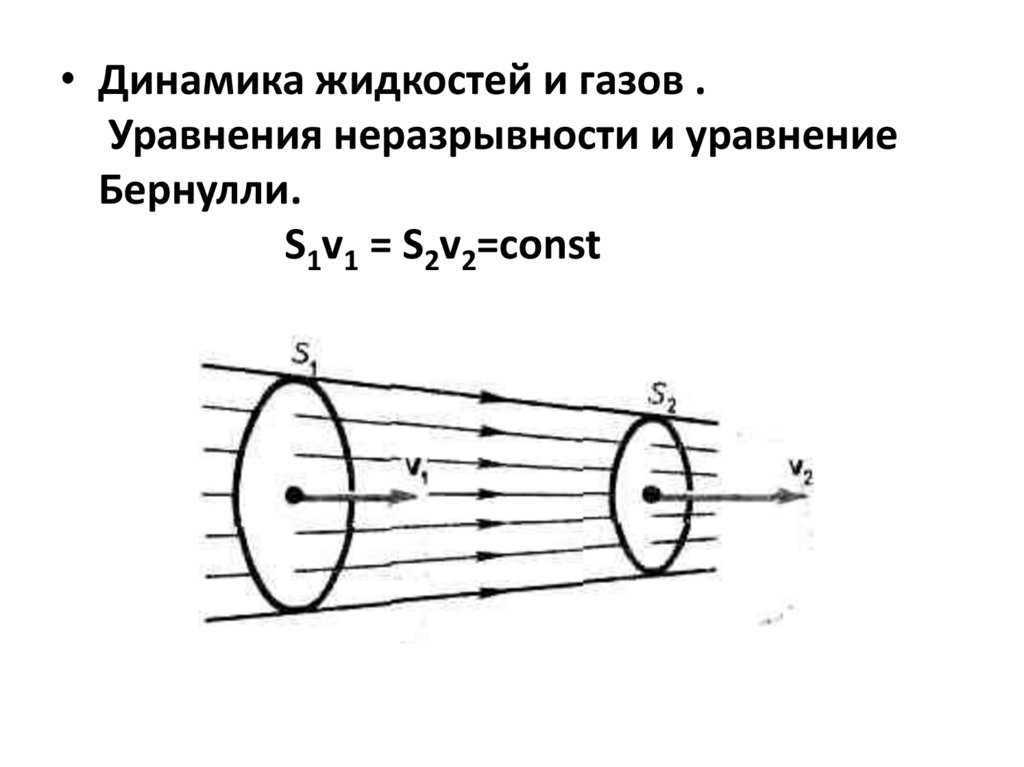
• Динамика жидкостей и газов .Уравнения неразрывности и уравнение
Бернулли.
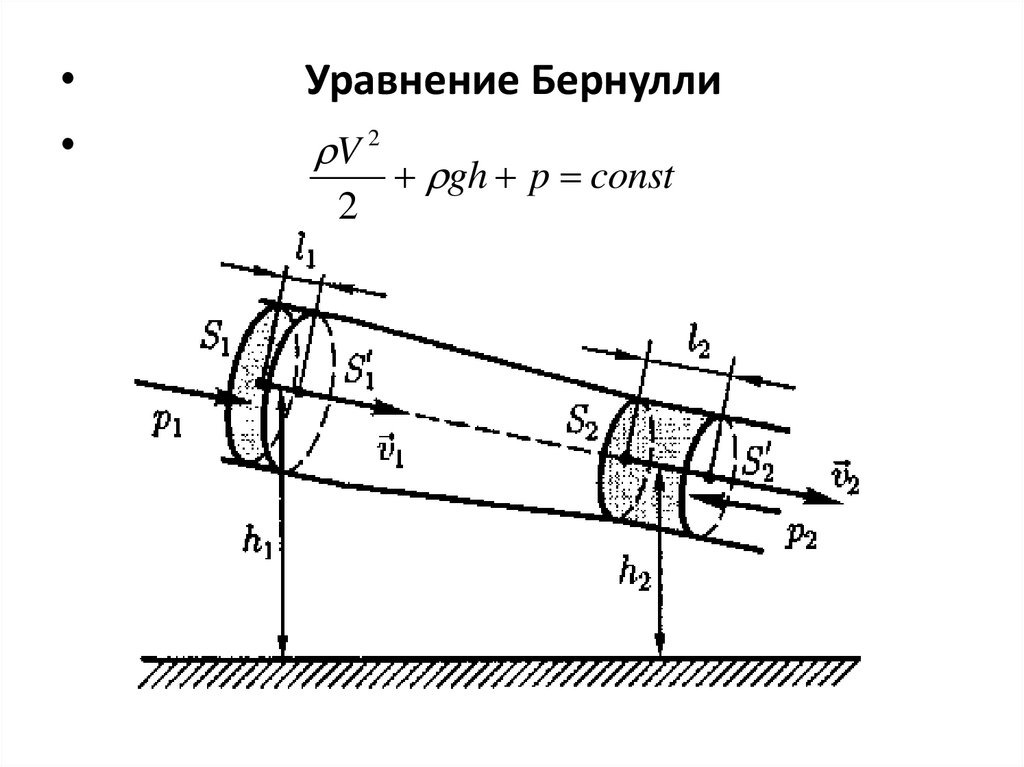
S1v1 = S2v2=const
88.
Уравнение Бернулли
V 2
2
gh p const
89.
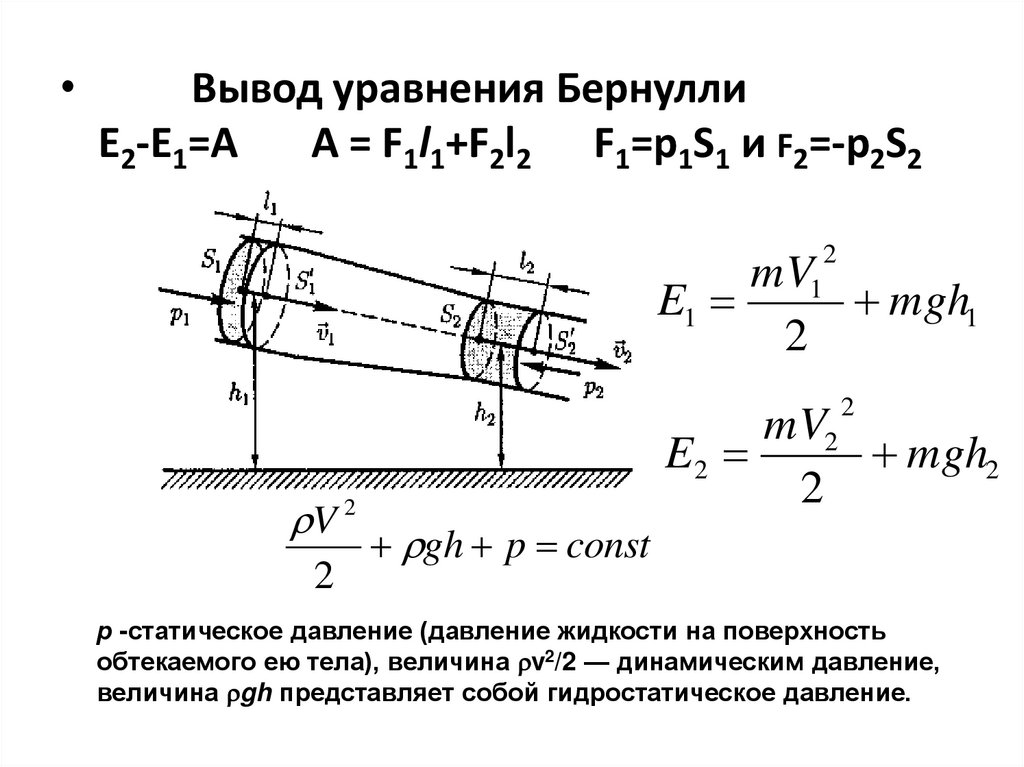
Вывод уравнения Бернулли
E2-E1=A
A = F1l1+F2l2 F1=p1S1 и F2=-р2S2
2
mV1
E1
mgh1
2
2
V 2
2
mV2
E2
mgh2
2
gh p const
р -статическое давление (давление жидкости на поверхность
обтекаемого ею тела), величина v2/2 — динамическим давление,
величина gh представляет собой гидростатическое давление.
90.
• Динамика жидкостей и газов .Истечение жидкости из отверстия. Формула Торричелли.
Рассмотрим два сечения
(на уровне h1 свободной
поверхности жидкости в сосуде и
на уровне h2 выхода ее из
отверстия). Напишем для них
уравнение Бернулли:
V12
2
gh1 p1
V22
2
gh2 p2
Так как давления р1 и р2 в жидкости на уровнях
первого и второго сечений равны атмосферному,
т. е. p1=p2, то уравнение будет иметь вид
91.
2
V1
V22
gh1
gh2
2
2
Из уравнения неразрывности S1v1 = S2v2=const
следует, что v2/v1=S1/S2, где S1 и S2 — площади поперечных сечений
сосуда и отверстия. Если S1>>S2, то членом v21/2 можно пренебречь и
V22 2 g (h1 h2 ) 2 gh
V2 2 gh
Это формула Торричелли
92.
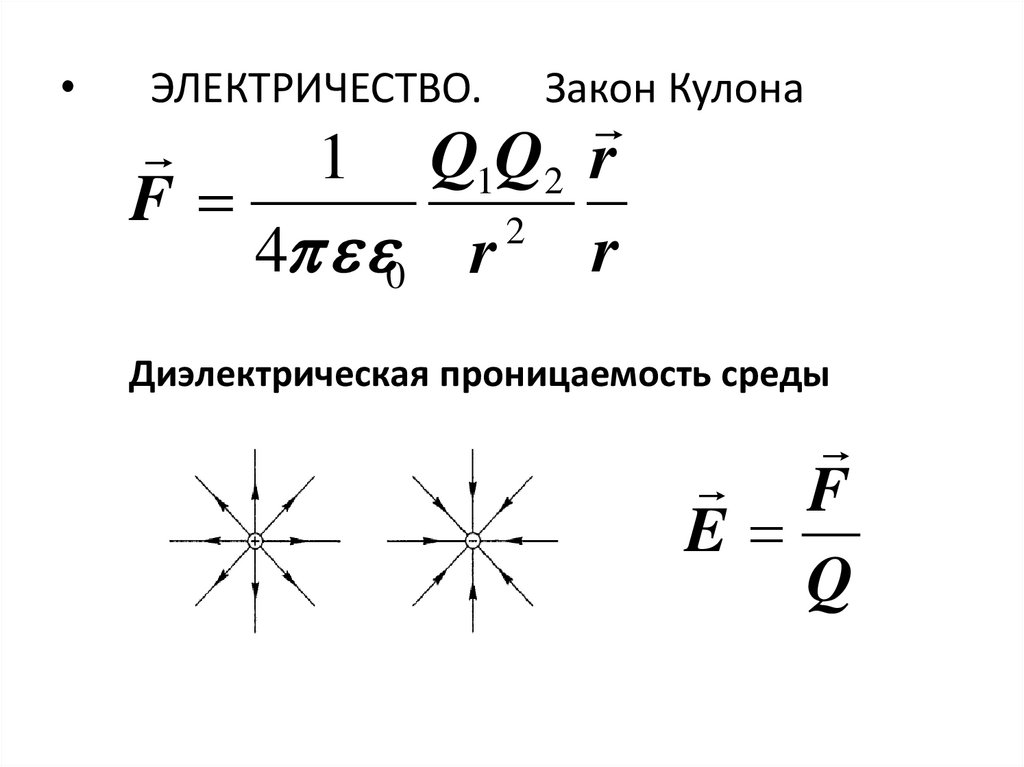
ЭЛЕКТРИЧЕСТВО.
Закон Кулона
1 Q1Q2 r
F
2
4 0 r r
Диэлектрическая проницаемость среды
F
E
Q
93.
1 QrE
2
4 0 r r
Ф EdS
S
94.
D 0 E95.
Электрический
диполь
p Ql
96.
• ПОЛЕ ДИПОЛЯE A E E
97.
98.
99.
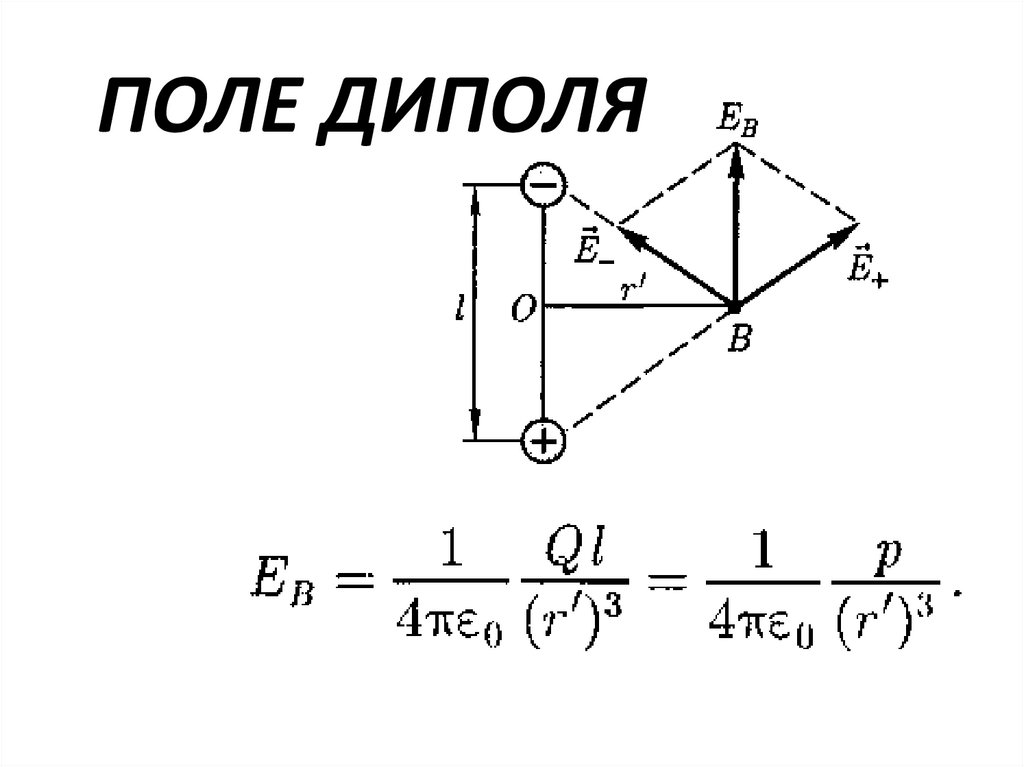
ПОЛЕ ДИПОЛЯ100.
Магнитный поток.Теорема Гаусса.
Ф EdS E dS
S
E S cos
Q
4 0 r
4 r
2
2
Q
0
1
Q
Ф EdS dV
0 V
S
n
D
d
S
Q
i
S
1
0
101.
102.
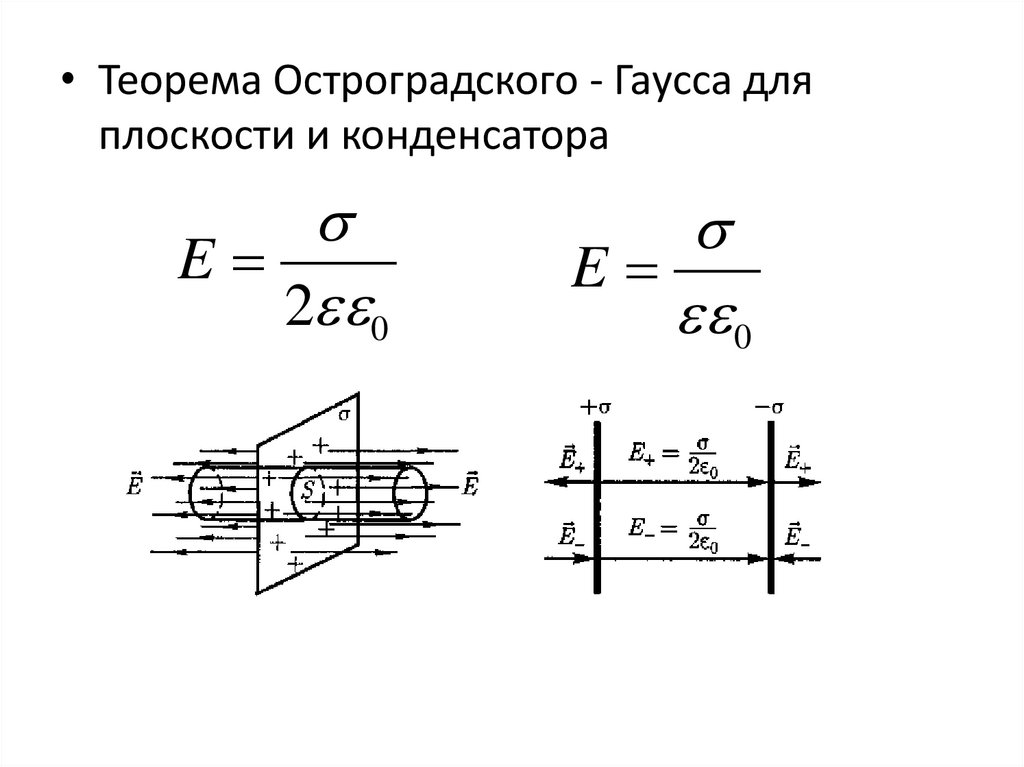
• Теорема Остроградского - Гаусса дляплоскости и конденсатора
E
2 0
E
0
103.
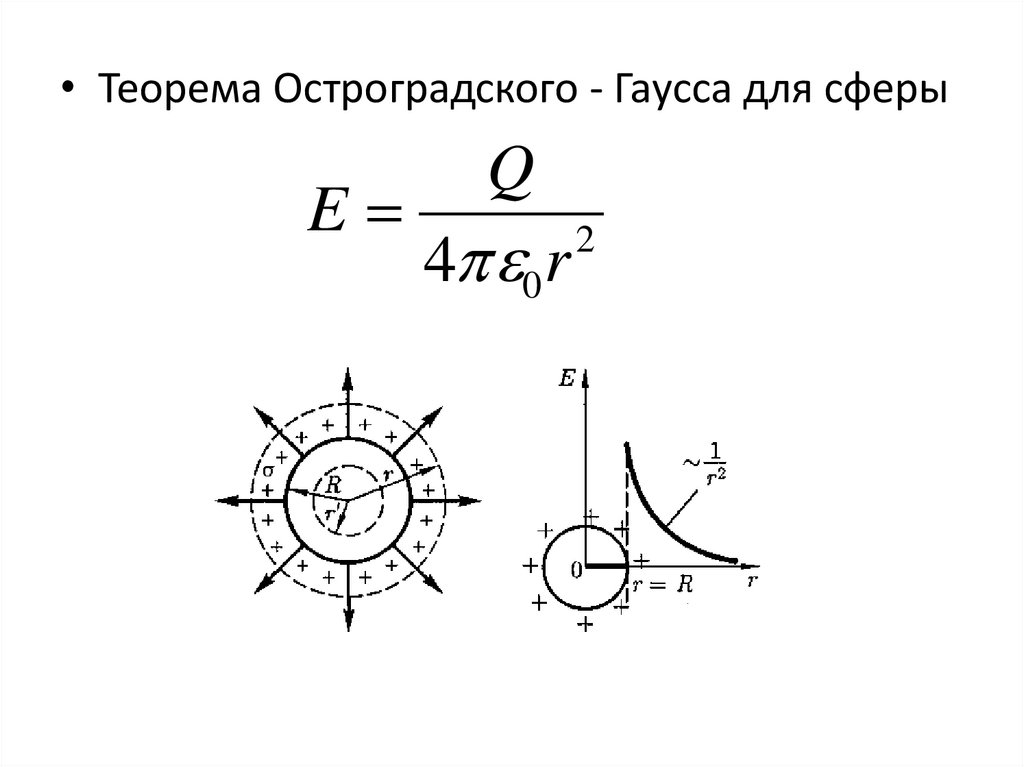
• Теорема Остроградского - Гаусса для сферыE
Q
4 0 r
2
104.
• Теорема Остроградского - Гаусса для шараQ
4 3
4 r E
r / 0
0 3
Q
r
E
4 3
3 0
R
3
Qr
E
3
4 0 R
2
105.
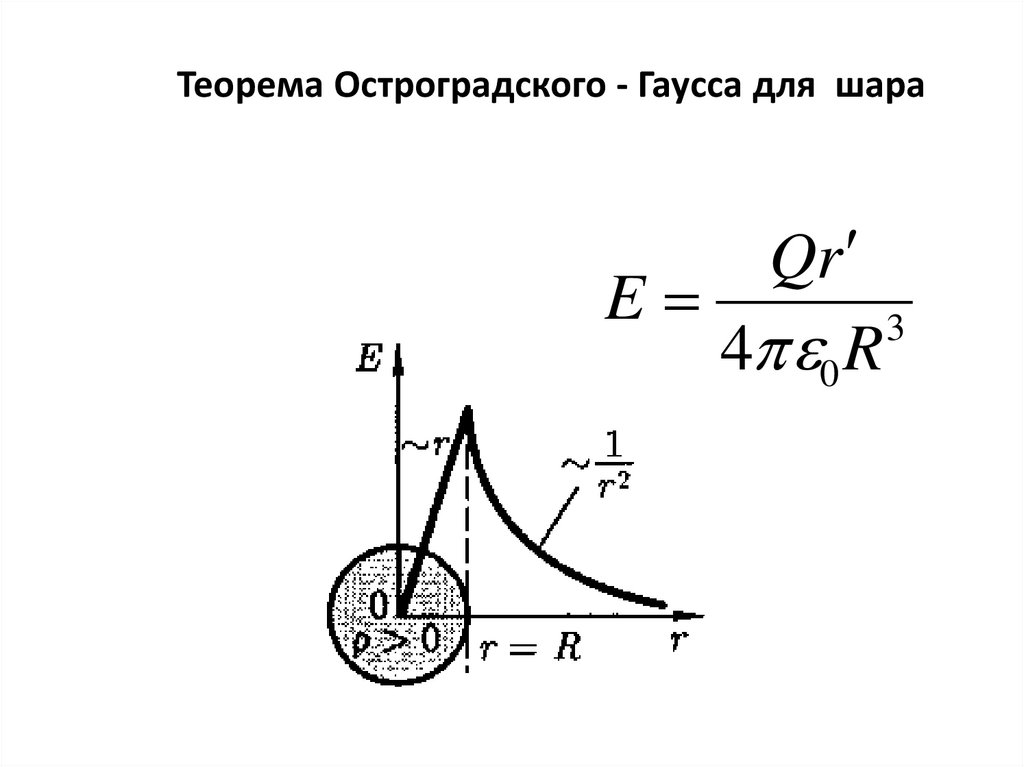
Теорема Остроградского - Гаусса для шараQr
E
3
4 0 R
106.
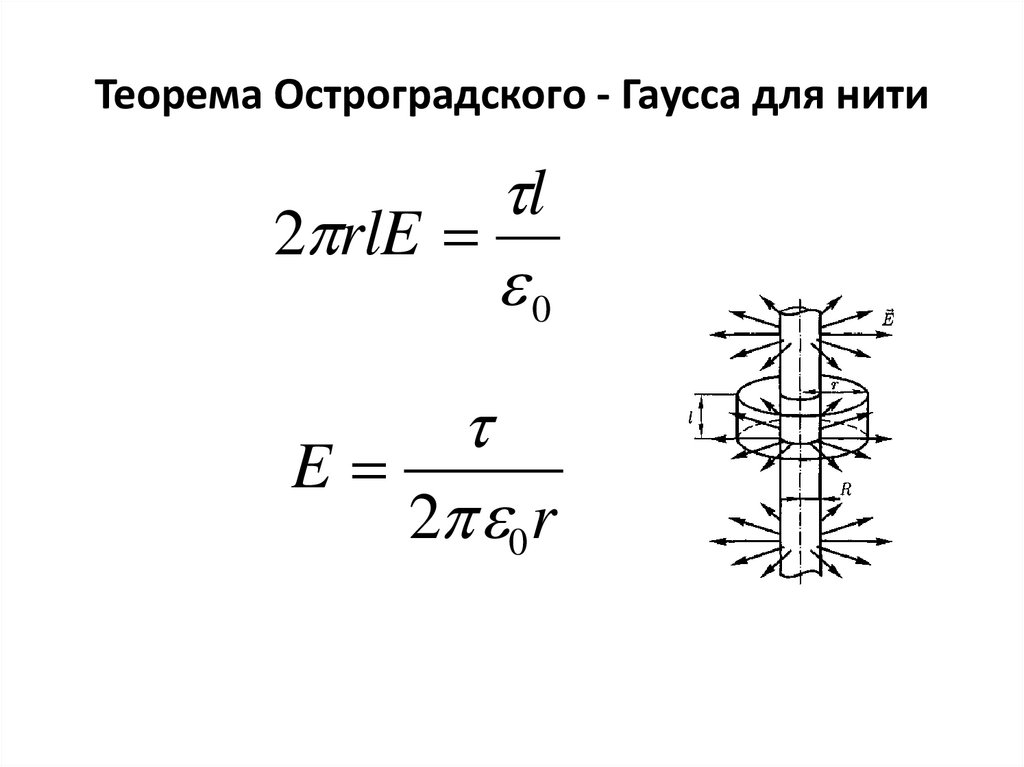
Теорема Остроградского - Гаусса для нитиl
2 rlE
0
E
2 0 r
107.
Потенциал электрического поляE grad
d
E
dr
E dr
108.
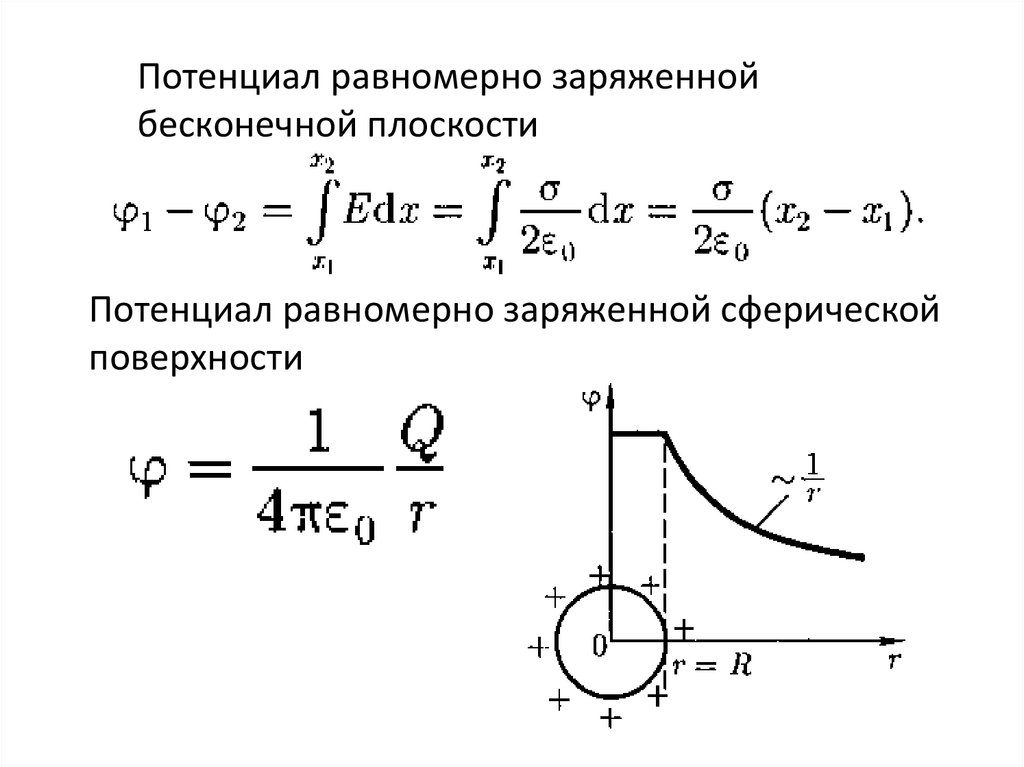
Потенциал равномерно заряженнойбесконечной плоскости
Потенциал равномерно заряженной сферической
поверхности
109.
• Потенциал точечного зарядаПотенциал объемно заряженного шара
R ( R r )
3 0
6 0
2
2
2
110.
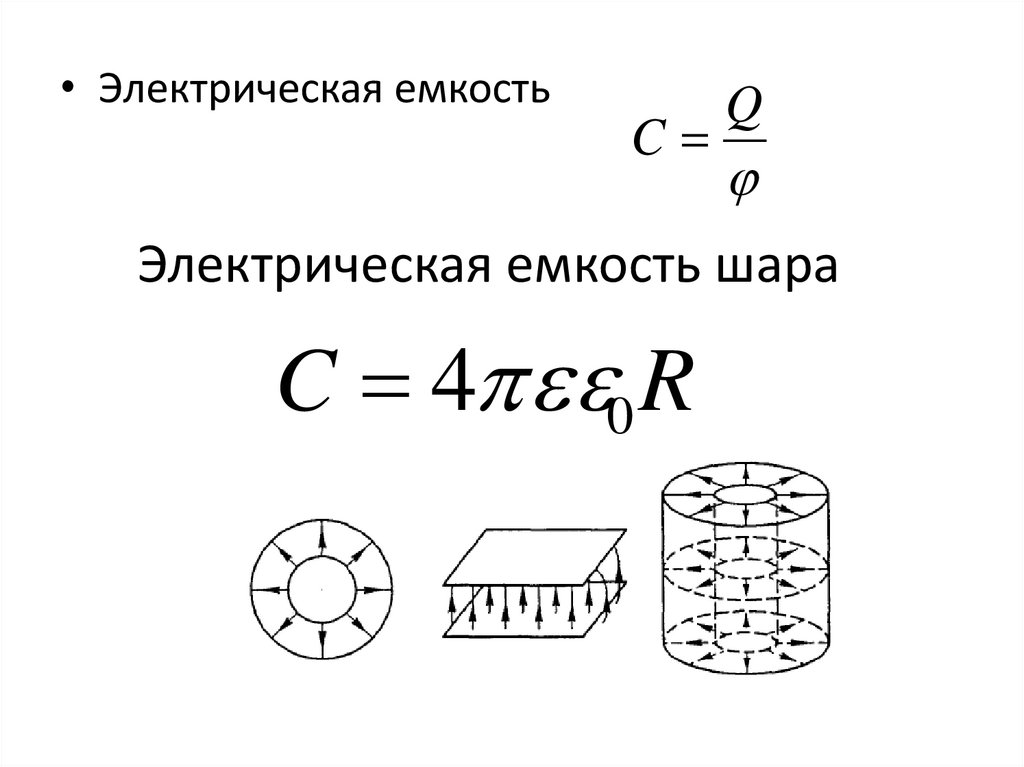
• Электрическая емкостьC
Q
Электрическая емкость шара
C 4 0 R
111.
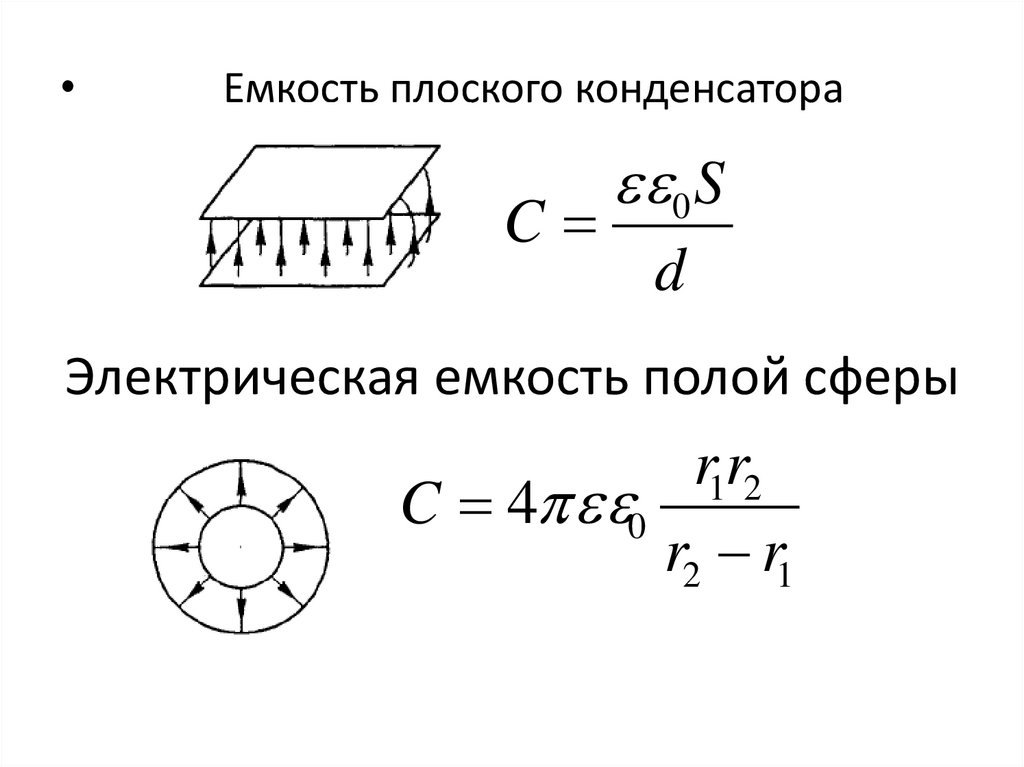
Емкость плоского конденсатора
0 S
C
d
Электрическая емкость полой сферы
r1r2
C 4 0
r2 r1
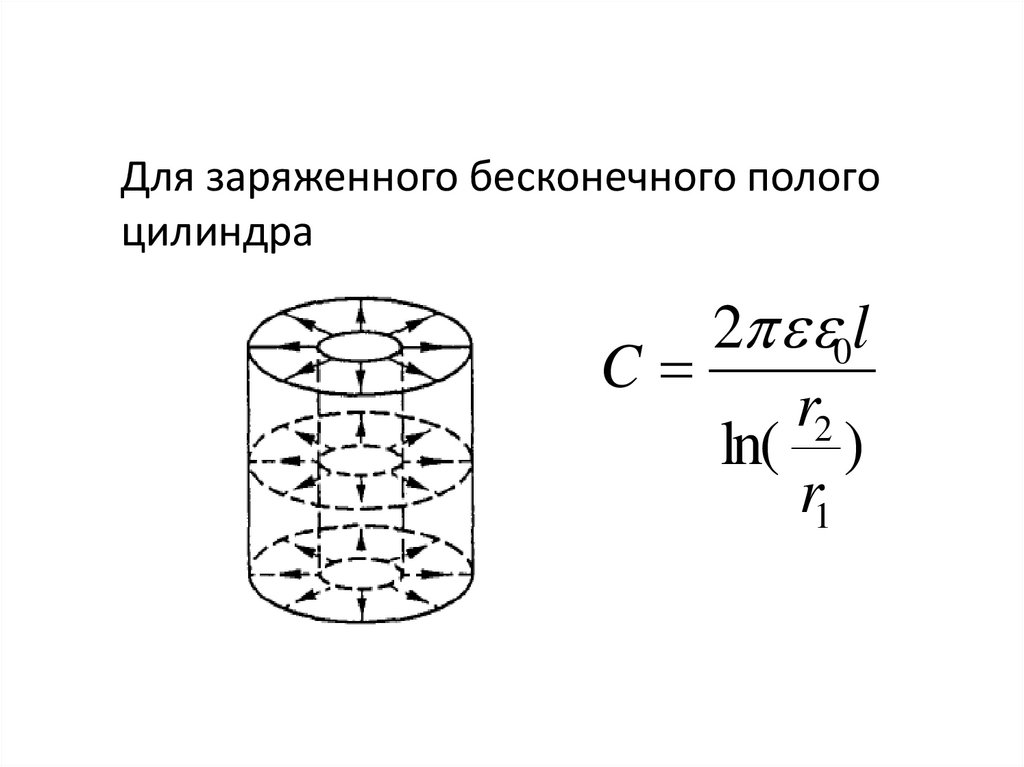
112.
Для заряженного бесконечного пологоцилиндра
2 0l
C
r2
ln( )
r1
113.
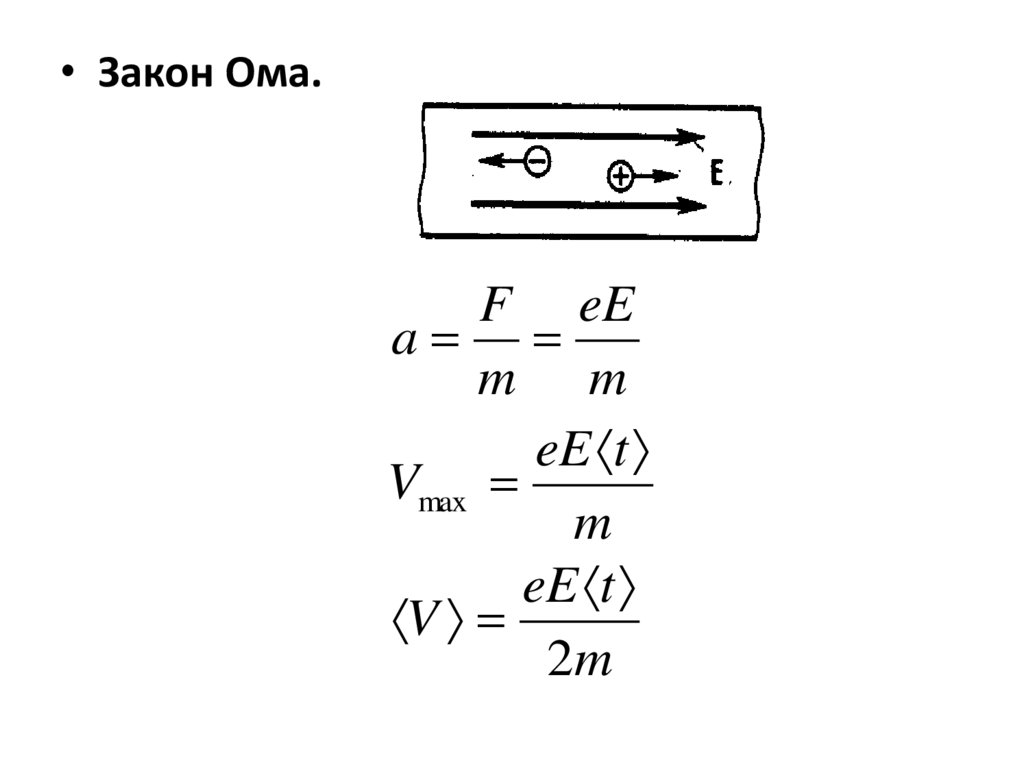
• Закон Ома.F eE
a
m m
eE t
Vmax
m
eE t
V
2m
114.
l
t
u
eE l
V
2m u
ne E l
j ne V
2m u
2
Закон Ома в дифференциальной форме
j E
ne l
2 m u
2
115.
• Закон Джоуля — Ленца. К концу свободногопробега электрон под действием поля приобретает
дополнительную кинетическую энергию
2
max
mV
Ek
2
e E l
2
2m u
2
2
2
За единицу времени электрон испытывает с узлами
решетки в среднем z столкновений:
u
Z
l
116.
• Если n — концентрация электронов, то в единицувремени происходит п z столкновений и решетке
передается энергия
W n Z Ek
энергия, передаваемая решетке в единице объема
проводника за единицу времени,
ne E l
W
2m u
2
2
117.
• Закон Видемана — Франца.Отношение теплопроводности к удельной
проводимости для всех металлов при одной и той же
температуре одинаково и увеличивается
пропорционально термодинамической температуре:
T
=3(k/e)2
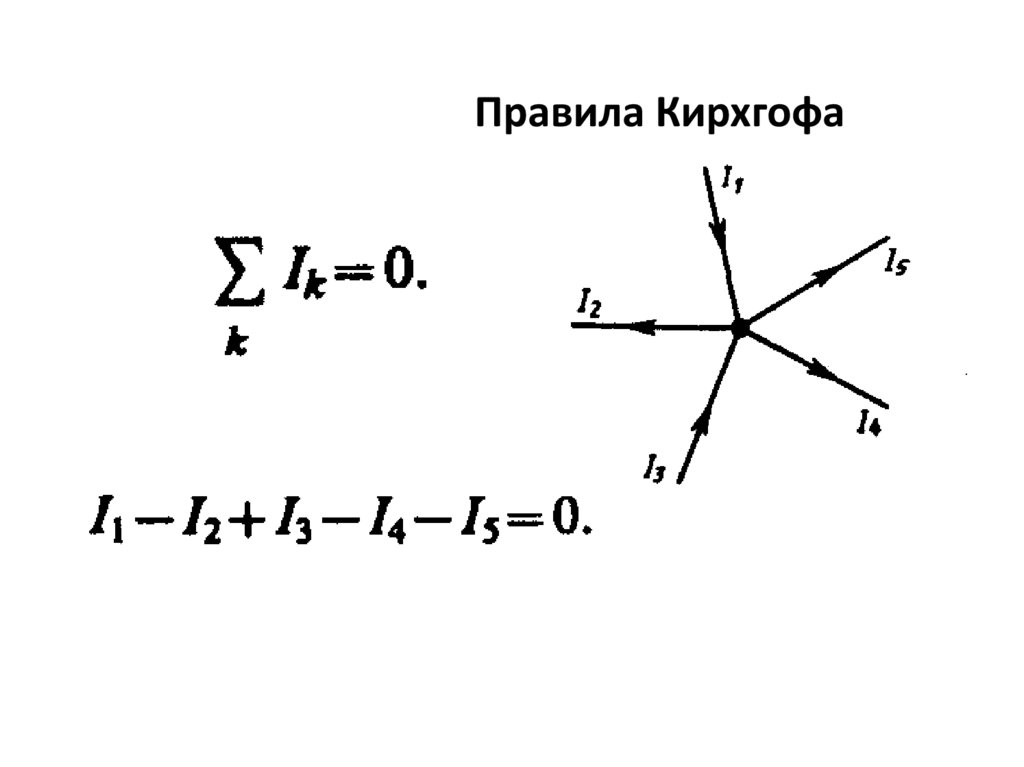
118.
Правила Кирхгофа119.
120.
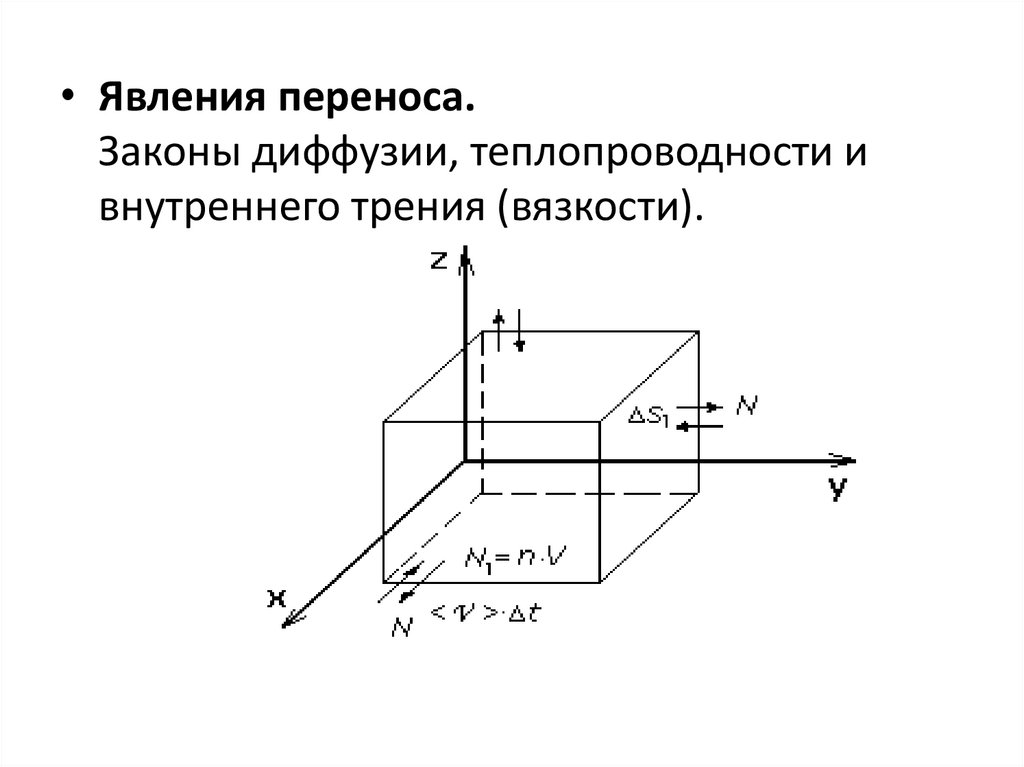
• Явления переноса.Законы диффузии, теплопроводности и
внутреннего трения (вязкости).
121.
• Основное уравнение явления переноса:1 ( n )
( N )
2 V t S
6 x
Диффузия
= m;
1
M
V S t
3 x
1
D V
3
122.
;
•Теплопроводность
i
kT
2
уравнение теплопроводности (уравнение Фурье).
1
T
Q CV V S t
3
x
1
СV V
3
123.
Внутреннее трение
= p = mV
1 V
F
V S
3 x
уравнение трения (уравнение Ньютона).
124.
• Движение в центральном поле.m 2 2 2
E (r r ) U (r )
2
2
M m r
2
r r E U (r )
m
2
2
2
125.
M2
mr
2
2 2
r E U (r ) r
m
2
2
2
M
r E U (r ) 2 2
m
m r
2
126.
2r
M
2[ E U (r )]
2
mr
m
dt
dr
2
2
M
E U (r ) 2 2
m
m r
127.
Md
dt
2
mr
d
M
dr
2
mr
2
2
M
E U (r ) 2 2
m
m r
128.
Mdr
2
mr
2
2
M
E U (r ) 2 2
m
m r
U (r )
r
C
129.
Mdr
2
mr
C
2
2
M
E 2 2
m
r m r
dr
r2
2m
1
E 2
2
M
r r
dr
r2
2mE 2m 1
2 2
2
M
M r r
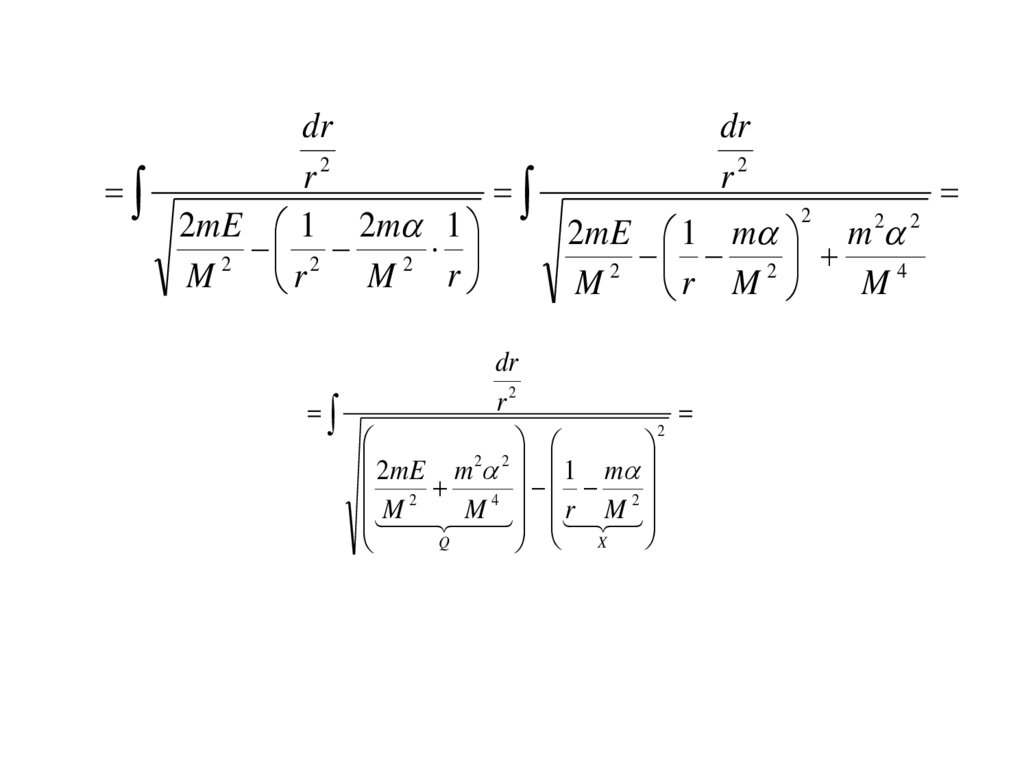
130.
drdr
2
r2
r
2
2 2
2mE 1 2m 1
2
mE
1
m
m
2
2
M 2 r2 M 2 r
M
M4
r M
dr
r2
2
2mE m 2 2 1 m
2
2
4
M
M
r M
Q
X
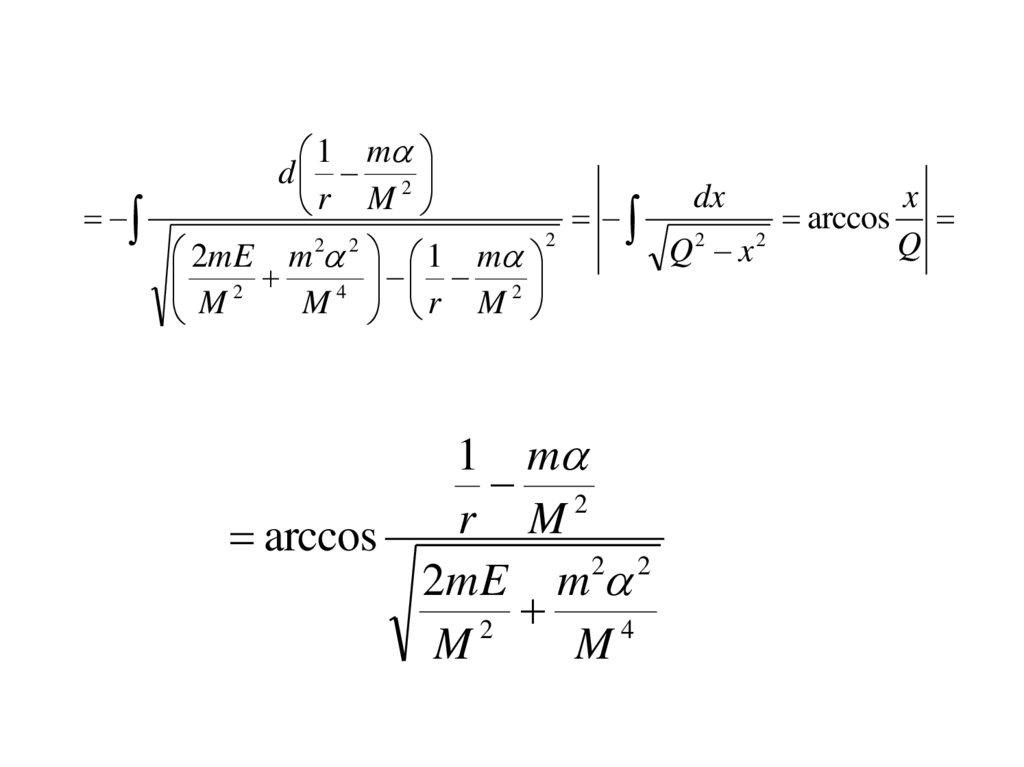
131.
1 md 2
r M
2mE m 2 2 1 m
2
2
4
M r M
M
2
1 m
2
r M
arccos
2 2
2mE m
2
M
M4
dx
x
arccos
2
2
Q
Q x
132.
M1 m
2
m
r M
2
2 2
M
2mE m
2
4
m
M
M
2
cos
2
2
M 1
M 1
1
1
m r
m r
4
2
2mE M
2M E
2 2 1
1
2
2
M
m
m
133.
2M
p
• m
2
2M E
1
e
2
m
эксцентриситет
p
r
1 e cos
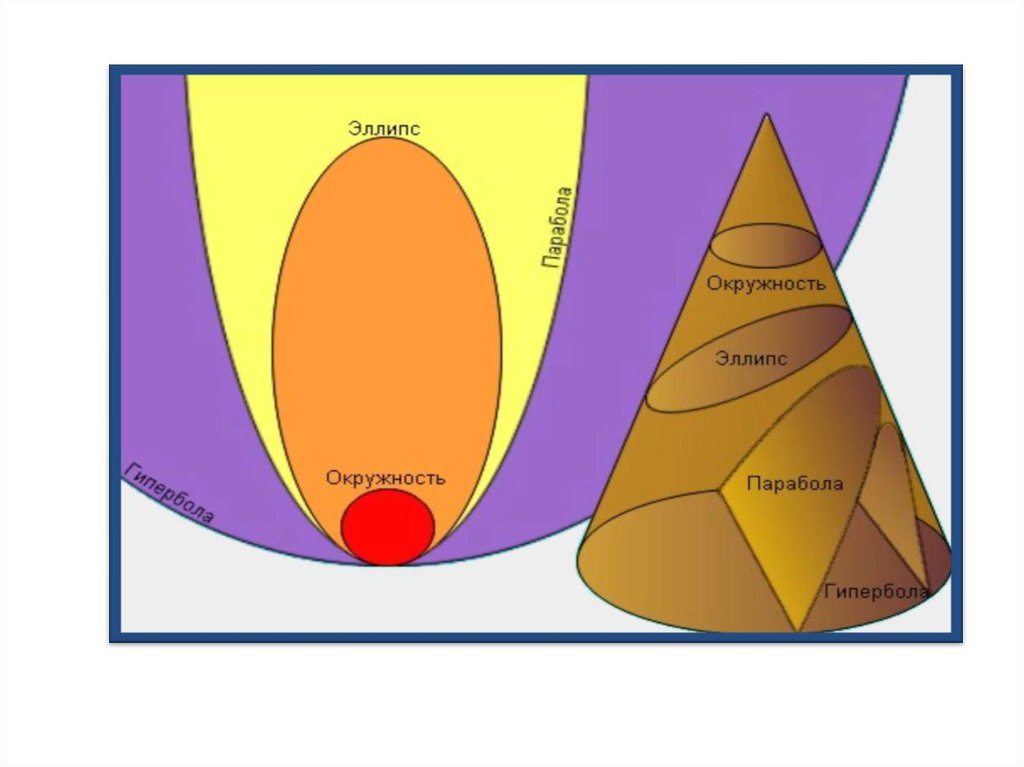
e 1 эллипс, e 0 окружность, e 1 парабола
уравнение конического сечения.


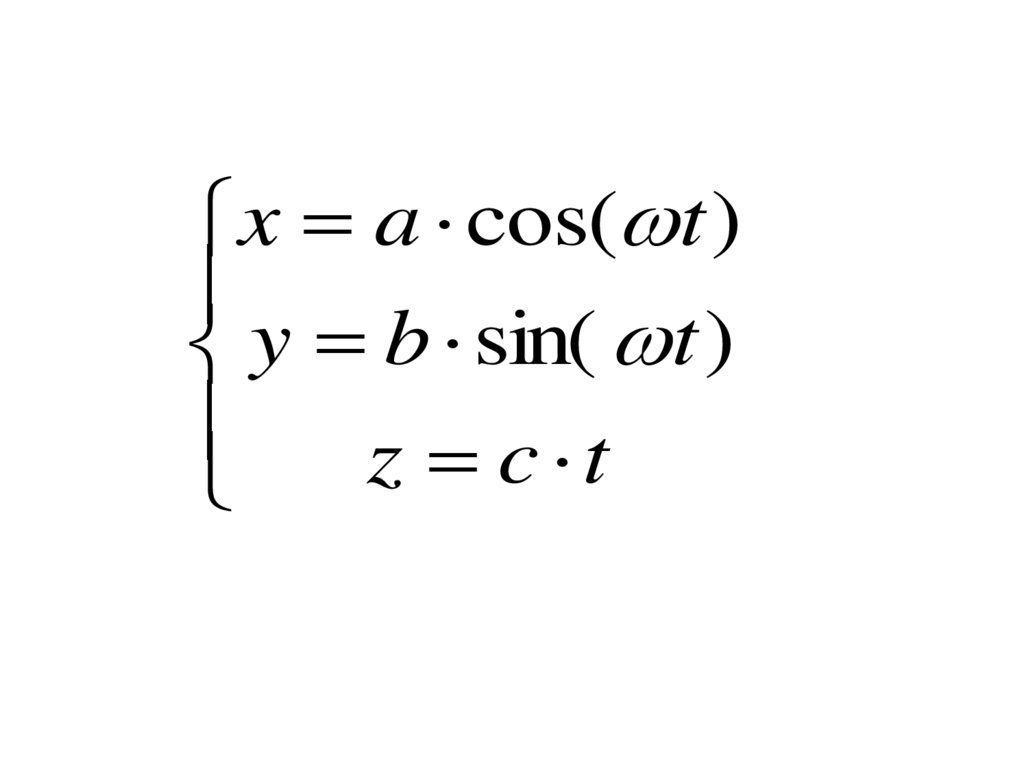


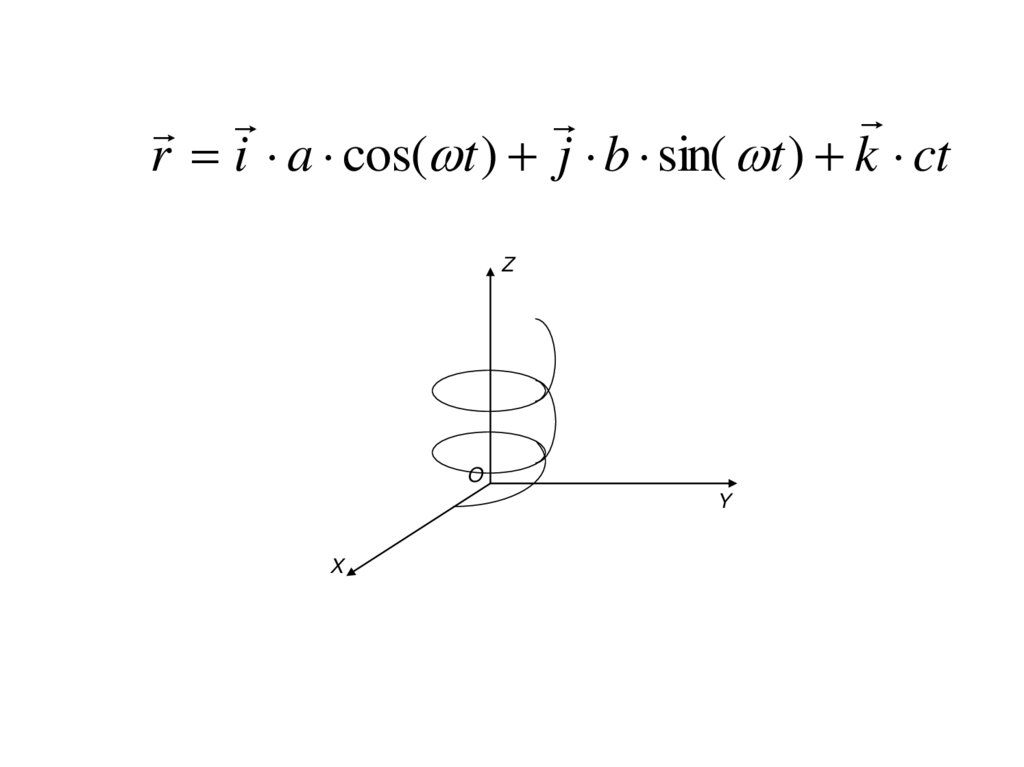
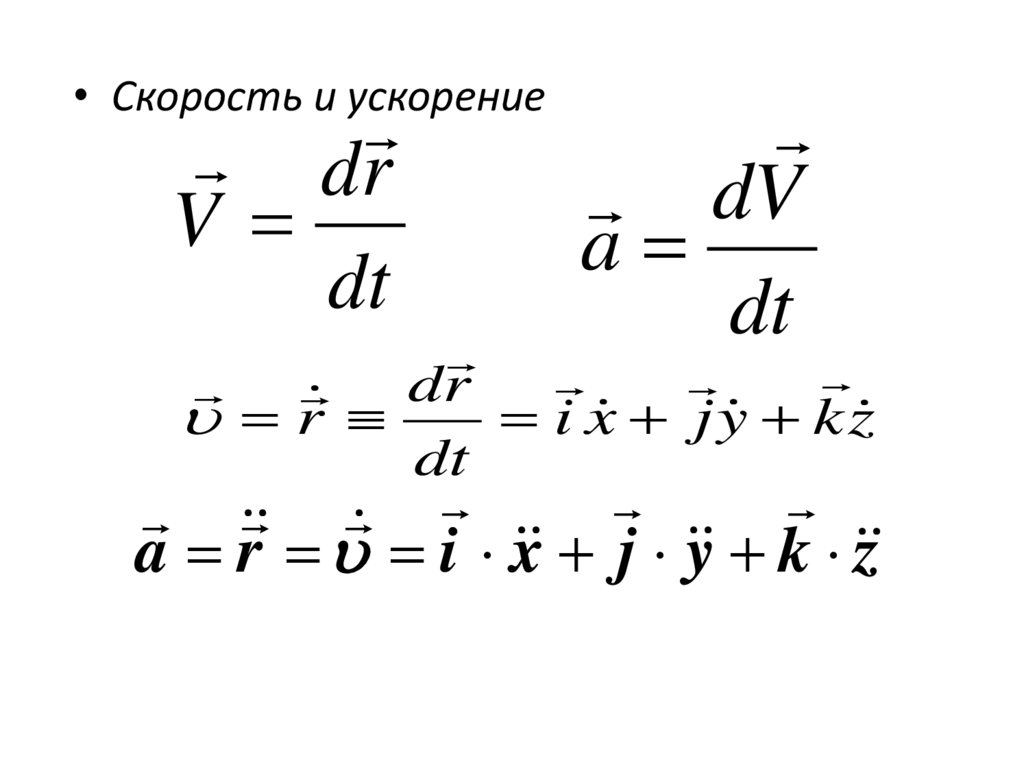
















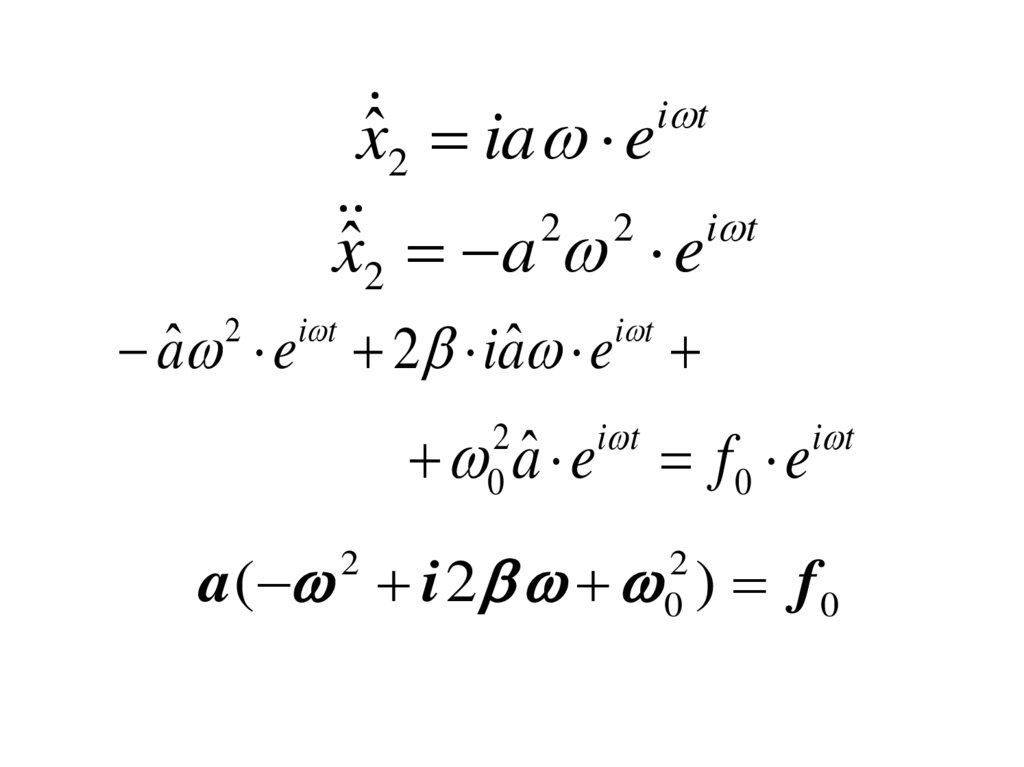
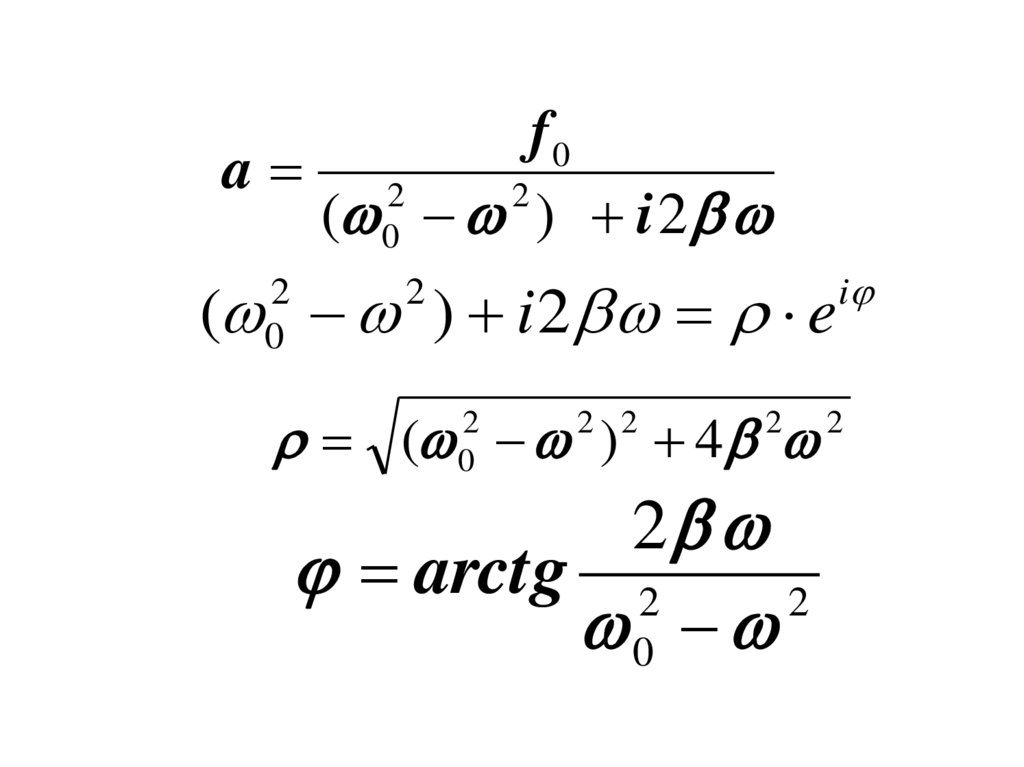

















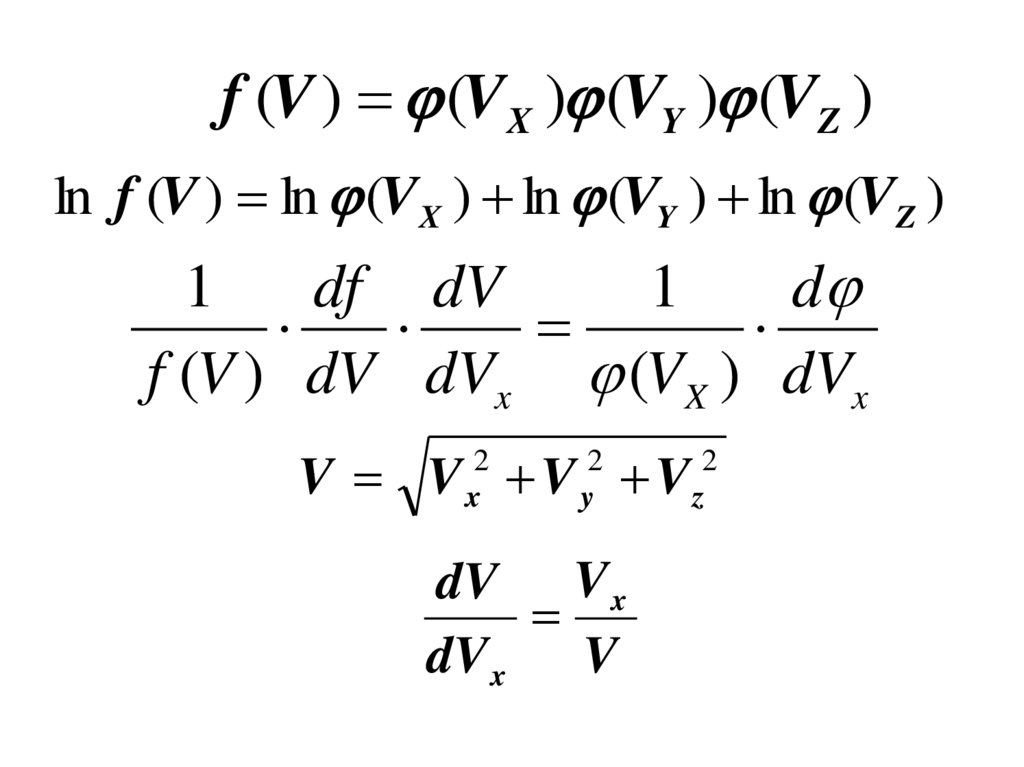
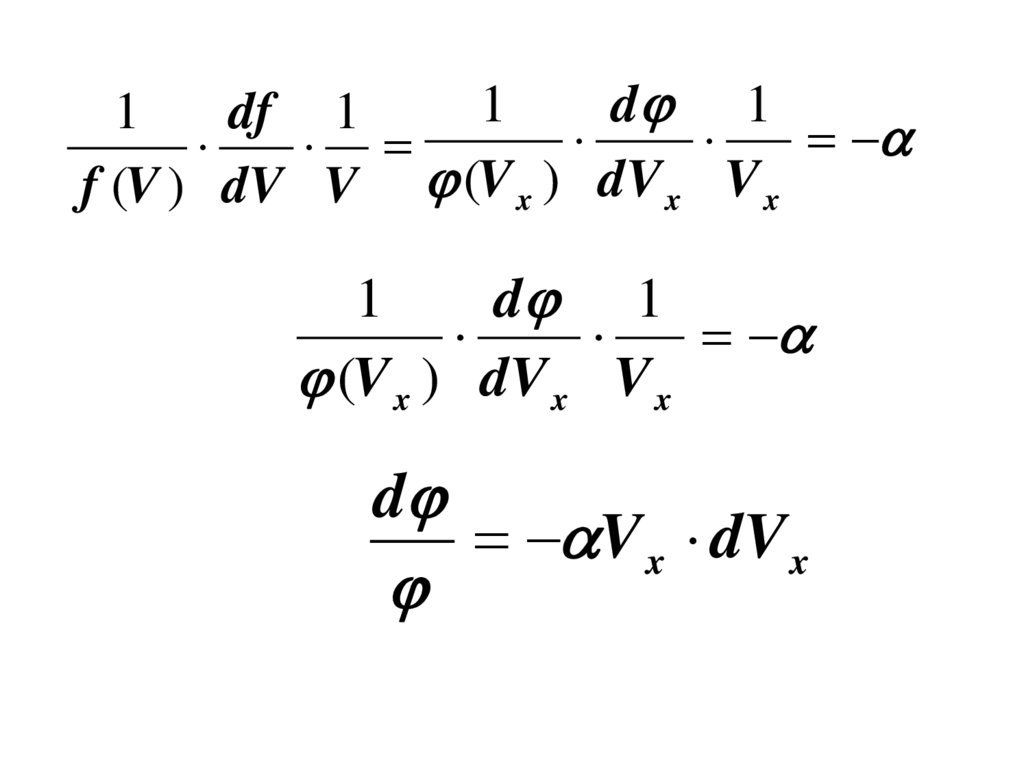

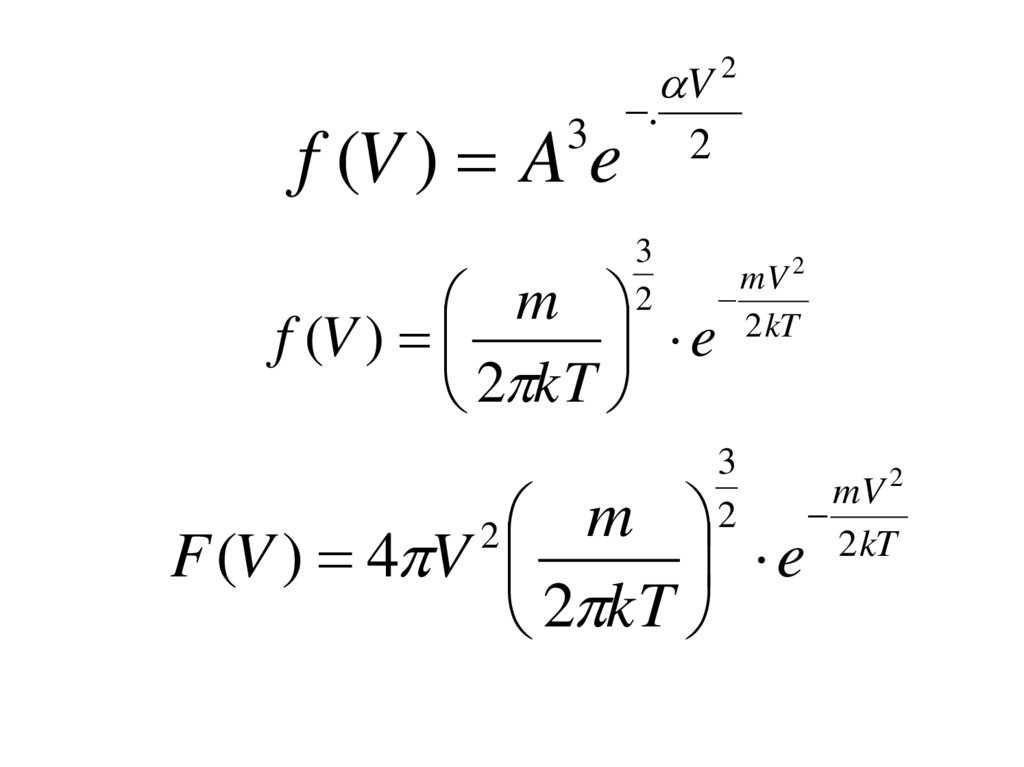


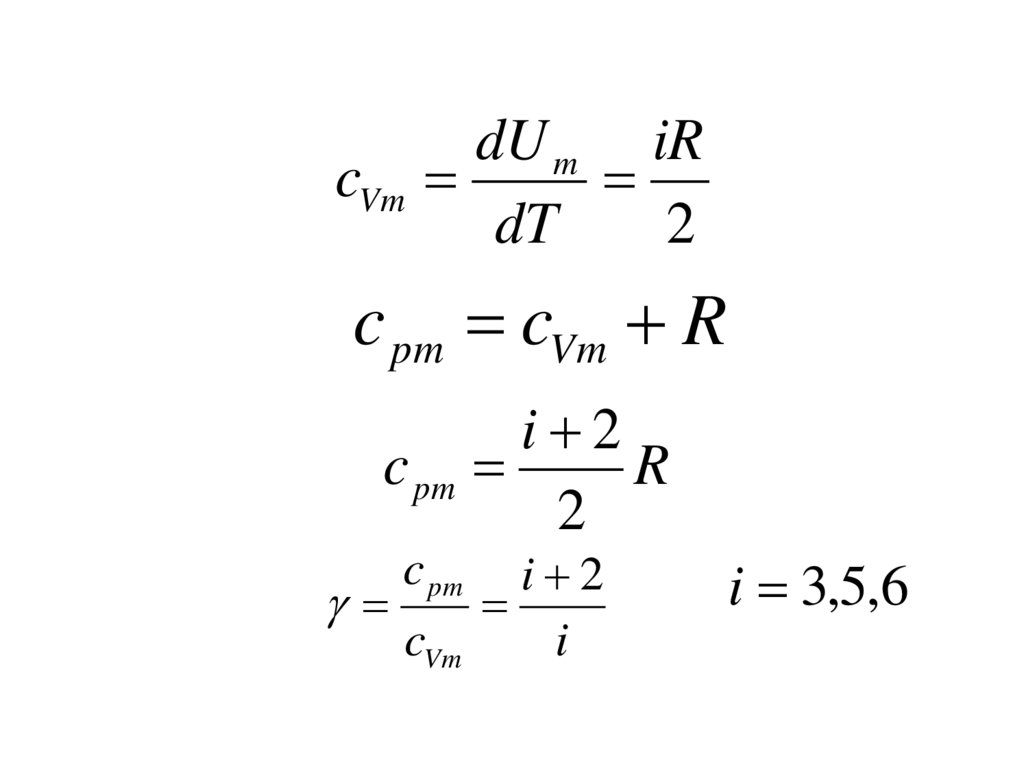




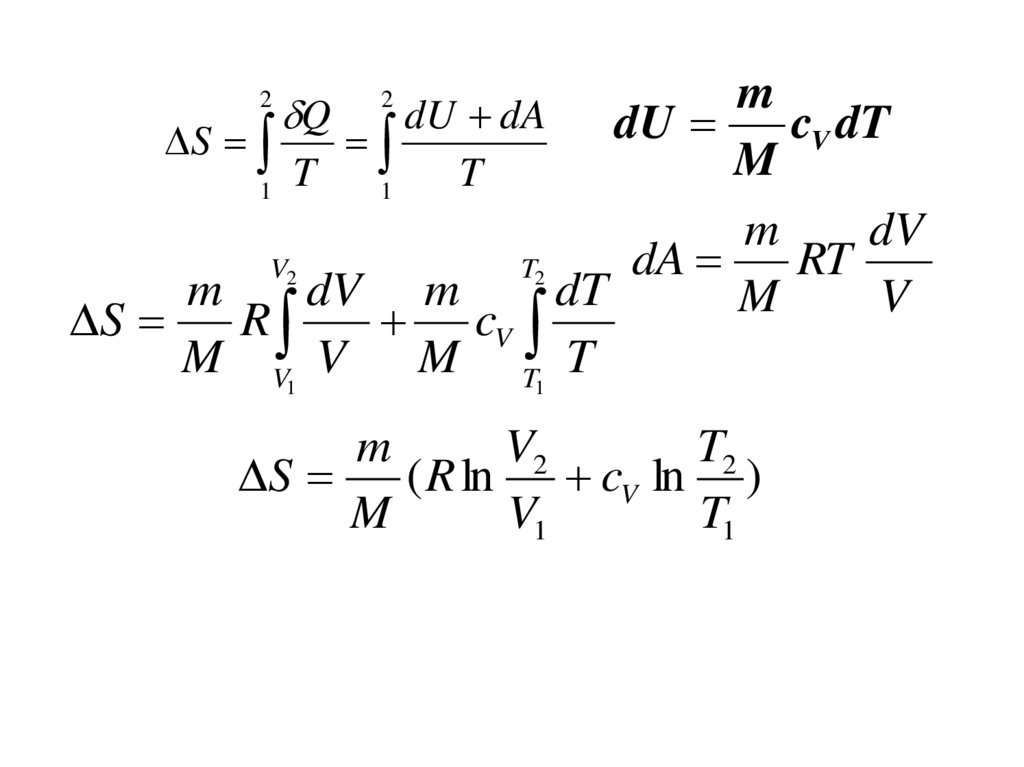









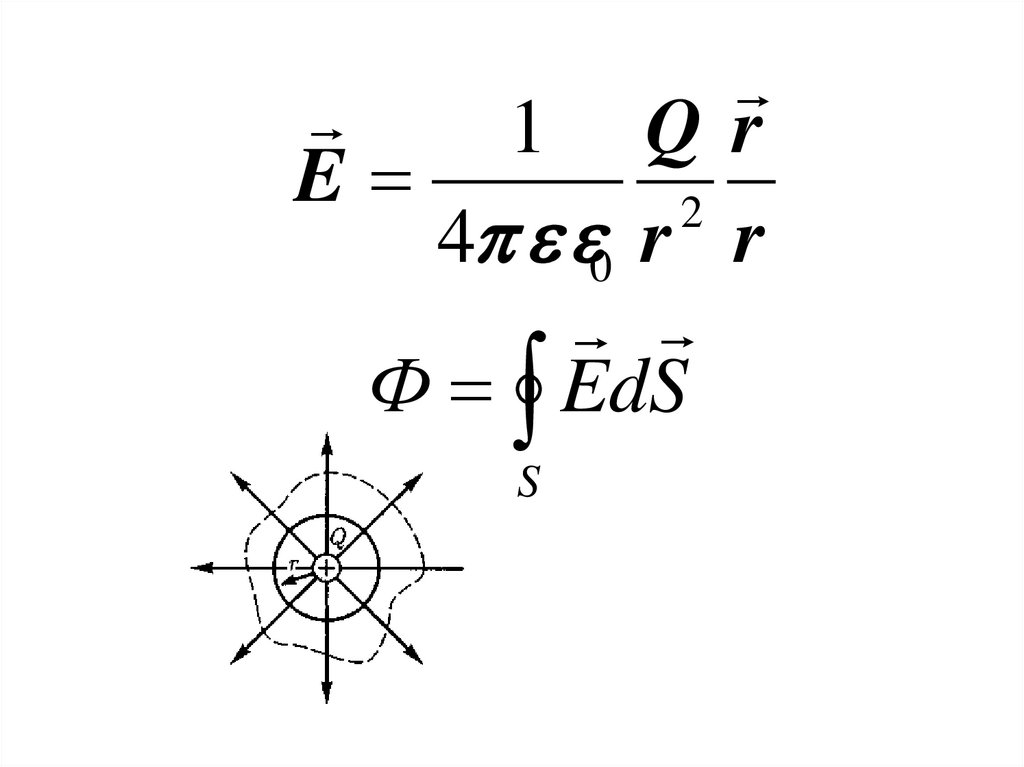
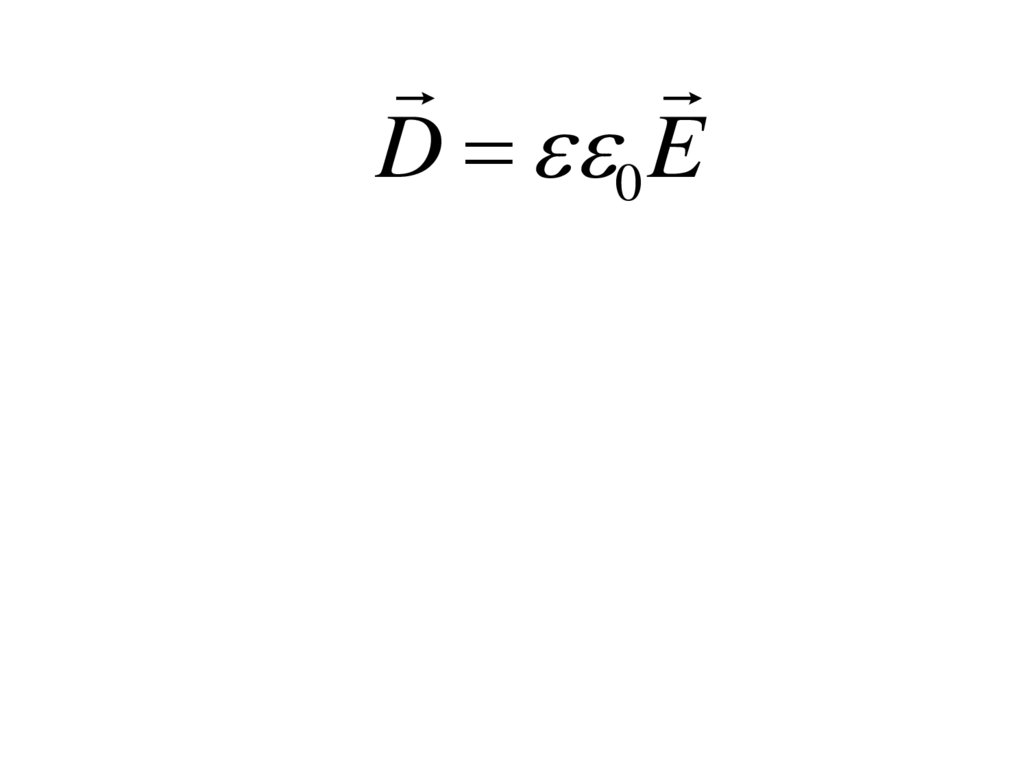

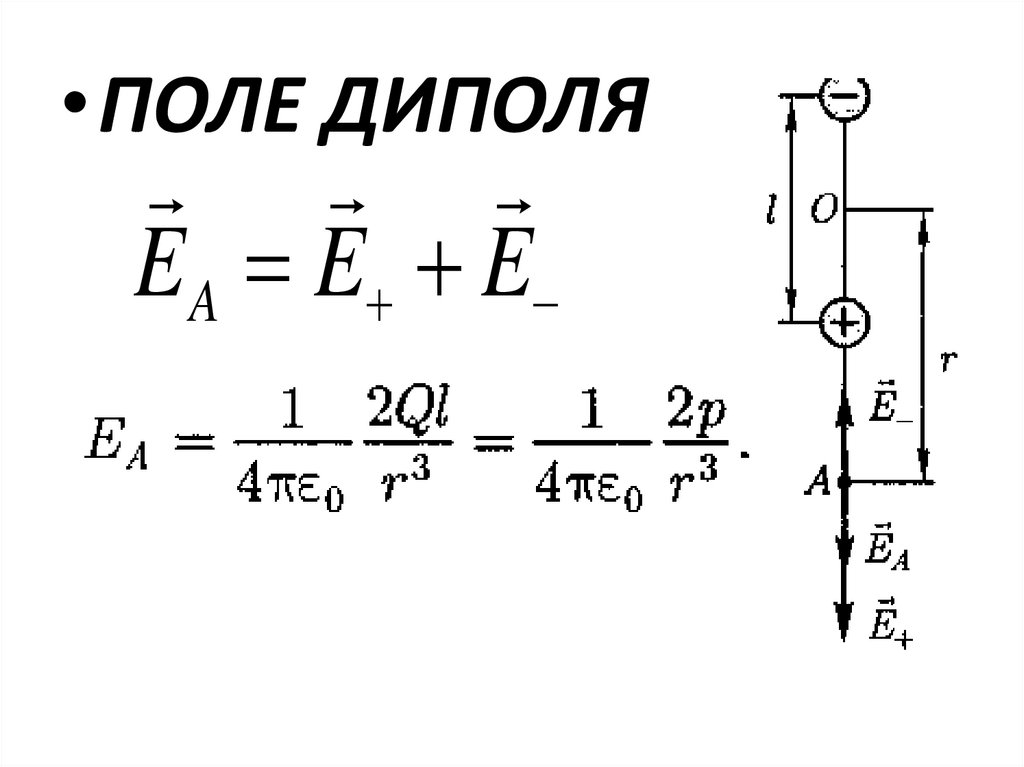





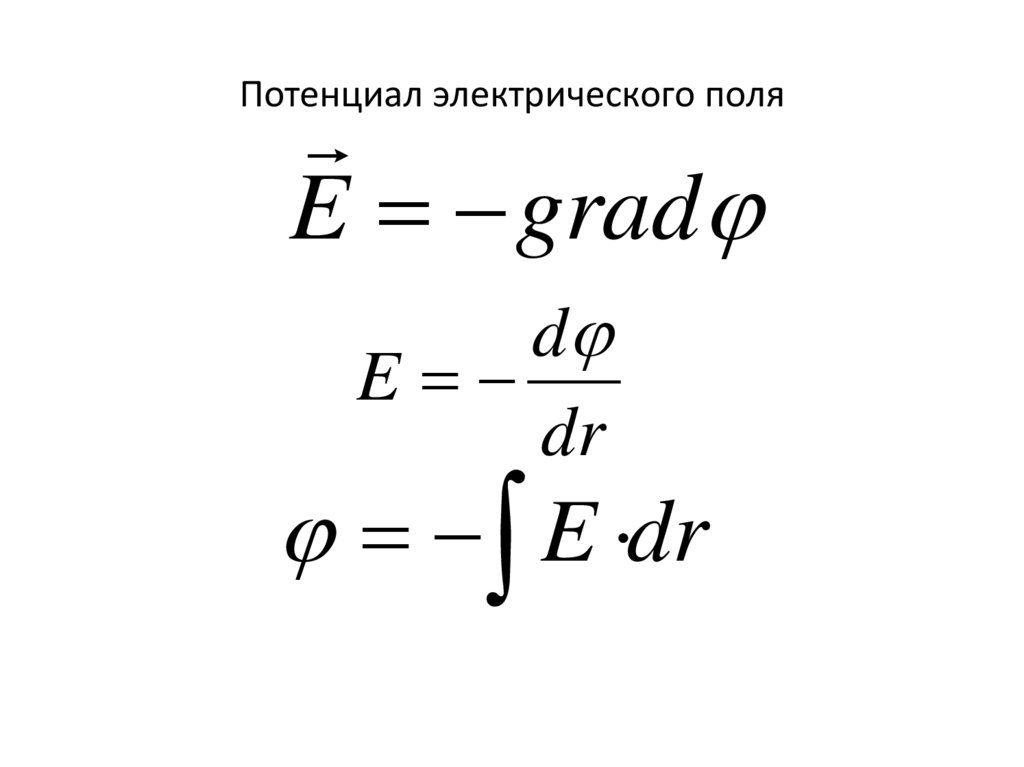





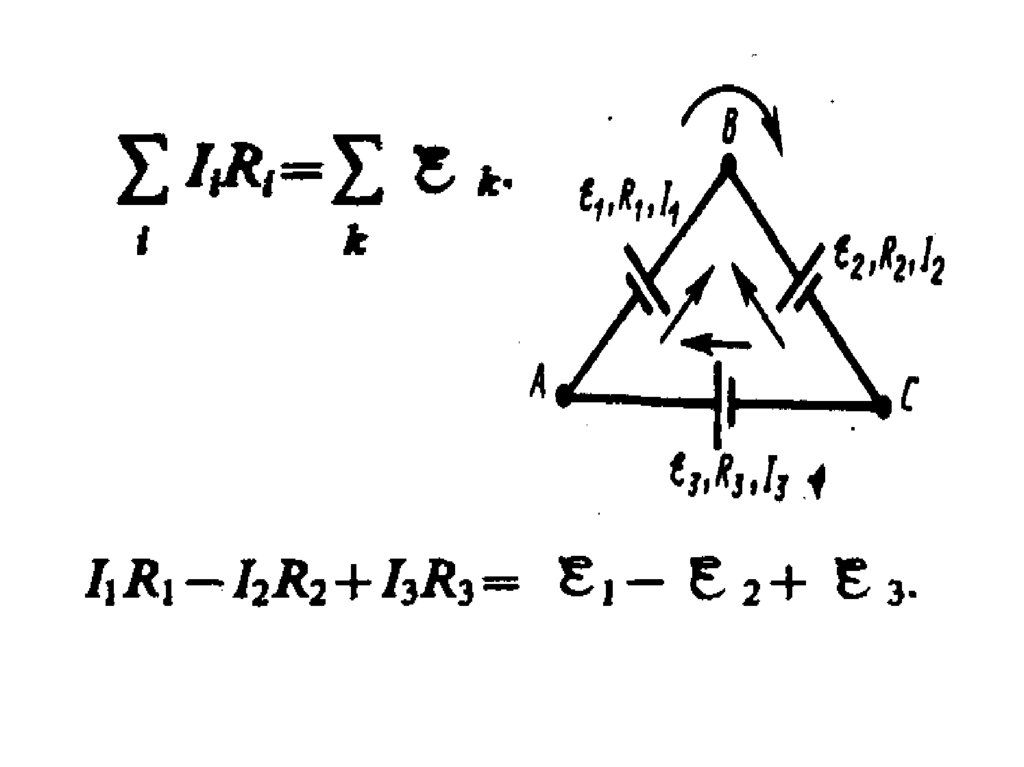




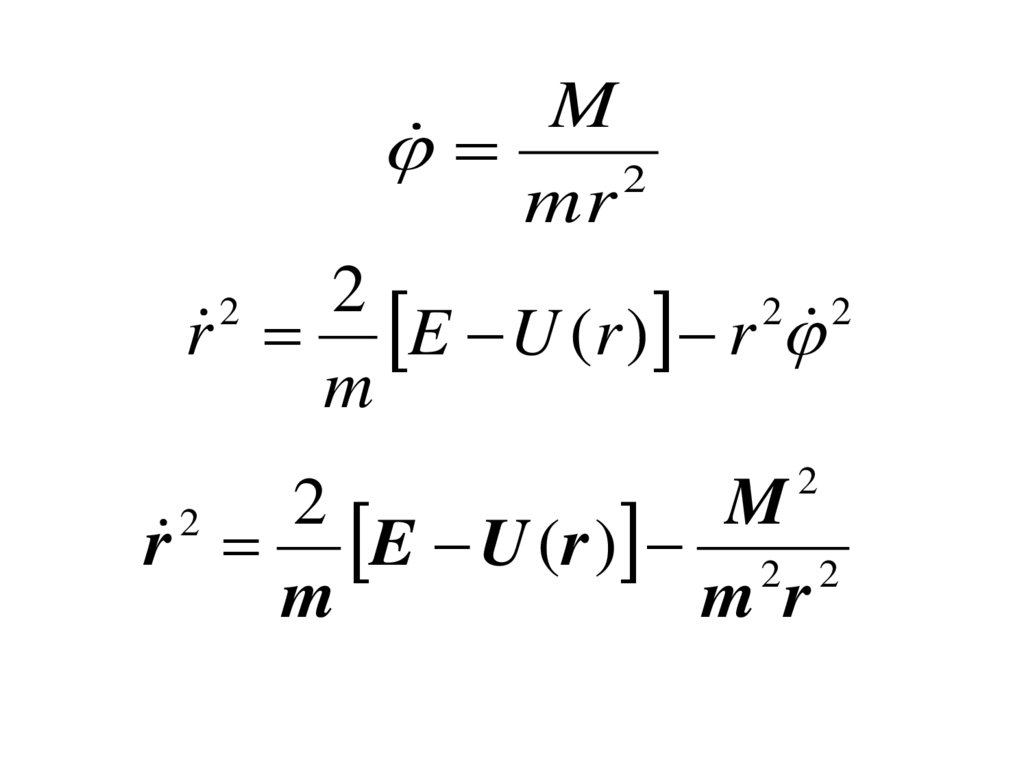
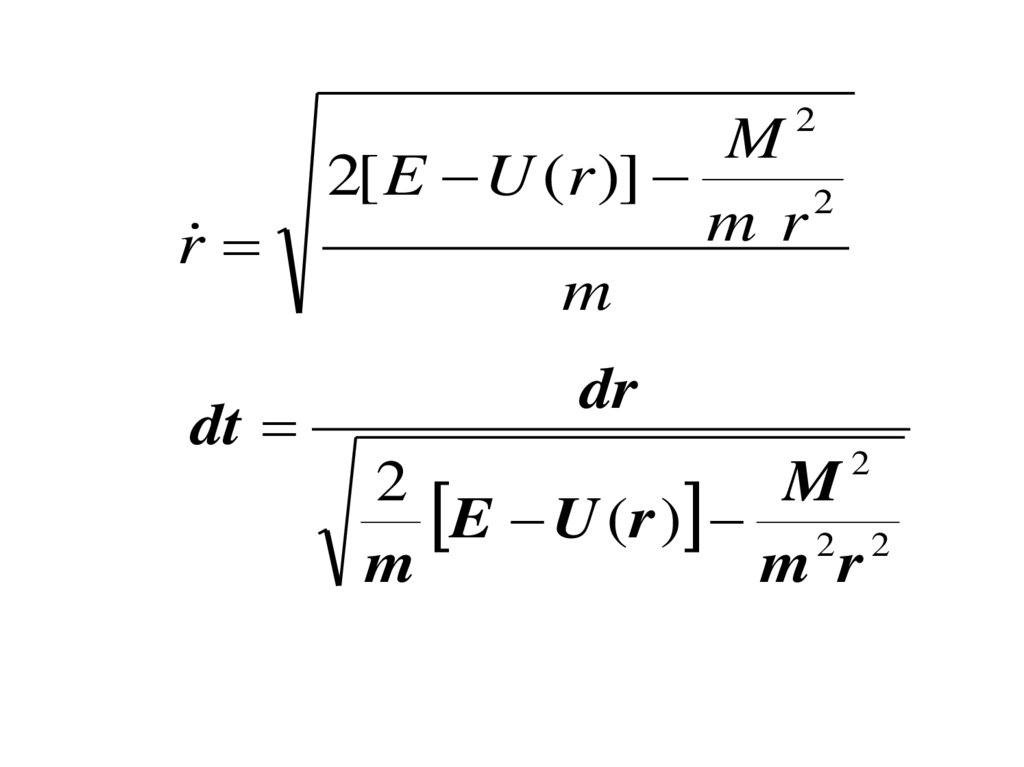
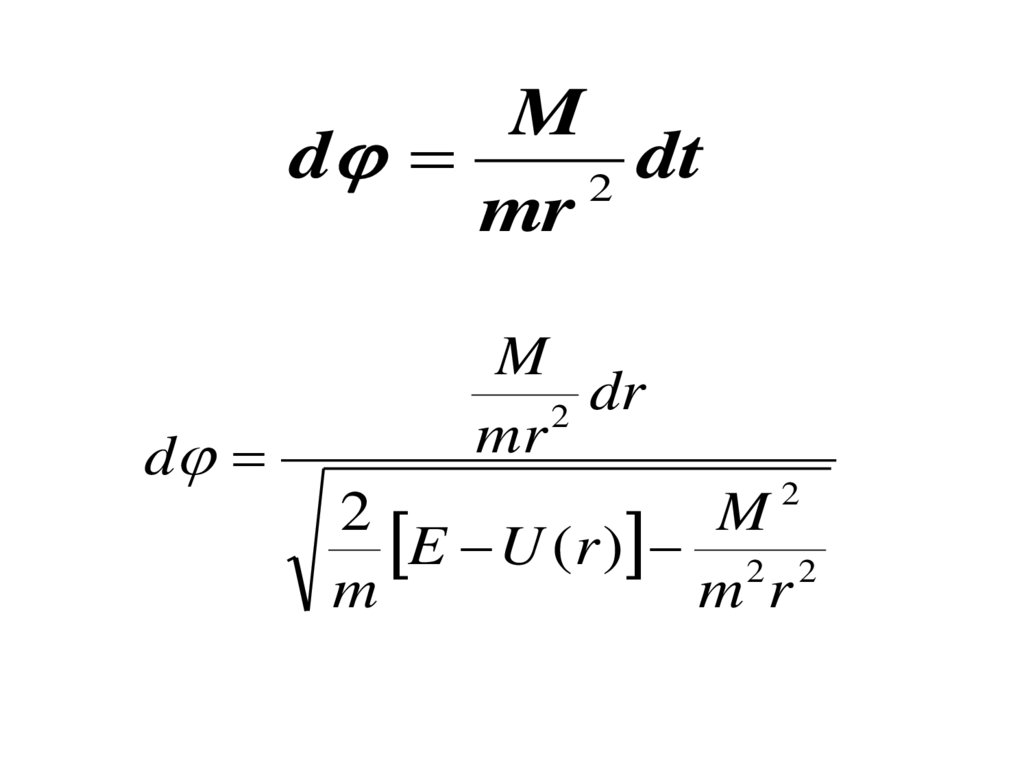
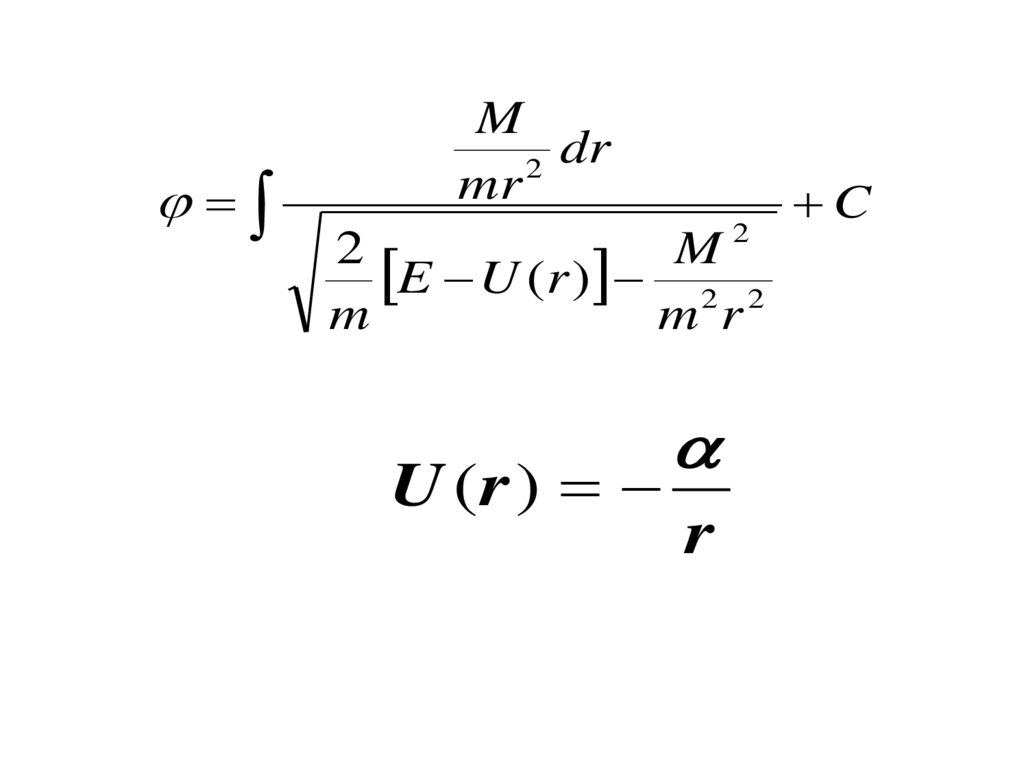
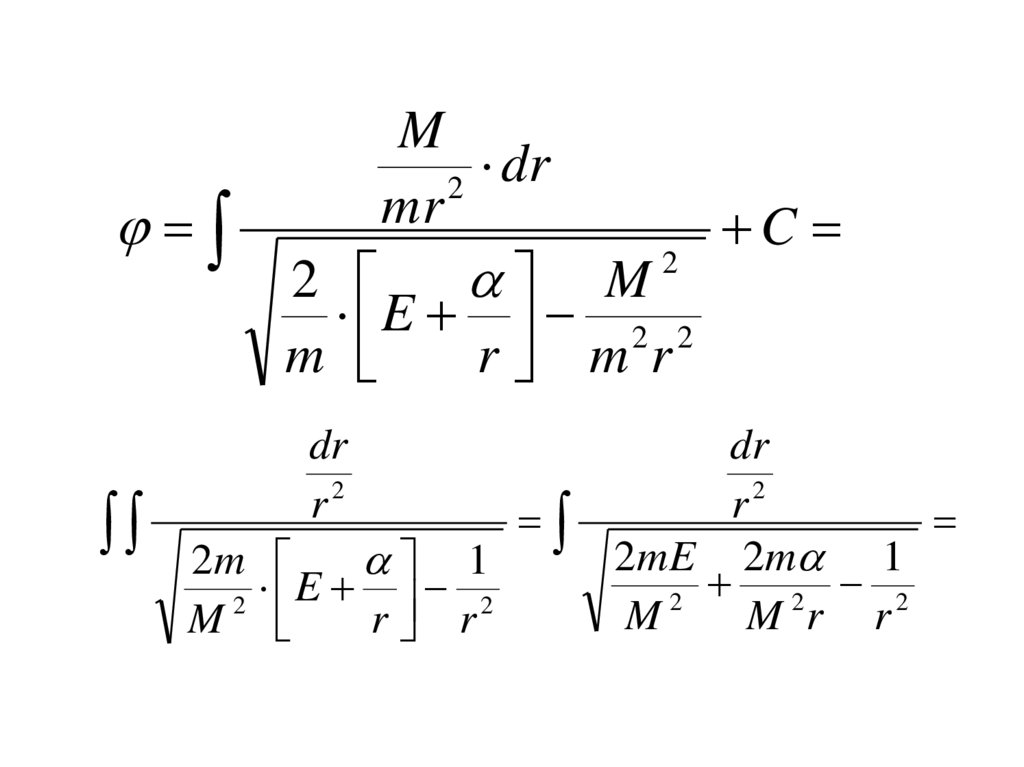
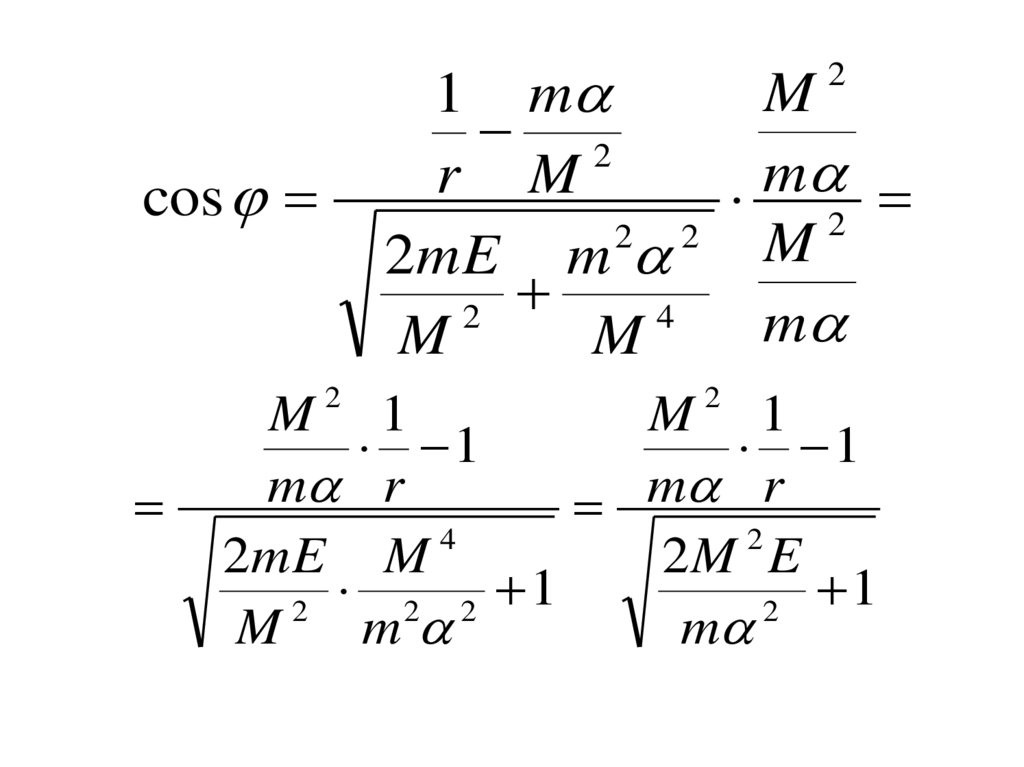

 Физика
Физика








