Пряма в просторі. Площина

1. Кафедра вищої математики ім. проф. Можара В.І.

ПРЯМА В ПРОСТОРІ. ПЛОЩИНА

2. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА

План
1. Різні рівняння площини
2. Кут між двома площинами
3. Відстань від точки до площини
4. Різні рівняння прямої лінії в просторі
5. Кут між двома прямими в просторі
6. Кут між прямою і площиною
7. Приклади розв’язання типових завдань
8. Запитання для самоконтролю

3. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 1. Різні рівняння площини

Загальне рівняння площини
Нехай площина проходить через точку
M 0 x0 , y 0 , z 0
перпендикулярно вектору N A, B, C .
Цими умовами визначається єдина площина в просторі Оxyz.
Візьмемо в площині довільну точку
M x, y, z .
Тоді
вектор
буде
M 0 M x x0 , y y 0 , z z 0
перпендикулярним вектору N A; B; C .
Значить, скалярний добуток цих векторів дорівнює нулеві,
тобто N M 0 M 0.

4. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 1. Різні рівняння площини

Загальне рівняння площини
Одержане рівняння запишемо в координатній формі:
A x x0 B y y 0 C z z 0 0
– рівняння площини, перпендикулярної заданому вектору
нормалі N A; B; C і проходить через задану точку
M 0 x0 , y 0 , z 0 .
Рівняння площини, записане у вигляді
Ax By Cz D 0,
де D Ax0 By0 Cz0 ,
називається загальним рівнянням площини.

5. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 1. Різні рівняння площини

Частинні випадки загального рівняння площини
Ax By Cz D 0 :
1. Якщо D 0 , то загальне рівняння набуває вигляду
Ax By Cz 0 . Цьому рівнянню задовольняє точка
.
O 0, 0, 0 . Тобто, рівняння визначає площину, яка
проходить через початок координат.
2. Якщо C 0 , то маємо рівняння Ax By D 0 . Цьому
рівнянню
відповідає
вектор
який
N A, B, 0 ,
перпендикулярний до вісі Оz. Тобто, площина паралельна
вісі Оz; якщо B 0 – паралельна вісі Оу; якщо A 0 –
паралельна вісі Ох.

6. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 1. Різні рівняння площини

Частинні випадки загального рівняння площини
Ax By Cz D 0 :
3. Якщо дорівнюють нулеві коефіцієнти при двох із
координатних змінних, то площина паралельна відповідній
координатній площині.
4. Якщо дорівнює нулеві коефіцієнт при одній із
координатних змінних і D=0, то площина проходить через
відповідну координатну вісь.
5. Якщо дорівнюють нулеві коефіцієнти при двох
координатних змінних і D=0, то площина співпадає з
відповідною координатною площиною. Так, наприклад,
площина задана рівнянням 5z=0. Маємо рівняння
координатної площини Oxy.

7. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 1. Різні рівняння площини

Рівняння площини, яка проходить через три задані точки
Нехай задано три точки
M 1 x1 , y1 , z1 , M 2 x 2 , y 2 , z 2 і M 3 x3 , y3 , z 3 , які не лежать на одній
прямій.
Візьмемо на площині довільну точку M x, y, z , яка
лежить в одній площині точками M 1 , M 2 , M 3 , і утворимо
вектори
M1M x x1, y y1, z z1 , M 2M x x2 , y y2 , z z2 ,
M 3M x x3 , y y3 , z z3 .

8. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 1. Різні рівняння площини

Рівняння площини, яка проходить через три задані точки
Ці три вектори лежать в одній площині, значить вони
компланарні і їх мішаний добуток дорівнює нулю, тобто
x x1 y y1 z z1
M 1M M 2 M M 3M 0 або x x 2 y y 2 z z 2 0
x x3 y y 3 z z 3
– рівняння площини яка проходить через три задані точки.

9. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 1. Різні рівняння площини

Рівняння площини у відрізках на осях
Нехай площина відтинає на осях координат Ох, Оу, Оz
відповідно відрізки а, в, с, тобто проходить через точки
A a, 0, 0 , B 0, b, 0 , C 0, 0, с .
Підставимо координати цих точок в рівняння площини, яка
проходить через три задані точки , отримаємо
x a y z
a
b 0 0.
a
0 c

10. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 1. Різні рівняння площини

Рівняння площини у відрізках на осях
Розкривши визначник, отримаємо
bcx abc abz acy 0,
bcx abz acy abc
або
x y z
1
a b c
– рівняння площини у відрізках на осях.

11. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 2. Кут між двома площинами

Нехай
A1 x B1 y C1 z D1 0 – рівняння площини 1 ;
A2 x B2 y C2 z D2 0 – рівняння площини .
2
Нормальним вектором площини 1 буде вектор N A1, B1, C1 ,
а 2 – вектор N A2 , B2 , C2 .
Косинус кута між цими векторами, а значить і між
площинами, обчислюється за відомою формулою (скалярний
добуток):

12. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 2. Кут між двома площинами

cos
A1 A2 B1B2 C1C2
A12
B12
C12
A22
B22
C22
.
Умова перпендикулярності двох площин співпадає з
умовою перпендикулярності векторів N1 і N 2 , і має вигляд:
A1 A2 B1B2 C1C2 0.
Умова паралельності двох площин співпадає з умовою
колініарності векторів ( N1 N 2 ):
A1
B
C
1 1.
A2
B2
C2

13. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 3. Відстань від точки до площини

Аналогічно з формулою знаходження відстані від точки
до прямої на площині можна записати формулу
знаходження відстані від точки
M x0 , y 0 , z 0
до площини
Ax By Cz D 0.
Вона має вигляд:
d
Ax0 By0 Cz0 D
A B C
2
2
2
.

14. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 4. Різні рівняння прямої лінії в просторі

Канонічне рівняння прямої в просторі
Пряму L в просторі можна визначити точкою
M 1 x1 ; y1 ; z1 , яка належить цій прямій, і направляючим
вектором q l , m, n цієї прямої ( q L ).
Побудуємо вектор
M1M x x1, y y1, z z1 ,
M x; y; z L .

15. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 4. Різні рівняння прямої лінії в просторі

Канонічне рівняння прямої в просторі
Вектори M 1M і q - колінеарні, а тому їх відповідні
координати пропорційні:
x x1 y y1 z z1
.
l
m
n
Рівняння називають канонічним рівнянням прямої в
просторі.

16. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 4. Різні рівняння прямої лінії в просторі

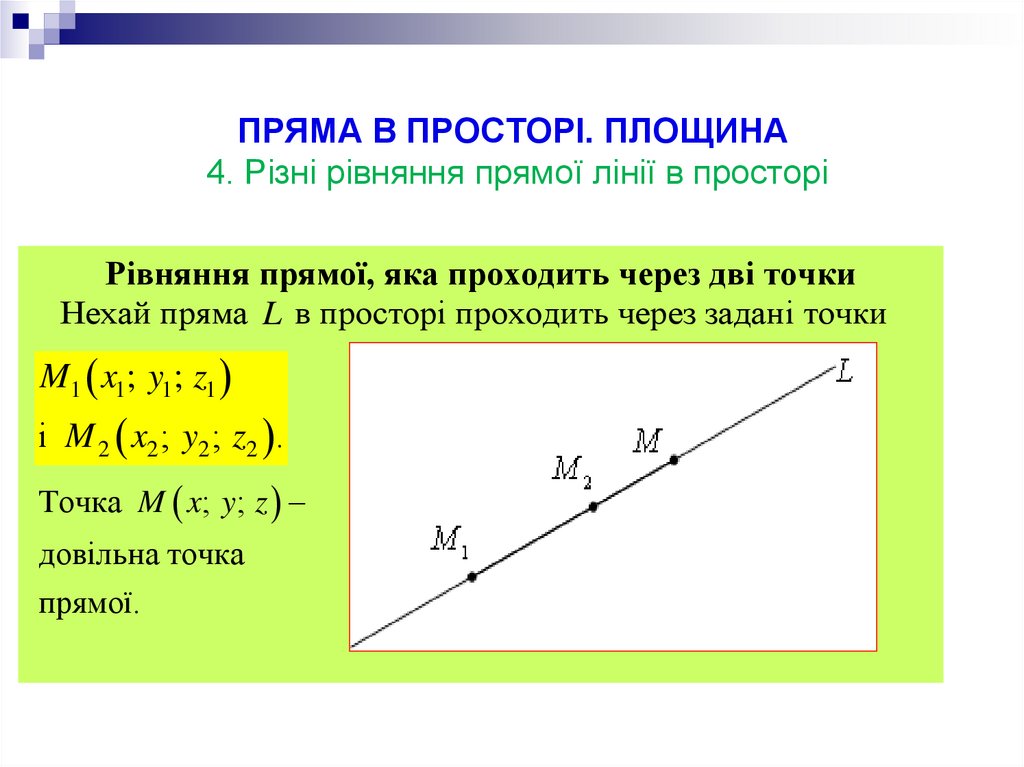
Рівняння прямої, яка проходить через дві точки
Нехай пряма L в просторі проходить через задані точки
M1 x1; y1; z1
і M 2 x2 ; y2 ; z2 .
Точка M x; y; z
довільна точка
прямої.

17. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 4. Різні рівняння прямої лінії в просторі

Рівняння прямої, яка проходить через дві точки
Побудуємо вектори M M x x , y y , z z ,
1
M1M 2 x2 x1, y2 y1, z2 z1 ,
1
1
1
M x; y; z L .
Вектори M 1M і M 1 M 2 – колінеарні, а тому їх відповідні
координати пропорційні:
x x1
y y1
z z1
x 2 x1 y 2 y1 z 2 z1
– рівнянням прямої, яка проходить через дві задані
точки.

18. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 4. Різні рівняння прямої лінії в просторі

Параметричне рівняння прямої
Позначимо значення відношень параметром t R :
x x1
t,
l
x x1 y y1 z z1
y y1
t,
t,
l
m
n
m
z z1
t,
n
x x1 lt ,
y y1 mt ,
z z nt .
1
Останню систему називають параметричним рівнянням
прямої.

19. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 4. Різні рівняння прямої лінії в просторі

Рівняння прямої, як лінія перетину двох площин
Розглянемо систему рівнянь
A1x B1 y C1z D1 0 1 ,
(1)
A2 x B2 y C2 z D2 0 2 .
Кожне з цих рівнянь визначає площину, а лінією їх
перетину є пряма L.
Рівняння (1) називають загальними рівняннями прямої.
Від рівнянь (1) можна перейти до канонічного рівняння
прямої.

20. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 4. Різні рівняння прямої лінії в просторі

Рівняння прямої, як лінія перетину двох площин
Для цього необхідно знати координати направляючого
вектора
q l; m; n , координати точки M1 x1; y1; z1 L.
Точку M 1 беруть, як перетин даної прямої із однією із
координатних площин:
якщо з площиною Оху, то в системі (1) покладають z 0;
якщо з площиною Охz, то
якщо з площиною Oyz, то
у 0;
x 0.

21. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 4. Різні рівняння прямої лінії в просторі

Рівняння прямої, як лінія перетину двох площин
i
j
k
q N1 N 2 A1 B1 C1
A2 B2 C2
де N1 A1, B1, C1 і N 2 A2 , B2 , C2 нормальні вектори
площин 1 і 2 .

22. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 5. Кут між двома прямими в просторі

Нехай прямі L1 і L 2 задані канонічними рівняннями:
x x1 y y1 z z1 x x2
y y2
z z2
,
.
l1
m1
n1
l2
m2
n2
Під кутом між цими прямими розуміють кут між
направляючими векторами q1 l1, m1, n1 і q2 l2 , m2 , n2
цих прямих.
l1l2 m1m2 n1n2
cos
.
l12 m12 n12 l22 m22 n22

23. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 5. Кут між двома прямими в просторі

Якщо L1 L2 , то cos 0 l1l2 m1m2 n1n2 0;
якщо L1 L2 , то координати цих векторів пропорційні:
паралельні і їхні направляючі вектори, тобто
l1 m1 n1
.
l2 m2 n2

24. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 6. Кут між прямою і площиною

Нехай пряму задано канонічним рівнянням
x x1 y y1 z z1
,
l
m
n
площину – рівнянням загального виду Ax By Cz D 0.
Кутом між прямою і площиною називається любий із
двох суміжних кутів, які утворені прямою і її проекцією на
цю площину, який обчислюється за формулою
sin
Al Bm Cn
A2 B 2 C 2 l 2 m2 n 2
.

25. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 7. Приклади розв’язання типових завдань

Приклад. Знайти рівняння площини, яка проходить через
три точки M1 (1; 2; 1), M 2 ( 1; 0; 4), M 3 ( 2; 1; 1).
Розв’язання.
x 1 y 2 z 1
2
2
11 x 1 11 y 2 0 z 1 0
5 0
3
3
2
x y 1 0.
Це рівняння визначає площину, яка паралельна вісі Oz.

26. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 7. Приклади розв’язання типових завдань

Приклад. Обчислити косинус кута між двома площинами
3x y 2 z 4 0 ,
x 4y z 5 0 .
Розв’язання.
По формулі cos
A1 A2 B1B2 C1C2
A12
B12
C12
A22
B22
C22
,
якщо врахувати, що A1 3; B1 1; C1 2 , A2 1; B2 4; C 2 1 ,
одержимо:
3 4 2
5
cos
.
14 18 6 7

27. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 7. Приклади розв’язання типових завдань

Приклад. Обчислити відстань від точки A 2; 3; 1 до
площини 7 x 6 y 6 z 42 0 .
Розв’язання.
Відстань від точки до площини обчислюємо за формулою
d
Ax0 By0 Cz0 D
A B C
2
2
2
.
в якій A 7; B 6; C 6; D 42, x0 2, y0 3, z0 1.
Підставляючи ці значення у формулу одержимо
d 4.

28. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 7. Приклади розв’язання типових завдань

x y z 1 0,
Приклад. Привести рівняння прямої
до
2 x y 3 z 5 0
канонічного вигляду.
Розв’язання.
Направляючий вектор цієї прямої обчислимо за формулою
i
j
k
i
j
k
q N1 N 2 A1 B1 C1 1 1 1 4 i j 3k.
A2 B2 C2
2 1 3

29. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 7. Приклади розв’язання типових завдань

Покладемо z=0 і знайдемо розв’язок системи
x y 1 0,
2 x y 5 0.
Розв’язавши систему, маємо x 2, y 1.
Отже, точка M 1 буде мати координати: M 1 2; 1; 0
і канонічне рівняння прямої запишеться у вигляді:
x 2 y 1 z
.
4
1
3

30. ПРЯМА В ПРОСТОРІ. ПЛОЩИНА 8. Запитання для самоконтролю

1.Записати загальне рівняння площини і дати геометричне
пояснення коефіцієнтів при змінних в цьому рівнянні.
2. Записати рівняння площини у відрізках і дати геометричне
пояснення коефіцієнтів в цьому рівнянні.
3. Записати рівняння площини, що проходить через три дані
точки.
4. Записати нормальне рівняння площини і дати геометричне
пояснення коефіцієнтів при змінних і вільному члену в
цьому рівнянні.
5. Що називається відстанню від точки до площини і за яким
правилом вона обчислюється?