Доверительные интервалы. Расчет репрезентативного объема выборки. Лекция 8

1. ЛЕКЦИЯ 8

ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ.
РАСЧЕТ РЕПРЕЗЕНТАТИВНОГО
ОБЪЕМА ВЫБОРКИ

2. Суть «доверительного интервала» (confidence interval)

Не зная точно, чему равна
некоторая величина, мы с
заданной вероятностью можем
указать диапазон значений,
в котором она находится.

3. 8.1. Доверительный интервал для разности средних и долей

4. Поправка, благодаря которой распределение t всегда будет симметрично относительно 0

( x1 x2 ) ( 1 2 )
t
s x1 x2

5. Свойства t-распределения :

100α % всех возможных
значений t расположены
левее -tα или правее +tα ;
Остальные 100(1 – α) %
значений t попадают в
интервал от -tα до +tα

6. …т.е. в 100(1 – α) % всех случаев мы имеем:

( x1 x2 ) ( 1 2 )
t
t
sx1 x2

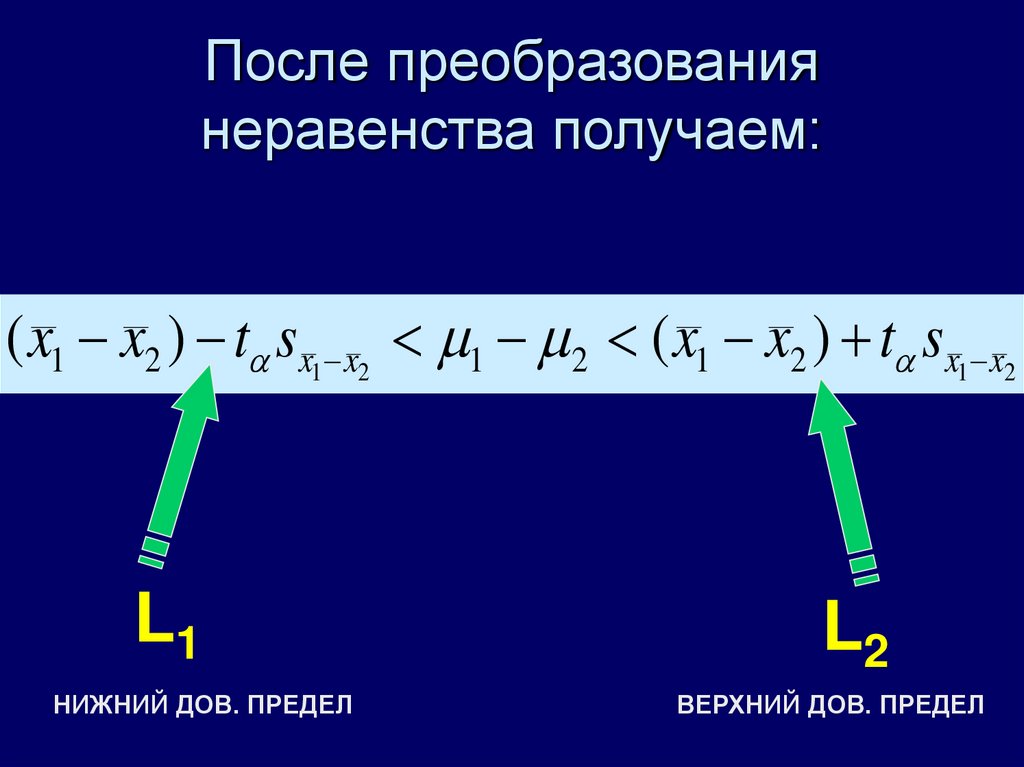
7. После преобразования неравенства получаем:

( x1 x2 ) t sx1 x2 1 2 ( x1 x2 ) t sx1 x2
L1
НИЖНИЙ ДОВ. ПРЕДЕЛ
L2
ВЕРХНИЙ ДОВ. ПРЕДЕЛ

8. 100(1 – α)-процентный интервал для разности истинных долей:

( pˆ1 pˆ 2 ) z s pˆ1 pˆ 2 p1 p2 ( pˆ1 pˆ 2 ) z s pˆ1 pˆ 2

9. 8.2. Доверительный интервал для средней арифметической и доли

10. 100(1 – α)-процентный доверительный интервал для средней арифметической:

x t sx x t sx

11. 100(1 – α)-процентный доверительный интервал для доли:

pˆ t s pˆ p pˆ t s pˆ

12. Следует помнить!!!

При снижении уровня значимости
(например, с 0.05 до 0.01)
доверительный интервал
расширяется, т.к.
увеличивается
соответствующее
критическое значение t.

13. 8.3. Проверка гипотез с помощью доверительных интервалов

14. Правило:

Если 100(1 – α)-процентный
интервал разности средних не
содержит 0, то различия
статистически значимы (P < α);
напротив, если этот интервал
содержит 0, то различия
статистически не значимы (P > α).

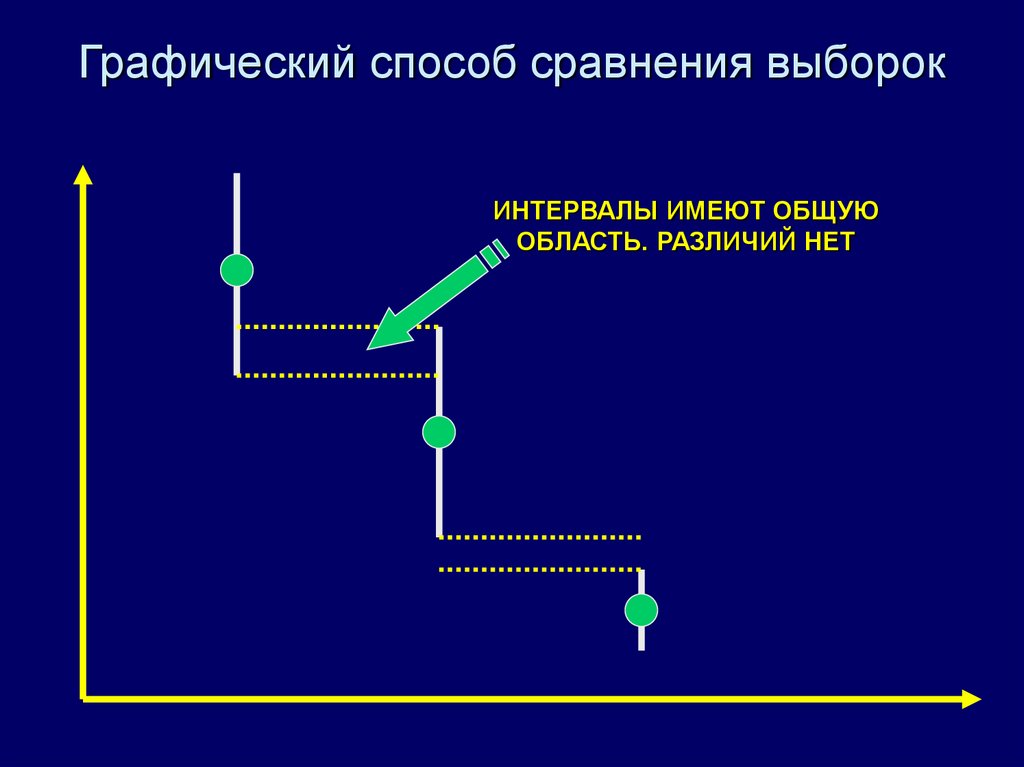
15. Графический способ сравнения выборок

ИНТЕРВАЛЫ ИМЕЮТ ОБЩУЮ
ОБЛАСТЬ. РАЗЛИЧИЙ НЕТ

16. 8.4. Расчет репрезентативного объема выборки

17. Как определить «оптимальный» объем выборки???

2 2
n
t s
2
, где
tsx

18. Правило:

Чтобы уменьшить ошибку
выборочной средней в К
раз, объем выборки нужно
увеличить в К2 раз.