Статистическое оценивание. Выборочный метод. Требования, предъявляемые к выборке. (Лекция 4)

1. Тема: «Статистическое оценивание»  

Лекция 6.
ТЕМА: «СТАТИСТИЧЕСКОЕ
ОЦЕНИВАНИЕ»

2. План лекции:

Выборочный метод.
Требования,
предъявляемые к
выборке. Рандомизация.
Способы отбора вариант
в выборку.
Понятие статистической
оценки. Точечные и
интервальные оценки.
Несмещенность,
состоятельность и
эффективность оценок.
Понятие доверительного
интервала. Оценки и их
доверительные
интервалы для
математического
ожидания и дисперсии
нормального
распределения.
Доверительные
вероятности. Примеры
получения оценок для
почвенных данных.

3.

Выборочный метод. Требования,
предъявляемые к выборке.
Рандомизация. Способы отбора вариант
в выборку.

4.

Совокупность из которой отбирается некоторая
часть ее членов для совместного изучения
называется генеральной.
N – объем генеральной совокупности:
N →∞

5.

Часть генеральной совокупности отобранная тем
или иным способом называется выборочной
совокупностью (или выборкой).
n – объем выборки:
n≥2

6.

Выборочный метод является
основным
при
изучении
статистических совокупностей.
Преимущества:
- сокращает время и затраты труда,
- позволяет получать информацию о таких совокупностях сплошное
обследование которых практически невозможно или не
целесообразно.

7.

Выборка должна быть представительной –
репрезентативной (от лат. represento –
представляю), т.е. возможно полнее
отображать
структуру
генеральной
совокупности.

8.

Рендомизация (от англ. random - случай) –
случайный отбор вариант из генеральной
совокупности, что обеспечивает равную
возможность для всех членов генеральной
совокупности попасть в состав выборки.

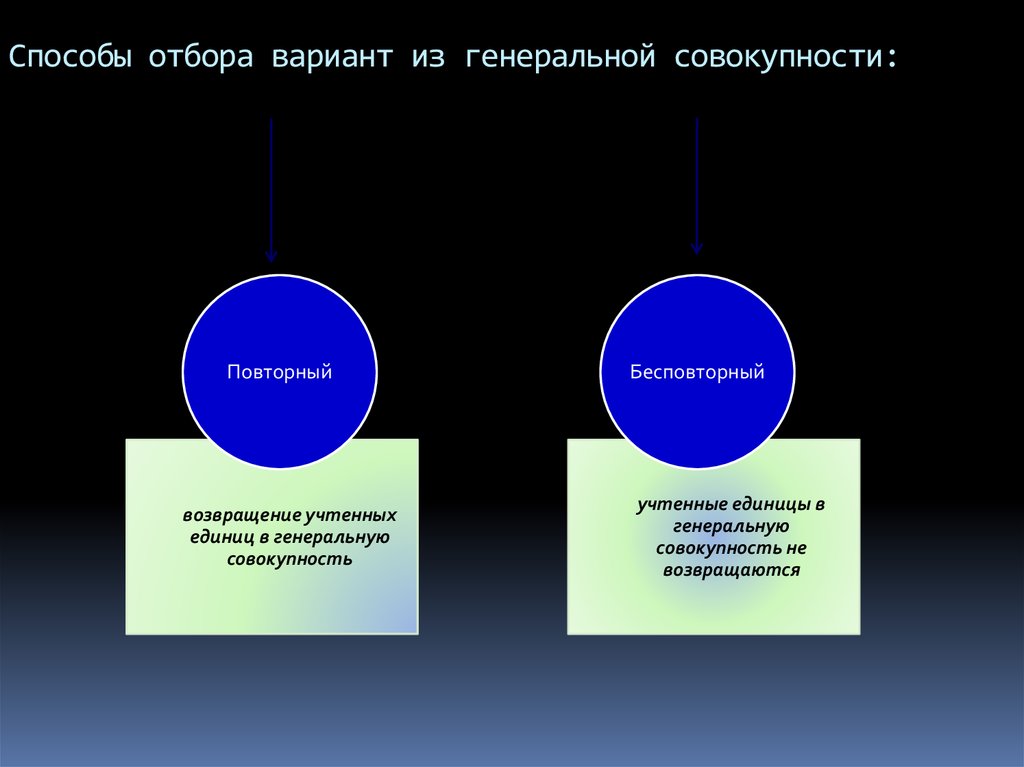
9. Способы отбора вариант из генеральной совокупности:

Повторный
возвращение учтенных
единиц в генеральную
совокупность
Бесповторный
учтенные единицы в
генеральную
совокупность не
возвращаются

10. Виды отбора единиц из генеральной совокупности:

Типический (или групповой);
Серийный (или гнездовой);
Механический.

11.

Механический отбор (систематический) когда образцы для анализа отбирают
через равные интервалы расстояния
(времени).

12. Таблица случайных чисел

13. Послойная выборка

Рандомизацию
проводят
дифференцированно для каждой части
(зоны, слоя и т.п.) причем объемы
подвыборок
в
этих
частях
пропорциональны доле их участия в
составе целого объекта.

14.

Процесс систематизации или упорядочения,
первичных биометрических данных в целях
извлечения заключенной в них информации,
обнаружения
закономерности,
которой
следует изучаемое явление или процесс
называется группировкой. Она может быть
простой и сложной.
Группировка по одному признаку называется
простой (простая таблица), по нескольким
признакам - сложной (корреляционная
таблица).

15.

Статистические оценки
генеральных параметров.

16.

Так как
характеристикой варьирования
оценок около своего среднего может быть
стандартное
отклонение,
то
применительно к оценкам его называют
ошибкой оценки.
Учитывая, что размер этой ошибки является
функцией
объема
выборки,
соответствующие
ошибки
получили
название ошибок выборочности или
ошибок репрезентативности.

17.

Равенство или неравенство математических
ожиданий оценок и соответствующих им
констант служит критерием для
определения качества ошибок, которое
получило название смещенности.

18. Требования, предъявляемые к оценкам

Состоятельность
• Точечные
оценки
называют
состоятельными,
если
при
увеличении
числа
испытаний
(n→∞) они стремятся к величине
оцениваемых
параметров.
Для µ - x и σ² - Sx²
Несмещенность
• Если математические ожидания
при любом объеме выборки
равны
оцениваемому
параметру или константе, то
такие
оценки
называют
несмещенными.

19. Ошибка репрезентативности (для среднего)

Ошибка репрезентативности
Sx
Sx
n
Sx
n
Sx
(x )
x n
2
Sx
2
(для среднего)
( x x)
2
i
n(n 1)
2
(
x
)
i
2
x
i
n
Sx
n(n 1)
2
i
i
n(n 1)
Sx
2
2
1 xi xi
n 1 n
n

20. Если средняя арифметическая вычисляется способом условной средней ее ошибка определяется как:

1 pa pa
n 1 n
n
2
Sx
2

21. ФОРМУЛА ОШИБКИ ВЫБОРОЧНОЙ СРЕДНЕЙ ПРИ БЕСПОВТОРНОЙ ВЫБОРКЕ

sx N n
N n
Sx
n N 1
n N 1
sx
2

22. Показатель точности определения средней

CS
Sx
x
100%
CS
%
n

23. Ошибка выборочной доли

p(100 p)
S pf
n
S pf
p(1 p)
n

24. Определение объема выборки

2
t Sx
n
2
2

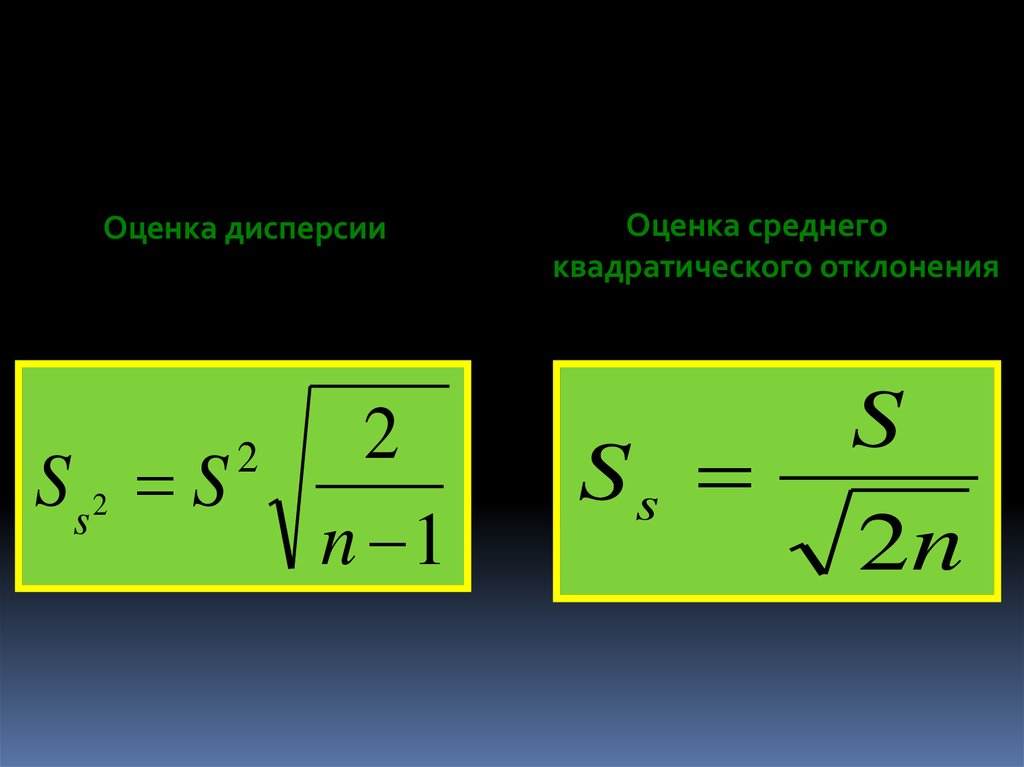
25.

Оценка дисперсии
Ss2 S
2
2
n 1
Оценка среднего
квадратического отклонения
Ss
S
2n

26.

Оценка коэффициента
вариации
2
0,5
100
S
n
0,5 0,0001 2
n
или
S
2n

27.

Оценка медианы
S med
S
c
n

28.

Интервальные
оценки

29. Вероятности, признанные достаточными, для суждений о генеральных параметрах на основании выборочных показателей называются

доверительными
Р – доверительная вероятность.
При Р=0,95 есть риск ошибиться при оценке генерального параметра 1
раз на 20 испытаний
(Р=0,99 – 1 раз на 100 испытаний, Р=0,999 – 1 раз на 1000 испытаний).
Уровень значимости 0,05; 0,01; 0,001 (вместо Р=0,95)
Каждой доверительной вероятности соответствует своя величина
нормированного отклонения t.
P1 0, 95..................t1 1, 96
P2 0, 99..................t2 2, 58
P3 0, 999..................t3 3, 29

30.

Здесь при Р=0,95 есть риск ошибиться при
оценке генерального параметра 1 раз на 20
испытаний
(Р=0,99 – 1 раз на 100 испытаний, Р=0,999 – 1
раз на 1000 испытаний).
Уровень значимости 0,05; 0,01; 0,001
(вместо Р=0,95)
Каждой
доверительной
вероятности
соответствует
своя
величина
нормированного отклонения t.

31. Нормированное отклонение – показатель представляющий отклонение той или иной варианты от средней величины, отнесенное к

величине среднего квадратического отклонения.
xi x
t
Sx
t
xi

32.

Вероятность отклонения любой варианты (хi)
нормально распределяющейся
совокупности от центра распределения (μ)
определяется функцией и нормированного
отклонения (t), и доверительный интервал
для неизвестного параметра будет равен:

33. Доверительный интервал

xi
t
t
sx
х tSх
S
S
x t
x t
N
N

34.

S
S
2
2
S t
S t
2n
2n
2

35. Спасибо за внимание!