Скалярное произведение векторов

1.

Скалярное
произведение векторов

2.

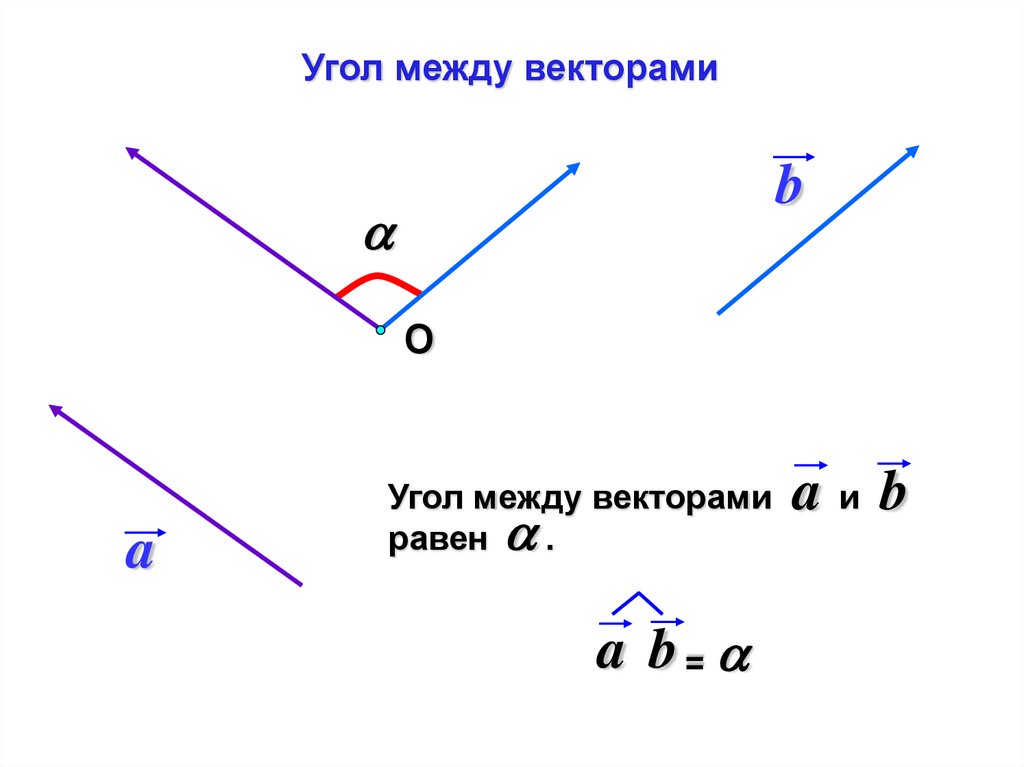
Угол между векторами
b
О
a
Угол между векторами
равен .
a b =
aиb

3.

Определение
Скалярным произведением двух
векторов называется произведение
их длин на косинус угла между ними.
a b = a b cos(a b )
Скалярное произведение векторов – число
(скаляр).

4.

Частный случай №1
b
a
a b = 900
a b = a b cos 900 = 0
Скалярное произведение ненулевых
векторов равно нулю тогда и только тогда,
когда эти векторы перпендикулярны.
a b = 0
a b

5.

Частный случай №2
a b < 900
b
a
a b = a b cos > 0
Скалярное произведение ненулевых векторов
положительно тогда и только тогда, когда угол
между векторами острый.
a b > 0 a b < 900

6.

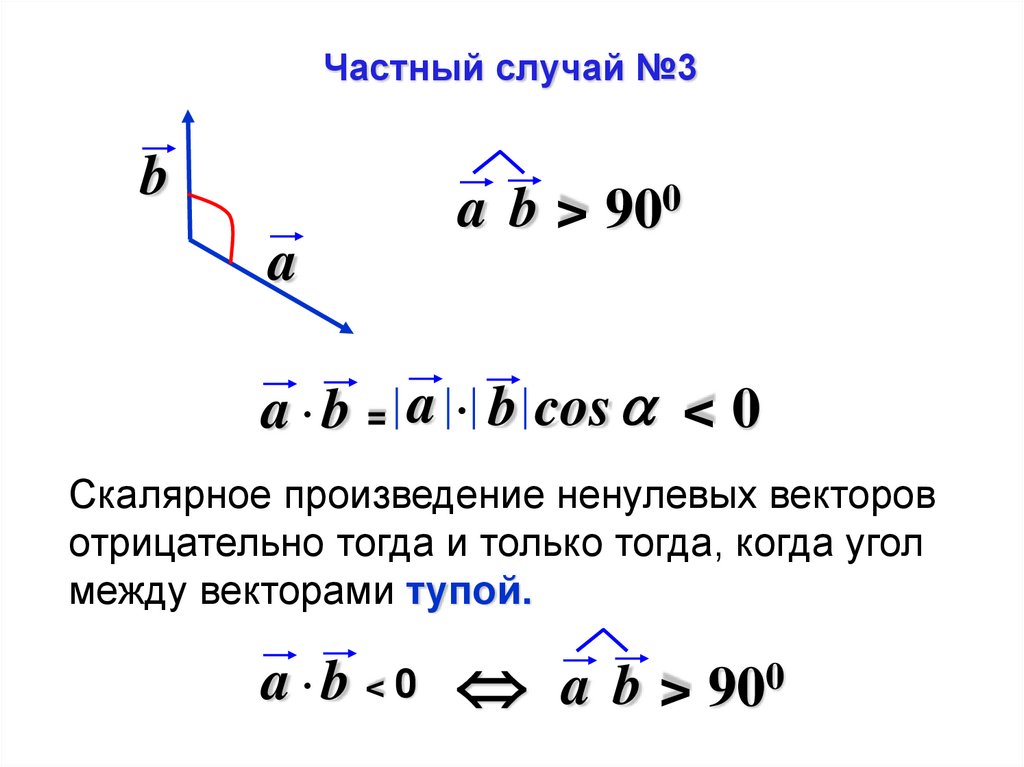
Частный случай №3
b
a b > 900
a
a b = a b cos < 0
Скалярное произведение ненулевых векторов
отрицательно тогда и только тогда, когда угол
между векторами тупой.
a b < 0 a b > 900

7.

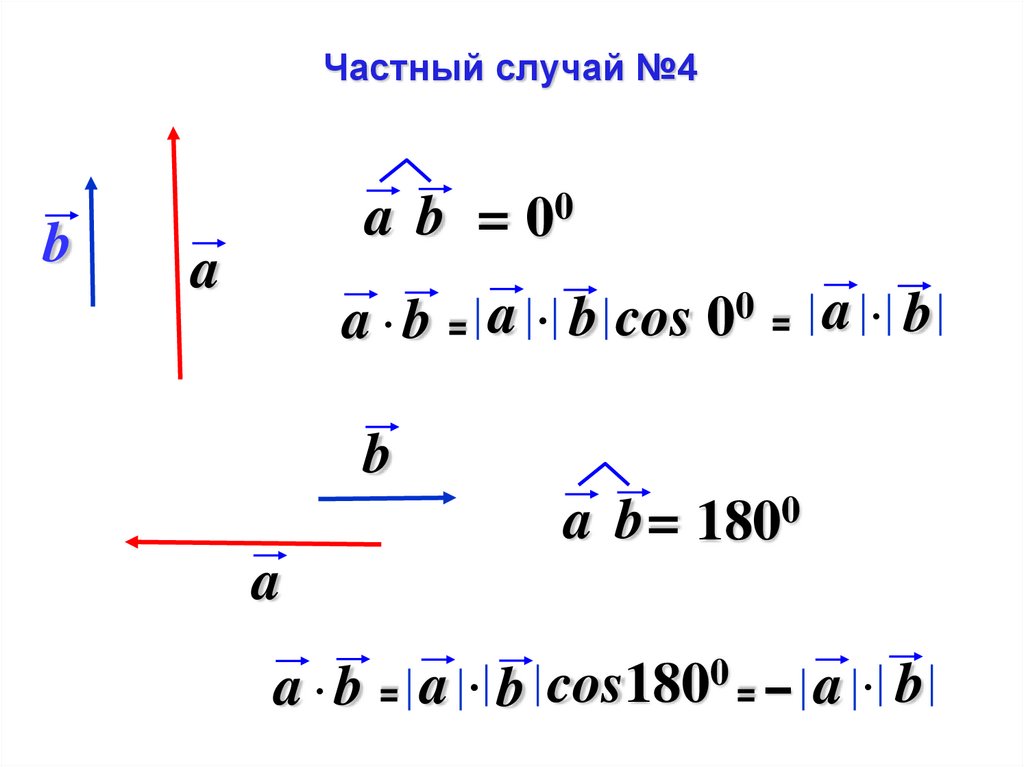
Частный случай №4
b
a b = 00
a
a b = a b cos 00 = a b
b
a b = 1800
a
a b = a b cos1800 = – a b

8.

Частный случай №5
a a = 00
a
1
2
a a = a a cos 00 = a a = a
a a называется
2
скалярным квадратом вектора a и обозначается a
Скалярное произведение
Таким образом,
скалярный квадрат вектора равен квадрату его длины.
2
a =a
2

9.

Формула для нахождения
скалярного произведения
через координаты векторов
a = x1 i + y 1 j + z 1 k
a b= ?
b = x2 i + y 2 j + z 2 k
a b= (x1 i + y1 j + z1 k) (x2 i + y2 j + z2 k) =
= x1x2 + y1y2 + z1z2
a b = x1x2 + y1y2 + z1z2

10.

Формула для нахождения
скалярного произведения
через координаты векторов

11.

Пример №1
Найти скалярное произведение векторов:
a {-6; 9; 5}
b {-1; 0; 7}
a b= x1x2 + y1y2 + z1z2
a b= -6 (-1) + 9 0 + 5 7 = 41