Похожие презентации:
Скалярное произведение векторов
1.
2.
ДОМАШНЕЕ ЗАДАНИЕ§2, п.46,47,48
стр. 116, в.11, 12, 14 – устно
№ 441 (а,б,д,ж,з)
№ 444
№ 445 (а)
3.
ПОВТОРЕНИЕ ИЗУЧЕННОГОВектор – направленный отрезок.
4.
5.
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕВЕКТОРОВ
6.
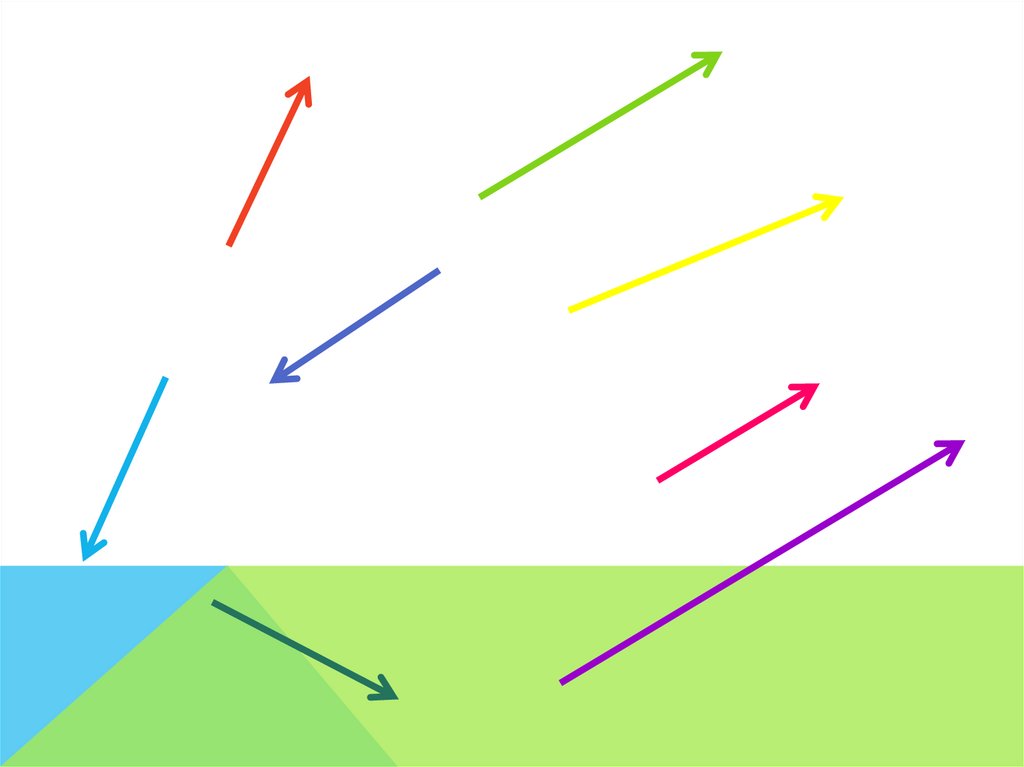
Угол между векторамиb
О
a
7.
ОПРЕДЕЛЕНИЕУглом между любыми двумя
ненулевыми векторами
называется угол между
равными им векторами с
общим началом.
8.
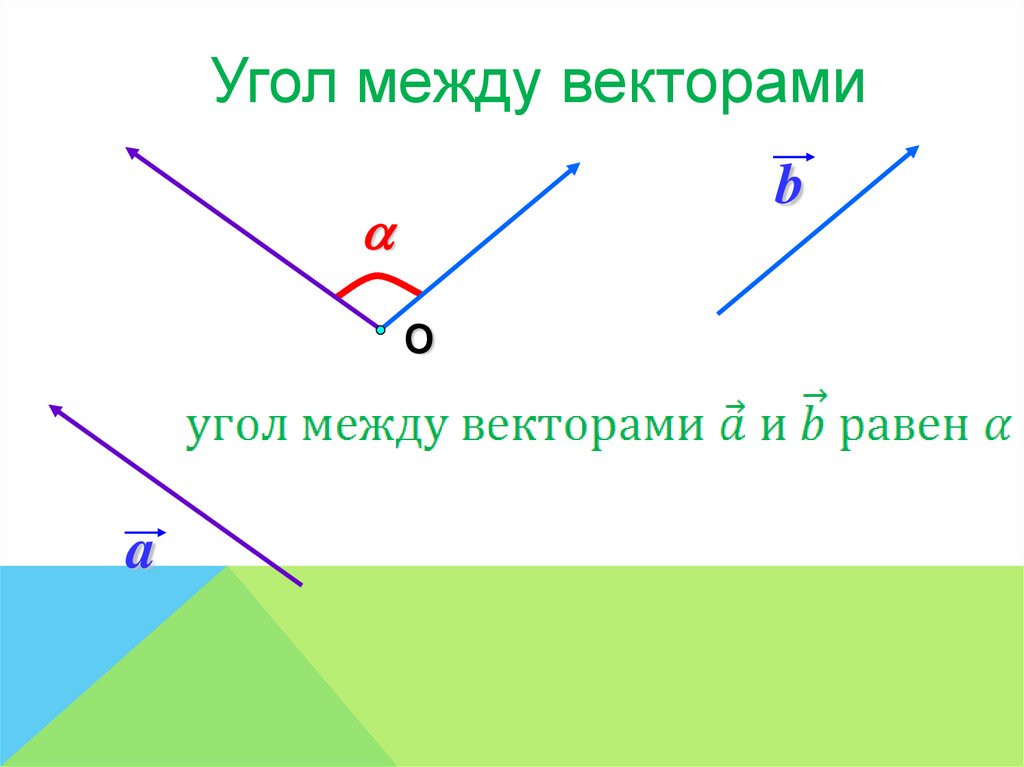
Найдите угол междувекторами
a
a c = 1200
d
300
c
a b = 300
b
f
b c = 900
d c = 1800
d f = 00
9.
ОпределениеСкалярным произведением двух
векторов называется произведение
их длин на косинус угла между ними.
a b = a b cos( a b)
Скалярное произведение векторов
– число (скаляр)
10.
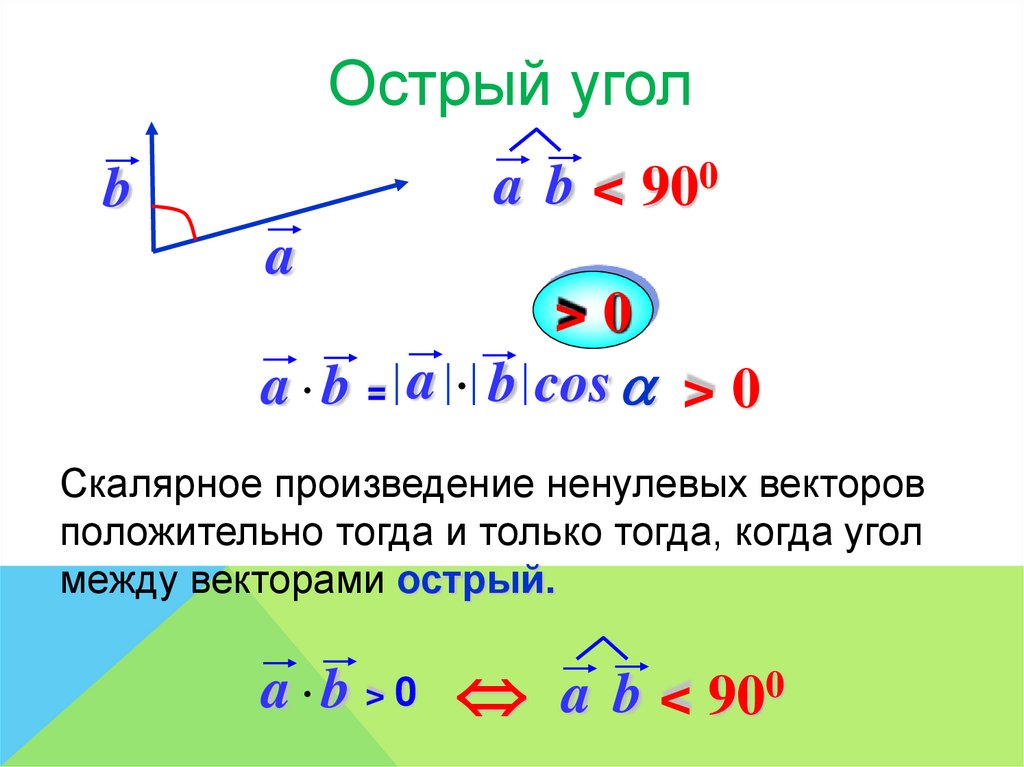
Острый уголa b < 900
b
a
>0
a b = a b cos > 0
Скалярное произведение ненулевых векторов
положительно тогда и только тогда, когда угол
между векторами острый.
a b > 0 a b < 900
11.
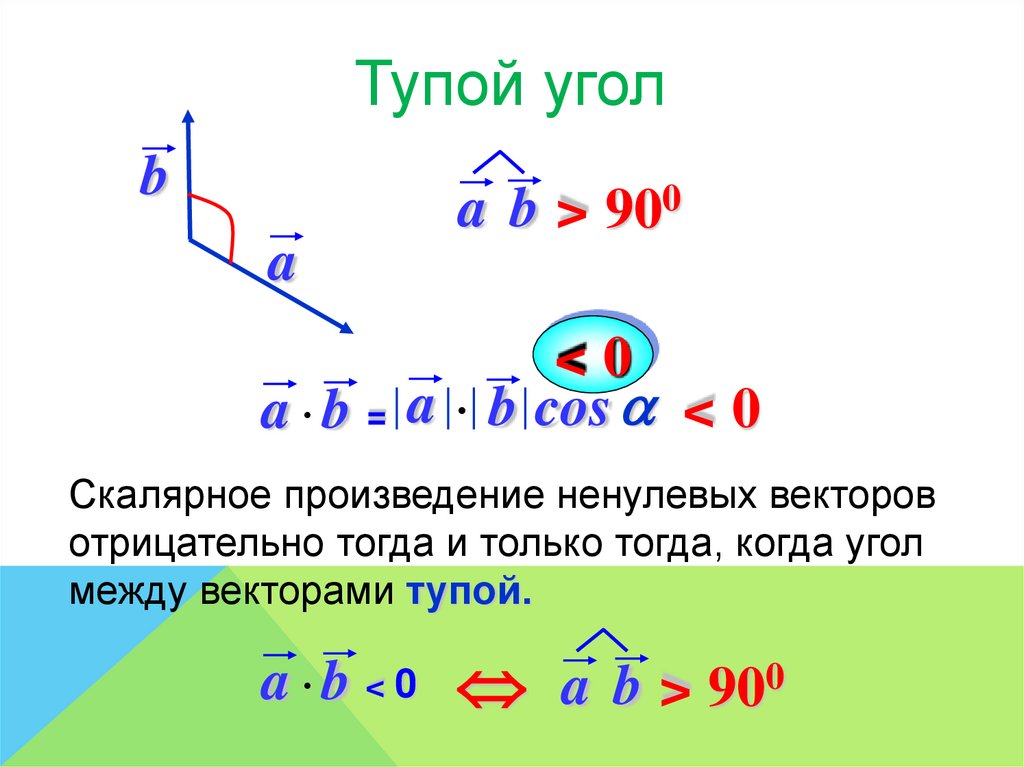
Тупой уголb
a b > 900
a
<0
a b = a b cos < 0
Скалярное произведение ненулевых векторов
отрицательно тогда и только тогда, когда угол
между векторами тупой.
a b < 0 a b > 900
12.
Прямой уголb
a
a b = 900
=0
a b = a b cos 900 = 0
Скалярное произведение ненулевых векторов
равно нулю тогда и только тогда, когда эти
векторы перпендикулярны.
a b = 0
a b
13.
Частный случайb
a b = 00
1
a b = a b cos 00 = a b
a
b
a b = 1800
a
-1
a b = a b cos1800 = – a b
14.
Скалярный квадратa a = 00
a
1
2
a a = a a cos 00 = a a = a
a a называется
2
скалярным квадратом вектора a и обозначается a
Скалярное произведение
скалярный квадрат вектора равен квадрату его длины.
2
a =a
2
15.
Скалярное произведениекоординатных векторов
16.
ЗадачаВсе ребра тетраэдра АВСD равны друг другу. Точки М и
N – середины ребер АD и ВС. Докажите, что MN AD = 0
A
M
D
B
N
C
17.
НАЙТИСКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ
a {-6; 9; 5}
b {-1; 0; 7}
?
18.
Формула для нахожденияскалярного произведения
через координаты векторов
a = x1 i + y1 j + z 1 k
a b= ?
b = x2 i + y2 j + z 2 k
a b= (x1 i + y1 j + z1 k) (x2 i + y2 j + z2 k) =
= x1x2 + y1y2 + z1z2
a b = x1x2 + y1y2 + z1z2
19.
Найтискалярное произведение
a {-6; 9; 5}
b {-1; 0; 7}
a b= x1x2 + y1y2 + z1z2
a b= -6 (-1) + 9 0 + 5 7 = 41
20.
Найтискалярное произведение
a {0; 0; 4}
b {22; 1; 8}
a b= x1x2 + y1y2 + z1z2
a b= 0 22 + 0 1 + 4 8 = 32
21.
Найтискалярное произведение
a {1; 7; 9}
b {-2; 4; 0}
a b= x1x2 + y1y2 + z1z2
a b = 1 (-2) + 7 4 + 9 0 = 26
22.
РАБОТА С УЧЕБНИКОМ№ 441 (в,г,е)
№ 448 (а)
23.
ДОМАШНЕЕ ЗАДАНИЕ§2, п.46,47,48
стр. 116, в.11, 12, 14 – устно
№ 441 (а,б,д,ж,з)
№ 444
№ 445 (а)



















 Математика
Математика