Похожие презентации:
Основы теории фракталов
1. Основы теории фракталов
Домашних И.А.2. Геометрия природы
Рождение фрактальной геометрии принято связыватьс выходом в 1977 году книги Мандельброта
"The Fractal Geometry of Nature" ("Фрактальная геометрия природы")
3. Природные фракталы
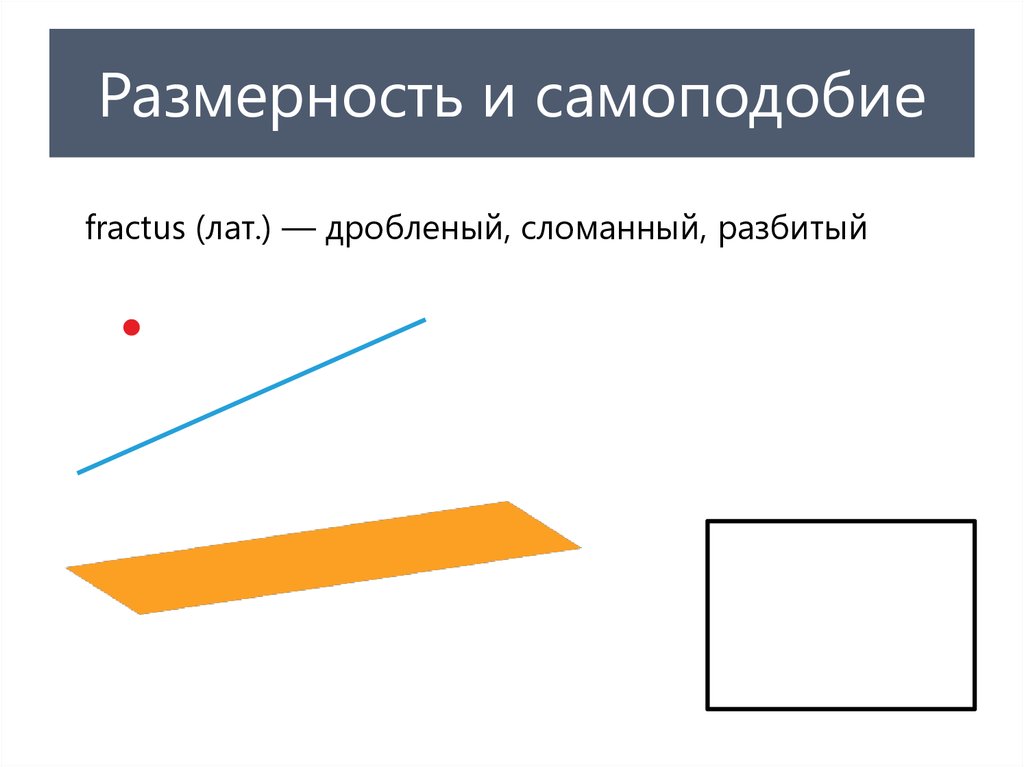
4. Размерность и самоподобие
fractus (лат.) — дробленый, сломанный, разбитый5. Патологические структуры
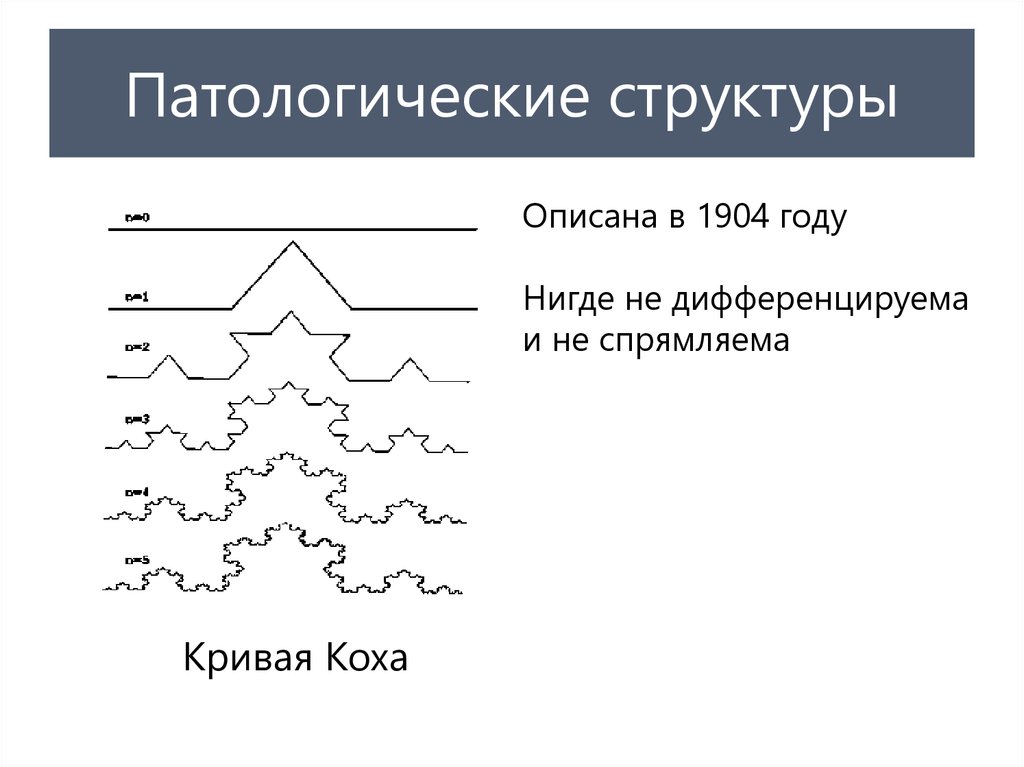
Описана в 1904 годуНигде не дифференцируема
и не спрямляема
Кривая Коха
6. Определение
Фрактал (лат. fractus — дробленый, сломанный,разбитый) — термин, означающий сложную
геометрическую фигуру, обладающую свойством
самоподобия, то есть составленную из нескольких
частей, каждая из которых подобна всей фигуре
целиком
Фракталом называется структура, состоящая из частей,
которые в каком-то смысле подобны целому
(Мандельброт)
7. Свойства
СамоподобиеДробная размерность (в смысле Минковского или
Хаусдорфа)
8. Геометрические фракталы
Самые наглядныеВ двумерном случае их получают с помощью некоторой
ломаной, называемой генератором
За один шаг алгоритма каждый из отрезков,
составляющих ломаную, заменяется на генератор, в
соответствующем масштабе
В результате бесконечного повторения этой процедуры,
получается геометрический фрактал
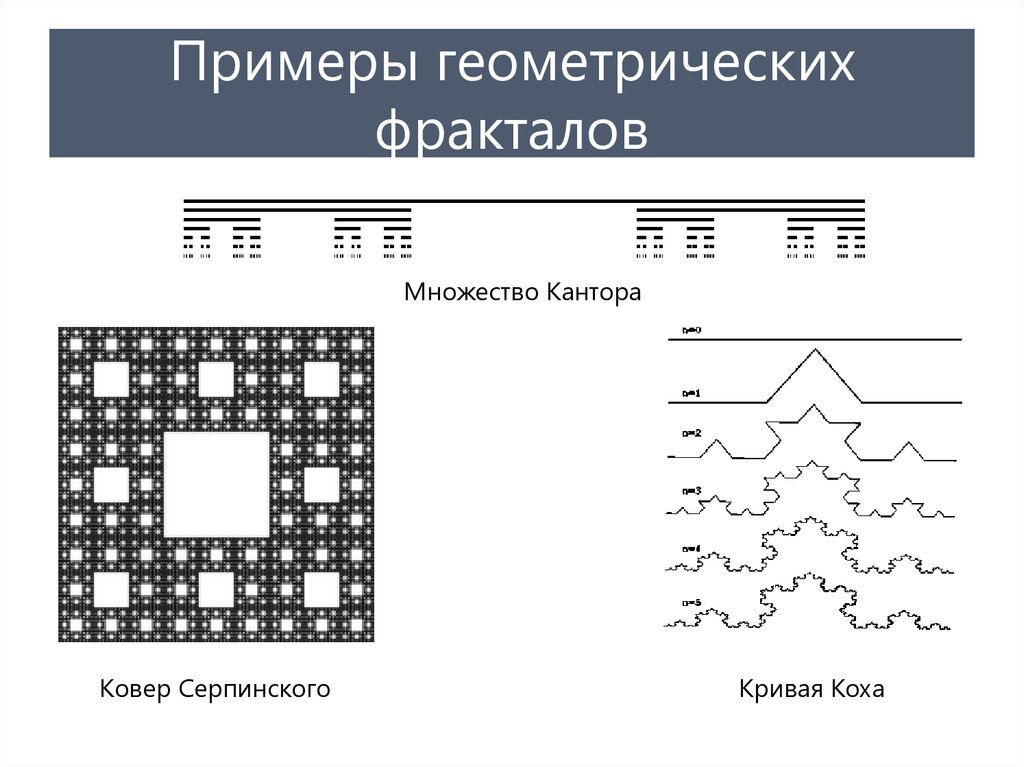
9. Примеры геометрических фракталов
Множество КантораКовер Серпинского
Кривая Коха
10. Алгебраические фракталы
Для построения используются итерации нелинейныхотображений, задаваемых простыми алгебраическими
формулами














 Математика
Математика Информатика
Информатика








