Похожие презентации:
Фракталы. Историческая справка
1.
ФРАКТАЛЫАвтор: Касьянова Светлана
ученица 10б класса
МАОУ «СОШ №19» г. Перми
2.
Многие природные объекты и явления имеютфрактальную форму или обладают фрактальными
свойствами.
3.
4.
Историческаясправка
5.
Фрактал (лат. fractus —дробленый, сломанный,
разбитый) —
термин, означающий
геометрическую фигуру,
обладающую свойством
самоподобия.
6.
Звезда КохаОдин из первых примеров
фракталов был придуман еще в
начале 20-го века немецким
математиком Хельгой фон Кох
(1870-1924) и называется
звезда Кох.
7.
В результате получаются все более сложныемногоугольники, приближающиеся к
предельному положению – звезде Кох.
8.
СалфеткаЕще один вариант звезды Кох можно построить из
квадратов,
последовательным
добавлением
к
исходному квадрату подобных ему квадратов.
9.
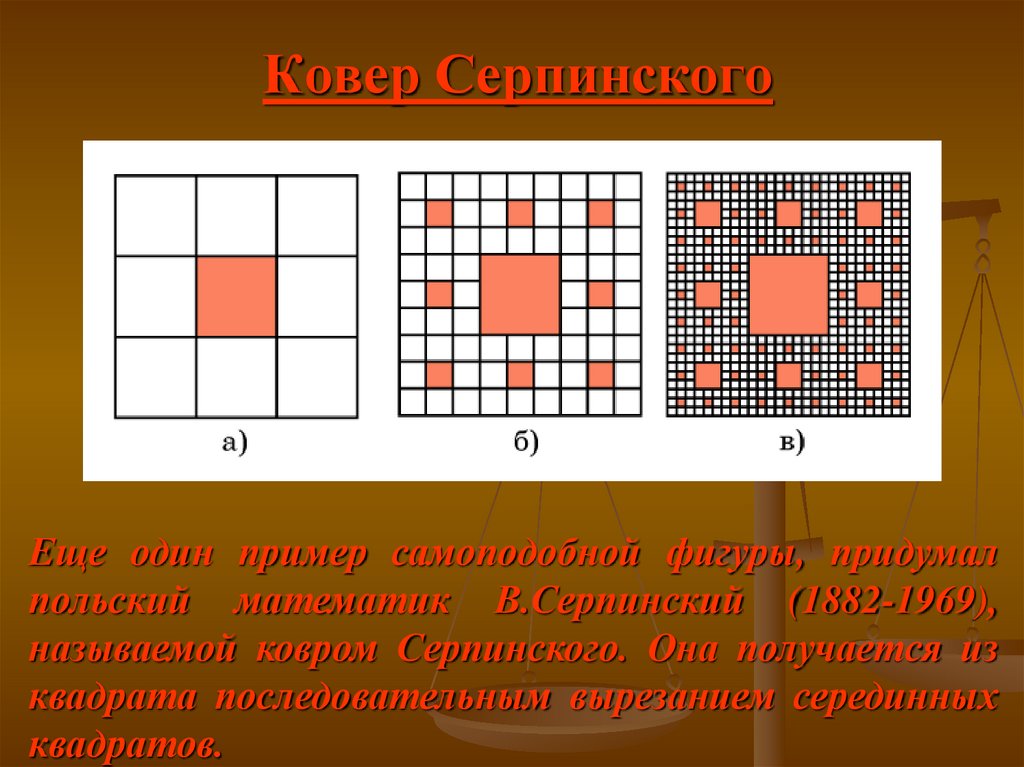
Ковер СерпинскогоЕще один пример самоподобной фигуры, придумал
польский математик В.Серпинский (1882-1969),
называемой ковром Серпинского. Она получается из
квадрата последовательным вырезанием серединных
квадратов.
10.
Начиная не с квадрата, а с правильного треугольника,и вырезая центральные треугольники, получим
самоподобную фигуру, аналогичную ковру Серпинского
и называемую салфеткой Серпинского.
Салфетка Серпинского
11.
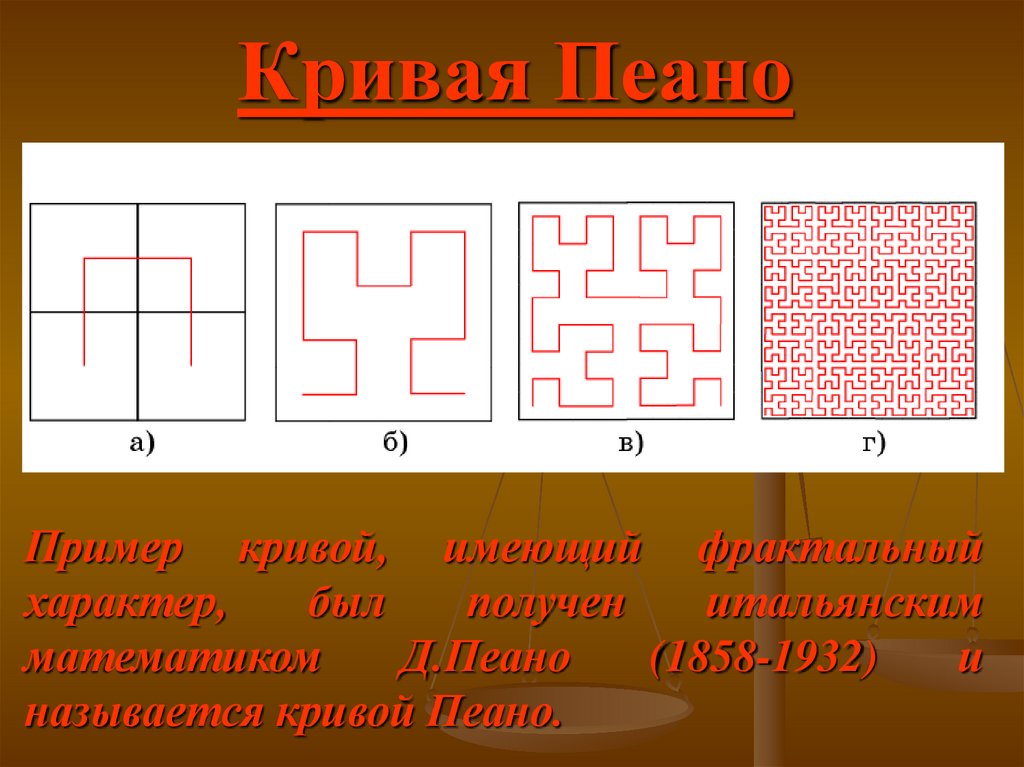
Кривая ПеаноПример кривой, имеющий фрактальный
характер,
был
получен
итальянским
математиком
Д.Пеано
(1858-1932)
и
называется кривой Пеано.
12.
Интересным примером самоподобной кривойявляется «Кривая дракона», придуманная физиком
Джон Хейтуэй.
Кривая дракона
13.
Структурафрактала
14.
В последние двадцать пять лет возникло иразвивается новое направление в
математике – фрактальная геометрия.
Термин «фрактал» был введён франко –
американским математиком Бенуа
Мандельбротом в 1975 году и получил
широкую популярность с выходом в 1977
году его книги «Фрактальная геометрия
природы».
15.
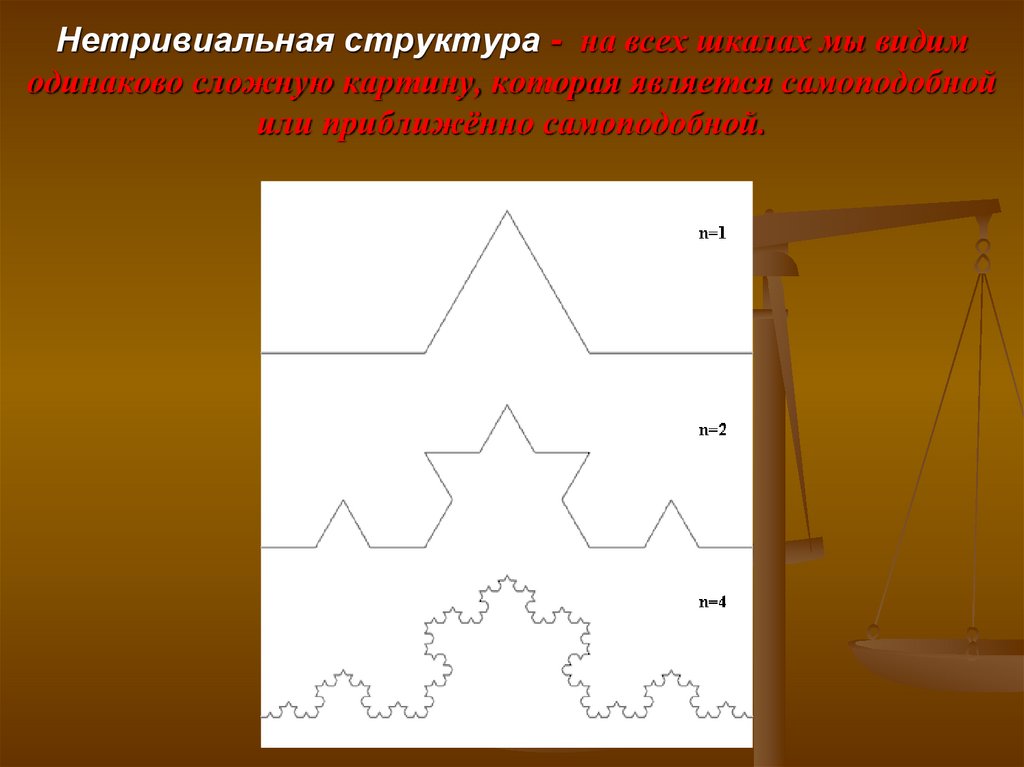
Нетривиальная структура - на всех шкалах мы видимодинаково сложную картину, которая является самоподобной
или приближённо самоподобной.
16.
17.
Дерево ПифагораКонструктивный фрактал - это множество,
получающееся в результате линейных сжимающих
отображений подобия
18.
19.
СалфеткаСалфетка строится из кругов,
последовательным добавлением к
исходному кругу подобных ему кругов.
20.
21.
Исследовательскаяработа
22.
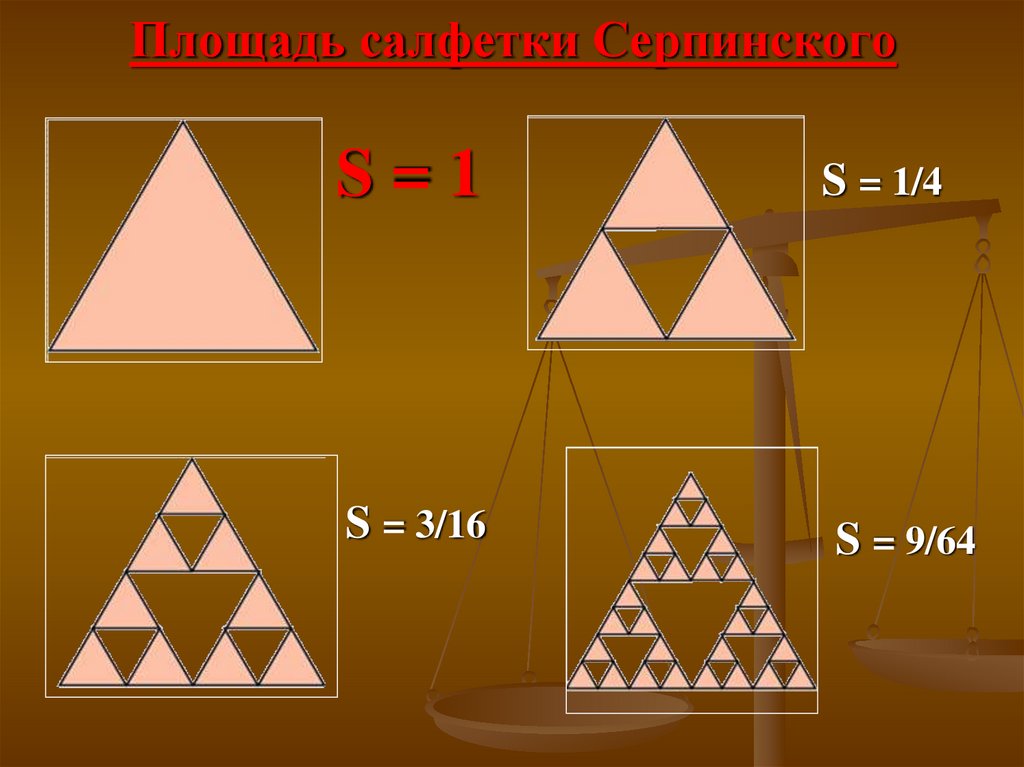
Площадь салфетки СерпинскогоS=1
S = 1/4
S = 3/16
S = 9/64
23.
Бесконечная геометрическая прогрессия: 1/4, 3/16, 9/64, 27/256и т.д. с начальным членом b1=1/4 и знаменателем q=3/4.
S = 27/256
По формуле суммы геометрической прогрессии S = b1 ( ׃1 – q)
находим площадь вырезаемой части:
S = 1/4 ( ׃1 – 3/4) = 1/4 ׃1/4 = 1.
Получаем, что площадь салфетки Серпинского равна
S = 1 - 1 = 0.
24.
25.
Фракталывокруг нас
26.
В последние 20 лет фракталыстали очень популярны.
Лепестки роз
Фрактальная форма
подвида цветной капусты
27.
Листья деревьев28.
Трещины в некоторых породах29.
В космонавтике30.
Зимние узоры на стекле31.
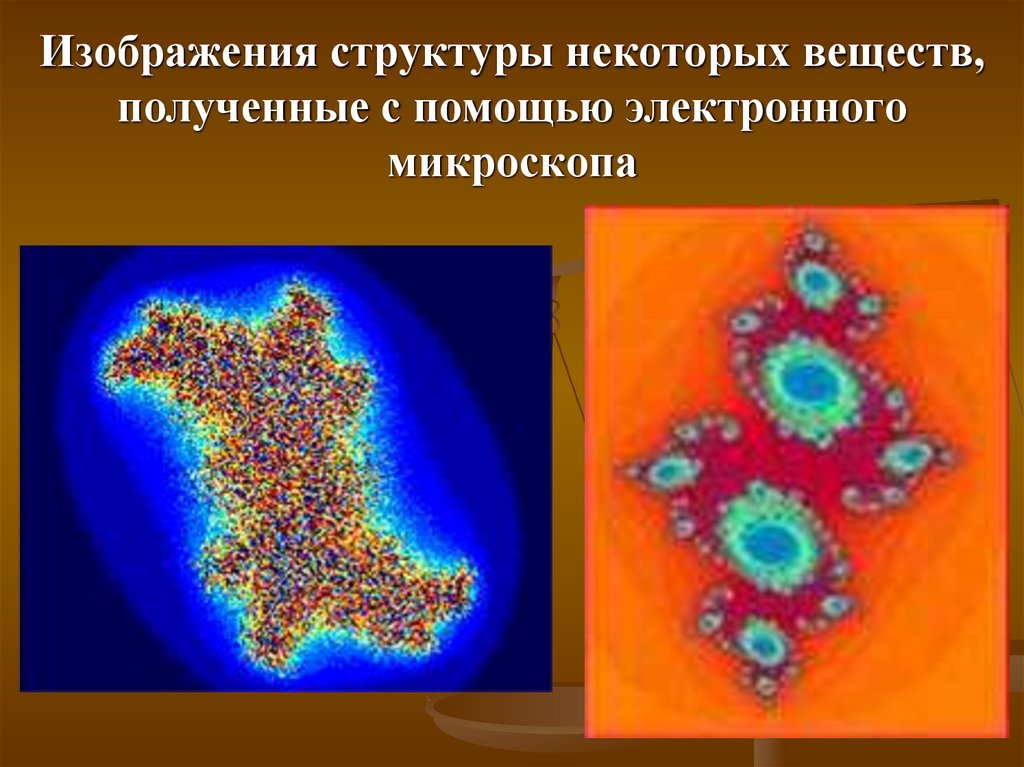
Изображения структуры некоторых веществ,полученные с помощью электронного
микроскопа
32.
Турбулентные потоки в жидкостях.33.
В морской тематике34.
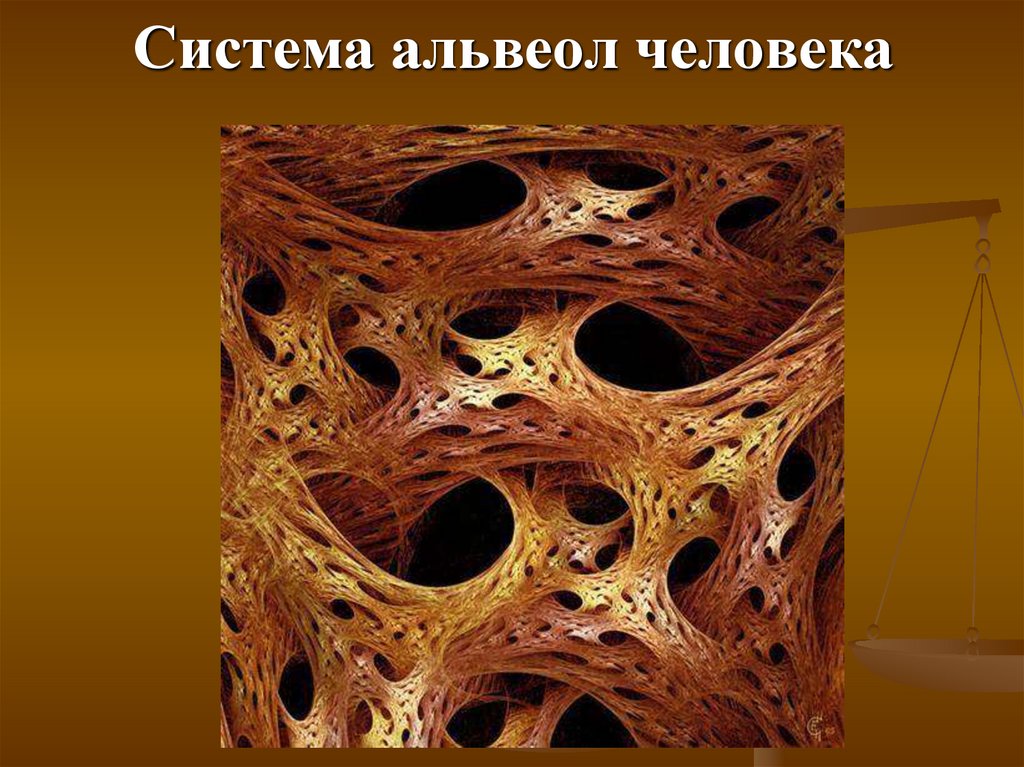
Система альвеол человека35.
В двумерных моделях статистическоймеханики
36.
В компьюторной графике37.
В изобразительном искусстве38.
Фракталы, особенно наплоскости, популярны
благодаря сочетанию
красоты с простотой
построения при помощи
компьютера.
Спасибо за внимание





























 Математика
Математика








