Похожие презентации:
Координаты точки. Координаты вектора
1.
2015 г2.
Цели урока:Образовательная:
Изучить понятие о прямоугольной системе
координат, координатах точки и координатах
вектора.
Развивающая:
Развивать математические способности, память,
устную и письменную математическую речь и
пространственное воображение.
Воспитательная:
Воспитывать интерес к предмету, внимательность,
сосредоточенность, аккуратность,
доброжелательное отношение друг к другу.
3.
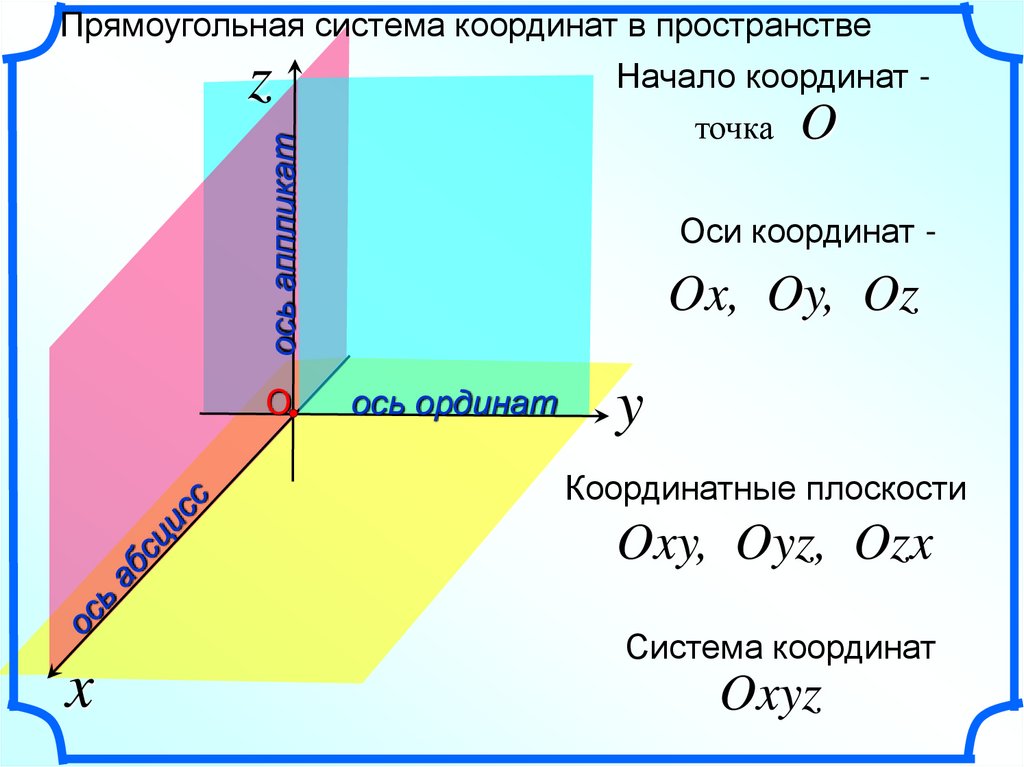
Прямоугольная система координат в пространствеНачало координат точка O
ось аппликат
z
О
Оси координат -
Ox, Oy, Oz
ось ординат
y
Координатные плоскости
Oxy, Oyz, Ozx
x
Система координат
Oxyz
4.
Положительная полуосьz
x
Отрицательная полуось
Отрицательная полуось О
Положительная полуось
y
Луч, направление
которого совпадает
с направлением
оси, называется
положительной
полуосью,
а другой луч –
отрицательной
полуосью
5.
Координаты точкиВ прямоугольной
системе координат
каждой точке М
пространства
сопоставляется тройка
чисел, которые
называются
координатами точки
z
M3
M(x; y; z)
О
M1
x
M2
y
M (x; y; z)
x = OM1
абсцисса
y = OM2
ордината
z = OM3
аппликата
6.
zI
O (0; 0; 0)
N (5; 0; 0)
I
D
I
I
F (0; -2; 0)
I
D(0; 0; 4)
I
F
I
I
О
I
M
I
I
I
I
y R(0; 0; -0,5)
S(x; 0; 0) Ox
I
N
I
I
R
I
x
P(0; y; 0) Oy
T(0; 0; z) Oz
M(0; 3; 0)
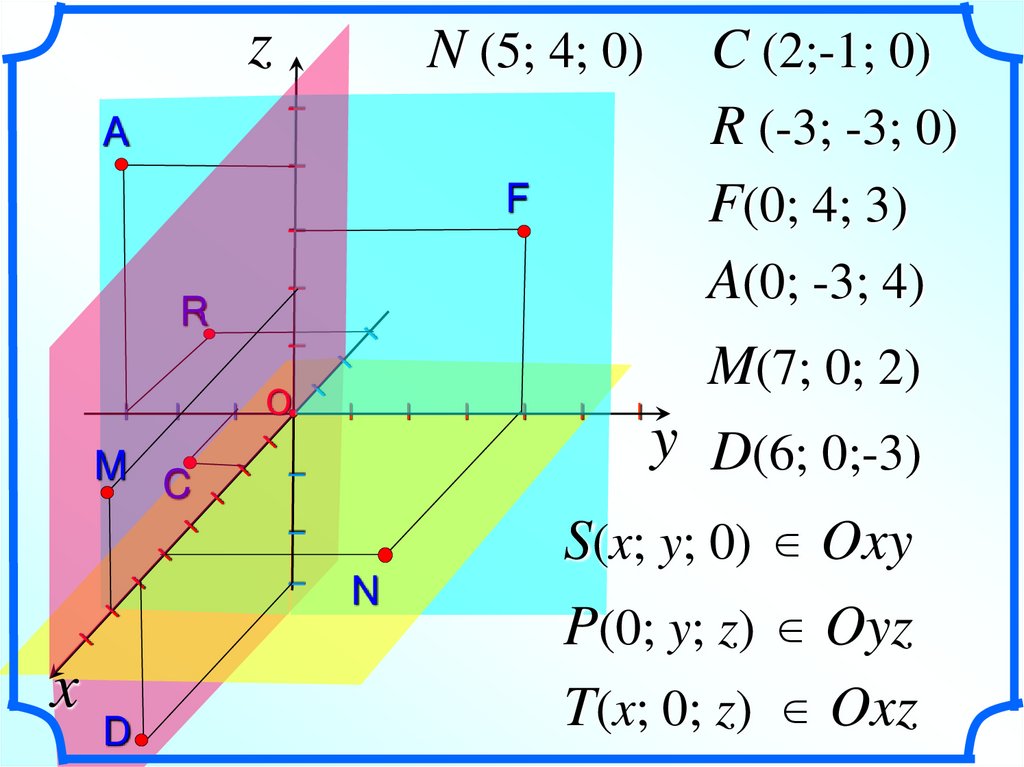
7.
zI
N (5; 4; 0)
I
A
I
I
F
I
R
I
О
I
I
x
D
I
I
I
I
I
y D(6; 0;-3)
S(x; y; 0) Oxy
I
M C
I
M(7; 0; 2)
I
I
C (2;-1; 0)
R (-3; -3; 0)
F(0; 4; 3)
A(0; -3; 4)
N
P(0; y; z) Oyz
T(x; 0; z) Oxz
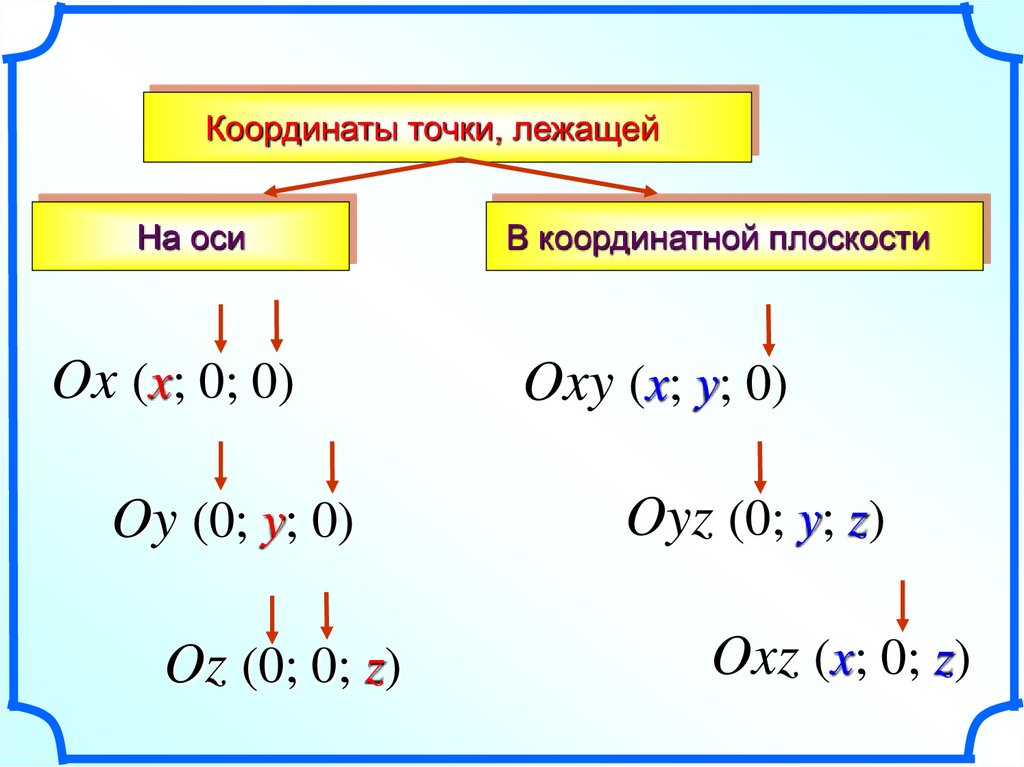
8.
Координаты точки, лежащейНа оси
Ox (x; 0; 0)
Oy (0; y; 0)
Oz (0; 0; z)
В координатной плоскости
Oxy (x; y; 0)
Oyz (0; y; z)
Oxz (x; 0; z)
9.
zA (4;-2,5; 7)
S
I
I
A
R
I
S (5; 4; 8)
I
I
I
I
N
I
I
I
I
I
I
D (5; 4;-3)
I
I
I
I
О
I
I
I
I
I
I
y
N(0; 0; 4)
R(-2;-3; 4)
I
I
I
I
I
I
I
I
I
I
I
I
I
I
I
I
I
I
F(-3; 3;-7)
I
C
I
I
I
x M
I
M(7; 0;-1)
D
F
C(7; 4;-1)
10.
Задание!z
A
B
D
E
O
C
x
F
y
11.
Ответы.1. A(5; 4; 10),
2. B(4; -3; 6),
3. C(5; 0; 0),
4. D(4; 0; 4),
5. E(0; 5; 0),
6. F(0; 0; -2).
Сравни свои ответы.
12.
Критерии оценки:• Без ошибок- «5»
• 1 ошибка – «4»
• 2-3 ошибки – «3»
• Более 3 ошибок – «2»
13.
zI
a
a = xi + yj + zk
I
I
I
I
I
j
y
I
I
i
O
I
I
разложение вектора по
координатным векторам
I
I
I
F
k
I
i, jи k
I
I
i =1;
j =1;
k =1
Координаты вектора
– координатные векторы
x
a{ x; y; z} координаты вектора
F(x; y; z)
14.
zВектор, начало которого
совпадает с началом
координат – радиус-вектор.
I
I
I
S
I
I
I
I
j
I
I
I
I
y
S(4; 5; 8)
p {4; 5; 8}
I
I
I
i
O
I
I
I
I
I
k
I
I
I
I
p
Координаты радиус-вектора
совпадают с координатами
конца вектора.
x
p =4i +5j +8k
15.
zI
R
OT {4; 5; 0}
I
I
D
OF {-1; 3;-6}
I
I
I
I
I
OD {-1; 3; 3}
I
I
i
I
I
I
I
j
I
y
OE {6; 0; 3}
ON {0; -3; 0}
T
OR {-2; -3; 4}
I
I
I
I
I
E
O
I
NI
I
k
I
I
OM {5; 0; 0}
x
I
M
F
0 {0;0;0}
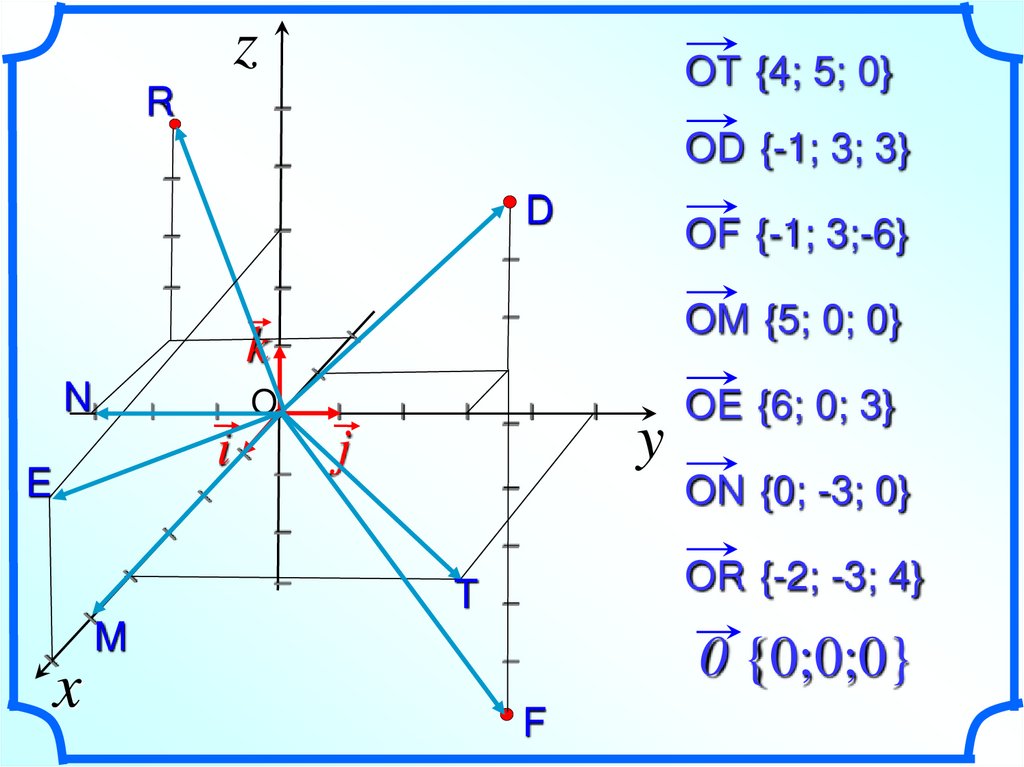
16.
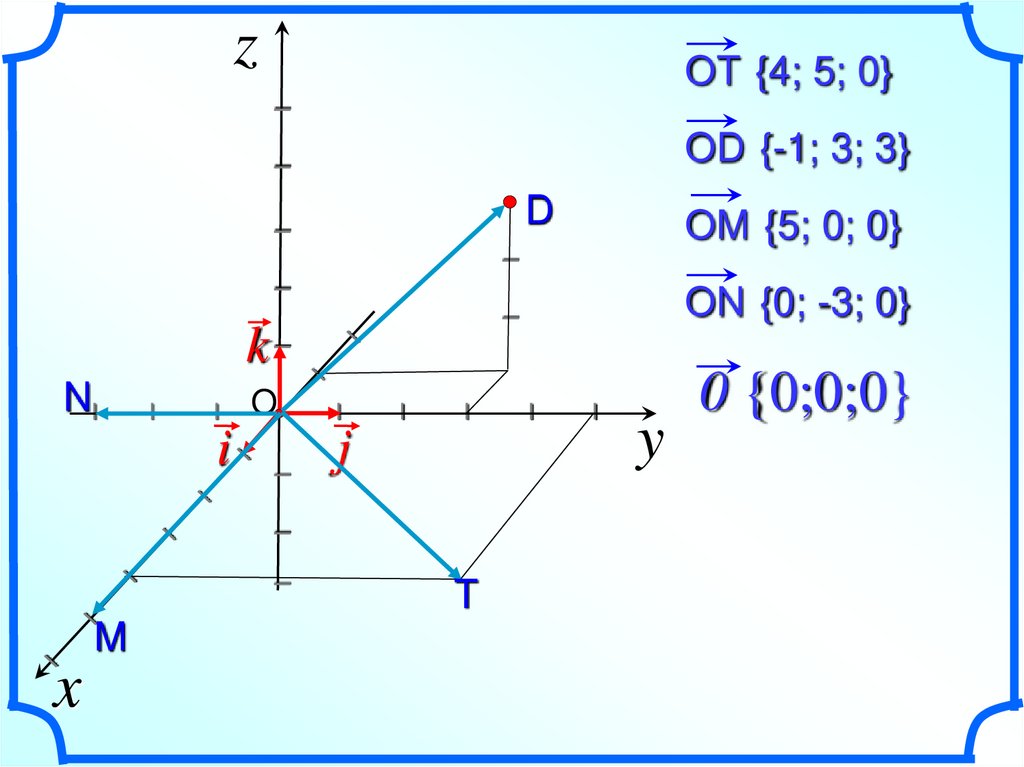
zI
OT {4; 5; 0}
I
OD {-1; 3; 3}
OM {5; 0; 0}
I
I
I
D
k
I
I
I
I
I
j
I
I
i
O
I
NI
I
I
ON {0; -3; 0}
M
x
T
I
I
y
0 {0;0;0}
17.
Координаты вектораa {-6; 9; 5}
n {-8; 0; 1}
c {0; -7; 0}
m{4; 0; 0}
r {-5;-8; 3}
s {-7; 1; 0}
e {0;3; 21}
q {0; 0; 2}
Разложение вектора по
координатным векторам
a = – 6i+9j+5k
n = – 8i+k
c = –7j
m =4i
r = –5i –8j +3k
s = –7i + j
e = 3j +21k
q =2k
18.
Критерии оценки:• Без ошибок- «5»
• 1-2 ошибки – «4»
• 3-4ошибки – «3»
• Более 4 ошибок – «2»
19.
10Каждая координата суммы двух или более
векторов равна сумме соответствующих
координат этих векторов.
Рассмотрим векторы
a {x1;y1;z1}
b {x2;y2;z2}
a +b {x1+x2; y1+y2; z1+z2}
20.
20Каждая координата разности двух векторов равна
разности соответствующих координат этих
векторов.
Рассмотрим векторы
a {x1;y1;z1}
b {x2;y2;z2}
a –b {x1–x2; y1 –y2; z1– z2}
21.
a-bb {-8;12;-3}
Найдите координаты вектора
a {-6; 9;1}
a - b {2;-3; 4}
22.
30Каждая координата произведения вектора на
число равна произведению соответствующей
координаты вектора на это число.
Рассмотрим вектор
a {x; y; z}
a {x; y; z} k
ka {kx; ky; kz}
a {-2; 1;0} 3
3a {-6; 3; 0}
a {-2; 0; 3} (-2)
-2a {4; 0;-6}
23.
Самостоятельнаяработа
24.
ОтветыНа «3»: 1 вариант: 1.С; 2.D; 3.E
2 вариант: 1.C; 2.A; 3.E
На «4»: 1 вариант: 407(г) : d +b {-2,7; 10,1;-0,5}
409(а): a -b {7; -2;1} 409(и): -3b {6; -3;0}
2 вариант: 407(б) : a +c {3 2/3; 10,1;-0,5}
409(в): a -c {5; -1,2; 1} 409(к): -6с {0; -1,2;0}
На «5»:1 вариант: 403(1): a {3; 2;-5}
407(д): d +a {-2,5; -1,9;2,5}
409(б): b -a {-7; 2;-1} 409(м): 0,2b {-0,4; 0,2;0}
2 вариант:
404(1): a =5i -j+2k
407(a): a +b {3; 2;1}
409(г): d -a {-51/3; 32/5;-11/7} 409(з): 2 a {10; -2;2}




















 Математика
Математика








