Похожие презентации:
Координаты вектора
1.
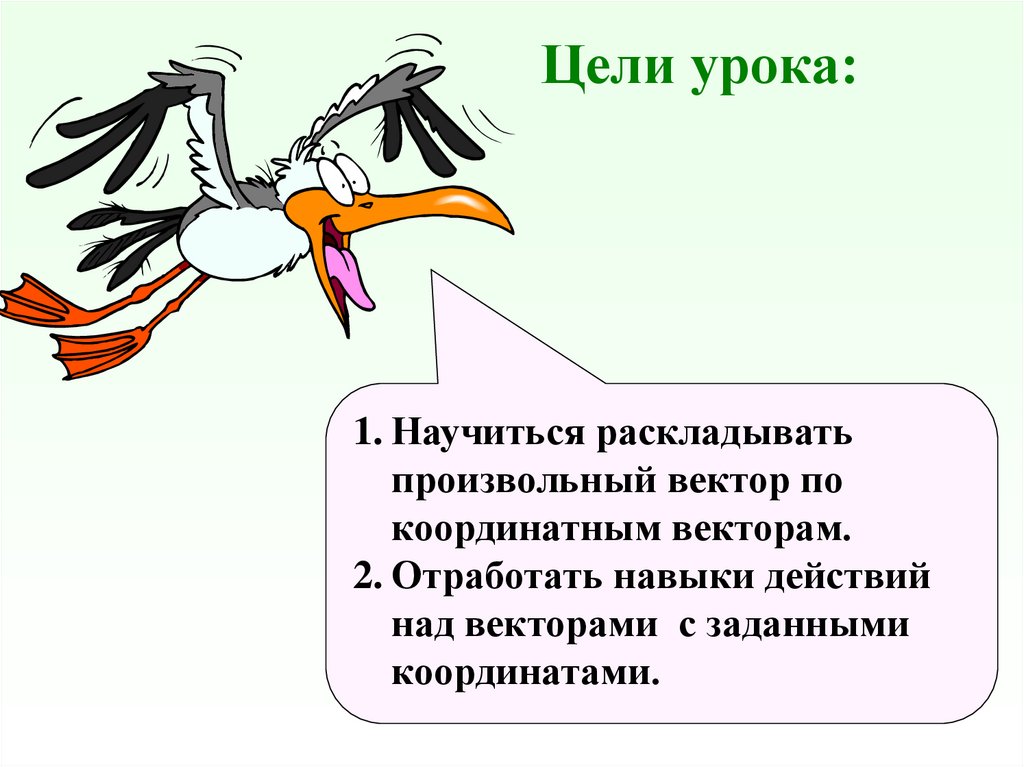
2. Цели урока:
1. Научиться раскладыватьпроизвольный вектор по
координатным векторам.
2. Отработать навыки действий
над векторами с заданными
координатами.
3. Повторение.
Как называются координаты точки впространстве?
К (2; 0; -4)
z
х
у
z
Е (9; -3; 0)
С (2; -6; 3)
Р (0; 5; -7)
х
у
4. Повторение.
Даны точки:А (2; -1; 0)
В (0; 0; -7)
С (2; 0; 0)
D (-4; -1; 0)
Е (0; -3; 0)
F (1; 2; 3)
Р (0; 5; -7)
К (2; 0; -4)
Назовите точки, лежащие
в плоскости Оуz.
Назовите точки, лежащие
в плоскости Охz.
В (0; 0; -7)
Назовите точки, лежащие
в плоскости Оху.
С (2; 0; 0)
Е (0; -3; 0)
5. Повторение.
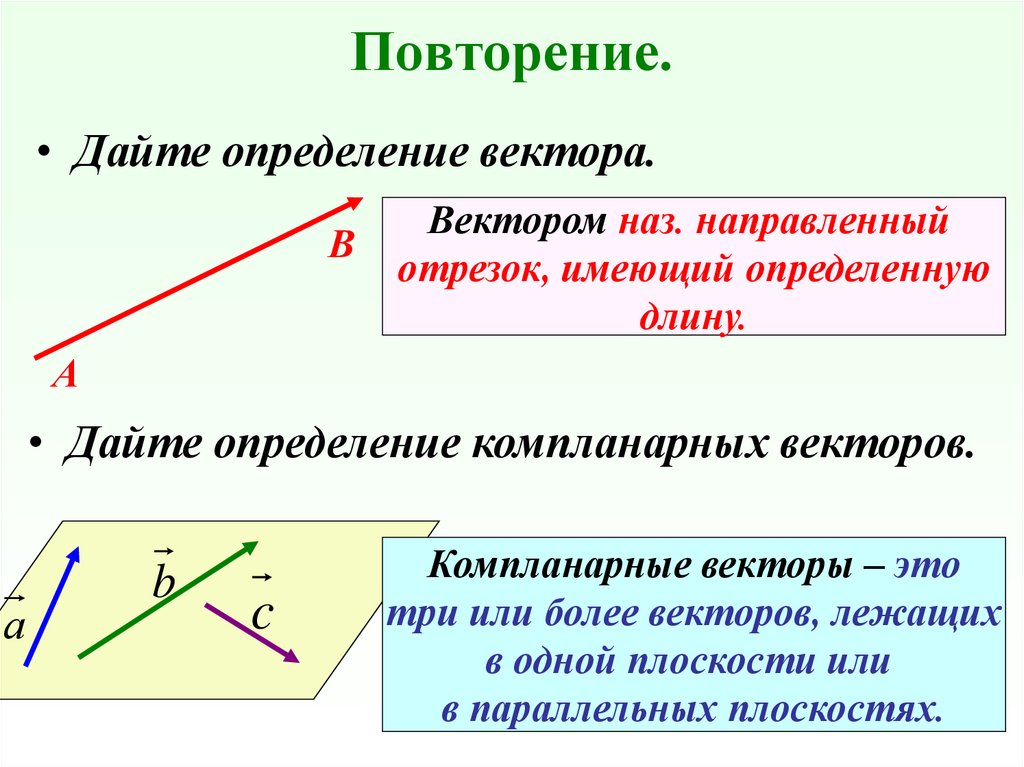
• Дайте определение вектора.В
Вектором наз. направленный
отрезок, имеющий определенную
длину.
А
• Дайте определение компланарных векторов.
а
b
α
c
Компланарные векторы – это
три или более векторов, лежащих
в одной плоскости или
в параллельных плоскостях.
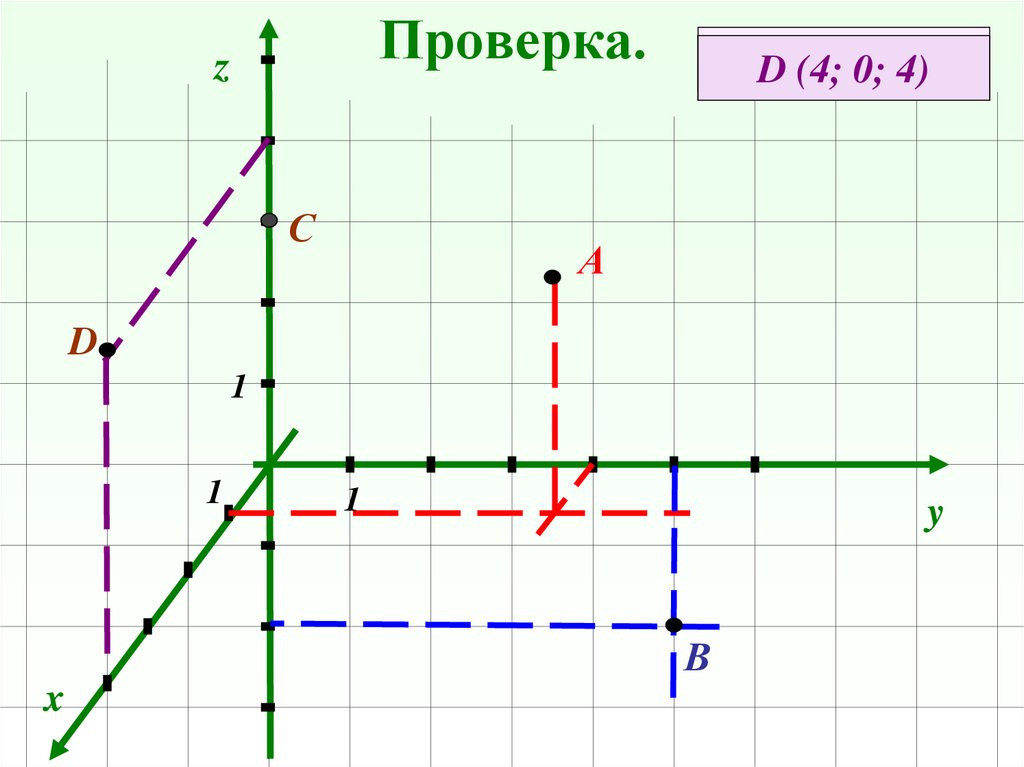
6. Выполнение задания с последующей проверкой.
Начертить прямоугольную трехмернуюсистему координат и отметить в ней
точки:
А (1; 4; 3); В (0; 5; -3); С (0; 0; 3) и D (4; 0; 4)
7. Проверка.
zС
А
(1;
4;
3)
В
D
С (0;
(0;
(4; 5;
0;
0; -3)
3)
4)
А
D
1
1
1
y
В
x
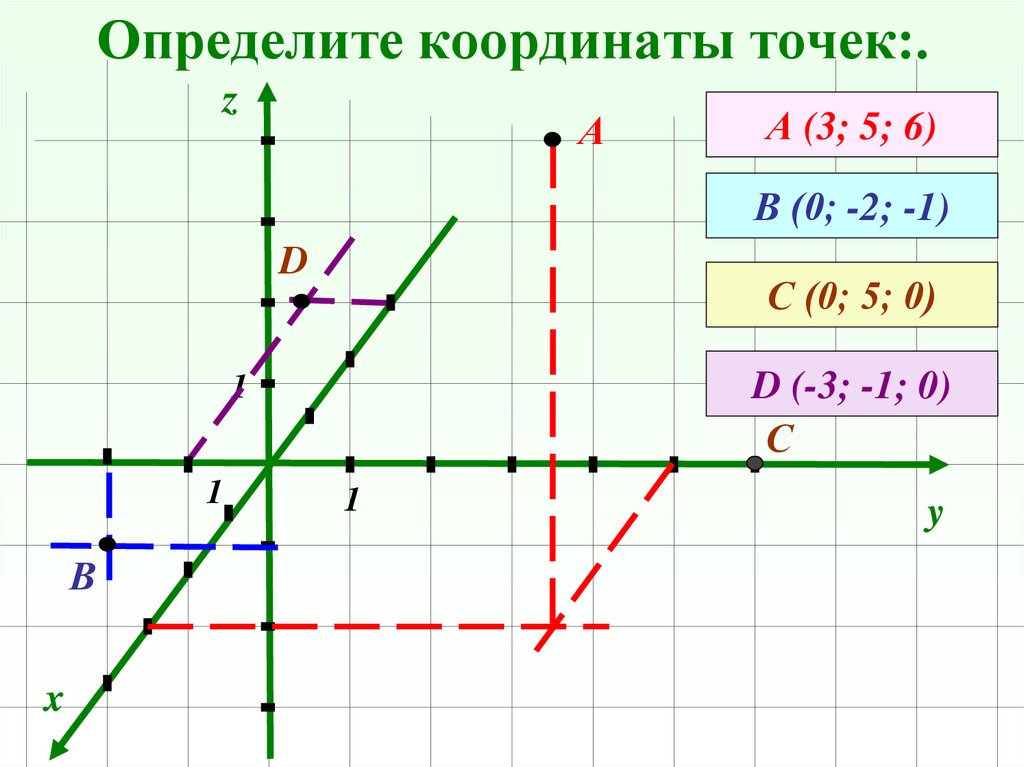
8. Определите координаты точек:.
zА
А (3; 5; 6)
В (0; -2; -1)
D
С (0; 5; 0)
D (-3; -1; 0)
С
1
1
В
x
1
y
9. Думаем… Отвечаем…
• Даны точкиА (2; 4; 5), В (3; а; b), C (0; 4; d) и D (5; n; m)
При каких значениях а, b, d, n и m эти точки
лежат:
1) В плоскости, параллельной плоскости Оху
а, п – любые; b = d = 5
2) В плоскости, параллельной плоскости Охz
a = п = 4; b, d, m - любые
3) На прямой параллельной оси Ох
a = п = 4; b = d = m = 5
?
?
?
10. Изучение нового материала.
za xi y j z k
1
k
i
1
x
О
a x; y; z
j
1
y
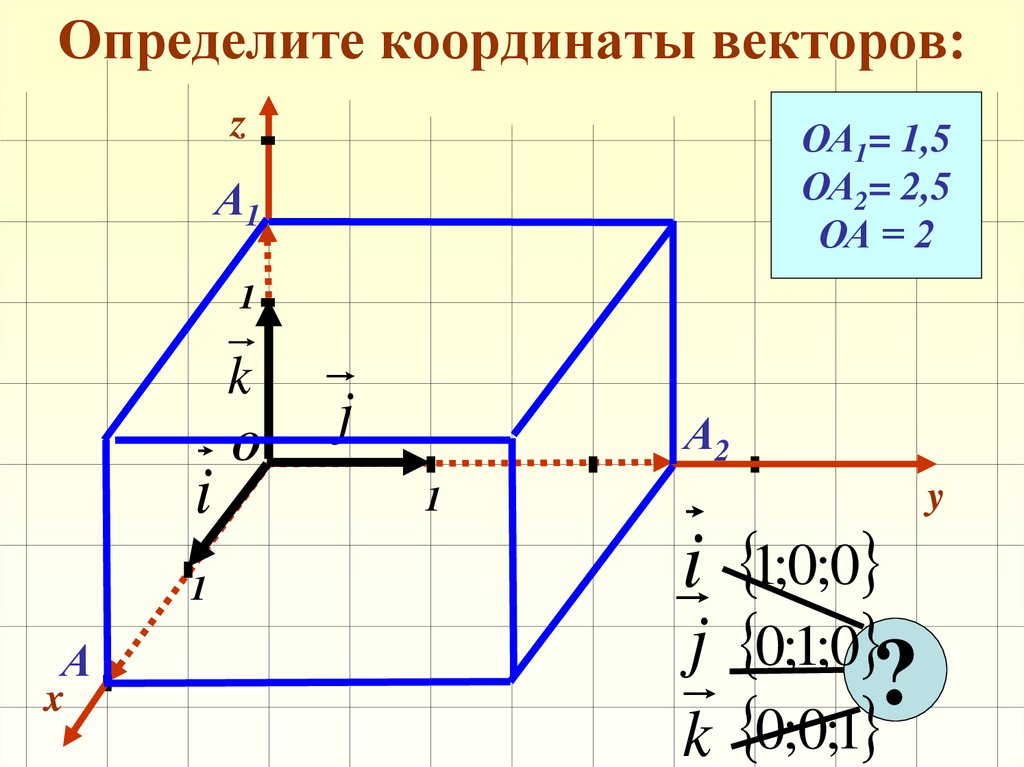
11. Определите координаты векторов:
zОА1= 1,5
ОА2= 2,5
ОА = 2
А1
1
k
i
1
А
x
О
j
А2
1
i 1;0;0
j 0;1;0
k
?
0;0;1
y
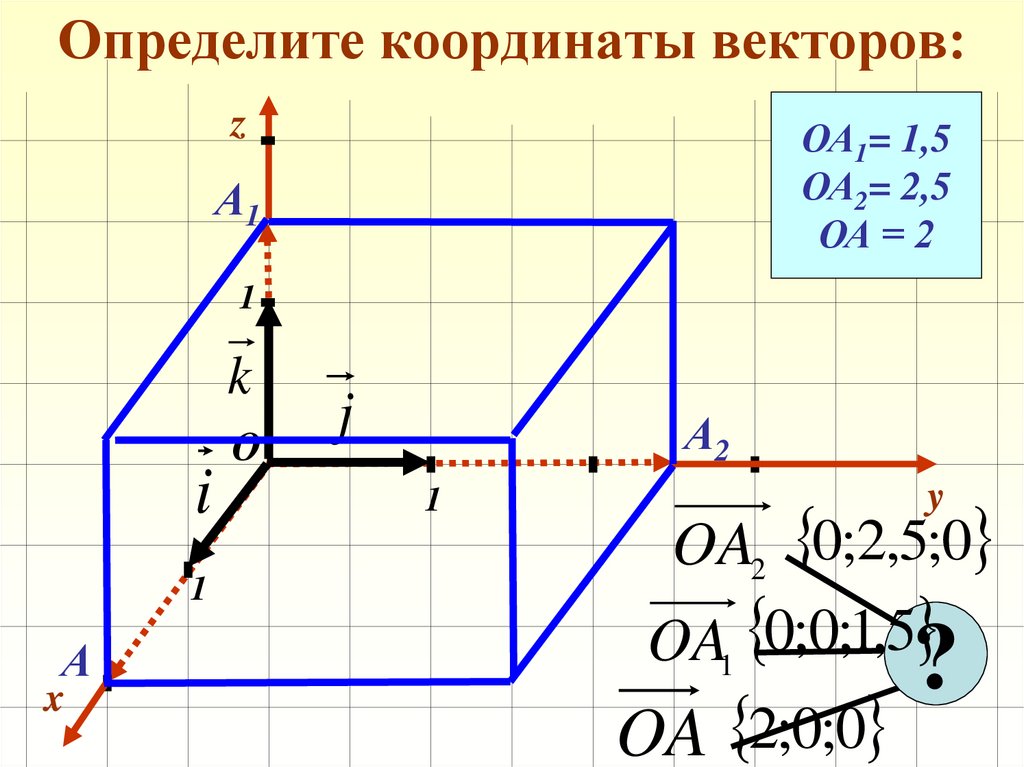
12. Определите координаты векторов:
zОА1= 1,5
ОА2= 2,5
ОА = 2
А1
1
k
i
1
А
x
О
j
А2
1
y
OA2 0;2,5;0
OA1 0;0;1,5
OA 2;0;0
?
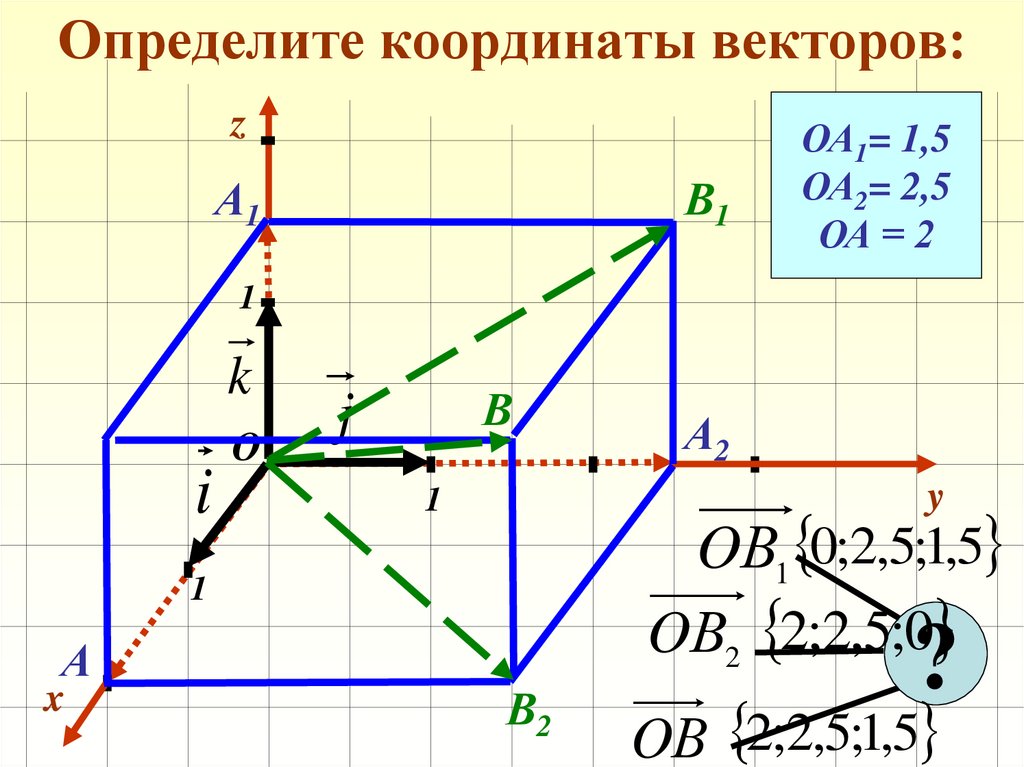
13. Определите координаты векторов:
zА1
В1
ОА1= 1,5
ОА2= 2,5
ОА = 2
1
k
i
О
В
j
y
1
OВ1 0;2,5;1,5
OВ2 2;2,5;0
1
А
x
А2
В2
?
OВ 2;2,5;1,5
14. Разложите все векторы по координатным векторам.
Проверяем:ОА1 0 i 0 j 1,5 k
ОА2 0 i 2,5 j 0 k
ОА 2 i 0 j 0 k
ОB1 0 i 2,5 j 1,5 k
ОB2 2 i 2,5 j 0 k
ОB 2 i 2,5 j 1,5 k
15. Правила действий над векторами с заданными координатами.
1. Равные векторы имеют равные координаты.Пусть
а х1 ; у1 ; z1
b х2 ; у2 ; z2
a х1 i; у1 j; z1 k
a b
b х i; у
2
2
j; z 2 k
, тогда
a b 0
a b х1 i y1 j z1 k x2 i y2 j z2 k
x1 x2 i y1 y2 j z1 z2 k 0 i 0 j 0 k 0
Следовательно
х1 = х2; у1 = у2; z1 = z2
16. Правила действий над векторами с заданными координатами.
2. Каждая координата суммы двух (и более) векторов равнасумме соответствующих координат этих векторов.
Дано:
а х1; у1; z1
b х2 ; у2 ; z2
с a b
Доказать: с х1 х2 ; у1 у2 ; z1 z2
a х1 i; у1 j; z1 k
b х i; у
2
2
j; z 2 k
a b х1 i y1 j z1 k x2 i y2 j z2 k
x1 x2 i y1 y2 j z1 z2 k с
Следовательно
с х1 х2 ; у1 у2 ; z1 z2
17. Правила действий над векторами с заданными координатами.
3. Каждая координата произведения вектора на числоравна произведению соответствующей координаты
на это число.
Дано: а х; у; z α – произв.число
Доказать: с х; у; z
a с
4. Каждая координата разности двух векторов равна
число равна разности соответствующих координат
на этих векторов.
Дано: а х1 ; у1 ; z1 b х2 ; у2 ; z2 с a b
Доказать: с х1 х2 ; у1 у2 ; z1 z2
Доказательства выполнить дома.
18. Домашнее задание:
Доказательства двух правилдействий над векторами.
№№ 403, 404, 407
Повторить определение средней линии
треугольника и теорему о средней линии
треугольника.
19. Выполнить задание устно:
• Даны векторы:а 3;5; 7
b 4; 1;3
c 0;1;8
d 3;0;0
• Найти вектор равный:
а) 2 а 2 а 6;10; 14 б ) 3 b
в) a b a b 7;4; 4
г) b с
e) 3d 2c
b с 4; 2; 5
д) а b d
3 b 12;3; 9
а b d 10;4; 4
3d 2c 9; 2; 8
20. Письменно:
№№ 403; 404;№ 407 – по вариантам.
I вариант – а, в, д.
II вариант – б, г, е













 Математика
Математика








