Пересечение поверхностей. Способ вспомогательных секущих плоскостей

1.

Пересечение поверхностей.
Способ вспомогательных секущих
плоскостей.

2.

Пересечение поверхностей
а)
б)
в)
г)
Геометрическое место точек,
принадлежащее одновременно двум поверхностям, называют
линией пересечения данных поверхностей
Возможные случаи:
Одна замкнутая линия
(врезание одной в другую)
Две многогранные поверхности
(ломаная линия)
Две замкнутые линии
(пересечение насквозь)
Кривая и гранная поверхности
(совокупность плоских кривых)
Для построения линии пересечения поверхностей необходимо найти ряд
точек, общих для заданных поверхностей, и соединить их плавной
линией

3.

Анализ заданных поверхностей
1. Линия пересечения 2-х поверхностей
в общем случае представляет собой
пространственную кривую
2. Если заданы поверхности второго
порядка, то при их пересечении
получается пространственная кривая
четвертого порядка
3. Часть искомой линии
пересечения получается
видимой в пересечении
видимых частей
поверхностей

4.

Анализ заданных поверхностей
4. Если одна из заданных поверхностей
является проецирующей (цилиндр,
призма),то одна из проекций искомой
линии пересечения совпадает со следом
этой поверхности

5.

Анализ заданных поверхностей
5.
Если у заданных поверхностей 2 порядка есть
общая плоскость симметрии , которая проходит
через их оси вращения, то:
Линия пересечения будет симметрична относительно
плоскости
Наивысшая 1 и низшая 2 точки линии пересечения
всегда располагаются в плоскости
Если плоскость параллельна плоскости проекций, то
на ней линия пересечения будет кривой второго
порядка, ее видимая и невидимая части накладываются
1
1
2
2
2
2
2
1
1
1
1
2
2
1
2
1
1

6.

Алгоритм решения задачи
B
Г
a
А
b
1. Поверхности рассекают
вспомогательной секущей
плоскостью Г
2. Находят линию
пересечения
вспомогательной плоскости
с каждой из поверхностей
Г а ; Г b
3. На полученных линиях
пересечения определяют
общие точки, принадлежащие
заданным поверхностям
a b A,B
4. Выбирают следующую секущую плоскость и повторяют
алгоритм
5. Полученные точки соединяют с учетом видимости
искомой линии пересечения

7.

Методические указания
• Вспомогательные плоскости следует
выбирать так, чтобы в сечении получались
простые линии
• Сначала определяют опорные точки:
экстремальные точки;
точки перемены видимости, лежащие на
очерках поверхностей;
особые точки кривых пересечения (концы
осей эллипса, вершины гиперболы или
параболы, вершины ломанной)
• Уточняют линию пересечения с помощью
промежуточных точек

8.

4.ПО
Ф1
Пересекающиеся поверхности (сфера и конус) имеют общую плоскость
симметрии Ф(Ф1), являющейся фронтальной плоскостью уровня.
Следовательно, фронтальные очерки поверхностей, лежащие в
плоскости Ф, пересекаются.

9.

4.ПО
12
22
(21)
11
Ф1
На П2 находим проекции высшей (12) и низшей (22) точек искомой линии,
как точек пересечения фронтальных очерков поверхностей.
Горизонтальные проекции точек (11 и 21) будут располагаться на следе
плоскости Ф1.

10.

4.ПО
12
Г2
32 (42)
22
41
(21)
11
Ф1
31
Точки изменения видимости линии на П1, лежащие на экваторе сферы,
находим с помощью плоскости Г(Г2). На П1 это будут точки пересечения
экватора сферы с соответствующей параллелью конуса - 31 и 41. На П2
проекции точек (32 и 42) располагаем на следе плоскости (Г2).

11.

4.ПО
12
Г2
Г2
32 (42)
Г2
22
41
(21)
11
Ф1
31
Промежуточные точки, уточняющие форму линии пересечения, находим с
помощью вспомогательных горизонтальных плоскостей уровня Г и Г
На П1 это будут точки пересечения соответствующих параллелей сферы
и конуса. Точки можно оставить без обозначения.

12.

4.ПО
12
Г2
Г2
32 (42)
Г2
22
41
(21)
11
Ф1
31
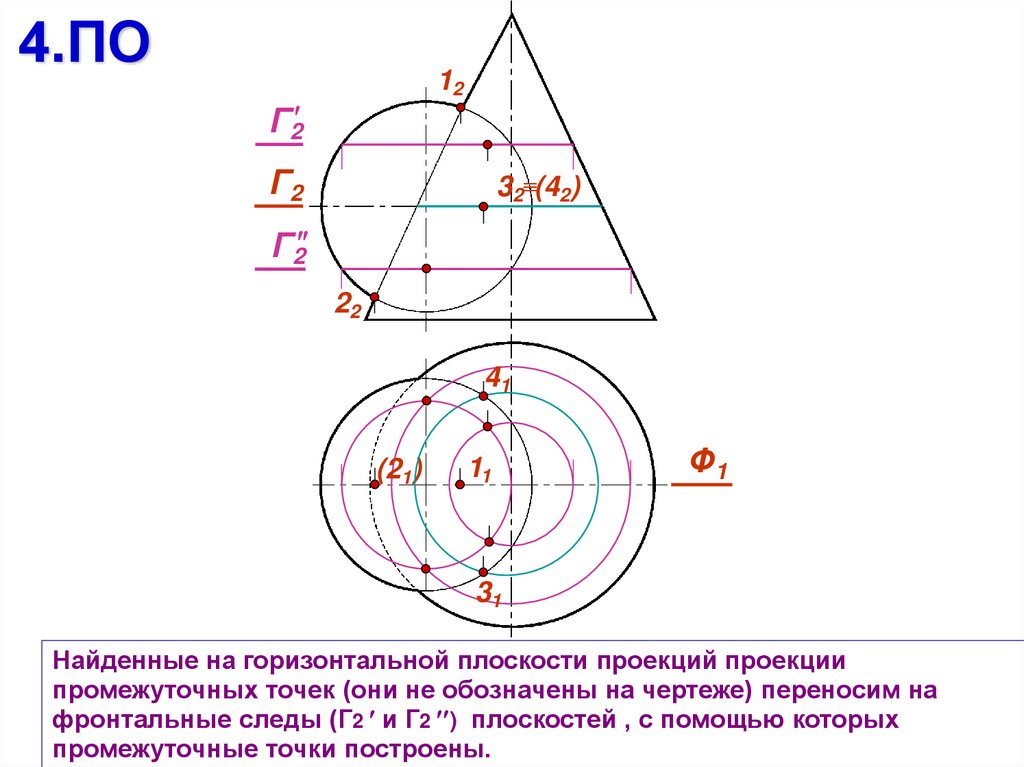
Найденные на горизонтальной плоскости проекций проекции
промежуточных точек (они не обозначены на чертеже) переносим на
фронтальные следы (Г2 и Г2 ) плоскостей , с помощью которых
промежуточные точки построены.

13.

4.ПО
12
Г2
Г2
32 (42)
Г2
22
41
(21)
11
Ф1
31
При объединении в линию всех построенных проекций точек на П2
следует учитывать, что вся линия пересечения разделяется плоскостью
Ф на две симметричные ветви, которые совпадут на фронтальной
плоскости проекций.

14.

4.ПО
12
Г2
Г2
32 (42)
Г2
22
41
(21)
11
Ф1
31
При соединении проекций точек на горизонтальной плоскости проекций
выявляют видимый и невидимый участки линии пересечения. Эти
участки разделяются проекциями точек перемены видимости - 31 и 41,
лежащими на экваторе сферы.

15.

4.ПО
12
Г2
Г2
32 (42)
Г2
22
41
(21)
11
Ф1
31
На этапе обводки очерков поверхностей следует обвести толстой
сплошной линией только очерки, не участвующие в пересечении

16.

4.ПО
12
Г2
Г2
32 (42)
Г2
22
41
(21)
11
Ф1
31
Видимая часть поверхности сферы, ограниченная линией пересечения,
затушевана, что повышает наглядность изображения.

17.

4.ПО
12
Г2
Г2
32 (42)
Г2
22
41
(21)
11
Ф1
31
Заканчиваем оформление изображения, затушевав видимую часть
поверхности конуса.

18.

5.ПО
Заданы две пересекающиеся поверхности (полусфера и призма, находящаяся в горизонтально проецирующем положении). Все три грани призмы участвуют в пересечении. Значит, линия пересечения состоит из трех
участков, представляющих собой плоские кривые второго порядка.

19.

5.ПО
(32
)
22
Ф1
31
(12
)
11
21
Фиксируем на П1 проекции точек пересечения ребер призмы с поверхностью сферы (11, 21 и 31). На П2 проекции 12 и 22 находим на экваторе
сферы, а 32 - на параллели, полученной с помощью плоскости Ф(Ф1).
Часть параллели между 32 и 42 будет первым участком искомой линии.

20.

5.ПО
42
52
(32
)
22
Ф1
(12
)
31
11
41
51
Ф1
21
На П1 проекции 41 и 51 фиксируем как точки пересечения меридиана
сферы, лежащего в плоскости Ф (Ф1 ), с гранями призмы. Фронтальные
проекций указанных точек (42 и 52) располагаем на меридиане сферы. Это
будут точки, меняющие видимость линии пересечения на П2.

21.

5.ПО
42 62
7252
(32
)
22
Ф1
31
Ф1
41
(12
)
11
51
61
71
Ф1
Ф1
21
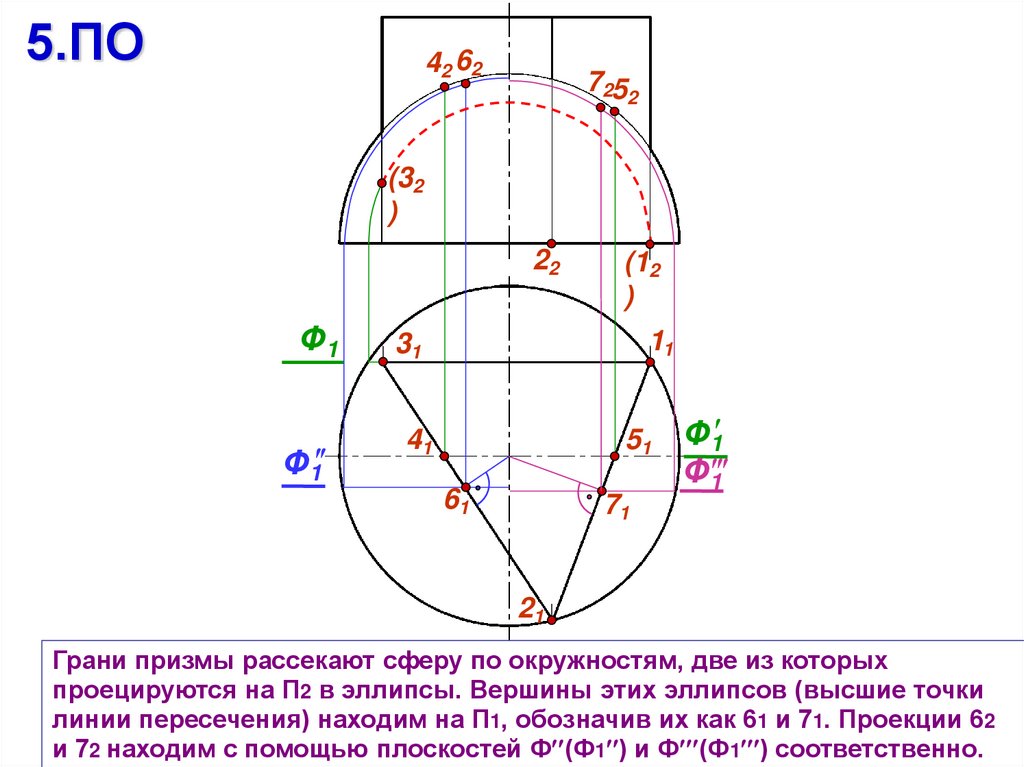
Грани призмы рассекают сферу по окружностям, две из которых
проецируются на П2 в эллипсы. Вершины этих эллипсов (высшие точки
линии пересечения) находим на П1, обозначив их как 61 и 71. Проекции 62
и 72 находим с помощью плоскостей Ф (Ф1 ) и Ф (Ф1 ) соответственно.

22.

5.ПО
42 62
7252
(32
)
22
Ф1
31
Ф1
41
(12
)
11
51
61
71
Ф1
Ф1
Ф1IV
21
Промежуточные точки линии пересечения, уточняющие форму эллипсов
и выбранные произвольно на горизонтальном очерке призмы, строим на
П2 с помощью секущей плоскости ФIV(Ф1IV) по аналогии с другими
точками. Промежуточные точки не обозначены.

23.

5.ПО
42 62
7252
(32
)
22
Ф1
31
Ф1
41
(12
)
11
51
61
71
Ф1
Ф1
Ф1IV
21
На П2 объединяем все построенные точки в участки - эллипсы линии пересечения, а на П1 вся линия совпадает с очерком проецирующей призмы. При обводке эллипсов на П2 следует учитывать, что проекции точек
(42 и 52), лежащих на меридиане сферы, изменяют видимость эллипсов.

24.

5.ПО
42 62
7252
(32
)
22
Ф1
31
Ф1
41
(12
)
11
51
61
71
Ф1
Ф1
Ф1IV
21
На П2 обводим фронтальные очерки сферы и призмы, выявляя их
видимые и невидимые участки.

25.

5.ПО
42 62
7252
(32
)
22
Ф1
31
Ф1
41
(12
)
11
51
61
71
Ф1
Ф1
Ф1IV
21
Тушевка повышает наглядность изображения.
На П2 видимая часть поверхности сферы ограничивается линией
пересечения и видимой частью очерка сферы.

26.

5.ПО
42 62
7252
(32
)
22
Ф1
31
Ф1
41
(12
)
11
51
61
71
Ф1
Ф1
Ф1IV
21
На П2 заканчиваем оформление изображения, затушевав видимую часть
поверхности призмы.

27.

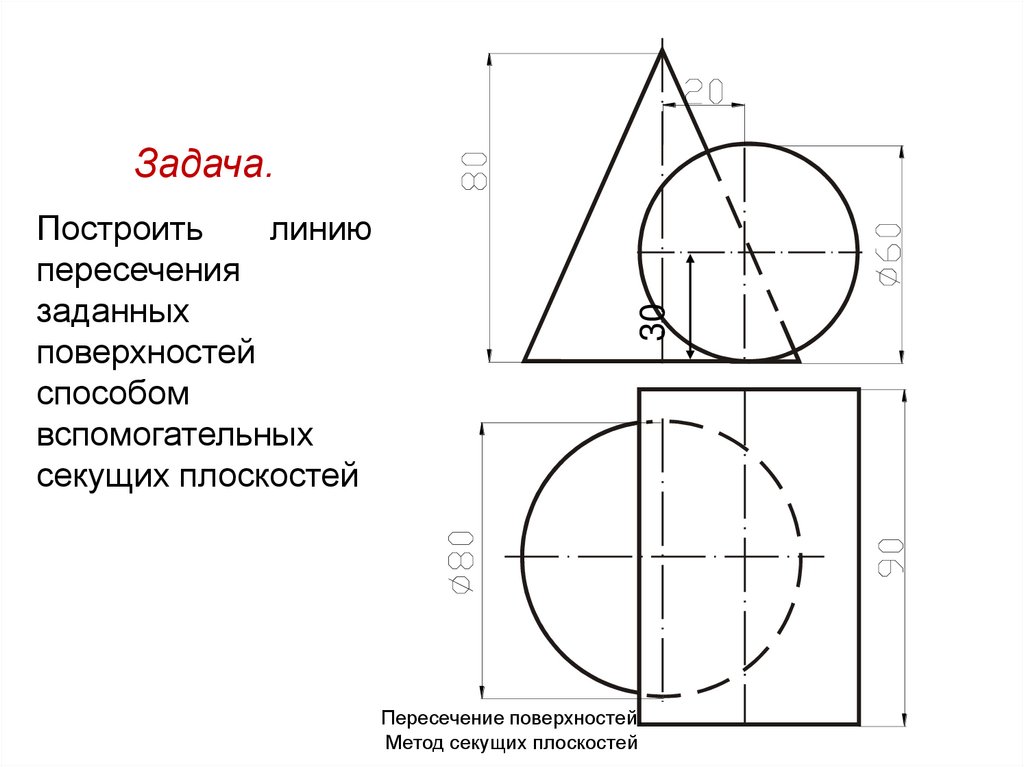
Построить
линию
пересечения
заданных
поверхностей
способом
вспомогательных
секущих плоскостей
30
Задача.
Пересечение поверхностей.
Метод секущих плоскостей
27

28.

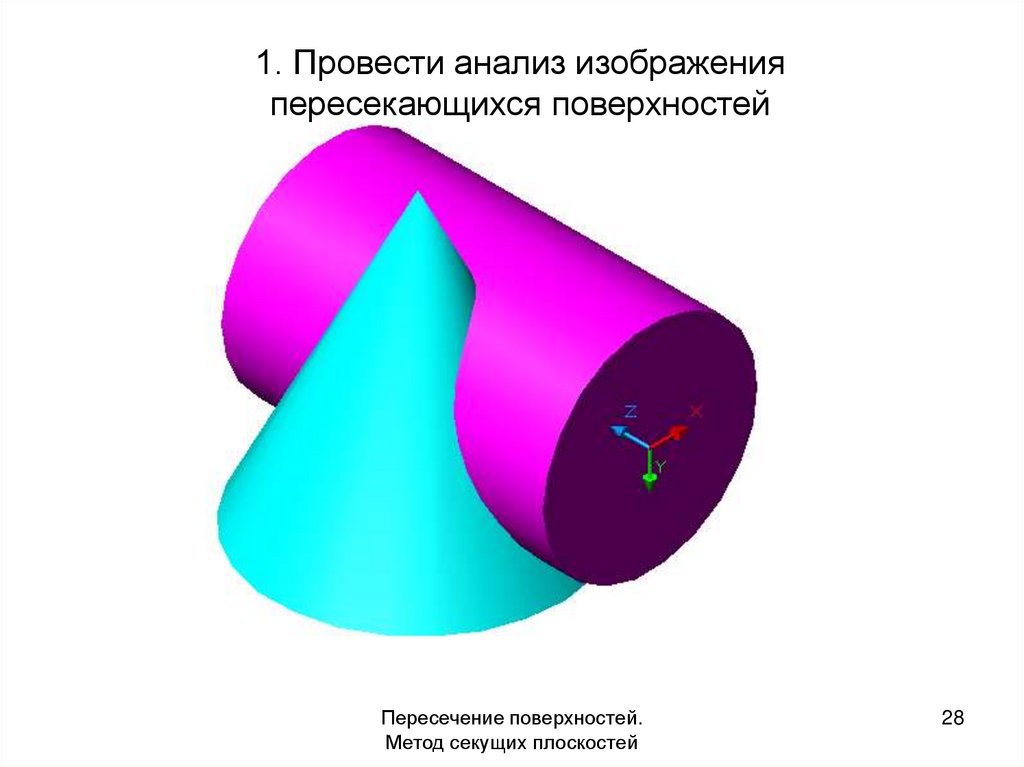
1. Провести анализ изображения
пересекающихся поверхностей
Пересечение поверхностей.
Метод секущих плоскостей
28

29.

Цилиндр является
фронтально
проецирующей
поверхностью, так как
все его образующие
фронтально
проецирующие
прямые
Линия пересечения
заданных
поверхностей на
фронтальной
плоскости совпадает
с очерком цилиндра
Пересечение поверхностей.
Метод секущих плоскостей
29

30.

12
Характерные точки
22
11
- точки пересечения
очерков точки 1 и 2
на горизонтальной
плоскости находятся
на оси конуса
21
Пересечение поверхностей.
Метод секущих плоскостей
30

31.

12
Характерные точки
- низшие точки
очерка цилиндра
12
9 и 10 лежат на
основании конуса
12
22
11
22
11
21
22
21
92Ξ102
91
12
22
11
21
11
21
Пересечение поверхностей.
10
1
Метод секущих плоскостей
31

32.

12
π2
52Ξ62
12
22
11
21
22
92Ξ102
91
12
22
11
21
11
• Характерные
точки
- крайние левые
точки очерка
цилиндра (точки
5 и 6), находятся
с помощью
вспомогательной
плоскости π2
21
Пересечение поверхностей.
10
1
Метод секущих плоскостей
32

33.

R5
В плоскости π2
фигура сечения конуса –
это окружность R5,
а фигура сечения
цилиндра по его оси –
прямоугольник
Пересечение поверхностей.
Метод секущих плоскостей
33

34.

R3
b п2
Промежуточные точки
- 3 и 4 находятся с
помощью
дополнительной
секущей плоскости bп2,
которая рассекает конус
по окружности R3, а
цилиндр по
прямоугольнику
На пересечении этих
фигур находятся точки
взаимного пересечения
поверхностей
Пересечение поверхностей.
Метод секущих плоскостей
34

35.

Промежуточные
точки
R7
72 Ξ 82
81
71
п2
- 7 и 8 строятся
аналогично
предыдущим.
Проводят
вспомогательную
плоскость п2
Плоскость рассекает конус
по окружности R7, а
цилиндр по прямоугольнику
Пересечение поверхностей.
Метод секущих плоскостей
35

36.

Соединяют полученные
точки в последовательности,
как на проецирующей
поверхности конуса:
1,3,5,7,9,2,10,8,6,4,1
Обводят
изображение с
учетом видимости
Пересечение поверхностей.
Метод секущих плоскостей
36

37.

Выводы по теме
• Геометрические фигуры сечений
поверхностей строят с помощью метода
вспомогательных секущих плоскостей
• Секущие плоскости – посредники
должны занимать частное положение
• Взаимное пересечение поверхностей –
линии принадлежащие двум
поверхностям одновременно
Пересечение поверхностей.
Метод секущих плоскостей
37

38.

Рекомендованная литература
• Бударин О. С. Начертательная геометрия. Краткий
курс: учеб. пособие для студентов вузов,
обучающихся по направлениям в обл. техники и
технологий / О. С. Бударин. - 2-е изд., испр. - СанктПетербург ; Москва ; Краснодар: Лань, 2009. - 368 с.
• Королев Ю. И. Начертательная геометрия: учеб. для
вузов инженер.-техн. специальностей / Ю. И.
Королев. - 2-е изд. - Москва ; Санкт-Петербург ;
Нижний Новгород [и др.]: Питер, 2010. - 256 с.
• Чекмарев А. А. Начертательная геометрия и
черчение: учеб. для студентов вузов, обучающихся
по техн. специальностям / А. А. Чекмарев. - 3-е изд.,
перераб. и доп. - Москва: Юрайт, 2011. - 471 с.
Пересечение поверхностей. Метод секущих
плоскостей
38