Взаимное пересечение кривых поверхностей. Лекция 12

1.

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ
ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
"САМАРСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ
УНИВЕРСИТЕТ ИМЕНИ АКАДЕМИКА С.П. КОРОЛЕВА»
(САМАРСКИЙ УНИВЕРСИТЕТ)
Лекция 12
Взаимное
пересечение
кривых
поверхностей

2.

Взаимное пересечение
поверхностей
Вид линии пересечения зависит от
сочетаний пересекающихся
поверхностей

3.

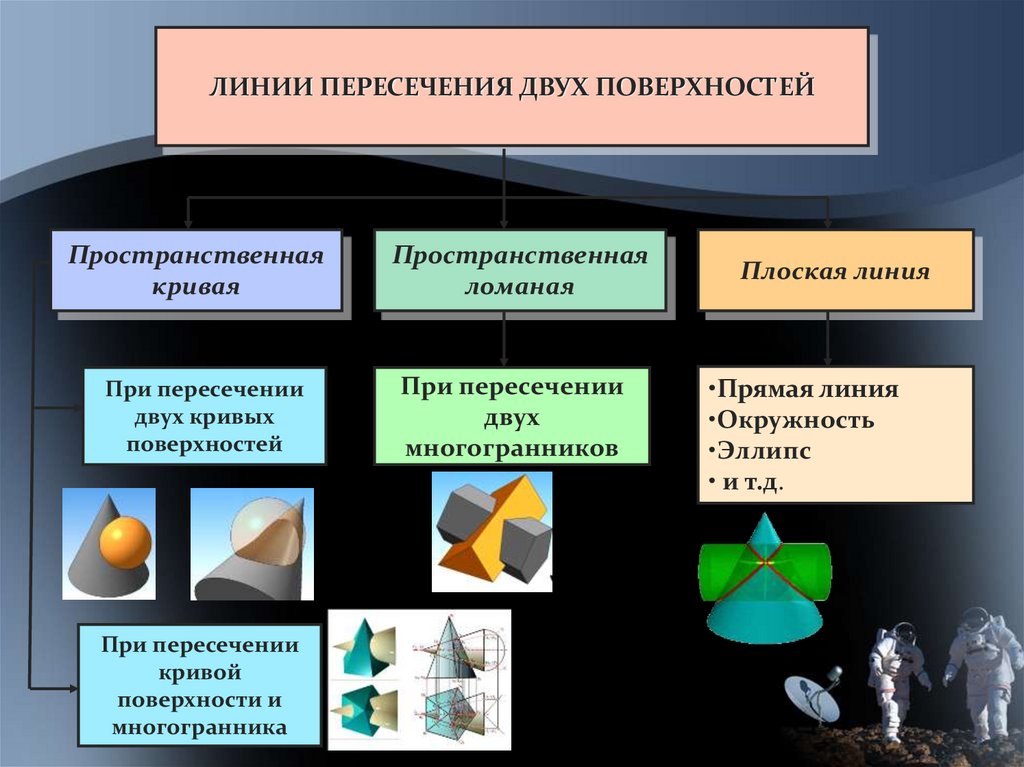
ЛИНИИ ПЕРЕСЕЧЕНИЯ ДВУХ ПОВЕРХНОСТЕЙ
Пространственная
кривая
При пересечении
двух кривых
поверхностей
При пересечении
кривой
поверхности и
многогранника
Пространственная
ломаная
При пересечении
двух
многогранников
Плоская линия
•Прямая линия
•Окружность
•Эллипс
• и т.д.

4.

ПЕРЕСЕЧЕНИЕ МОЖЕТ БЫТЬ
ПОЛНЫМ и НЕПОЛНЫМ (ВРЕЗАНИЕ)
В ПЕРВОМ СЛУЧАЕ - ДВА ЗАМКНУТЫХ КОНТУРА
ЛИНИИ ПЕРЕСЕЧЕНИЯ
ПРИ ВРЕЗАНИИ - ОДИН ЗАМКНУТЫЙ КОНТУР

5.

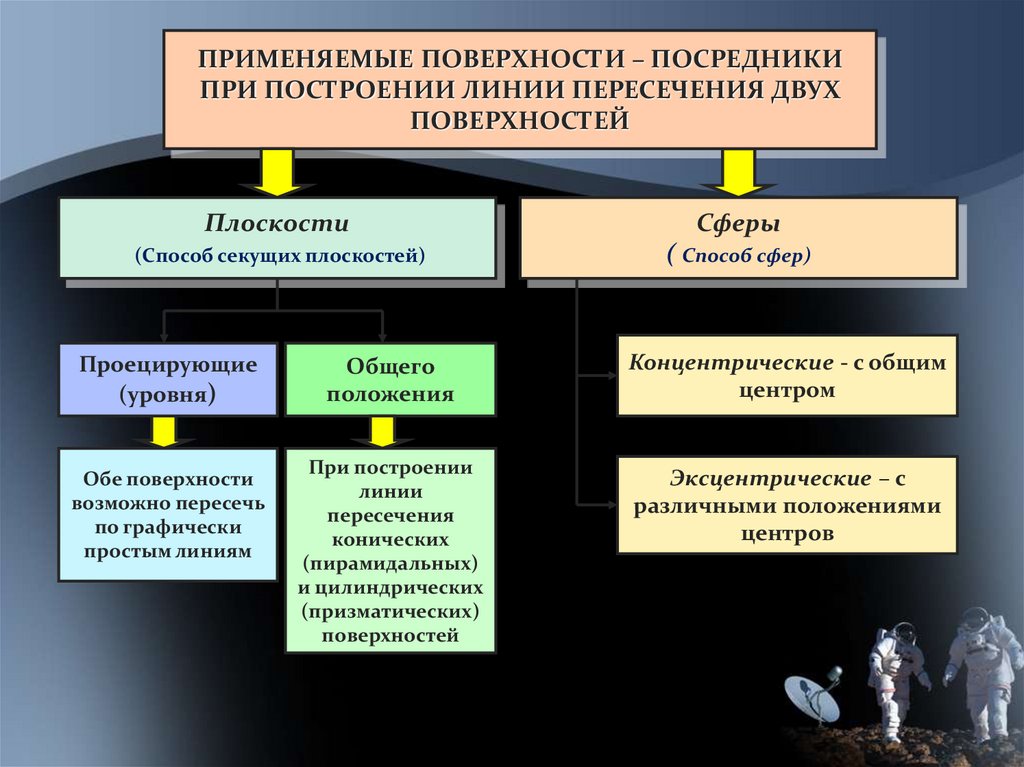
ПРИМЕНЯЕМЫЕ ПОВЕРХНОСТИ – ПОСРЕДНИКИ
ПРИ ПОСТРОЕНИИ ЛИНИИ ПЕРЕСЕЧЕНИЯ ДВУХ
ПОВЕРХНОСТЕЙ
Плоскости
Сферы
(Способ секущих плоскостей)
( Способ сфер)
Проецирующие
(уровня)
Обе поверхности
возможно пересечь
по графически
простым линиям
Общего
положения
Концентрические - с общим
центром
При построении
линии
пересечения
конических
(пирамидальных)
и цилиндрических
(призматических)
поверхностей
Эксцентрические – с
различными положениями
центров

6.

Взаимное пересечение
поверхностей
Метод вспомогательных секущих
плоскостей

7.

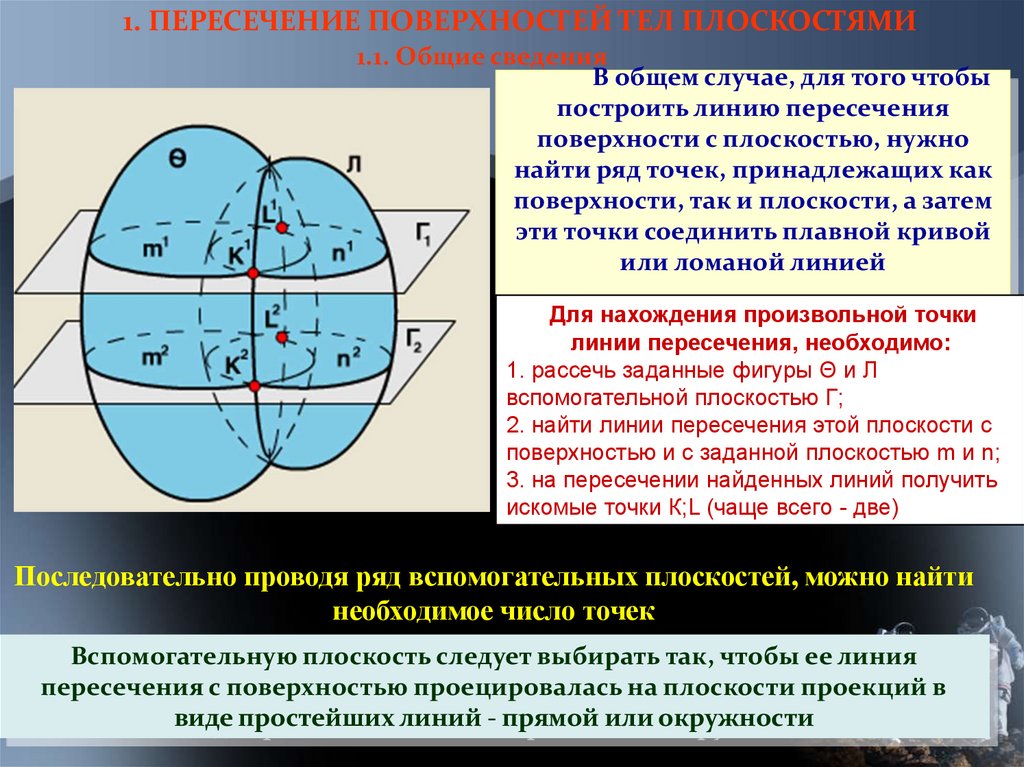
1. ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ ТЕЛ ПЛОСКОСТЯМИ
1.1. Общие сведения
В общем случае, для того чтобы
построить линию пересечения
поверхности с плоскостью, нужно
найти ряд точек, принадлежащих как
поверхности, так и плоскости, а затем
эти точки соединить плавной кривой
или ломаной линией
Для нахождения произвольной точки
линии пересечения, необходимо:
1. рассечь заданные фигуры Θ и Л
вспомогательной плоскостью Г;
2. найти линии пересечения этой плоскости с
поверхностью и с заданной плоскостью m и n;
3. на пересечении найденных линий получить
искомые точки К;L (чаще всего - две)
Последовательно проводя ряд вспомогательных плоскостей, можно найти
необходимое число точек
Вспомогательную плоскость следует выбирать так, чтобы ее линия
пересечения с поверхностью проецировалась на плоскости проекций в
виде простейших линий - прямой или окружности

8.

При построении линии пересечения находят прежде всего ее характерные
(опорные) точки, а затем, по мере необходимости, промежуточные точки.
Характерные точки определяют характер линии и ее видимость.
ХАРАКТЕРНЫЕ (ОПОРНЫЕ) ТОЧКИ
1
Экстремальные точки (высшая и низшая, крайняя
левая и крайняя правая, ближняя и дальняя)
2
Точки, лежащие на проекциях очерка поверхности
3
Точки, лежащие на проекциях осей поверхности
Среди характерных точек выделяются очевидные точки, которые для
своего нахождения не требуют дополнительных построений, а
определяются при помощи линий проекционной связи. В некоторых
случаях одна и та же точка может выполнять несколько функций.
Промежуточные точки выделяются на заданной линии для более
точного графического построения искомой проекции линии.

9.

2. ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ
2.1. Общие сведения
Для того чтобы построить линию
пересечения двух поверхностей, нужно
найти ряд общих точек, принадлежащих
им, а затем соединить эти точки в
определенной последовательности.
Линия пересечения не должна выходить за
очерки наложения двух поверхностей
Построение линии пересечения поверхностей в общем
случае осуществляется при помощи вспомогательных
секущих поверхностей - посредников
Вспомогательную поверхность следует выбирать так, чтобы
ее линия пересечения с каждой поверхностью
проецировалась на плоскости проекций в виде графически
простых линий − прямой или окружности

10.

Алгоритм решения задач
1. Анализ поверхностей. Определить наличие
проецирующей поверхности. В этом случае на
одной из плоскостей проекций уже имеется
одна проекция линии пересечения.
2. Нахождение характерных точек.
3. Проведение вспомогательной секущей
плоскости, которая выбирается из условия
получения в сечении простых геометрических
фигур
–
окружностей,
треугольников,
прямоугольников.

11.

4. Построение двух линий пересечения
обеих поверхностей вспомогательной
секущей плоскостью.
5. Определение точек пересечения двух
построенных линий.
6. Повторение пунктов 3, 4, 5 – n раз.
7. Соединение полученных точек
пересечения линией.
8. Определение видимости линий
пересечения и линий заданных
поверхностей.
11

12.

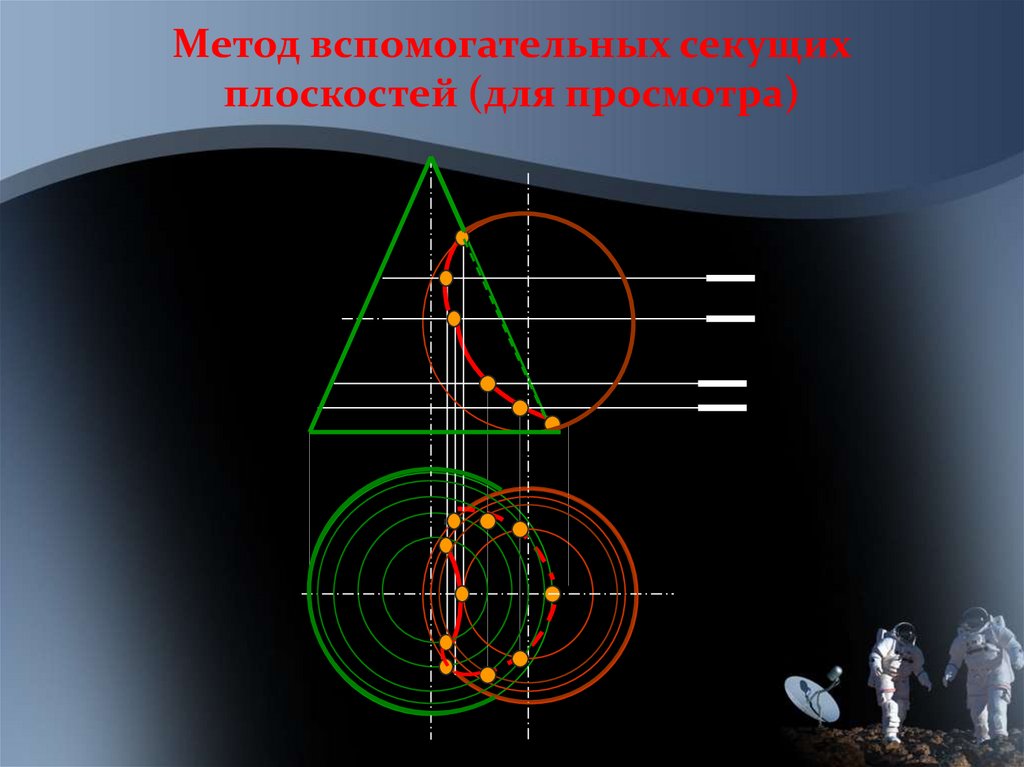
Метод вспомогательных секущих
плоскостей (для просмотра)

13.

ПРИМЕР: Построить линию
пересечения
сферы с конусом вращения
Для построения линии
пересечения заданных
поверхностей удобно в качестве
вспомогательных поверхностей
использовать ряд горизонтальных
плоскостей, перпендикулярных
оси конуса, которые пересекают
сферу и конус по окружностям. На
пересечении этих окружностей
находят точки искомой линии
пересечения
Так как пересекаются две
поверхности второго порядка,
линией пересечения будет
пространственная кривая
четвертого порядка

14.

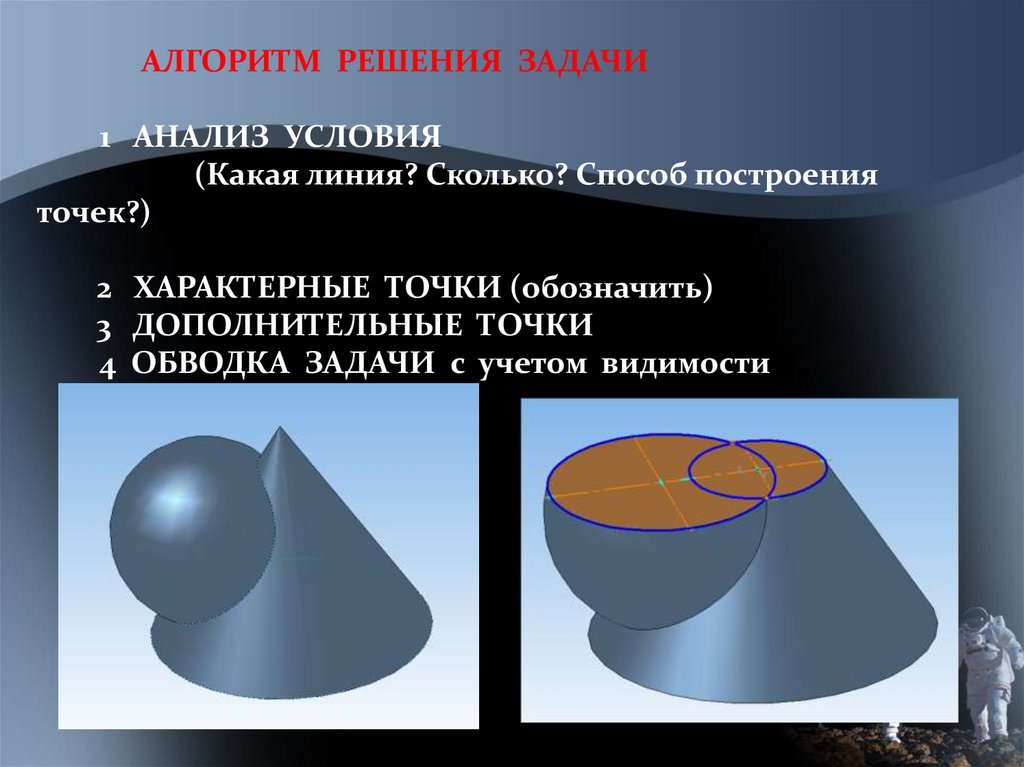
АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ
1 АНАЛИЗ УСЛОВИЯ
(Какая линия? Сколько? Способ построения
точек?)
2 ХАРАКТЕРНЫЕ ТОЧКИ (обозначить)
3 ДОПОЛНИТЕЛЬНЫЕ ТОЧКИ
4 ОБВОДКА ЗАДАЧИ с учетом видимости

15.

16.

ℓ
m2
m
ℓ2
Ф
ℓ1
m1
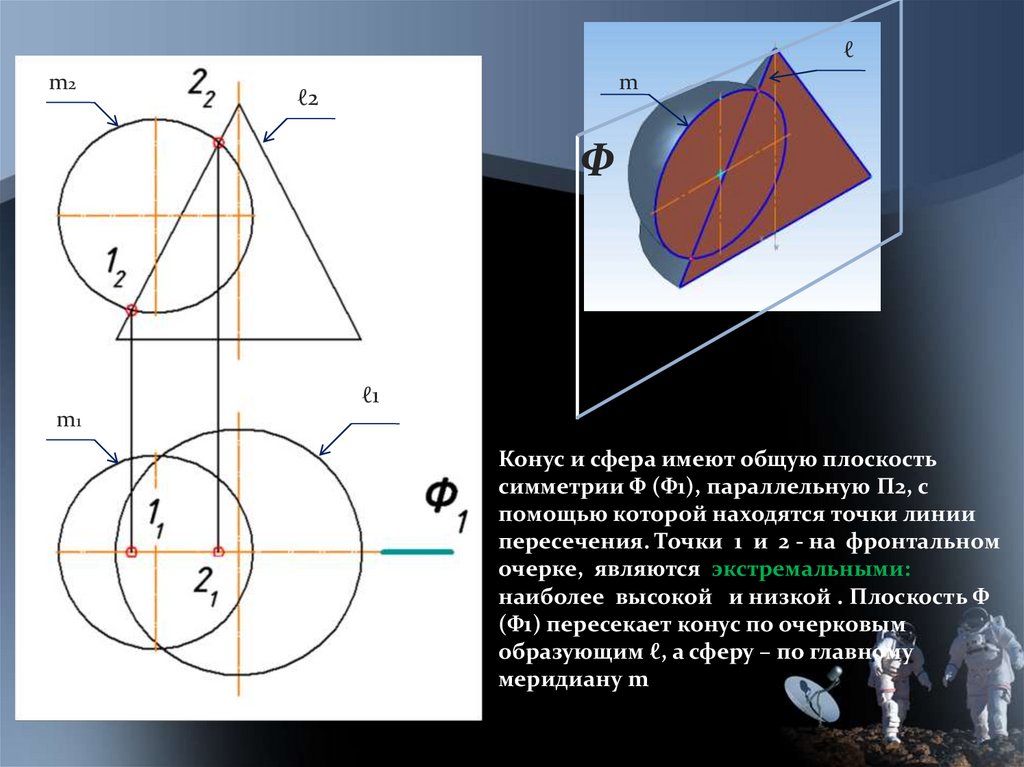
Конус и сфера имеют общую плоскость
симметрии Ф (Ф1), параллельную П2, с
помощью которой находятся точки линии
пересечения. Точки 1 и 2 - на фронтальном
очерке, являются экстремальными:
наиболее высокой и низкой . Плоскость Ф
(Ф1) пересекает конус по очерковым
образующим ℓ, а сферу – по главному
меридиану m

17.

Обе поверхности
содержат семейство
параллелей,
параллельных
горизонтальной
плоскости проекций,
поэтому остальные
точки линии сечения
необходимо находить с
помощью
горизонтальных
плоскостей уровня

18.

ЭКВАТОР
n2
Г2
r
n1
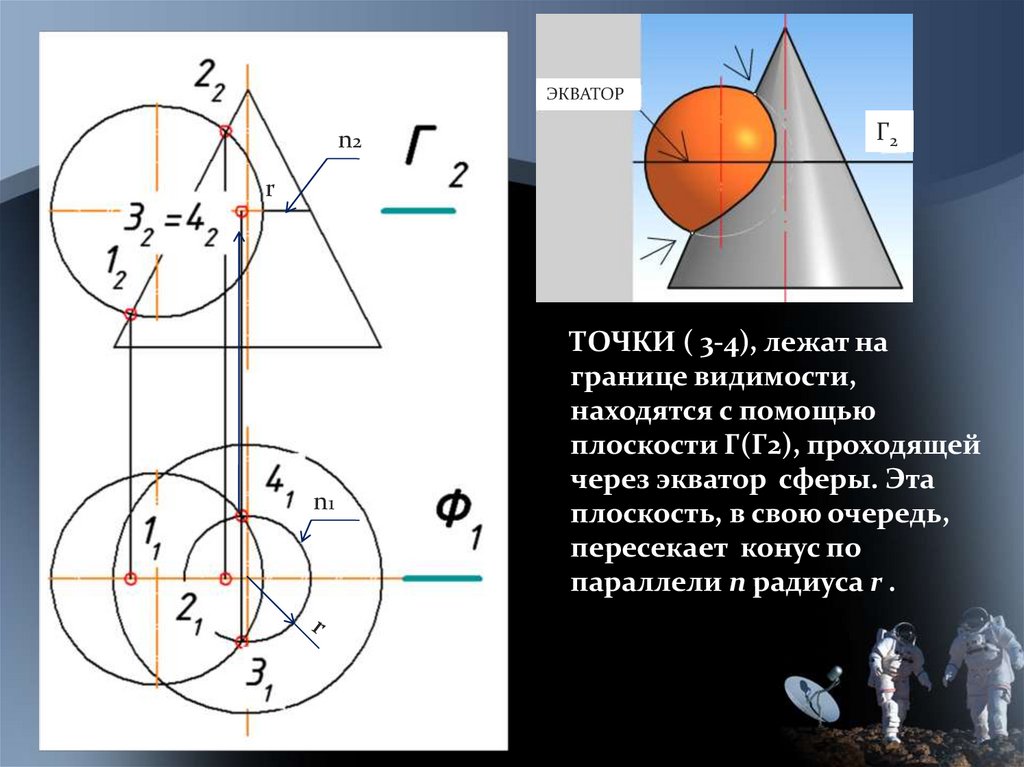
ТОЧКИ ( 3-4), лежат на
границе видимости,
находятся с помощью
плоскости Г(Г2), проходящей
через экватор сферы. Эта
плоскость, в свою очередь,
пересекает конус по
параллели n радиуса r .

19.

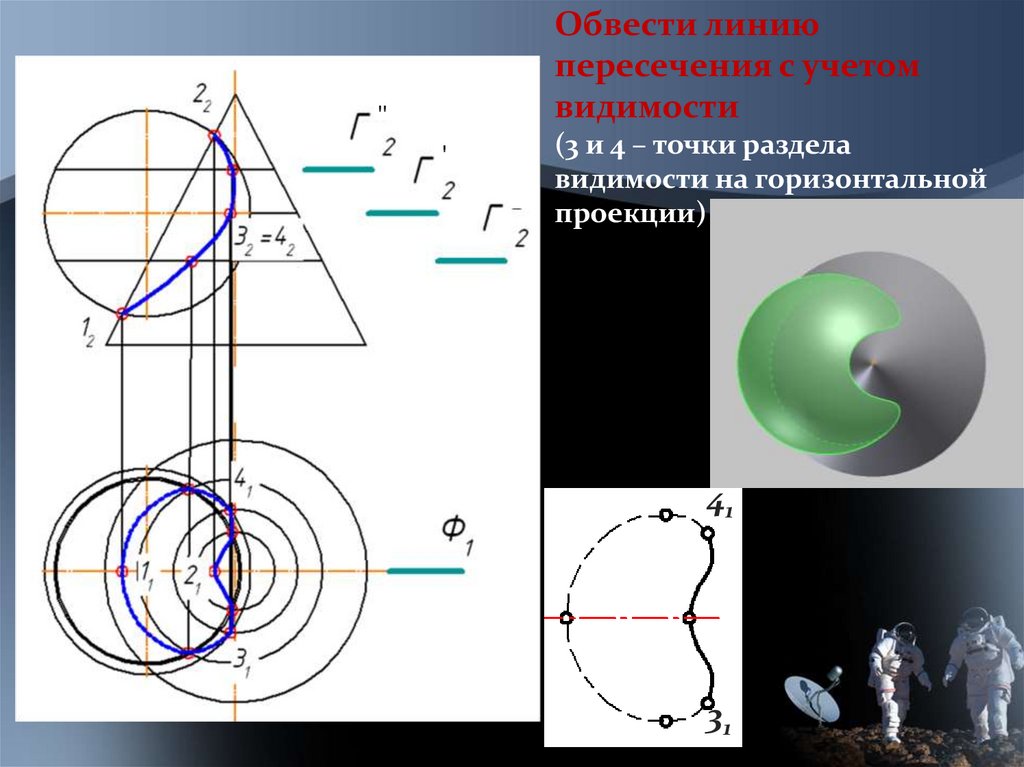
Обвести линию
пересечения с учетом
видимости
Г
ʹʹГ
ʹ
(3 и 4 – точки раздела
видимости на горизонтальной
проекции)
41
31

20.

ʹʹ
ʹ
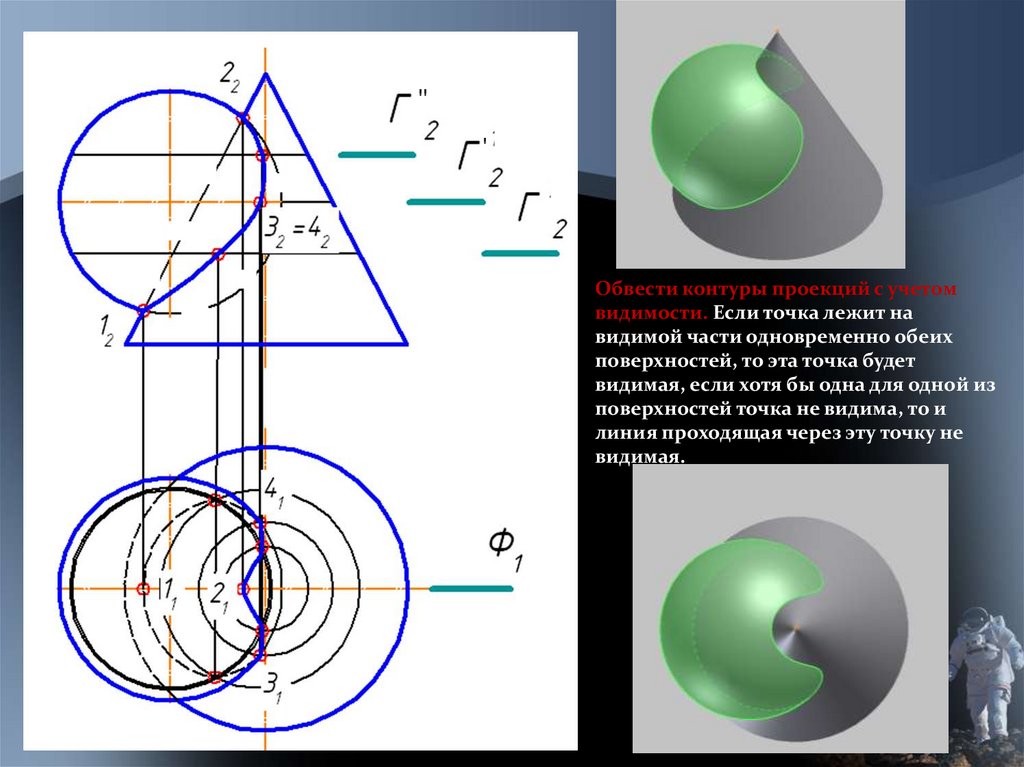
Обвести контуры проекций с учетом
видимости. Если точка лежит на
видимой части одновременно обеих
поверхностей, то эта точка будет
видимая, если хотя бы одна для одной из
поверхностей точка не видима, то и
линия проходящая через эту точку не
видимая.

21.

Взаимное пересечение
поверхностей
Метод секущих
сфер

22.

Частные случаи пересечения
поверхностей вращения
Соосные поверхности - поверхности вращения, имеющие общую
ось вращения.
Теорема: Две соосные поверхности вращения пересекаются по
окружностям- параллелям, число которых равно числу точек
пересечения главных полумеридианов поверхностей.
Все линии пересечения - окружности. На плоскость проекций,
параллельную осям вращения, они проецируются в виде отрезка
прямой линии, соединяющего точки пересечения очерковых
образующих.
¡2
b2
а2
22

23.

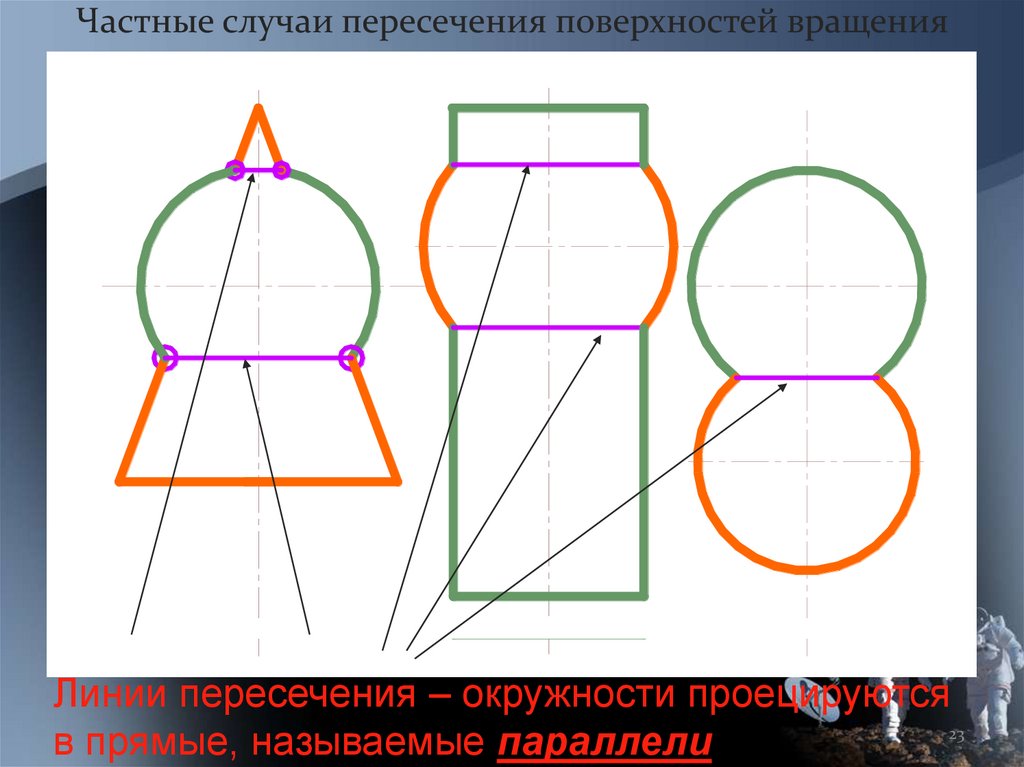
Частные случаи пересечения поверхностей вращения
Линии пересечения – окружности проецируются
23
в прямые, называемые параллели

24.

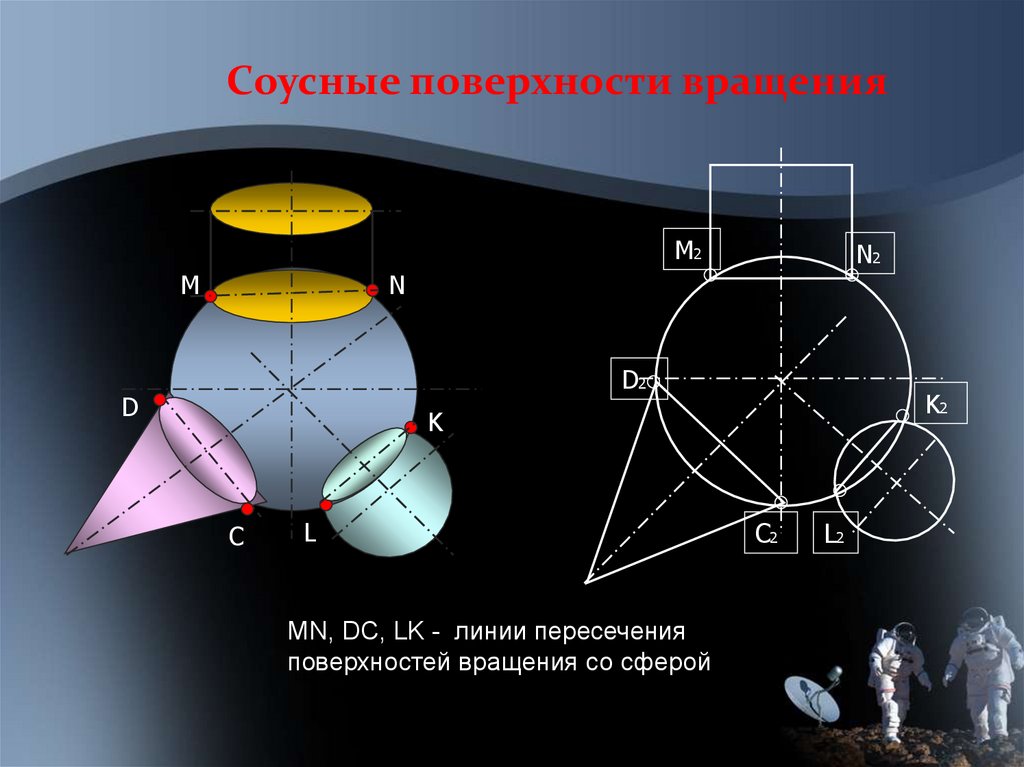
Соусные поверхности вращения
M2
М
N2
N
D2
D
K2
K
С
L
MN, DC, LK - линии пересечения
поверхностей вращения со сферой
C2
L2

25.

Частные случаи пересечения
поверхностей вращения
Теорема Монжа:
две поверхности второго
порядка (квадрики), описанные вокруг третьей
квадрики, пересекаются между собой по двум плоским
кривым
второго
порядка
(коникам),
которые
проецируются на плоскость, параллельную осям
вращения в виде прямолинейных отрезков, соединяющих
точки пересечения очерковых образующих.
25

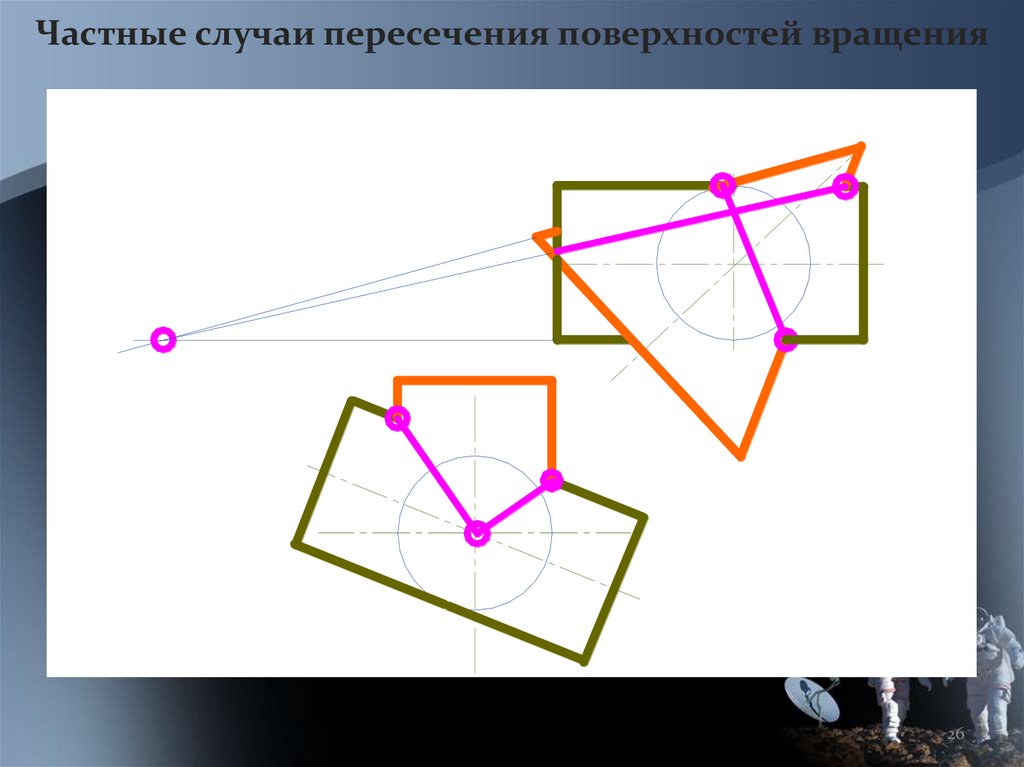
26.

Частные случаи пересечения поверхностей вращения
26

27.

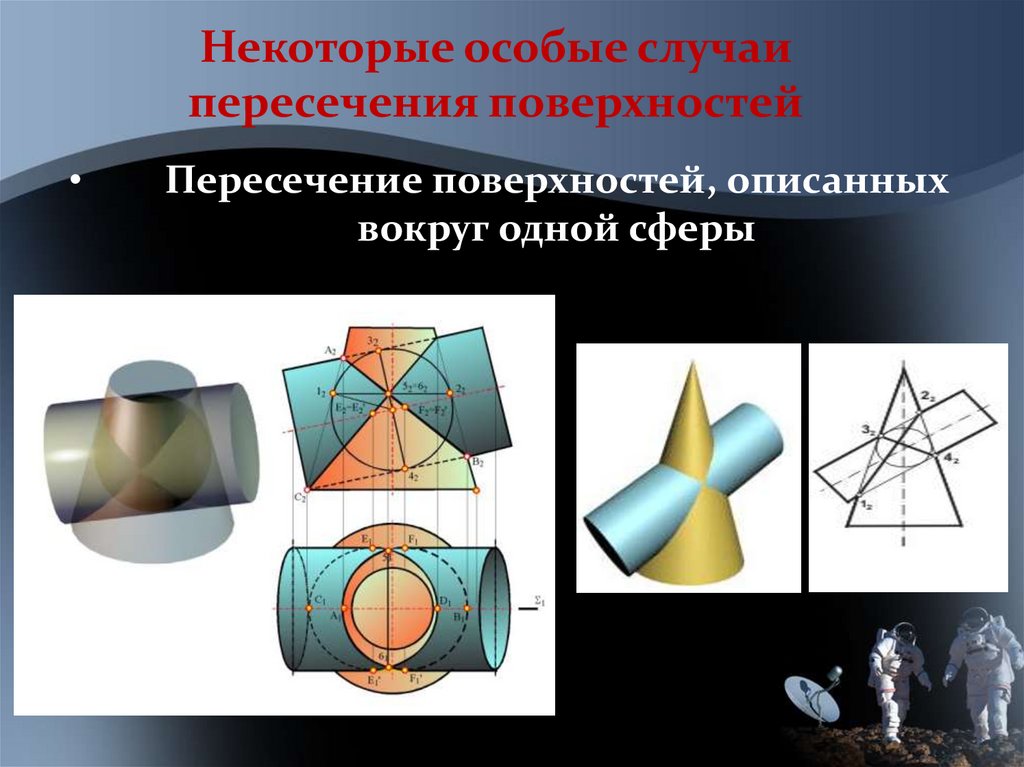
Некоторые особые случаи
пересечения поверхностей
Пересечение поверхностей, описанных
вокруг одной сферы

28.

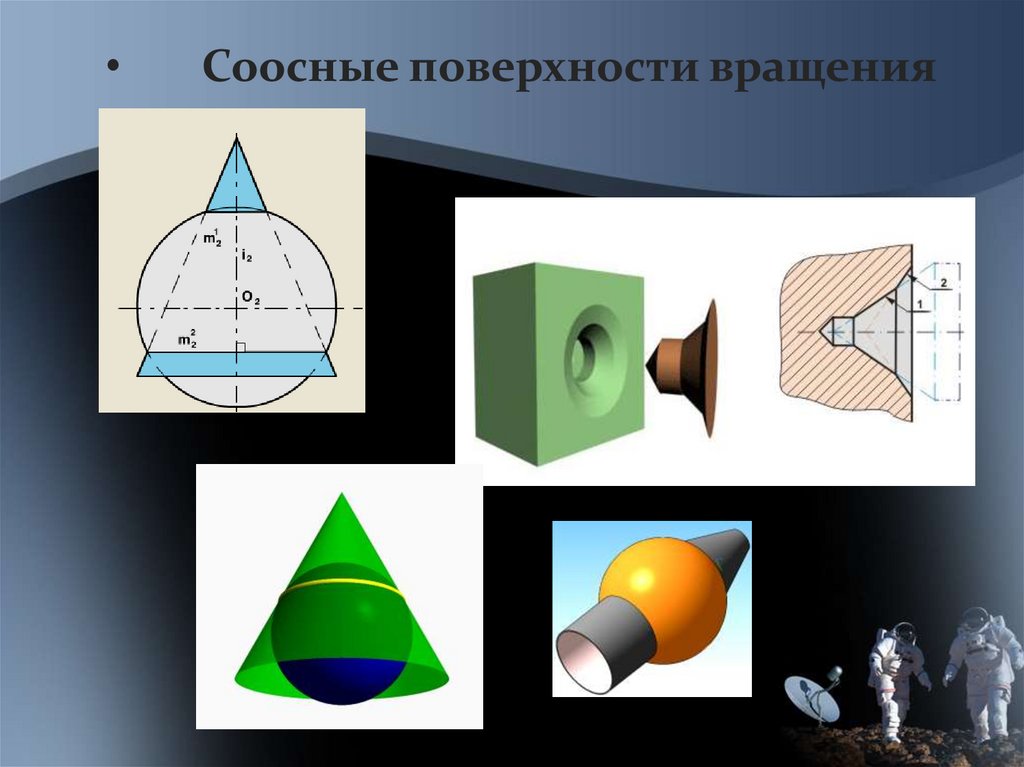
Соосные поверхности вращения

29.

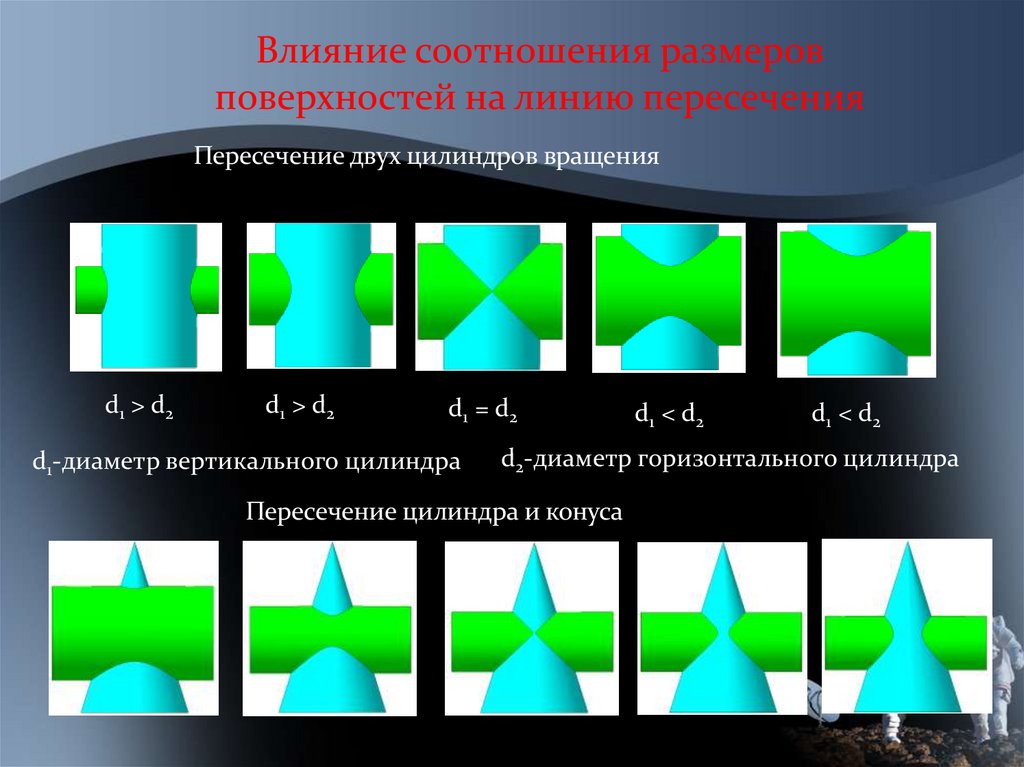
Влияние соотношения размеров
поверхностей на линию пересечения
Пересечение двух цилиндров вращения
d1 > d2
d1 > d2
d1 = d2
d1-диаметр вертикального цилиндра
d1 < d2
d1 < d2
d2-диаметр горизонтального цилиндра
Пересечение цилиндра и конуса

30.

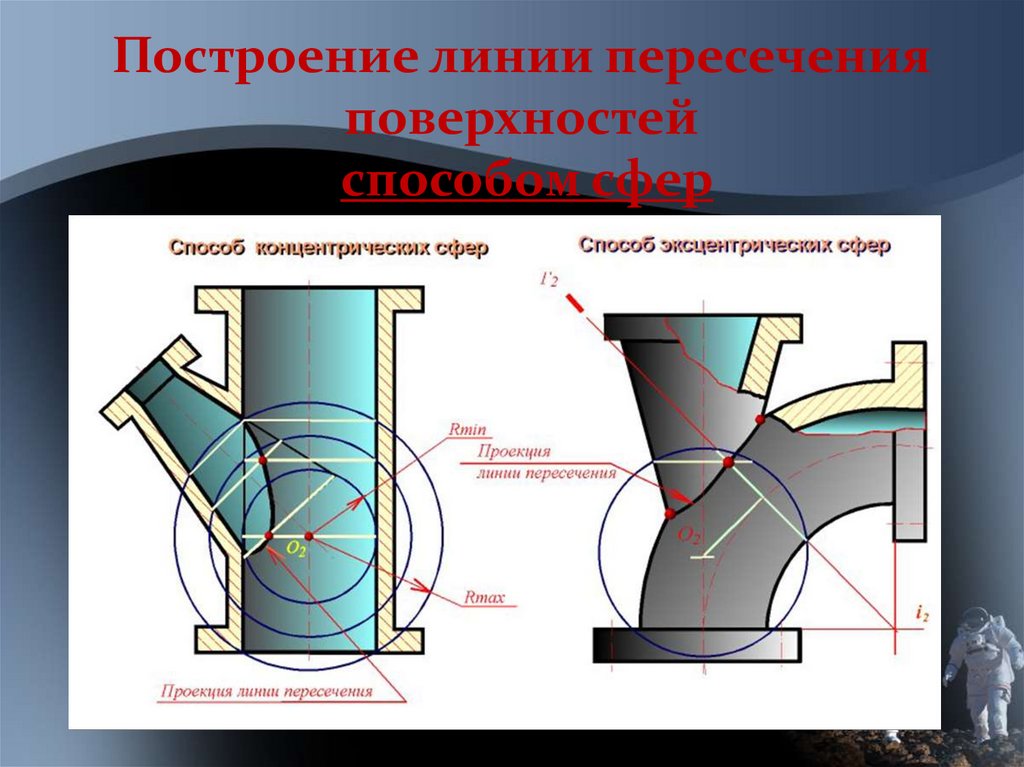
Построение линии пересечения
поверхностей
способом сфер

31.

КОМПЛЕКС УСЛОВИЙ для ПРИМЕНЕНИЯ
СПОСОБА СФЕР :
1. Пересечение только поверхностей вращения.
2.Оси поверхностей пересекаются.
3. Поверхности имеют общую плоскость симметрии,
параллельную одной из плоскостей проекций.
СПОСОБ СФЕР ОСНОВАН НА
СВОЙСТВЕ
СООСНЫХ ПОВЕРХНОСТЕЙ
ПЕРЕСЕКАТЬСЯ ПО
ОКРУЖНОСТЯМ

32.

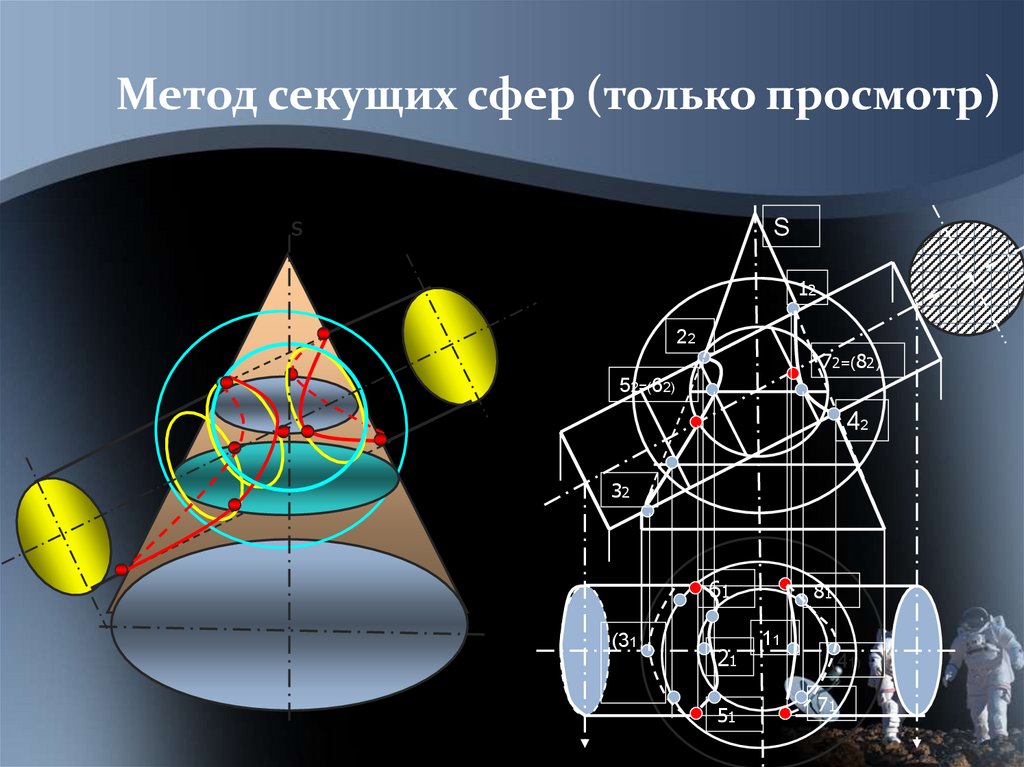
Метод секущих сфер (только просмотр)
s
S
12
22
72=(82)
52=(62)
42
32
61
(31)
21
51
81
11
(41)
71

33.

Применение метода
концентрических сфер возможно при
выполнении следующих условий:
1.Обе поверхности вращения.
2.Оси поверхностей пересекаются.
3.Поверхности
симметрии.
имеют
плоскость
33

34.

Алгоритм решения задач по построению линии
пересечения поверхностей методом
вспомогательных концентрических сфер
1.Провести анализ поверхностей:
• обе поверхности вращения;
• оси поверхностей пересекаются
• поверхности имеют плоскость симметрии.
2. Определить центр вспомогательных
концентрических сфер - это точка пересечения
осей вращения.
3. Определить радиус минимальной вписанной
сферы – Rmin. (Сфера данного радиуса должна
касаться большего из тел и пересекать меньшее из
тел).
34

35.

4. Построить параллель для сферы (Rmin.)
касающейся с большей поверхностью и
параллель (или параллели) для сферы (Rmin.)
пересекающей меньшую поверхность.
5. Найти точки пересечения построенных
параллелей, которые принадлежат линии
пересечения заданных поверхностей.
6. Построить несколько сфер большего
радиуса Rmin< R>Rmax.
7.Определить параллели и точки их
пересечения.
8. Соединить точки плавной линией.
9.Определить
видимость
линий
выполненного изображения.
35

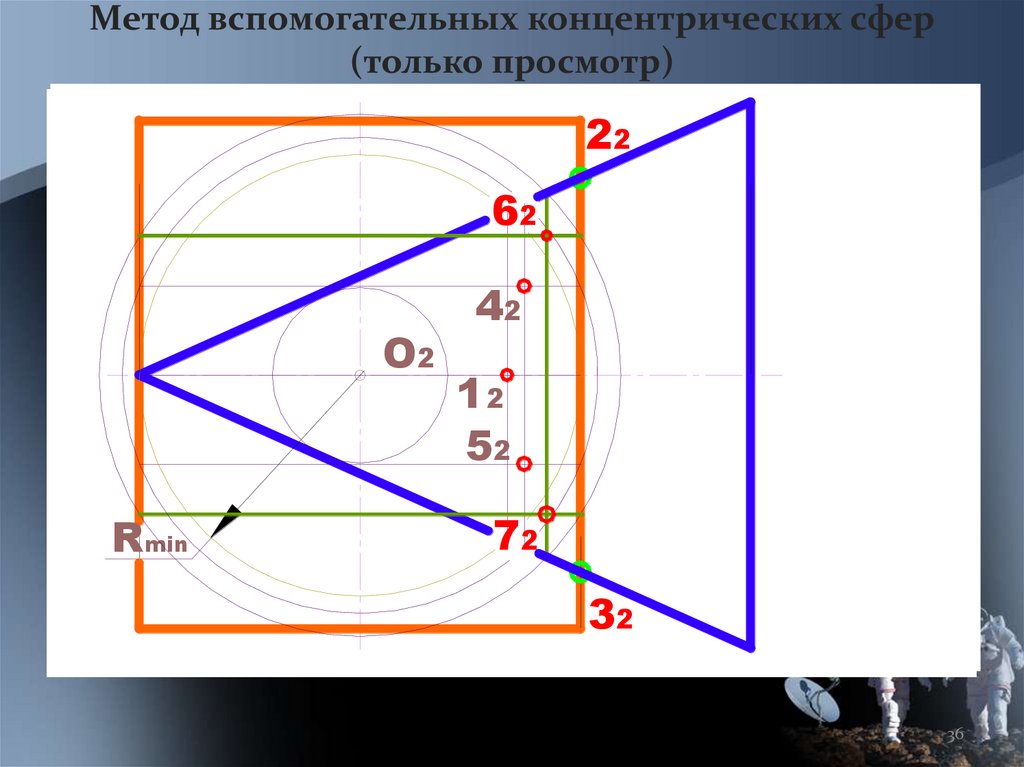
36.

Метод вспомогательных концентрических сфер
(только просмотр)
222
62
O22
Rmin
min
422
122
522
72
322
36

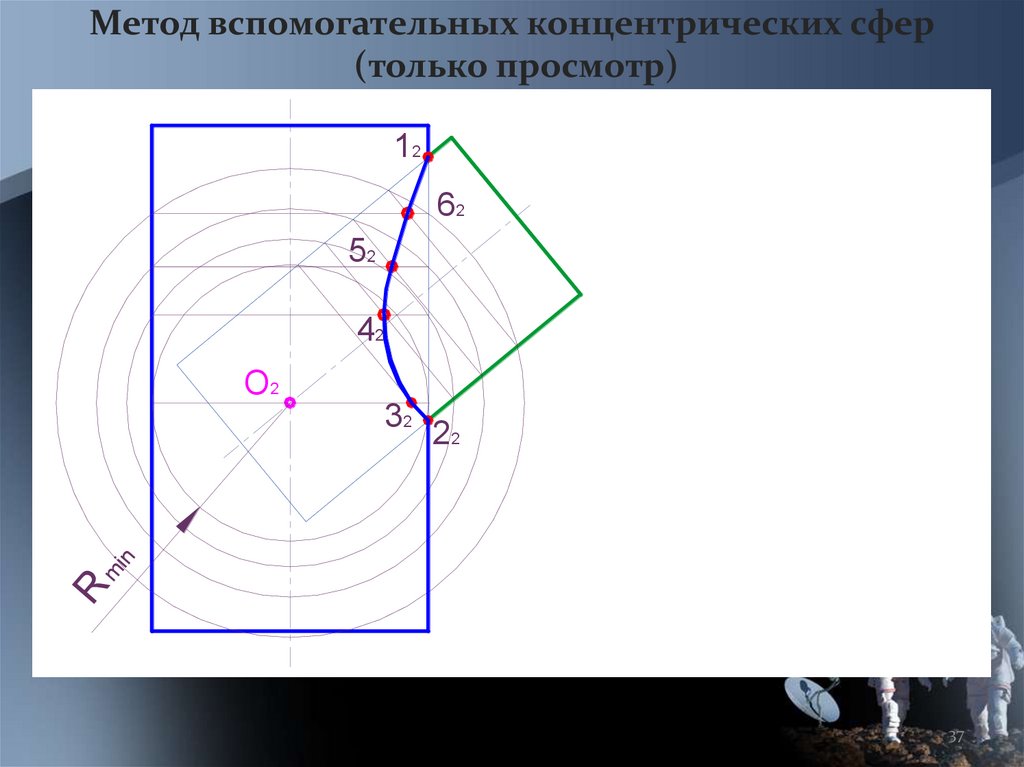
37.

Метод вспомогательных концентрических сфер
(только просмотр)
12
62
52
42
32
22
R
m
in
O
O22
37

38.

ВЫВОДЫ
• Метод концентрических сфер позволяет
в одной проекции построить линию
пересечения двух поверхностей.
• Область использования этого метода
ограничена следующими требованиями:
- обе поверхности должны быть
поверхностями вращения;
- их оси должны пересекаться;
- их оси должны лежать в плоскости
параллельной плоскости проекций.
38

39.

35
Задача: Построить линию
пересечения конуса и
цилиндра
Задача решается
способом сфер
50
R45
1.При решении этой задачи сначала строится
фронтальная проекция линии пересечения, т к
общая плоскость симметрии поверхностей
параллельна фронтальной плоскости проекций.
«Крайние точки сечения - высшая и низшая,
ближайшая и наиболее удаленная точки (точки ,
лежащие на границе видимости относительно
горизонтальной плоскости проекций)
определяются с помощью плоскостей уровня.
Промежуточные точки сечения находятся с
помощью секущих сфер, центр которых
располагается в точке пересечения осей
вращения поверхностей. Сфера минимального
радиуса проводится так, чтобы она касалась
одной поверхности, а вторую пересекала.
Секущие сферы соосны с поверхностью конуса и
цилиндра, а следовательно, пересекаются их по
параллелям.

40.

S2
i2
j2
О2
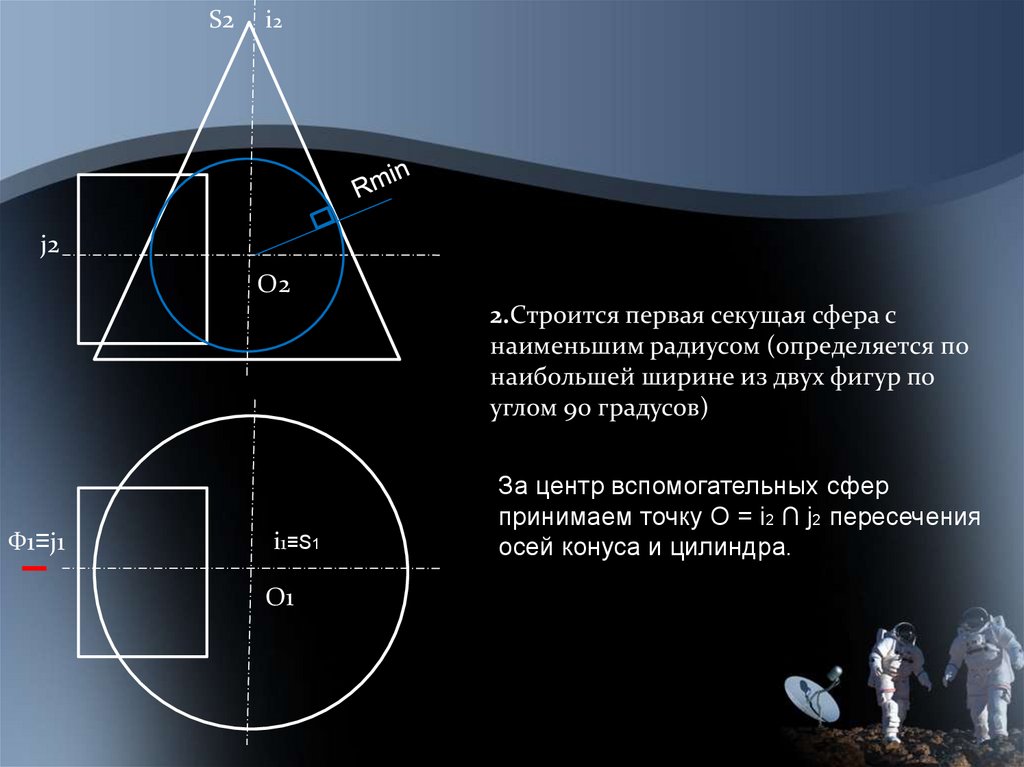
2.Строится первая секущая сфера с
наименьшим радиусом (определяется по
наибольшей ширине из двух фигур по
углом 90 градусов)
Ф1≡j1
i1≡S1
О1
За центр вспомогательных сфер
принимаем точку О = i2 ∩ j2 пересечения
осей конуса и цилиндра.

41.

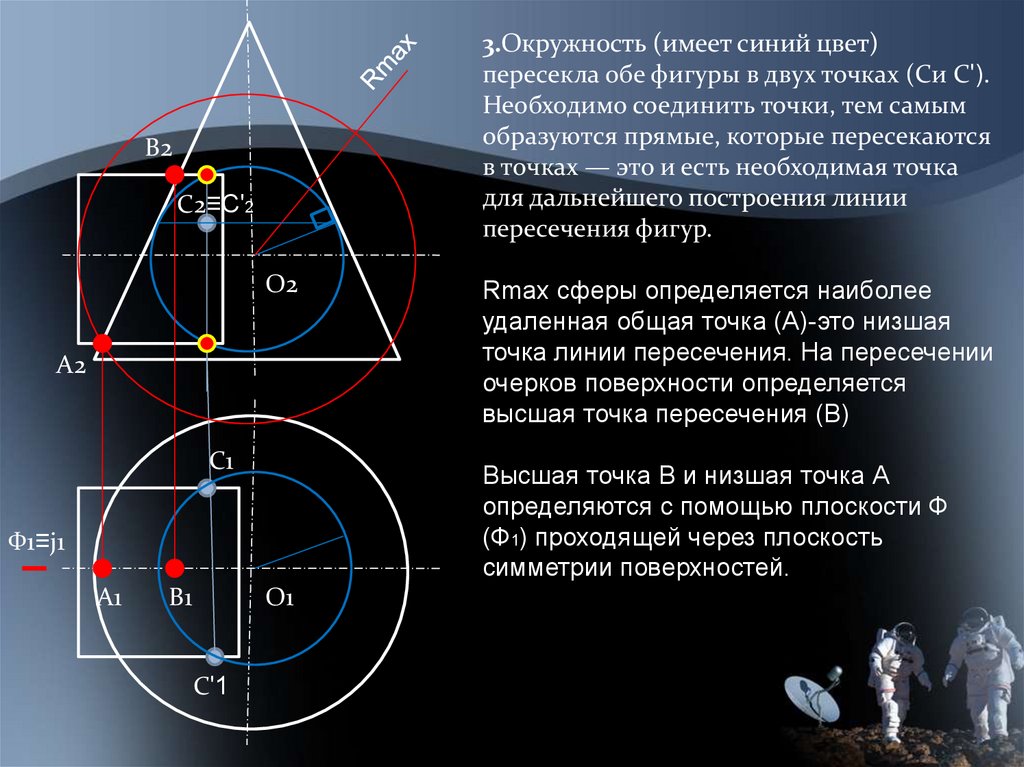
3.Окружность (имеет синий цвет)
пересекла обе фигуры в двух точках (Си Сʹ).
Необходимо соединить точки, тем самым
образуются прямые, которые пересекаются
в точках — это и есть необходимая точка
для дальнейшего построения линии
пересечения фигур.
В2
С2≡Cʹ2
О2
А2
С1
Высшая точка В и низшая точка А
определяются с помощью плоскости Ф
(Ф1) проходящей через плоскость
симметрии поверхностей.
Ф1≡j1
А1
В1
О1
Сʹ1
Rmax сферы определяется наиболее
удаленная общая точка (А)-это низшая
точка линии пересечения. На пересечении
очерков поверхности определяется
высшая точка пересечения (В)

42.

В2
С2≡Cʹ2
D2≡Dʹ2
RD
Г2≡i2
О2
А2
D1
С1
Ф1≡j1
А1
В1
Dʹ1 Сʹ1
О1
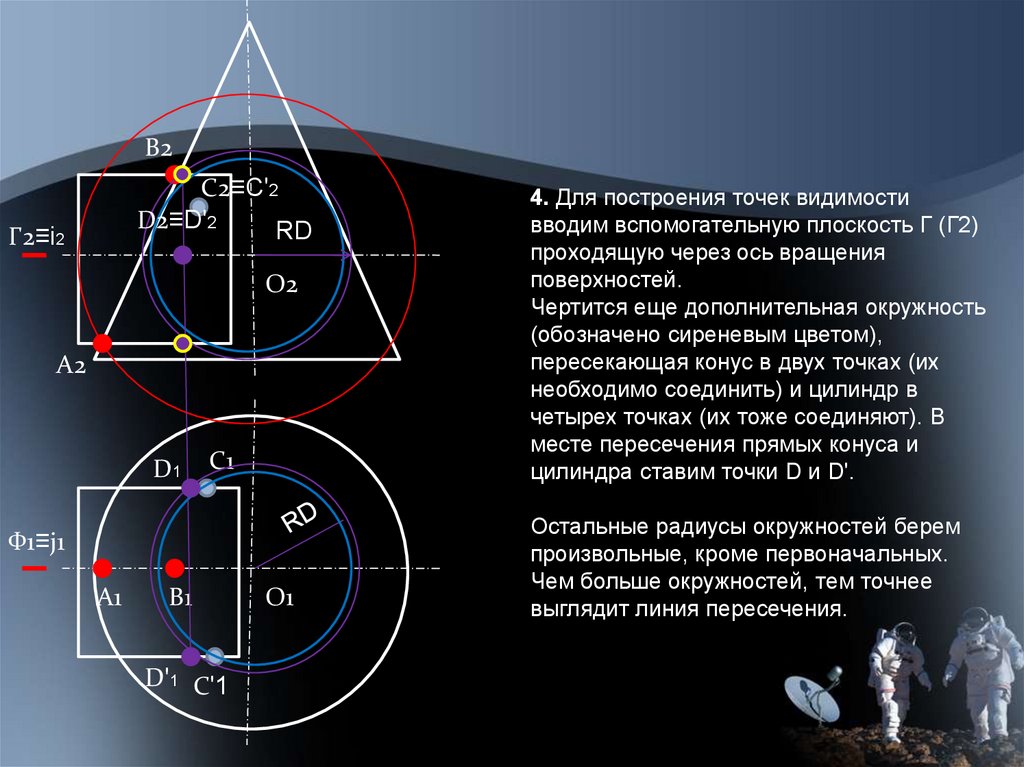
4. Для построения точек видимости
вводим вспомогательную плоскость Г (Г2)
проходящую через ось вращения
поверхностей.
Чертится еще дополнительная окружность
(обозначено сиреневым цветом),
пересекающая конус в двух точках (их
необходимо соединить) и цилиндр в
четырех точках (их тоже соединяют). В
месте пересечения прямых конуса и
цилиндра ставим точки D и Dʹ.
Остальные радиусы окружностей берем
произвольные, кроме первоначальных.
Чем больше окружностей, тем точнее
выглядит линия пересечения.

43.

В2
С2≡Cʹ2
Г2≡i2
D2≡Dʹ2
О2
Е2≡Еʹ2
А2
С1
Ф1≡j1
Е1 D1
А1
Еʹ1
В1
О1
Dʹ1
Сʹ1
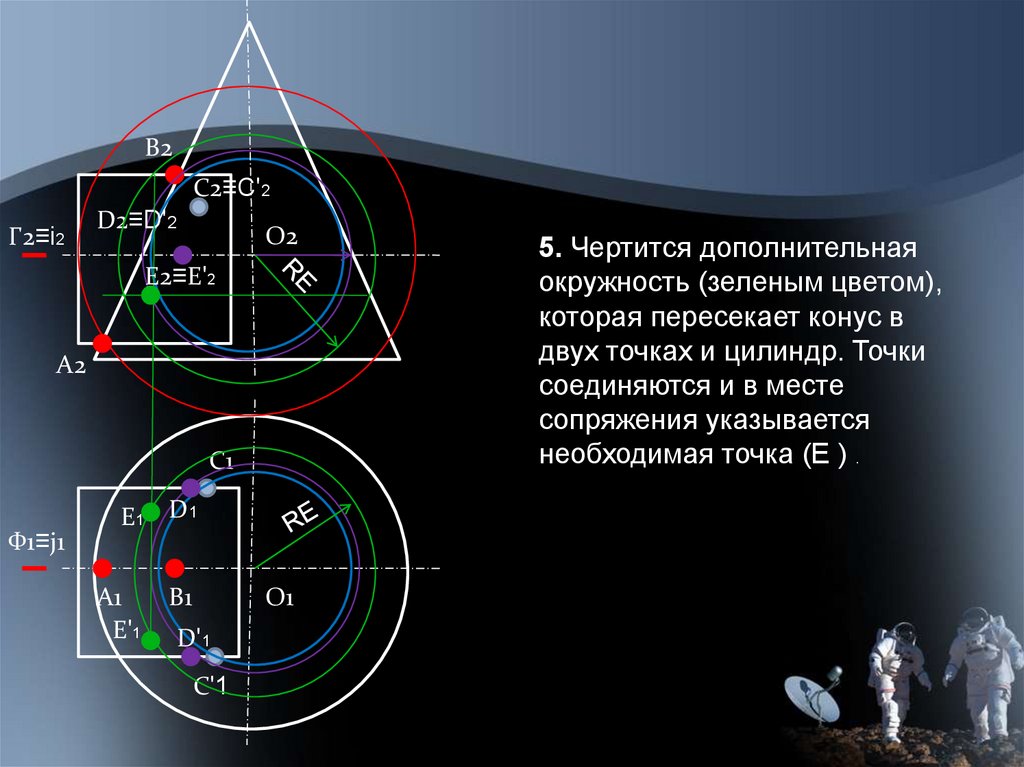
5. Чертится дополнительная
окружность (зеленым цветом),
которая пересекает конус в
двух точках и цилиндр. Точки
соединяются и в месте
сопряжения указывается
необходимая точка (Е ) .

44.

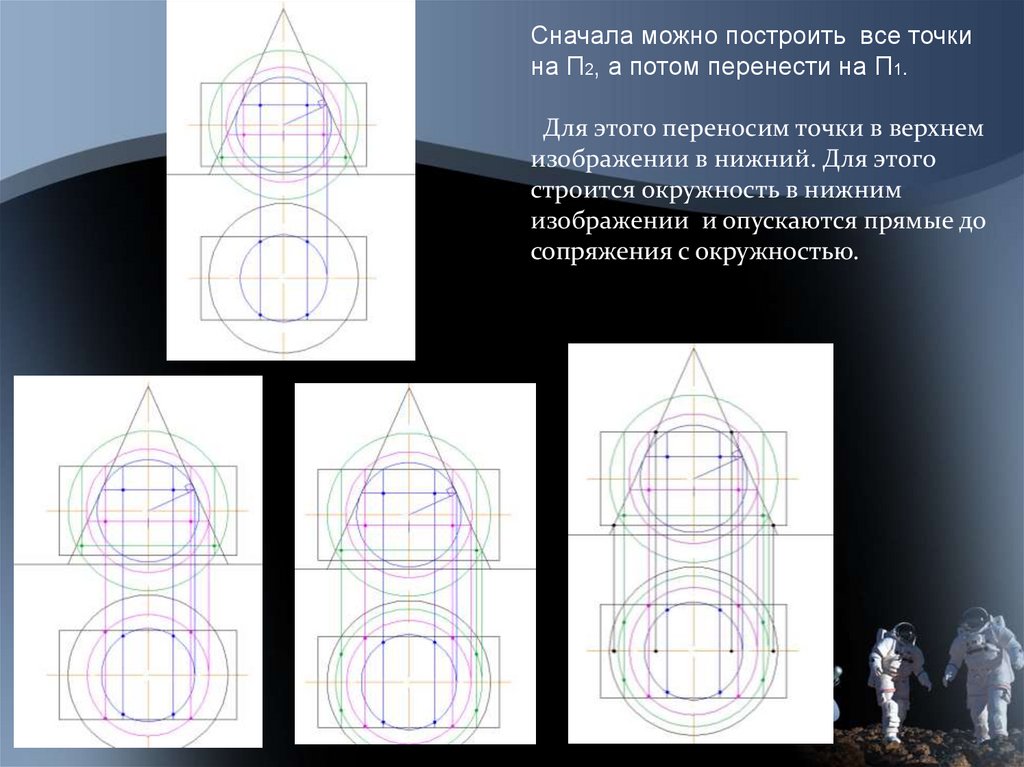
Сначала можно построить все точки
на П2, а потом перенести на П1.
Для этого переносим точки в верхнем
изображении в нижний. Для этого
строится окружность в нижним
изображении и опускаются прямые до
сопряжения с окружностью.

45.

В2
Г2≡i2
С2≡Cʹ2
D2≡Dʹ2
О2
Е2≡Еʹ2
А2
С1
Ф1≡j1
Е1 D1
А1
В1
Еʹ1 Dʹ1
Сʹ1
О1
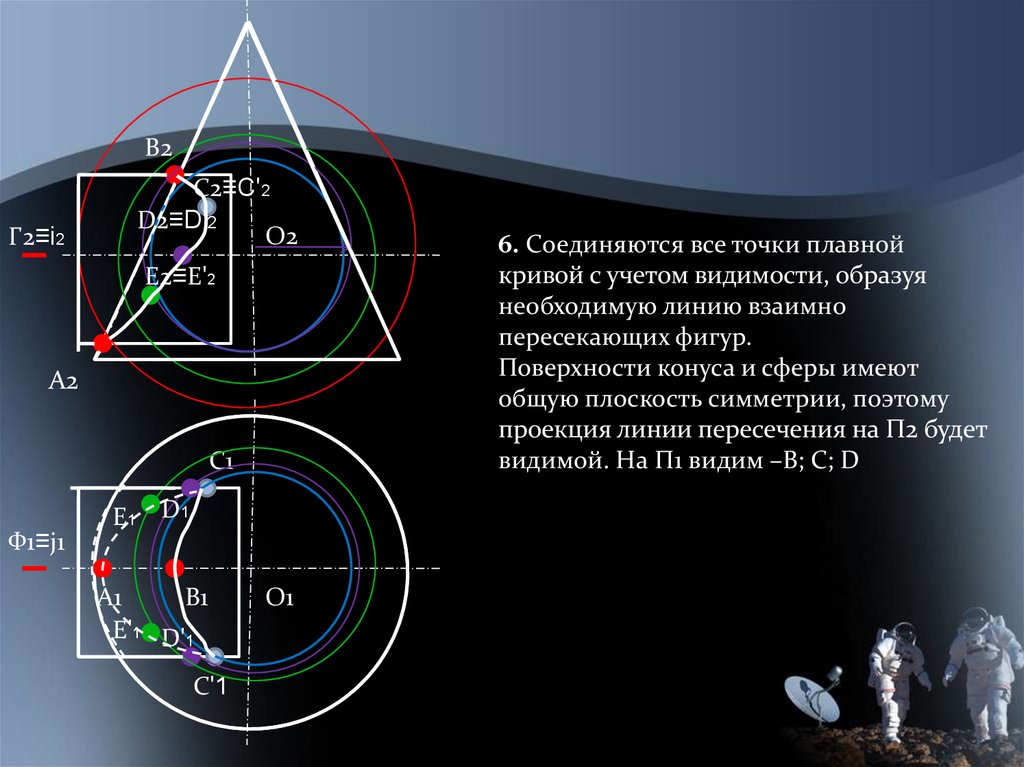
6. Соединяются все точки плавной
кривой с учетом видимости, образуя
необходимую линию взаимно
пересекающих фигур.
Поверхности конуса и сферы имеют
общую плоскость симметрии, поэтому
проекция линии пересечения на П2 будет
видимой. На П1 видим –В; С; D

46.

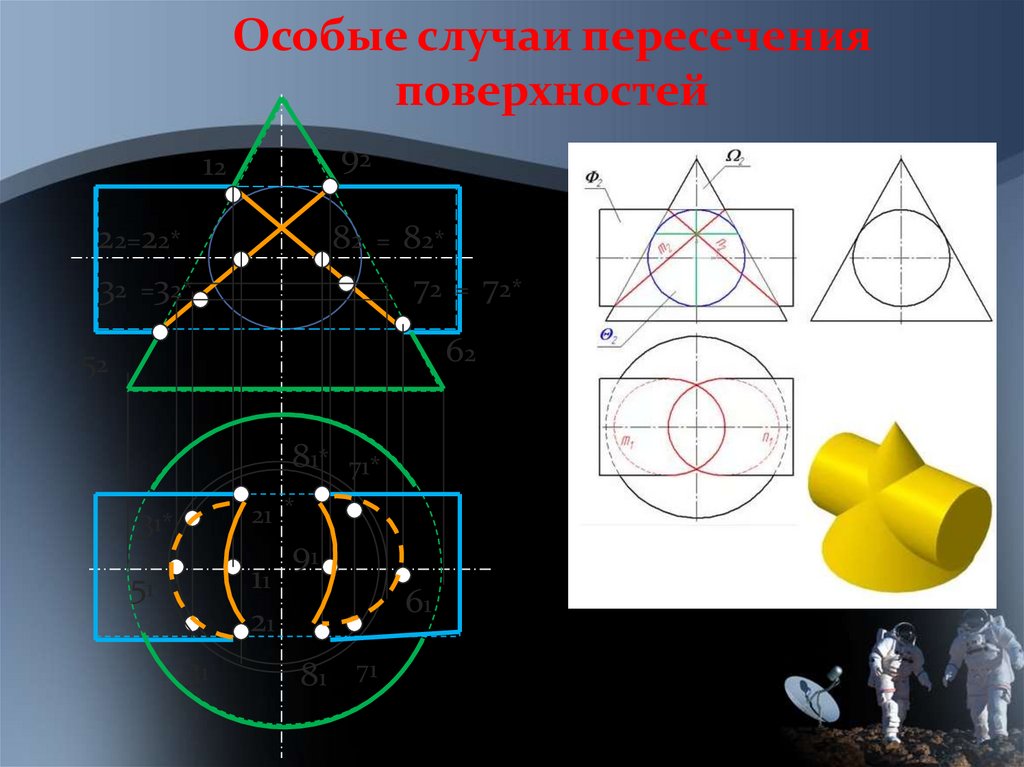
Особые случаи пересечения
поверхностей
92
12
22=22*
32 =32*
82
=
82*
72 = 72*
62
52
81*
71*
21 *
31*
11
21
51
31
91
61
81
71

47.

Спасибо за внимание!
Желаю успехов!