Планирование многофакторного экпримента

1.

Планирование многофакторного эксперимента
Планирование
многофакторного
эксперимента
позволяет
определить с помощью оптимального количества опытов влияние
разных факторов в многофакторном эксперименте; оценить
значимость каждого фактора и определить пути достижения
наилучшего результата.
Число опытов N определяется выражением N= 2n, где n – количество факторов
Факторы,
резко отличающиеся количественно, в теории ПФЭ
кодируются цифрами -1 и +1 для нижнего и верхнего уровней,
соответственно
Проводятся малые серии экспериментов, в которых по
определенному закону меняются все факторы: по результатам
первой серии выбирается направление изменения факторов во 2-о
серии и т.д., таким образом, последовательно, шаг за шагом
приближаемся к оптимуму.
Метод Бокса и Уинстема – итерационный метод, метод
последовательного приближения

2.

Планирование позволяет:
1) Сократить число опытов
2) Разработать алгоритм, позволяющий одновременно изменять все факторы
3) Оценить значимость (влияние) каждого фактора
4) Оценить эффективность выбранного пути
5) Оценить точность попадания в оптимум
Пусть интересующее нас свойство (Y) объекта зависит от нескольких (п)
независимых переменных {X1, Х2, ..., Хп), и мы хотим выяснить характер
этой зависимости - Y=f(X1, X2, ..., Xn), о которой мы имеем лишь общее
представление. Величина Y - называется "отклик", а сама зависимость
Y=f(X1, X2, ..., Xn - "функция отклика« или параметр оптимизации.
X1, Х2, ..., Хп
Независимые переменные, отражающие способы
влияния на объект
. Они должны быть:
1) управляемым (т.е. их значения можно удерживать на нужном
уровне сколь угодно долго)
2) иметь область определения (min и max значения
3 ) быть независимыми друг от друга
4) могут быть как качественными, так и количественными

3.

Функция (функции) отклика – это зависимые переменные, количественно
характеризующие цель исследования.
Они должны:
1) иметь область определения
2) быть однозначными, т.е. определенному сочетанию факторов должна
соответствовать единственная величина параметра оптимизации
3) быть легко измеряемыми
4) иметь физический смысл
Полный факторный эксперимент ПФЭ
N= 2n
ПФЭ называется такой эксперимент, в котором реализуются все
возможные сочетания уровней факторов
Приступая к эксперименту необходимо:
1) определить область определения факторов
2) выбрать исходную точку в факторном пространстве (внутри его, а не на
краю). Эта исходная точка называется основным уровнем
эксперимента
3) выбрать интервал варьирования каждого фактора
4) Перейти к кодированию факторов

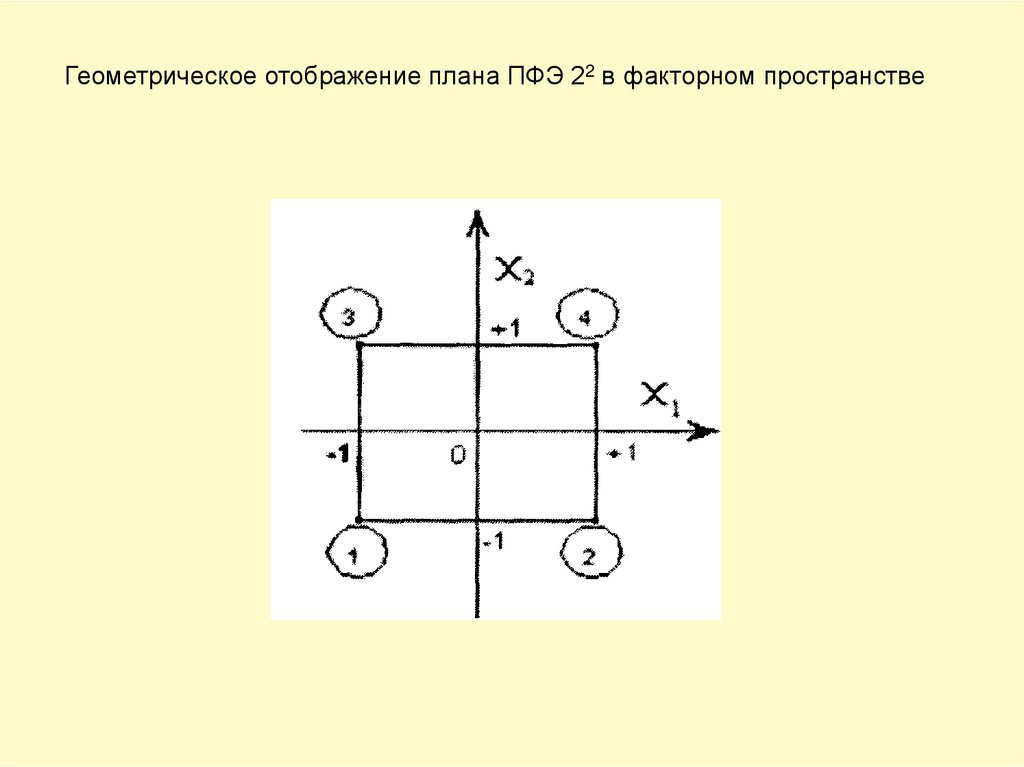
4.

Геометрическое отображение плана ПФЭ 22 в факторном пространстве

5.

Функция отклика может быть выражена через кодированные факторы
y=f(x1,..., хn), она должна быть непрерывной, поверхность отклика – гладкой,
и должен существовать единственный экстремум. Этими свойствами
обладают степенные функции в виде полинома:
y=bo+b1x1+b2x2+... +bnxn+b12x1x2+... +bnn-1.!xn-1.!xn+b11x12 +…bnnxn2+….(
На крутых склонах поверхности отклика вдали от экстремума, т.е. в
области восхождения по градиенту, можно ограничиться линейными и
смешанными членами полинома.

6.

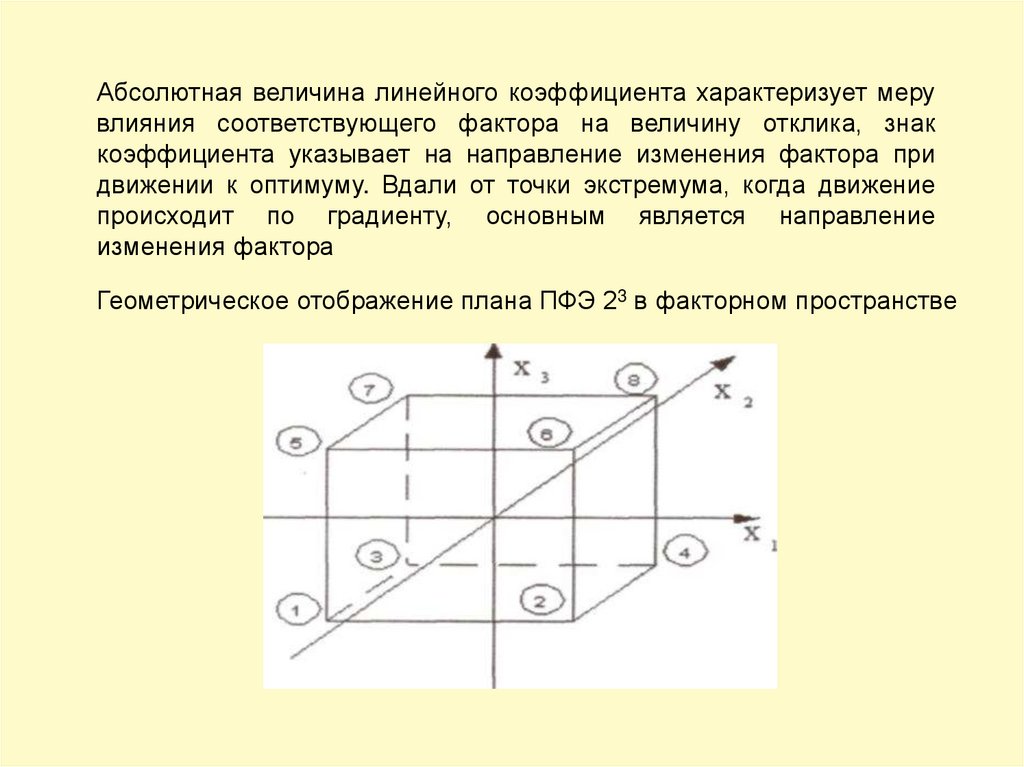
Абсолютная величина линейного коэффициента характеризует меру
влияния соответствующего фактора на величину отклика, знак
коэффициента указывает на направление изменения фактора при
движении к оптимуму. Вдали от точки экстремума, когда движение
происходит по градиенту, основным является направление
изменения фактора
Геометрическое отображение плана ПФЭ 23 в факторном пространстве

7.

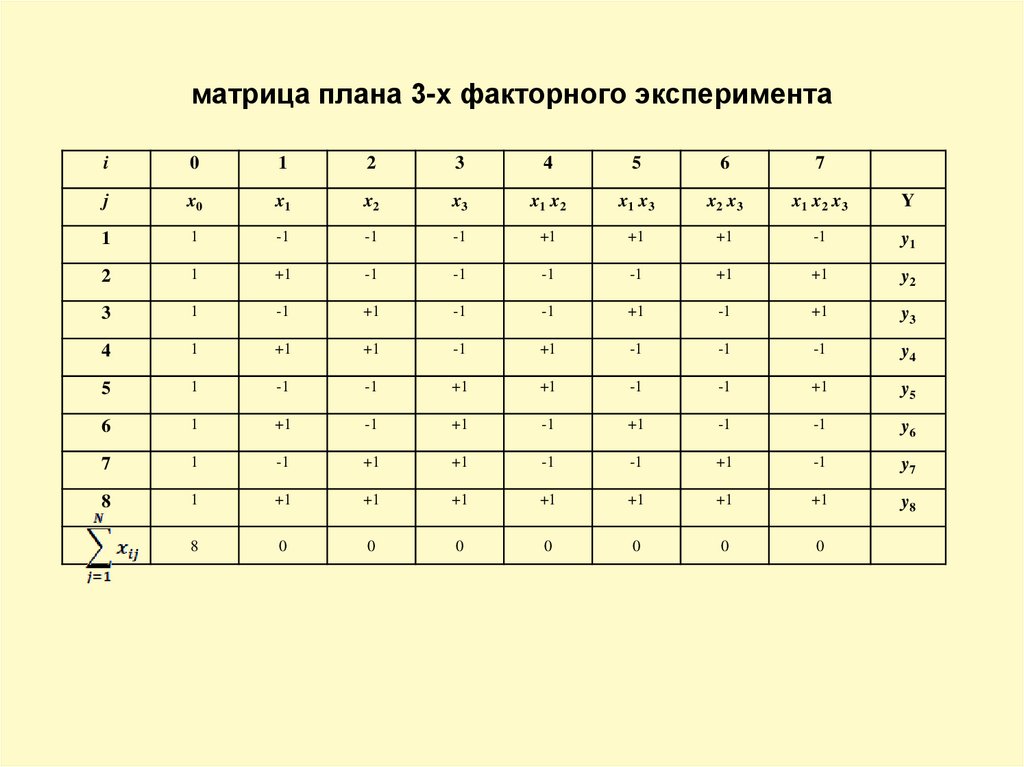
матрица плана 3-х факторного эксперимента
i
0
1
2
3
4
5
6
7
j
x0
x1
x2
x3
x1 x2
x1 x3
x2 x3
x1 x2 x3
Y
1
1
-1
-1
-1
+1
+1
+1
-1
y1
2
1
+1
-1
-1
-1
-1
+1
+1
y2
3
1
-1
+1
-1
-1
+1
-1
+1
y3
4
1
+1
+1
-1
+1
-1
-1
-1
y4
5
1
-1
-1
+1
+1
-1
-1
+1
y5
6
1
+1
-1
+1
-1
+1
-1
-1
y6
7
1
-1
+1
+1
-1
-1
+1
-1
y7
8
1
+1
+1
+1
+1
+1
+1
+1
y8
8
0
0
0
0
0
0
0

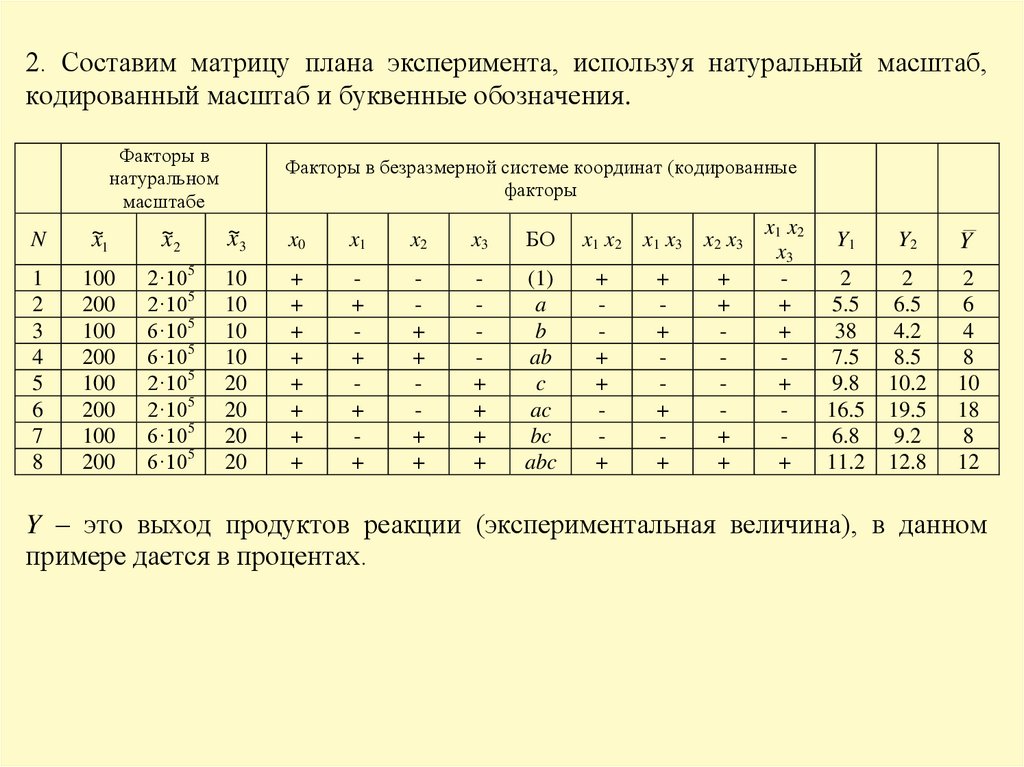
8.

Полином, ограниченный линейными и смешанными членами, имеет вид:
Для расчета любого коэффициента данного полинома необходимо
перемножить
столбец
функции
отклика
и
столбец
матрицы,
соответствующий данному фактору или сочетанию факторов, а полученную
сумму разделить на число опытов (в 3-х факторном эксперименте N=8):

9.

Значимость любого коэффициента можно проверить по критерию
Стьюдента. Коэффициент считается значимым, если значение
расчетного критерия оказывается больше, чем значение табличного
критерия, определенного для соответствующей доверительной
вероятности и степени свободы
t
расч
i
t
табл
p 0.95
f N ( m 1)
m – количество параллельных опытов
После проверки незначимые коэффициенты отбрасывают.
Величина расчетного критерия Стьюдента определяется по формуле
t
расч
i
bi
(bi )
погрешность определения любого коэффициента
. В ПФЭ все коэффициенты определяются с одинаковой точностью

10.

В зависимости от условий проведения эксперимента величина
определяется двумя способами
1 способ.
Для каждой комбинации значений параметров оптимизации проводят m
параллельных опытов,определяют дисперсии функции отклика