Введение в планирование эксперимента. Полный факторный эксперимент 2k (лекция 1)

1.

Лекция 1. Введение в планирование
эксперимента. Полный факторный
эксперимент 2k

2.

Введение в планирование эксперимента
Планирование эксперимента – процедура поиска числа условий
(параметров), наилучших (необходимых и достаточных) для достижения
поставленной цели с требуемой точностью.
Допущения:
1. Математическая модель процесса заранее неизвестна, то есть
представляется в виде «чёрного ящика»;
2. Существует только один параметр оптимизации y;
3. Множество параметров, влияющих на показатель качества параметра
оптимизации y, задано и называется факторами xi;
4. Возможные сочетания факторов не зависят друг от друга, равноценны и
реализуемы.
2

3.

Введение в планирование эксперимента
В результате проведения экспериментов может быть получена эмпирическая
зависимость:
y = f(x1, x2, …, xn) – функция (поверхность) отклика
Одна из основных задач, которые решаются при планировании эксперимента –
минимизация числа опытов.
Планирование эксперимента – это процедура выбора условий (и количества
опытов), минимально необходимых для решения поставленной задачи.
3

4.

Введение в планирование эксперимента
Требования, предъявляемые к параметру оптимизации:
1. Параметр оптимизации должен быть количественным и характеризоваться
одним числом;
2. Должен быть универсальным;
3. Должен иметь физический смысл и быть легко вычисляемым (легко
измеряемым).
Требования, предъявляемые к факторам:
1. Факторы должны быть независимы и управляемы;
2. Точность замера должна быть максимально возможной;
3. Должны быть совместимы.
4

5.

Выбор модели эксперимента
Задача состоит в том, чтобы определить вид функции (поверхности) отклика
(её математическую формулу), а затем найти коэффициенты функции отклика
(коэффициент регрессии).
Модель надо выбрать таким образом, чтобы избежать полного перебора
факторов xi и минимизировать количество опытов N.
Допустим, что параметр оптимизации y зависит
от двух факторов х1 и х2. Пусть реально
поверхность отклика представляет собой
параболоид.
Данная поверхность отклика может быть
получена:
1. Полным перебором факторов;
5

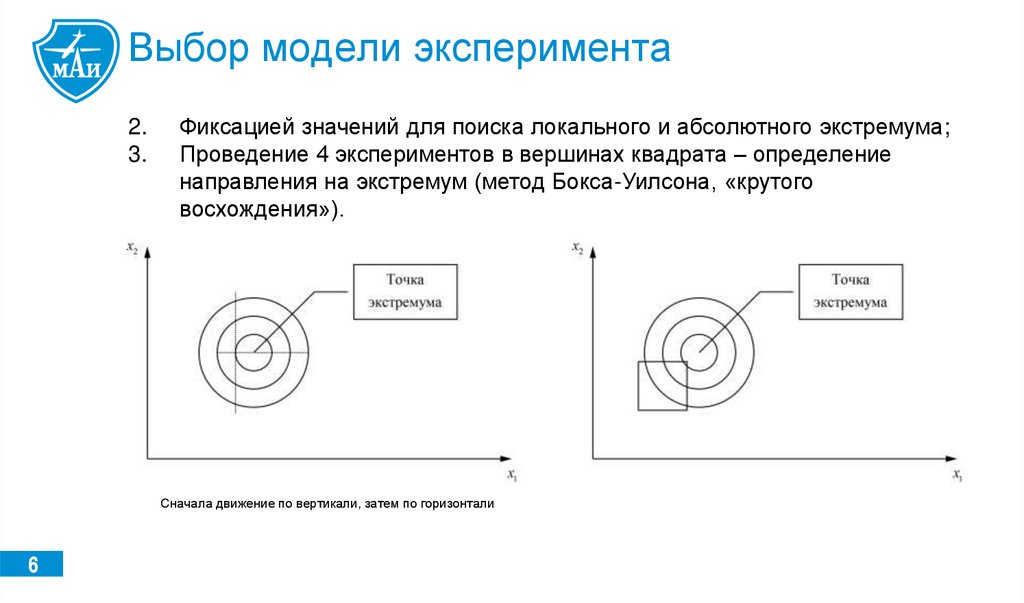
6.

Выбор модели эксперимента
2.
3.
Фиксацией значений для поиска локального и абсолютного экстремума;
Проведение 4 экспериментов в вершинах квадрата – определение
направления на экстремум (метод Бокса-Уилсона, «крутого
восхождения»).
Сначала движение по вертикали, затем по горизонтали
6

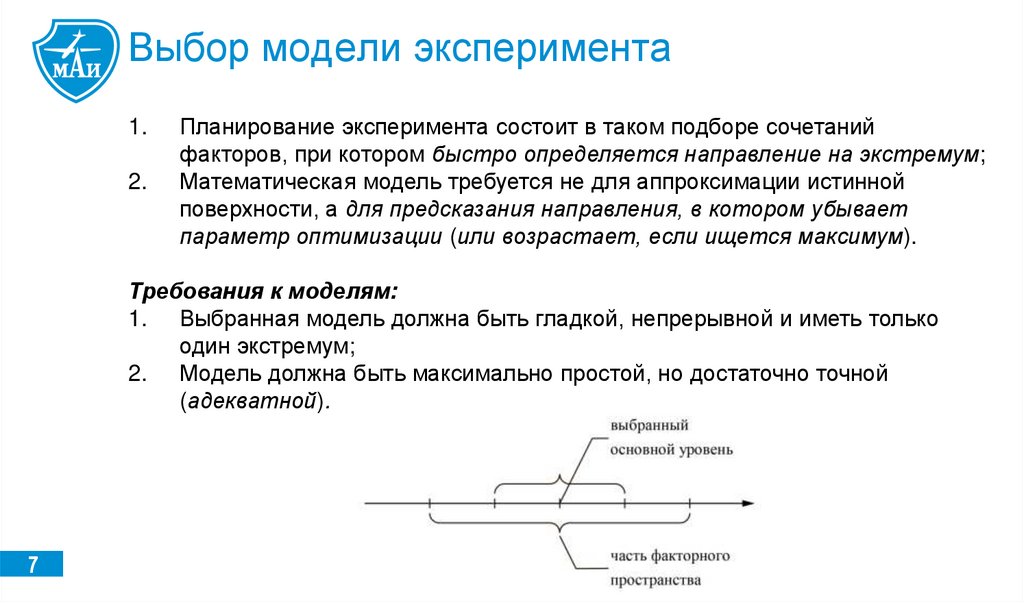
7.

Выбор модели эксперимента
1.
2.
Планирование эксперимента состоит в таком подборе сочетаний
факторов, при котором быстро определяется направление на экстремум;
Математическая модель требуется не для аппроксимации истинной
поверхности, а для предсказания направления, в котором убывает
параметр оптимизации (или возрастает, если ищется максимум).
Требования к моделям:
1. Выбранная модель должна быть гладкой, непрерывной и иметь только
один экстремум;
2. Модель должна быть максимально простой, но достаточно точной
(адекватной).
7

8.

Выбор модели эксперимента
Функции отклика:
1. Полиномиальные;
2. Неполная квадратная;
3. Линейная.
y b0 b1 x1 b2 x2 b3 x3 b12 x1 x2 b13 x1 x3 b23 x2 x3 b123 x1 x2 x3 b11 x12 b22 x22 b33 x32 .
y = b0 + b1x1 + b2x2 + b3x3 + b12x1x2 + b13x1x3 + b23x2x3 + b123x1x2x3.
y = b0 + b1x1 + b2x2 + b3x3.
8

9.

Полный факторный эксперимент 2k
Полный факторный эксперимент (ПФЭ) – эксперимент, в котором
реализуются все возможные сочетания уровней факторов.
Уровень фактора – значение, которое может принимать фактор в одном из
опытов.
Процесс исследования при помощи ПФЭ:
1. Неформальные этапы;
2. Принятие интуитивных решений;
3. Формальные (формализованные) этапы (расчёты).
9

10.

Полный факторный эксперимент 2k
Неформальные этапы:
1. Выбор факторного пространства;
2. Выбор количества уровней варьирования факторов;
3. Выбор интервалов варьирования факторов.
Интервал варьирования – число, от прибавления которого у основному
уровню получается верхняя граница интервала варьирования, от вычитания
нижняя граница.
10

11.

Полный факторный эксперимент 2k
Формальные этапы:
1. Кодирование факторов;
2. Составление матрицы плана;
3. Проверка выполнения свойств ПФЭ;
4. Определение коэффициентов функции отклика.
Кодирование факторов:
X X 0i
xi i
,
ni
максимальное значение xmax = +(1),
минимальное значение xmin = −(1),
основной уровень x0 = 0.
где Xi – натуральное значение фактора, X0i – натуральное значение основного
уровня фактора, ni – интервал варьирования.
11

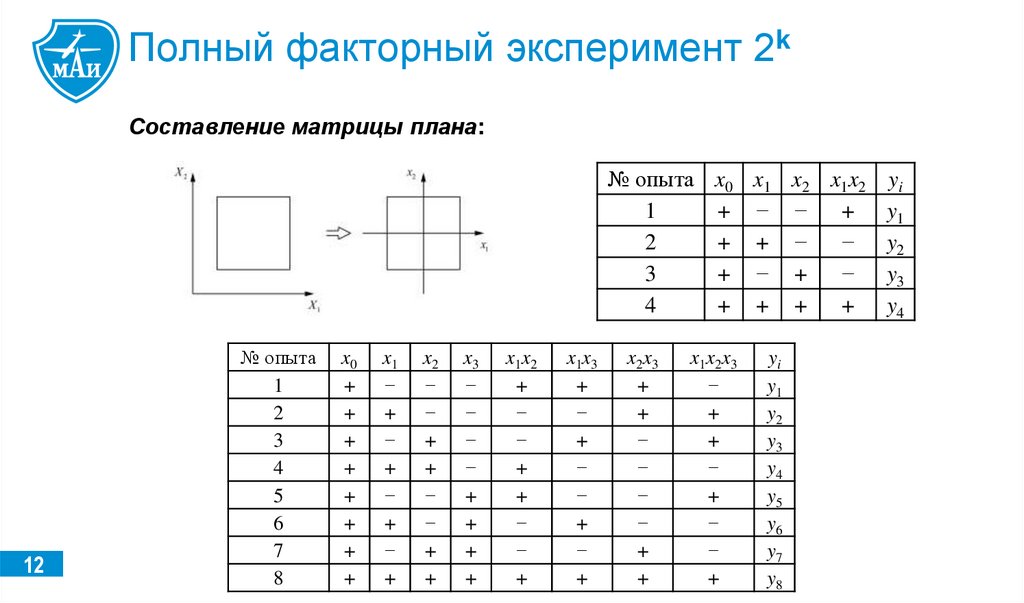
12.

Полный факторный эксперимент 2k
Составление матрицы плана:
№ опыта x0 x1 x2 x1x2
1
+ − −
+
2
+ + −
−
3
+ − +
−
4
+ + +
+
12
№ опыта
1
2
3
4
5
6
7
8
x0
+
+
+
+
+
+
+
+
x1
−
+
−
+
−
+
−
+
x2
−
−
+
+
−
−
+
+
x3
−
−
−
−
+
+
+
+
x1x2
+
−
−
+
+
−
−
+
x1x3
+
−
+
−
−
+
−
+
x2x3
+
+
−
−
−
−
+
+
x1x2x3
−
+
+
−
+
−
−
+
yi
y1
y2
y3
y4
y5
y6
y7
y8
yi
y1
y2
y3
y4

13.

Полный факторный эксперимент 2k
Проверка выполнения свойств ПФЭ:
N
x 0 – симметричность;
j 1
ij
N
x N – нормировка;
j 1
2
ij
N
( x x ) 0 – ортогональность;
j 1
ij
pj
Ротатабельность – точность предсказания значений параметра одинакова на
равных расстояниях от центра эксперимента и не зависит от направления.
13

14.

Полный факторный эксперимент 2k
Определение коэффициентов функции отклика:
1 N
bi ( xij y j ), i 0...k .
N j 1
1 N
bip ( xij x pj y j ), i 1...k ; p 1...k .
N j 1
14