Похожие презентации:
Корреляционный анализ. Лекция 9
1. ЛЕКЦИЯ 9
КОРРЕЛЯЦИОННЫЙАНАЛИЗ
2. 9.1. Зависимости, встречающиеся в природе
3. Основные типы зависимостей между переменными:
• Функциональные2
(например, S = πr );
• Корреляционные
(=статистические)
4. Корреляционные зависимости
значению одного признака соответствуетцелая гамма значений другого признака
выявляются только на групповых объектах
с применением методов статистики
5. Задача корреляционного анализа:
…установить форму,направление
и тесноту связи, а также
оценить ее статистическую
значимость.
6. 9.2. Коэффициент корреляции
7. Показатель ковариации:
1Cov [ ( xi x )( yi y )]
n
Недостаток: предполагается,
что оба признака выражаются
в одинаковых единицах.
8. Коэффициент корреляции Пирсона:
n1
( xi x )( yi y )
n i 1
r
sx s y
n
( x x )( y y )
r
(x x) ( y y)
i
i 1
i
2
i
i
2
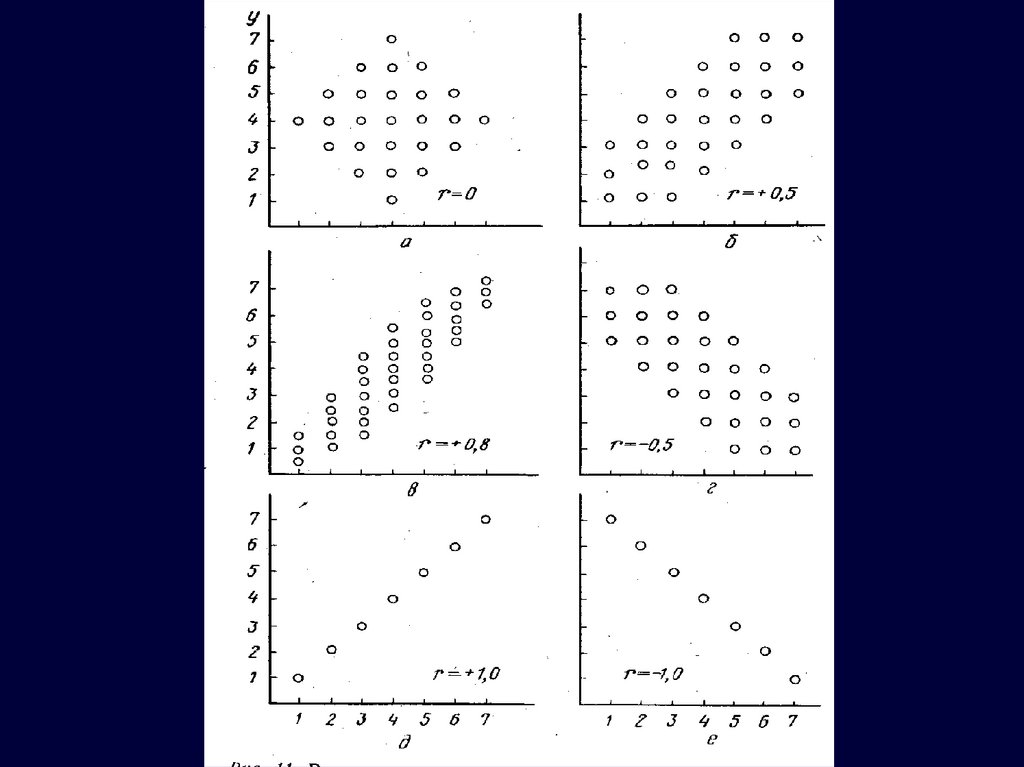
9. Пределы колебаний коэффициента корреляции:
-1 ≤ r ≤ +110.
11. Интерпретация коэффициента корреляции:
|r| > 0.7 - тесная связь;|r| = 0.5 – 0.6 - зависимость
средней степени;
|r| < 0,4 – слабая связь.
12. Недостаток коэффициента корреляции Пирсона:
характеризует лишь линейныезависимости между нормально
распределенными признаками…
13. 9.3. Статистическая значимость коэффициента корреляции
14. Стандартная ошибка коэффициента корреляции при больших n:
1 rsr
n
2
15. Стандартная ошибка коэффициента корреляции при n < 100:
Стандартная ошибкакоэффициента корреляции
при n < 100:
1 r
sr
n 2
2
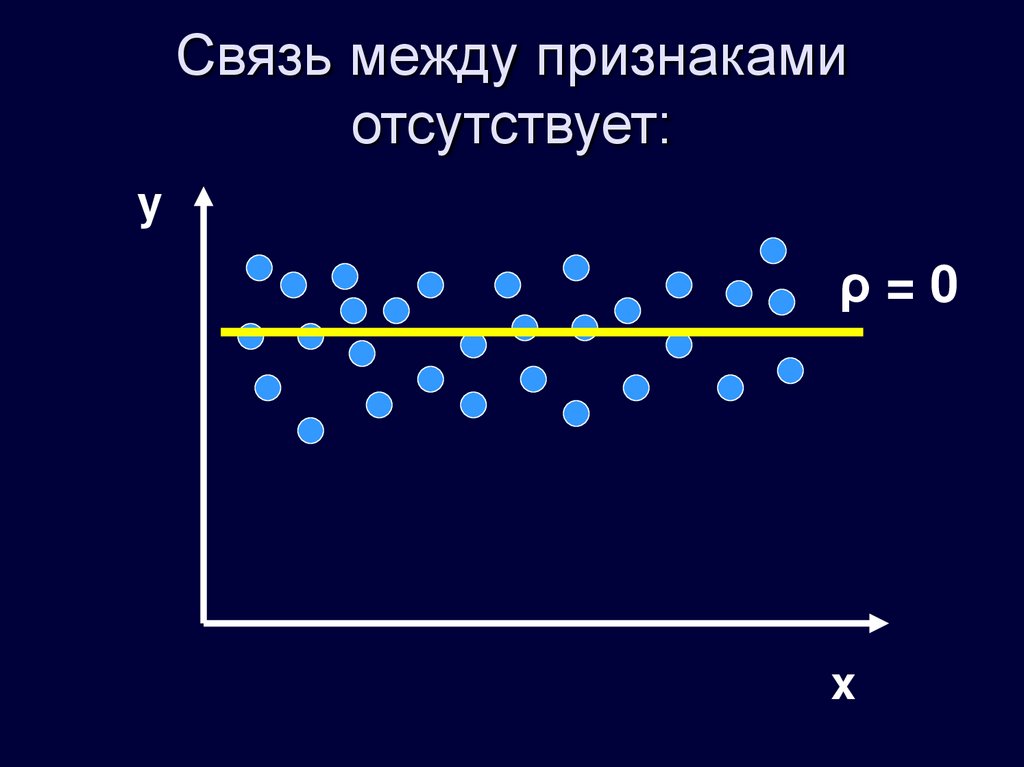
16. Связь между признаками отсутствует:
yρ=0
x
17. Случайная выборка может показать наличие связи:
yH0 : ρ = 0
x
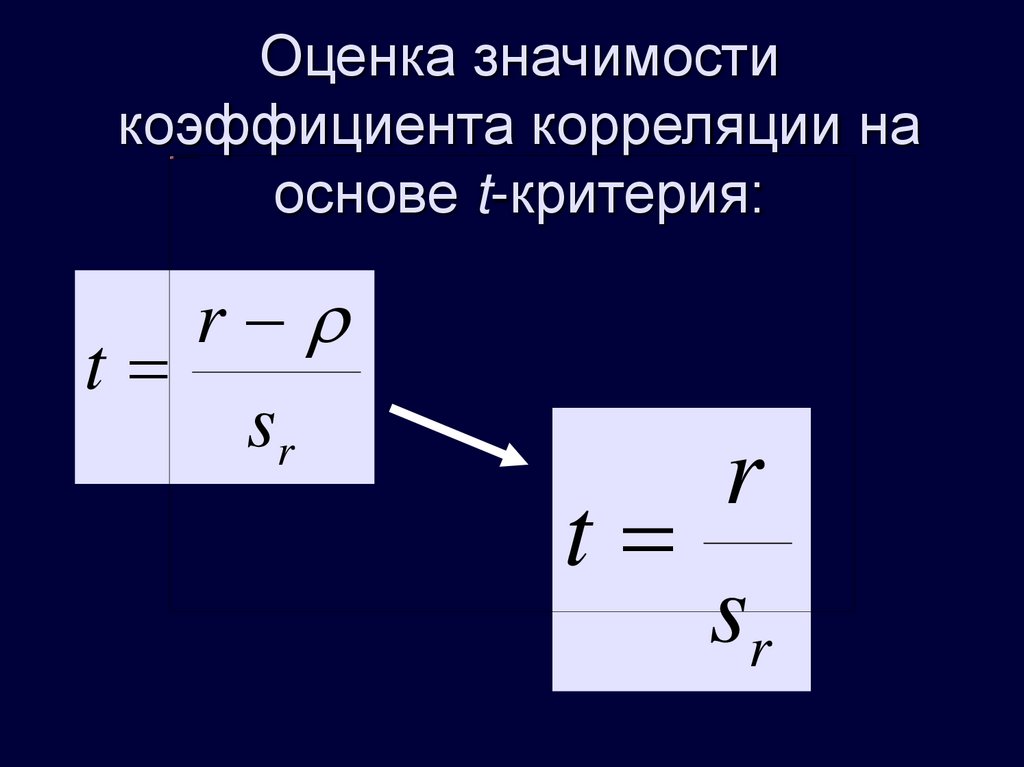
18. Оценка значимости коэффициента корреляции на основе t-критерия:
rt
sr
r
t
sr
19. Подставляем формулу для вычисления sr:
n 2r n
t
r
t
2
2
1 r
1 r
n > 100
n < 100
20. Интерпретация t-теста:
При t > tα → НАdf = n – 2
21. 9.4. z-преобразование Фишера
22. z-преобразование коэффициента корреляции по Фишеру:
1 1 rz ln
2 1 r
1 r
z 1,15129 lg
1 r
23. Пределы колебаний величины z:
z ( ; )распределение близко к нормальному
24. Оценка значимости z по t-критерию:
ztz z n 3
sz
25. z-преобразование по Фишеру:
этот критерий пригоден для выборкилюбого объема!
позволяет с большей уверенностью
оценивать значимость r, а также
разность r1-r2
26. 9.5. Минимальное число наблюдений для планируемой точности коэффициента корреляции
27. Необходимый объем выборки для заданной точности коэффициента корреляции:
2t
n 2 3
z
28. Пример:
n = 14, r = 0,428 z = 0,523tz = 0.523√(14-3) = 1.73
1.73 < 2.18 (α = 0.05, df = 12)
Н0
2
(2.58)
6.656
n
3
3 24 3 27
2
(0.523)
0.274
29. 9.6. Сравнение двух коэффициентов корреляции
30. Оценка значимости разницы между коэффициентами корреляции:
tr1 r2
s s
2
r1
t
2
r2
z1 z2
1
1
n1 3 n2 3
для малых
выборок
31. 9.7. Коэффициент корреляции Спирмена
32. Ранговый коэффициент корреляции Спирмена (Spearman):
6 drs 1
2
n(n 1)
2
d – разность между рангами
сопряженных значений
признаков X и Y
33.
XY
ранг X
ранг Y
d2
1.3
1.8
2.4
3.4
4.8
…
6.3
54.8
300
1335
250
946
670
1
2
3
4
5
2
12
1
8
7
1
100
4
16
4
380
1700
7
20
3
17
16
9
364
6 * 364
rs 1 3
0.73
20 20
34. 9.8. Корреляция между качественными признаками
35. Коэффициент ассоциации:
ad bc(a b)(c d )( a c)(b d )
пределы изменений:
от -1 до +1
36. Оценка значимости коэффициента ассоциации:
n2
2
df = (2-1)(2-1) = 1

































 Математика
Математика








