Похожие презентации:
Корреляционный анализ
1. Корреляционный анализ
Основные задачи1) Существует ли связь между факторами и
откликом?
2) Оценить силу связи
3) Выявить факторы, оказывающие
наибольшее влияние на отклик
Основное числовые характеристики
1) Выборочный коэффициент корреляции
Пирсона
2) Ранговые коэффициенты корреляции
3) Выборочное корреляционное отношение
4) Множественный и частный коэффициенты
корреляции
1
2. Шкалы измерений
Количественные признаки1) Абсолютная шкала (начало отсчета+единицы
измерения)
2) Шкала отношений (во сколько раз)
3) Интервальная шкала (на сколько единиц)
Качественные признаки
1) Порядковая шкала (ординальная)
2) Номинальная (шкала наименований)
2
3. Коэффициент корреляции Пирсона
ТВrxy
cov X , Y
X Y
~r
xy
1) X , Y независимы
rxy 0
2)
rxy 1
3) Y
a bX
r 1
xy
МС
x
x
y
y
i i
2
2
xi x yi y
Для 2НГС оценка
асимптотически
несмещенная,
асимптотически
эффективная
1
~
rxy n
x y x y
i
i
s X sY
3
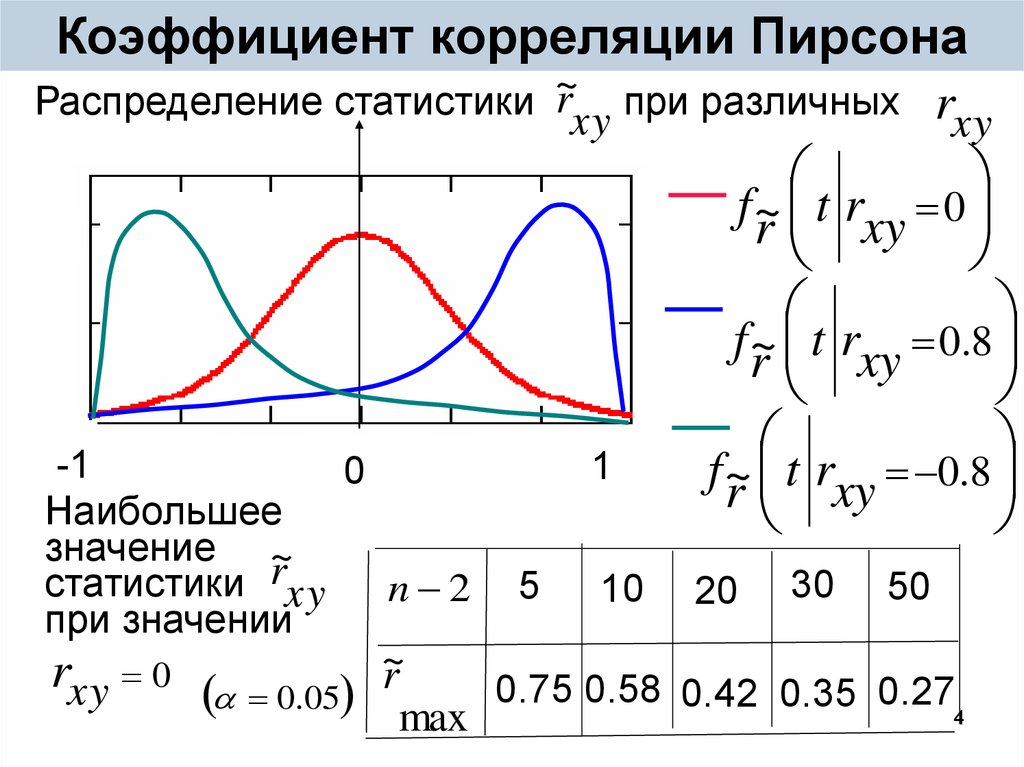
4. Коэффициент корреляции Пирсона
r при различных rРаспределение статистики ~
xy
xy
-1
0
Наибольшее
значение ~
статистики rxy
n 2
при значении
rxy 0 0.05 ~r
max
1
5
10
f~
r t rxy 0
f~
t
r
0
.
8
r xy
f~
t
r
0.8
xy
r
20
30
50
0.75 0.58 0.42 0.35 0.27
4
5. Коэффициент корреляции Пирсона
Задача 1 (о значимости связи)(2НГС+некоррелированность)≡(независимость)
Гипотеза
H o : rxy 0
Требования
2 НГС ,
Оценки
x , y , s , s ,~
r
x y xy
Статистика
Распределение
~
rx y
n 50
n 2
1 ~
rx2
y
T n 2
5
6. Коэффициент корреляции Пирсона
Задача 1 (о значимости)(2НГС+некоррелированность)≡(независимость)
n 66, ~
r 0.4
Пример.
xy
Г H o : rxy 0
H : r
Т
2НГС , n 50
О
x , y , s , s ,~
r
x y xy
С
Р
~
rxy n 2
2
1 ~
rxy
1)
0,05
0
o
xy
H1 : r
0
xy
2) tтабл t 0.025 ; 60 2.0
3) tнабл
0, 4 8
1 0,16
3,6
4) tнабл tтабл H1
T n 2
6
7. Коэффициент корреляции Спирмена
а) ГС не является нормальнойб) X,Y – в порядковой шкале
в) n<50
1
~
rxy n
x y x y
i i
sx sy
di xi yi
xi xi
n n
H o : rys
0 y
i
i
1) X , Y независимы rs 0 H1 : rs 0
2
6 di
rs 1
3
2)
rs 1
3) X , Y монотонная связь
rs 1
H0: связь незначима
Н1: связь значима
rs n 2
1 rs2
~ T n 2
7
8. Коэффициент корреляции Спирмена
Пример. Y – вес монеты (грамм), X- возраст (лет)xi
5
9
14
17
23
31
35
42
46
50
yi 2.82 2.85 2.80 2.80 2.79 2.78 2.77 2.79 2.75 2.72
xi
yi
di
di
1
2
9 10
-8 -8
xi yi
3
4
5
6
7
8
9
10
7.5
-4.5
7.5
5.5
4
3
5.5
2
1
-3.5 -0.5
2
4
2.5
7
9
2
di 317
rs 0.92
2
6 di
rs 1
3
n n
8
9. Коэффициент корреляции Спирмена
Пример. Y – вес монеты (грамм), X- возраст (лет)xi
5
9
14
17
23
31
35
42
46
50
yi 2.82 2.85 2.80 2.80 2.79 2.78 2.77 2.79 2.75 2.72
1 между
2
3 возрастом
4
5 и весом
6
7монеты
8
xi
Вывод:
значимая
(обратная)
yi 9 10 монотонная
3
5.5
4
7.5 7.5 связь
5.5
di
-8
-8
-4.5
-3.5 -0.5
H0: связь незначима
Н1: связь значима
0.92 8
tнабл
6.17
1 0,85
tтабл t 0.025 ; 8 2.31
2
4
2.5
9
10
2
1
7
9
rs 0.92
rs n 2
1 rs2
~ T n 2
9
10.
Корреляционное отношениеПример. Корреляционная таблица 1
3
5
7
nx
yx
2
8
4
0
12
3.67
4
6
0
3
9
4.33
6
4
3
2
9
4.56
ny
18
7
5
n 30
X
Y
2
sмежгр
2
~
yx 2
sобщ
y 4.13
1
2
2
sмежгр nx y x y
n
1
2
2
sобщ n y y y
n
10
11. Корреляционное отношение
ТВ2
yx
2
y x
2
y
МС
2
sмежгр
~
yx
2
sобщ
2
sмежгр
2
~
yx 2
sобщ
Свойства корреляционного отношения
2
2
1) yx xy
4) yx 0 Y , Х независимы
2) 0 yx 1
5)
1
связь
yx
yx ryx
6)
r
связь
yx yx
3)
функционал ьная
линейная
11
12. Корреляционное отношение
Пример. Корреляционная таблица 2X
Y
2
4
6
ny
3
6
0
0
6
5
3
5
5
13
7
0
2
9
11
nx
yx
9
7
14
n 30
3.67
5.57
6.29
y 5.18
2
sобщ
2
sмежгр
2
yx
2
ryx
Пример 1
2.32
0.15
0.066
0.061
Пример 2
2.18
1.29
0.594
0.588
12
13. Корреляционное отношение
Задача 2. Проверка линейностиГипотеза
Требования
Оценки
Статистика
H o : yx r yx
2НГС ,
n 50
ryx , yx
r n r
1 r 2
2
2
yx
yx
2
yx
Распределение
F r 2, n r
13
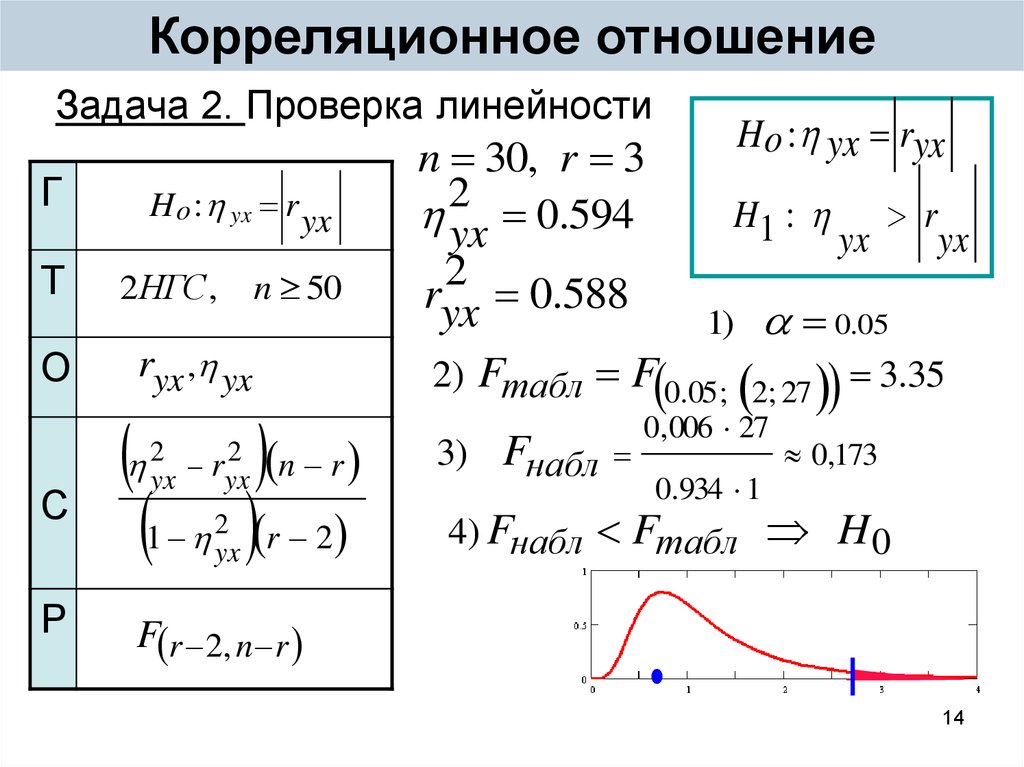
14. Корреляционное отношение
Задача 2. Проверка линейностиГ
Т
О
С
Р
H o : yx r yx
2НГС ,
n 50
ryx , yx
r n r
1 r 2
2
2
yx
yx
2
yx
H o : yx ryx
n 30, r 3
2
H1 : r
yx 0.594
yx
yx
2
ryx 0.588
1) 0.05
2) Fтабл F 0.05; 2; 27 3.35
3) Fнабл
0,006 27
0.934 1
0,173
4) Fнабл Fтабл H 0
F r 2, n r
14
15. Многомерный корреляционный анализ
r11 r12 ... r1 pX1, X 2 , ..., X p
1) Парные коэффициенты
r21 r22 ... r2 p
корреляции
Q
...
... ... ...
2) Множественный
коэффициент корреляции r p1 r p 2 ... r pp
Q
Ri, 1,..., i 1,i 1,..., p 1
0 R 1
Qii
2
алгебраическое
R n p
Qii дополнение к r
ii
~ F p 1; n p
2
3) Частные коэффициенты
корреляции
1 rij , 1... p 1
1 R p 1
rij , 1,..., p
Qij
Qii Q jj
15
16. Многомерный корреляционный анализ
r11
1) Парные коэффициенты
Q r21
корреляции
r
2) Множественный
31
X 1, X 2 , X 3
коэффициент корреляции
r12
r22
r32
r13
r23
r33
2
2
r13 2r12r13r23 r23
R3, 1,2
2
1 r12
0 R3, 1,2 1
3) Частные коэффициенты
корреляции
r13 2
r13 r12r32
2
2
1 r12 1 r32
1 r13, 2 161
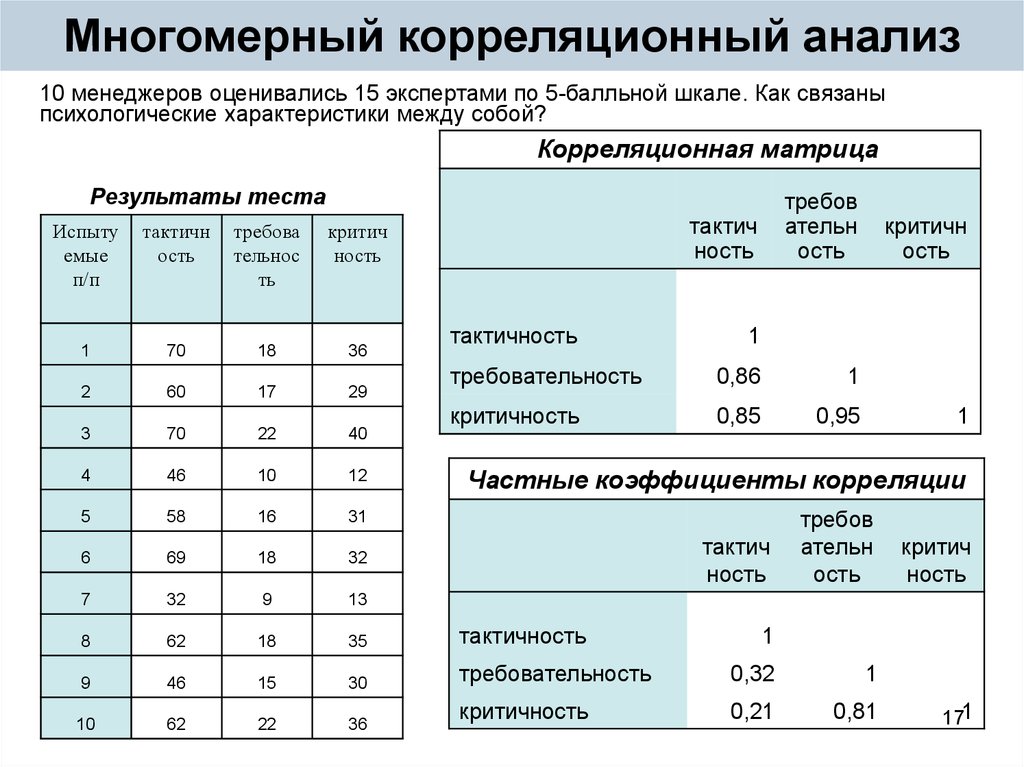
17. Многомерный корреляционный анализ
10 менеджеров оценивались 15 экспертами по 5-балльной шкале. Как связаныпсихологические характеристики между собой?
Корреляционная матрица
Результаты теста
требов
ательн
ость
тактич
ность
критичн
ость
Испыту
емые
п/п
тактичн
ость
требова
тельнос
ть
критич
ность
1
70
18
36
2
60
17
29
3
70
22
40
4
46
10
12
5
58
16
31
6
69
18
32
7
32
9
13
8
62
18
35
тактичность
9
46
15
30
требовательность
0,32
1
10
62
22
36
критичность
0,21
0,81
тактичность
1
требовательность
0,86
1
критичность
0,85
0,95
1
Частные коэффициенты корреляции
тактич
ность
требов
ательн
ость
критич
ность
1
171














 Математика
Математика








