Похожие презентации:
Основы теории вероятностей и математической статистики. Лекция 11
1.
ПРАКТИЧЕСКАЯ ФИЗИКАДоцент кафедры
экспериментальной физики
Ерина Марина Васильевна
2.
Лекция № 11Основы теории вероятностей и математической
статистики
• Предельные распределения.
• Основы теории вероятностей. Теоремы теории
вероятностей.
• Распределение Бернулли
3.
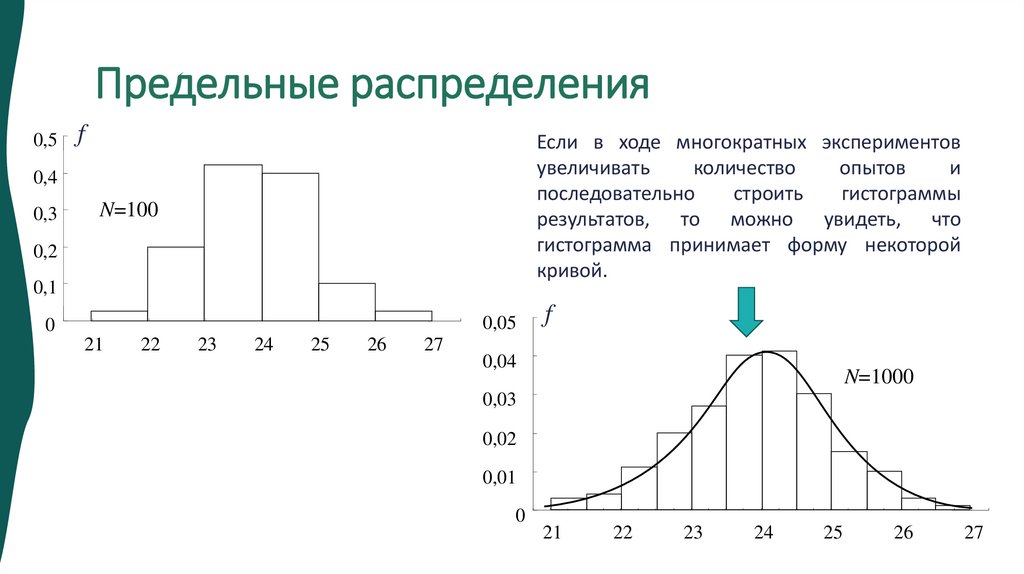
Предельные распределения0,5
f
Если в ходе многократных экспериментов
увеличивать
количество
опытов
и
последовательно
строить
гистограммы
результатов, то можно увидеть, что
гистограмма принимает форму некоторой
кривой.
0,4
0,3
N=100
0,2
0,1
0,05
0
21
22
23
24
25
26
27
f
0,04
N=1000
0,03
0,02
0,01
0
21
22
23
24
25
26
27
4.
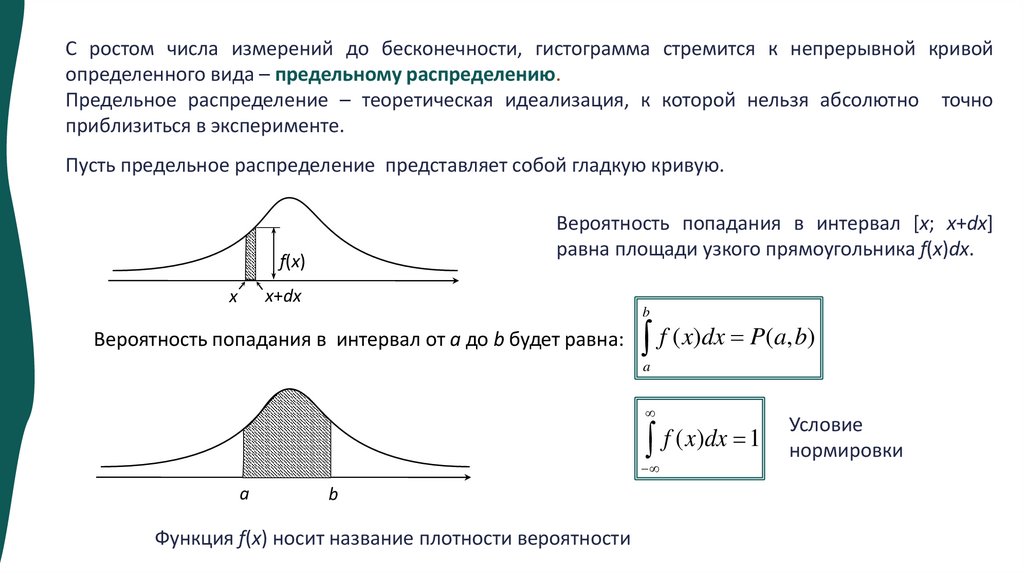
С ростом числа измерений до бесконечности, гистограмма стремится к непрерывной кривойопределенного вида – предельному распределению.
Предельное распределение – теоретическая идеализация, к которой нельзя абсолютно точно
приблизиться в эксперименте.
Пусть предельное распределение представляет собой гладкую кривую.
Вероятность попадания в интервал [x; x+dx]
равна площади узкого прямоугольника f(x)dx.
f(x)
x+dx
x
b
Вероятность попадания в интервал от a до b будет равна:
f ( x)dx P(a, b)
a
f ( x)dx 1
a
b
Функция f(x) носит название плотности вероятности
Условие
нормировки
5.
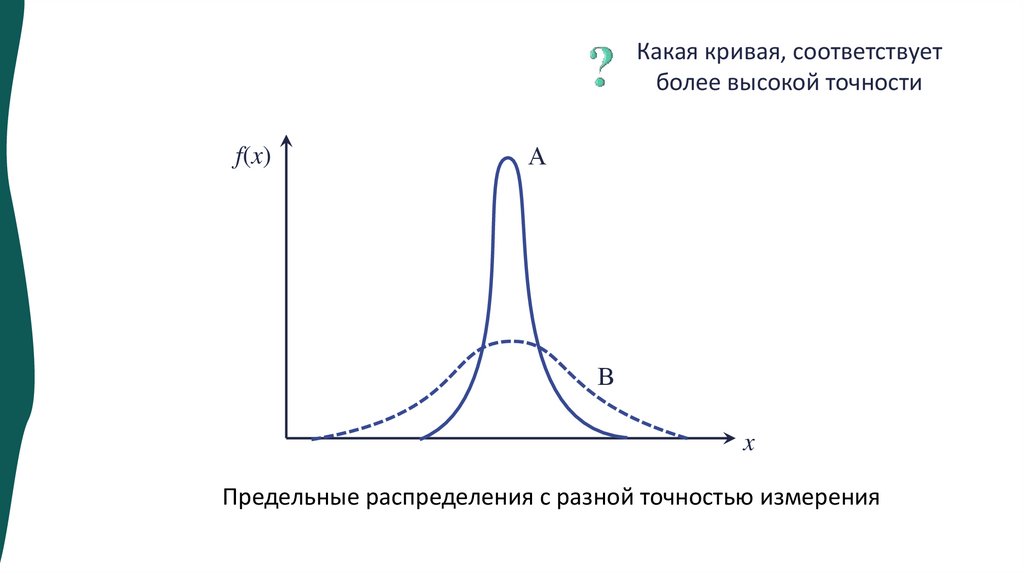
Какая кривая, соответствуетболее высокой точности
f(x)
А
В
x
Предельные распределения с разной точностью измерения
6.
f(x)Высокая
точность
Низкая
точность
x
Предельные распределения с разной точностью измерения
7.
Основы теории вероятностейТеория вероятностей – математическая наука, изучающая
закономерности в случайных явлениях
Под событием в теории вероятностей понимается всякий факт, который в
результате опыта может произойти или не произойти.
8.
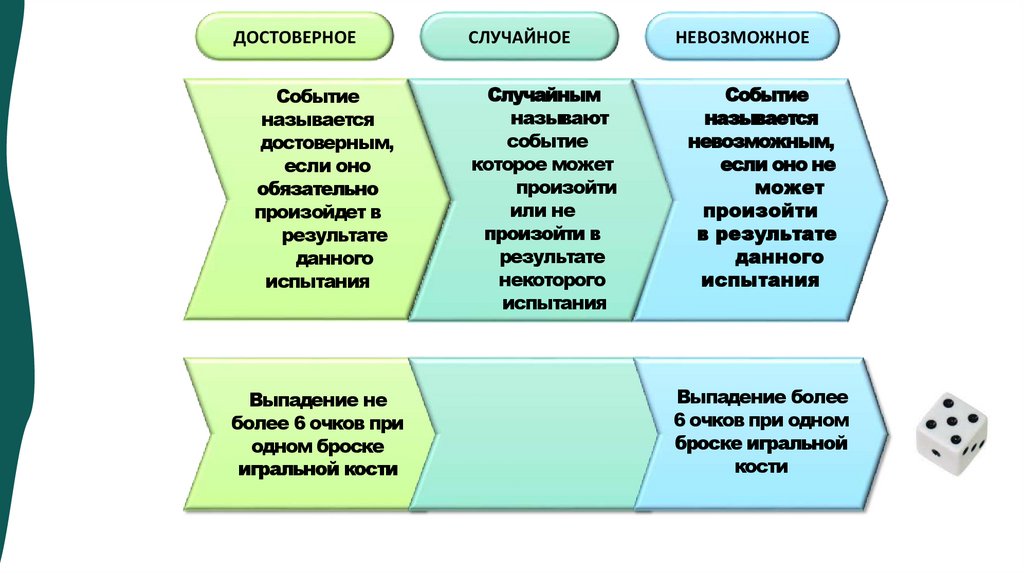
ДОСТОВЕРНОЕСобытие
называется
достоверным,
если оно
обязательно
произойдет в
результате
данного
испытания
Выпадение не
более 6 очков при
одном броске
игральной кости
СЛУЧАЙНОЕ
НЕВОЗМОЖНОЕ
Случайным
называют
событие
которое может
произойти
или не
произойти в
результате
некоторого
испытания
Событие
называется
невозможным,
если оно не
может
произойти
в результате
данного
испытания
Выпадение более
6 очков при одном
броске игральной
кости
9.
Несколько событий в данном опыте образуют полную группу событий, если врезультате опыта непременно должно произойти одно из них.
Например: выпадение герба или цифры при одном броске монеты.
Совместными называются события, если появление одного из них не
исключает появления другого в одном и том же испытании.
Например: два стрелка стреляют по мишени.
Несколько событий называются несовместными в
данном опыте, если никакие два из них не могут
проявиться вместе.
Например: попадание и промах при выстреле.
10.
Статистической частотой события А называется отношение числа опытов, вкоторых появилось это событие, к общему числу опытов:
F ( A)
Вероятностью события А называется
k
n
k
P( A) lim F ( A) lim
n
n n
Очевидно, что вероятность достоверного события равна 1, а вероятность
невозможного равна 0.
11.
Теоремы теории вероятностейСуммой нескольких событий называется событие, состоящее в появлении хотя
бы одного из этих событий.
Произведением нескольких событий называется событие, состоящее в
совместном появлении всех этих событий.
Например: из колоды, содержащей 36 карт,
вытаскивают одну: первое событие – появление
короля, второе – появление карты пиковой масти.
Сумма этих событий будет либо появление короля
любой масти, либо появление любой пиковой карты.
Произведение этих же событий – появление короля
пик.
12.
Теорема сложения вероятностей:Вероятность суммы двух несовместимых событий равна сумме вероятностей этих
событий:
P( A B) P( A) P( B)
Например: игральную кость бросают один раз.
Необходимо определить вероятность выпадения
нечетной цифры, т.е. 1, 3 и 5.
Если события совместны, то
Для примера с пиковым королем:
1 1 1 1
6 6 6 2
P( A B) P( A) P( B) P( AB)
или
1 1 1
1











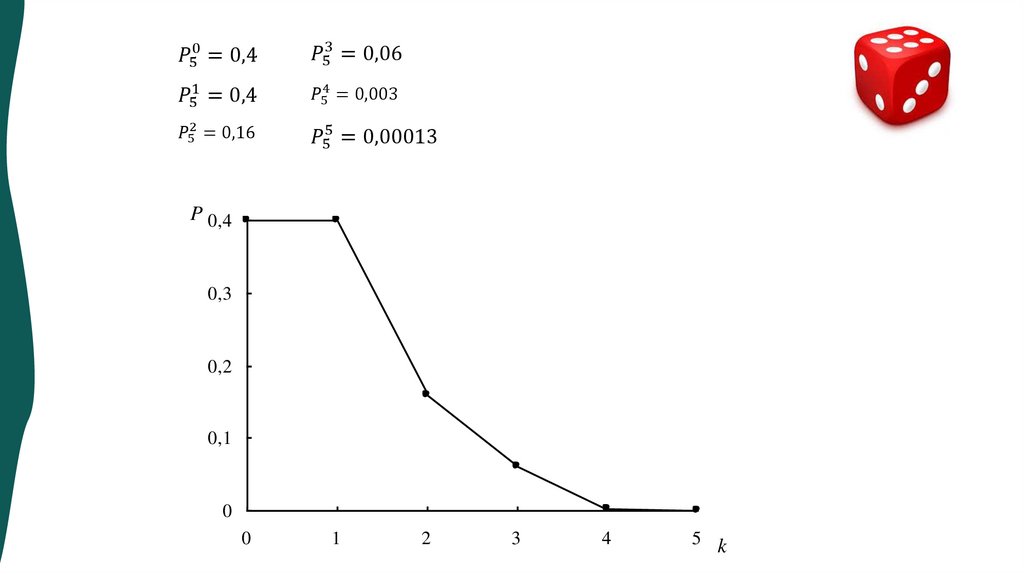

 Математика
Математика








