Похожие презентации:
Теоретические основы цифровой обработки сигналов
1. Теоретические основы цифровой обработки сигналов
Новгородский государственный университет имени Ярослава МудрогоНаучно-исследовательская лаборатория цифровой обработки сигналов
Теоретические основы
цифровой обработки сигналов
Иллюстративный материал к конспекту лекций
Великий Новгород 2004
2. Литература
1.2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
Рабинер Л., Гоулд Б.. Теория и применение цифровой обработки сигналов.
/пер. с англ. – Мир, 1978
Солонина А.И.,Улахович Д.Л. и др. Основы ЦОС. Курс лекций. Изд.2-е СПб.:Питер,2005
А.Б.Сергиенко. Цифровая обработка сигналов. – СПб.: Питер, 2003 г.
Куприянов М.С., Матюшкин Б.Д. Цифровая обработка сигналов.– СПб.:
Политехника,1998
Гольденберг Л.М. и др. Цифровая обработка сигналов. Справочник. – М.:
Радио и связь, 1985
Айфичер Э.С, Джервис Б.У. Цифровая обработка сигналов: практический
подход, 2-е издание .Пер. с англ. – М.: Издательский дом «Вильямс», 2004
Лайонс Р. Цифровая обработка сигналов. пер. с англ. под ред. Бритова А.А.
– М.: Бином, 2006.
Применение цифровой обработки сигналов под ред. Оппенгейма. – М.: Мир,
1980
Введение в цифровую фильтрацию. Под ред. Богнера Г. Пер. с англ. – М.:
Мир, 1976
Каппелини В., Константиниос А.Д., Эмилиини П., Цифровые фильтры и их
применение. – М.: Энергоавтомиздат, 1983
Блейхут Р. Быстрые алгоритмы цифровой обработки сигналов, М., Мир,
1989
Гольденберг К.Н., Матюшкин Б.Ю., Поляк Н.Н., Цифровая обработка
сигналов. – М.: Радио и связь, 1990
Карташев В. Г. Основы теории дискретных сигналов и цифровых фильтров.
– М.: Высшая школа, 1982
Теоретические основы цифровой обработки сигналов. Слайд 2
3. Основные области применения ЦОС
СвязьКодирование речи
Военная техника
Распознавание речи
Спектральный
анализ
Синтезаторы
музыки
Верификация
диктора
Компенсаторы
эхо
Ультразвуковое
Засекреченная
оборудование
связь
Генерация
функций
Игрушки
и игры
Повышение
качествафильтрация
речи
Цифровая
Видео-конференц.
связь
Обработка
Диагностический
Радиолокация
инструментарий
Анализ
сейсмограмм
Робототехника
Цифровое
вещание
и телевидение
Общетехнические
Синтез
речи
Свертка
Модемы
изображений
Мониторинг
Обработка
больных
изображений
Цифровая
фильтрация
Цифровое
управление
……………………………………………..
Системы
“речь - текст”
Корреляция
Космическая
фотосъемка
Зрение
роботов
Цифровое
радио
Слуховые
Навигация
приборы
Синтез
моделей доступ
Засекреченный
Преобразование
Гильберта
Компрессия
данных
Компрессия
и
передача
Трансмультиплексоры
Протезирование
Радиомодемы
Временной
анализ
Контрольная
аппаратура для ЛЭП
изображений
Быстрое преобразование
Фурье
Анализ
измерений
космических
зондов
Сотовая
телефония
Управление
ракетами
Анализ
вибраций
Медицина
ОбработкаРадиотелескопы
речи
Распознавание
образов
Адаптивная
фильтрация
Интеллектуальные
мультиплексоры
Радиоразведка
Фазовая синхронизация
Повышение
качества
изображения
Генерация
сигналов
Адаптивные
корректоры
Гидроакустика
Трехмерные
вращения
Кодирование
- декодирование
Интерполяция
картами
ШифрованиеРабота
данныхс цифровыми
Космонавтика
Инструментарий
Пакетная коммутация
Другие
Широкополосная связь
Промышленность
ЦОС
Теоретические основы цифровой обработки сигналов. Слайд 3
4. Основные области применения ЦОС
Взаимодействие ЦОС с другимиобластями науки и техники
Обработка
аналоговых
сигналов
цос
Теория
вероятности
и статистика
Теоретические основы цифровой обработки сигналов. Слайд 5
5. Взаимодействие ЦОС с другими областями науки и техники
Основные теоретические направления ЦОСЦифровая обработка сигналов
Цифровая
фильтрация
Спектральный
анализ
Многомерная
обработка
КИХ-фильтры
Фильтрация
Томография
БИХ-фильтры
БПФ
Повышение качества
Лестничные
Оценка СПМ
Снижение
избыточности
Адаптивные
Классическая
Дифференц.
модуляция
Параметрическая
Ортогональное
преобразование
Теоретические основы цифровой обработки сигналов. Слайд 6
6. Основные теоретические направления ЦОС
Элементная база ЦОСЭлементная база ЦОС
Цифровые ИС
МИС
СИС
Дискретноаналоговые ИС
АЦП
Универсальные
ЦВМ
Специализ.
ЦВМ
МикроЭВМ
Сигнальные
процессоры
БИС
СБИС
ЦАП
ПЭВМ
Сигнальные
сопроцессоры
ПЛИС
БМК
ПЗС-ППЗ
Большие
ЭВМ
Спец.
процессоры
Програм.
Репрогр.
УКК
Супер ЭВМ
Транспьютеры
Теоретические основы цифровой обработки сигналов. Слайд 7
7. Элементная база ЦОС
Примеры устройств ЦОСТеоретические основы цифровой обработки сигналов. Слайд 8
8. Примеры устройств ЦОС
Теоретические основы цифровой обработки сигналов. Слайд 99. Примеры устройств ЦОС
Средства разработки системы ЦОСАссемблер
MOV A,B
11010100010001
Языки высокого уровня
(C, C++, VHDL, Abel, Verilog,
HDL,….)
САПР
Отладочный
комплект
(EZ-Kit)
Эмулятор
Система ЦОС
Теоретические основы цифровой обработки сигналов. Слайд 10
10. Средства разработки системы ЦОС
Пример аналогового и цифрового устройствАналоговое устройство
+
Цифровое устройство
ФНЧ
ЦАП
АЦП
1010
1001
Теоретические основы цифровой обработки сигналов. Слайд 11
11. Пример аналогового и цифрового устройств
Сравнительная характеристика цифровой ианалоговой обработки
Преимущества
•Повторяемость
(малочувствительны к старению, к
допускам точности компонентов, к
изменениям температуры)
•Высокая помехоустойчивость
•Большой динамический
диапазон
•Высокая точность
•Универсальность методов и
аппаратуры
•Гибкость (Возможность
программной перестройки)
Недостатки
•Большие требования к
быстродействию (ширине полосы
частот)
•Сложность методов и
аппаратуры
•Большая мощность
потребления энергии
•Наличие погрешностей
дискретизации и шумов
квантования
•Высокая скорость морального
старения
•Высокая степень интеграции
Теоретические основы цифровой обработки сигналов. Слайд 12
12. Сравнительная характеристика цифровой и аналоговой обработки
Раздел 1. Теория дискретных системНепрерывные, дискретные и цифровые сигналы
Представление сигналов
Графически
y(t) В, y(n), ý(n)
1000, 8
0111, 7
0110, 6
Цифровой сигнал (квантование по
уровню и дискретизация по времени)
Непрерывный (аналоговый) сигнал
Дискретный сигнал
(дискретизация по времени)
q
1.
0011, 3
0010, 2
0001, 1
T
0.1
0.2
0.5
0.6
0.7
0.8
0.9 t, сек
1
2
5
6
7
8
9
n
T=1/fd – шаг дискретизации, fd- частота дискретизации, q –шаг квантования
0
Теоретические основы цифровой обработки сигналов. Слайд 13
13. Раздел 1. Теория дискретных систем
Непрерывные, дискретные и цифровые сигналы2.
3.
Набор чисел: 0, 0.5, 0.25, 0.125..
Аналитически: x(n)=1/2n, n=0, 1, 2..
4.
Рекуррентно: x(n)=x(n-1)/2, x(0)=1, n=0, 1, 2..
Примеры последовательностей:
u0(n)
1
-2 -1 0 1
u-1(n-nu0)-1(n)
u0(n-n0)
1
2
n
единичный импульс
1
0
n0
n
единичный импульс,
задержанный на n0 отсчетов
1
0
0n0
единичный
единичный скачок
скачок
задержанный на n0
отсчетов
если задана a(n), n , то
a (n) a (m)u0 (n m)
m
Теоретические основы цифровой обработки сигналов. Слайд 14
n
14.
Линейные системы с постоянными параметрами (ЛПП)x(n)
Ф[x(n)]
y(n)
Дискретная ЛПП
Свойства ЛПП
Линейность
Если
x1(n)
и
Ф
x2(n)
Ф
то
a1x1(n) +a2x2(n)
Ф
Инвариантность задержки
y1(n)
y2(n)
a1y1(n) +a2y2(n)
Если
x(n)
то
x(n-n0)
Ф
Ф
n0
Теоретические основы цифровой обработки сигналов. Слайд 15
y(n)
y(n-n0)
n0
15. Линейные системы с постоянными параметрами (ЛПП)
Свойства ЛППКоммутативность (перестановка):
Если
x(n)
Ф1
Ф2
y(n)
то
x(n)
Ф2
Ф1
y(n)
Теоретические основы цифровой обработки сигналов. Слайд 16
16. Свойства ЛПП
Суперпозицияx1(n)
+
Синтез
x2(n)
x (n)
Разложение
+
x3(n)
Теоретические основы цифровой обработки сигналов. Слайд 17
17. Суперпозиция
Импульсная характеристикаh(n) – импульсная характеристика – отклик системы
на единичный импульс u0(n)
u0(n)
Дискретная
ЛПП
h(n)
Характеристики ЛПП полностью определяются ее
импульсной характеристикой
Теоретические основы цифровой обработки сигналов. Слайд 18
18. Импульсная характеристика
Фундаментальная концепция ЦОСx(n)
y(n)
h(n)
разложение
(декомпозиция)
синтез
y(n)=y1(n)+y2(n)+y3(n
)
x(n)=x1(n)+x2(n)+x3(n)
y1(n)
x1(n)
h(n)
+
+
x2(n)
y2(n)
h(n)
x3(n)
+
y3(n)
+
h(n)
Теоретические основы цифровой обработки сигналов. Слайд 19
19. Фундаментальная концепция ЦОС
Сверткаm
m
y n x n h n x m h n m x m n h m ,
h( ) – импульсная характеристика, – оператор свертки.
где
h(n), x(m)
h(n), x(m)
2
1
2
1
-4 -3 -2 -1 0 1 2 3 4 5 6 7 8
-4 -3 -2 -1 0 1 2 3 4 5 6 7 8
h(n-m), x(m)
h(n-m), x(m)
0 0 0 00 1
01 0
20
0 00 00 00 000 000
2 003300404
0 0 0 00 2
02 0
20
2 002200202
0 00 00 00 000 00
nn == -1
7
6
5
4
3
2
1
0
nn == -1
7
6
5
4
3
2
1
0
-4 -3 -2 -1 0 1 2 3 4 5 6 7 8
y(n)
8
-4 -3 -2 -1 0 1 2 3 4 5 6 7 8
y(n) 9
6
3
-4 -3 -2 -1 0 1 2 3 4 5 6 7 8
-4 -3 -2 -1 0 1 2 3 4 5 6 7 8
Теоретические основы цифровой обработки сигналов. Слайд 20
20. Свертка
Физическая реализуемость ЛППЕсли h(n)=0 при n<0
h(n)
h(n)
0
нереализуемая
0
реализуемая
Условие устойчивости ЛПП
h n
n
y1(n),
y2(n),
y3(n) 1
0.25n
y1(n)=0.1 2
u-1(n) - не устойчивая
n
-2
0
2
4
6
8
10
12
14
y2(n)=0.8 u-1(n)
- устойчивая
y3(n)=1/n u-1(n)
-?
n
Теоретические основы цифровой обработки сигналов. Слайд 21
21. Физическая реализуемость ЛПП
Разностные уравненияНазначение:
• временной анализ дискретных систем;
• способ построения системы;
• порядок, нули, собственные частоты.
Разностное уравнение М-го порядка:
M
M
i 0
i 1
y n bi x n i ai y n i , n 0, aM 0
Пример ЛПП 2-го порядка
y n b0 x(n) b1 x(n 1) b2 x(n 2) a1 y(n 1) a2 y(n 2)
x(n-2)
x(n-1)
b2
b1
x(n)
b0
y(n)
+
-a1
-a2
y(n-1)
y(n-2)
Теоретические основы цифровой обработки сигналов. Слайд 22
22. Разностные уравнения
Частотная характеристика ЛПППусть x(n)=ej n – дискретный комплексный гармонический сигнал.
Тогда при прохождении его через ЛПП с ИХ h(n)
y(n) h(m) e j ( n m ) e j n h(m) e j m
m
x(n)
m
H ( e j )
Частотная характеристика ЛПП:
H (e j ) H (e j 2 k ) h(n) e j n , k 0, 1, 2,
n
Теоретические основы цифровой обработки сигналов. Слайд 23
23. Частотная характеристика ЛПП
Преобразование Фурье для дискретных сигналовДля непрерывных сигналов:
X н ( j ) xн (t ) e
j t
dt
Для дискретных сигналов:
X (e ) x(n) e j n
j
1
1
j
j n
j t
x
(
n
)
X
(
e
)
e
d
xн (t )
X
(
j
)
e
d
н
2
2
т.к. X(ej )=X(ej +2 k), k=0, 1, 2…
X(ej ) непрерывная и
периодичная (период 2 )
Теоретические основы цифровой обработки сигналов. Слайд 24
24. Преобразование Фурье для дискретных сигналов
Свойства ПФ для дискретных сигналовПоследовательность
x(n) y(n)
Преобразование Фурье
X(ej ) Y(ej )
1. Линейность
a x(n)+b y(n)
a X(e )+ b Y(e )
2. Задержка
x(n-n0)
ej n0 X(ej )
3. Частотный сдвиг
ej 0n x(n)
X(ej( - 0))
4. Свертка
x(n) y(n)
X(ej ) Y(ej )
x(n) y(n)
1
j
j ( )
X
(
e
)
Y
(
e
) d
2
Свойство
5. Произведение
j
Теоретические основы цифровой обработки сигналов. Слайд 25
j
25. Свойства ПФ для дискретных сигналов
Соотношение между ПФ дискретных и непрерывных сигналов|Xн(j )|, |X(ej T)|
/T 2 /T- 0 2 /T 0+2 /T 3 /T
fд/2
fд
3fд/2
0 0
- /T
-fд/2
Re[xн(t)]=xн(t)
X e
j T
4 /T
2fд
1
2
T x’ T m
m
x(n, 0) , x(n, 0+2 /T), x(n, 2 /T- 0), x(nT, 0)
1
0.5
t
0
T
2T
3T
-0.5
-1
Теоретические основы цифровой обработки сигналов. Слайд 26
4T
26. Соотношение между ПФ дискретных и непрерывных сигналов
Эффект наложения спектров (aliasing)max= д – без наложения
|Xн(j )|, |X(ej T)|
0
д/2
д
3 д/2
2 д
5 д/2
6 д
max > д – наложения
|Xн(j )|, |X(ej T)|
ФНЧ
0
д/2
д
д/2
2 д
5 д/2
6 д
max = д – без наложения
|Xн(j )|, |X(ej T)|
0
3 д/2
д
3 д/2
2 д
5 д/2
Теоретические основы цифровой обработки сигналов. Слайд 27
6 д
27. Эффект наложения спектров (aliasing)
Z-преобразованиеПрименяется для описания, синтеза и анализа ЛПП
Преобразование Лапласа
Z-преобразование
X ( , ) x(n) e n e j n
X ( s) x(t ) e dt
st
n
e n r n , ln(r )
s j
X ( , ) x(t ) e
t
e
j t
dt
X (r , ) x(n) r n e j n
n
X ( z ) x(n) z n , z re j
n
Теоретические основы цифровой обработки сигналов. Слайд 28
28. Z-преобразование
Z-плоскостьX ( z ) x(n) z n , z re j , r-радиус, -угол, ej - единичная окружность
n
Im(Z)
1
0
1
ЛПП устойчива, если все
полюса находятся внутри
единичной окружности:
rp<1
Re(Z)
Для любой ЛПП X(z) можно представить в виде:
1 z z
M
X z A
i 1
N
i
1 pi z 1
i 1
M
1
a z
i
где
i
i 0
N
1 bi z i
,
zi – нули;
pi – полюса.
i 1
Теоретические основы цифровой обработки сигналов. Слайд 29
29. Z-плоскость
Примеры Z-преобразованияx(n)
Z[x(n)]
x(n)
Z[x(n)]
u0(n)
1
ej n
1/(1-ej z-1)
u-1(n)
1/(1-z-1)
nan-1
z-1/(1-az-1)2
(-1)n
1/(1+z-1)
n
z-1/(1+z-1)2
ansin(n )
az 1 sin
1 2az 1 cos a 2 z 2
n2
(z-1-z-2)/(1+z-1)3
ancos(n )
1 az 1 cos
1 2az 1 cos a 2 z 2
an
1/(1-az-1)
Связь Z-преобразования и преобразования Фурье
X z z e j X e
j
x n e
j n
n
Теоретические основы цифровой обработки сигналов. Слайд 30
30. Примеры Z-преобразования
ПримерZ1=e j /4 = 0.707 + j 0.707
Z2=e -j /4 = 0.707 - j 0.707
p1=0.9 e j /4 = 0.636 + j 0.636
p2=0.9 e -j /4 = 0.636 - j 0.636
1
|H(ej )|
0.9
0.8
|H(z)|
|H(ej 0.6
)|
1
5
0.4 4.5
0
3
2.5
-0.2
0.8
/4
3.5
z
Im(Z)
4
0.2
0.6
2
0.4
-0.4 1.5
1
-0.6
0.5
-0.8
0.2
0
-2
-1
-1.5
-1.5
0
0
-1
-1
-1
-0.5
-0.5
0
1
-0.5
20.5
3
01
Re(Z)
1.5
4
0.5
2
0
5
1
1
0.5
6
1.5
ImZ
ReZ
Теоретические основы цифровой обработки сигналов. Слайд 31
31. Пример
Основные свойства Z-преобразованияПоследовательность
x(n) y(n)
Z-преобразование
X(z) Y(z)
1. Линейность
a x(n)+b y(n)
a X(z)+ b Y(z)
2. Задержка
x(n-n0)
z-n0 X(z)
3. Частотный сдвиг
an x(n)
X(z/a)
4. Свертка
x(n) y(n)
X(z) Y(z)
x(n) y(n)
1
1
X
v
Y
z
/
v
v
dv
2 j c
Свойство
5. Произведение
Теоретические основы цифровой обработки сигналов. Слайд 32
32. Основные свойства Z-преобразования
Обратное Z-преобразованиеx n
1
n 1
X
z
z
dz
2 j c
Способы вычисления:
1. Деление числителя на знаменатель
2. Разложение на простые дроби
3. Использование теоремы о вычетах
4. Таблица Z-преобразований
Теоретические основы цифровой обработки сигналов. Слайд 33
33. Обратное Z-преобразование
Одностороннее Z-преобразованиеПредназначено для анализа физически реализуемых систем
X ( z ) x (n) z n
n 0
Основное отличие – в свойстве задержки
X z z n0 X1 z x1 n0 x1 n0 1 z 1
где
x1 n0 , x1 n0 1 ,
x1 1 z n 1 ,
, x1 1 - начальные условия
При нулевых начальных условиях:
X z X1 z z n0
- аналогично двустороннему Z-преобразованию
Теоретические основы цифровой обработки сигналов. Слайд 34
34.
Решение РУ с помощью Z-преобразованияj n
Пример: решить РУ y n x n ay n 1 , y( 1) K , x n e u 1 n
1
Решение: Y z X z a Y z z K
Y z
X z aK
1 az 1
,
- Z-преобразование от обеих частей
x n e j n X z
1
1 e j z 1
a a e j e j a e j
aK
1
aK
Y z
1
1
1
j 1
1
1 az
1 az
1 az
1 e j z 1
1 e z 1 az
j n 1
n 1
a
e
1
n 1
y n
u n
Y ( z ) a K
j
j 1
a e
a e
Общий случай решения РУ порядка L
L
L
i 0
i 1
y n ai x n i bi y n i , x (n) 0 при n 0
L
L
Y z ai z X z bi z 1Y z Y i Y 1 i z 1 ...
i 0
i
i 1
Теоретические основы цифровой обработки сигналов. Слайд 35
35. Решение РУ с помощью Z-преобразования
Пример вычисления обратного Z-преобразования2. Разложение на простые дроби:
30 z 2
X z 2
6z z 1
1. Деление числителя на знаменатель:
30 z 2
x n z
n
6z2 z 1
5
35 2
5 z 1
z ...
6
36
n
5
x 0 x 1 z ... 5 ...
6
1
5 35
x n 5, , ,...
6 36
i
Z 1
i pin
1
1 pi z
p1 1/ 2, p2 1/ 3
30 z 2
5
X z
6 z 1 2 z 1 3 1 1 1 1
1 z 1 z
2 3
X z
3
2
1
1
1 z 1 1 z 1
2
3
n
n
3 1 2 2 1 3 , при n 0
x n
при n<0
0,
Теоретические основы цифровой обработки сигналов. Слайд 36
36. Пример вычисления обратного Z-преобразования
3. Использование теоремы вычетовx n res X z z n 1
z c1
Определение вычета f(z) в полюсе порядка m:
1
d m 1
m
Re s f a
lim m 1 z a f z
m 1 ! z a dz
При m=1 и
30 z 2
X z 2
6z z 1
Re s f 1 2
30 1 2 1 2
2
2 6 1 2 1
n 1
f z
p z
g z
:
Re s f a
30 z 2 z n 1
f z 2
6z z 1
3 1 2 ;
n
Re s f 1 3
p a
g a
1
p1 ;
2
1
p2 ;
3
30 1 3 1 3
2
2 6 1 3 1
3 1 2 n 2 1 3 n ,
x n Re s f 1 2 Re s f 1 3
0,
n 1
2 1 3 ;
ï ðè n 0
ï ðè n 0
Теоретические основы цифровой обработки сигналов. Слайд 37
n
37. Пример вычисления обратного Z-преобразования
Дискретное преобразование ФурьеДискретное преобразование Фурье размерностью N:
N 1
X p k xp n e
j
2
kn
N
k 0, 1 ... N 1
,
n 0
Xp(k) – периодическая последовательность с периодом N
Обратное дискретное преобразование Фурье:
N 1
1
xp n X p k e
N k 0
j
2
kn
N
,
n 0, 1 ... N 1
xp(n) – периодическая последовательность с периодом N
Теоретические основы цифровой обработки сигналов. Слайд 38
38. Дискретное преобразование Фурье
Связь Z-преобразования и ДПФПусть
x n , при 0 n N 1
x n p
0,при других n
Тогда
X z x n z
n
Полагая
zk e
j
2
k
N
– конечная последовательность
N 1
x n z n
n 0
, k=0,1..N-1
X p (k ) X z
N 1
2
k
z e N
j
x n e
j
2
nk
N
n 0
Im(Z)
N=8
Re(Z)
0
Теоретические основы цифровой обработки сигналов. Слайд 39
39. Связь Z-преобразования и ДПФ
Связь ДПФ и ПФ2
N 1
j
kn
1
n
N
X z x n z X p k e
z n
n 0
n 0 N k 0
N 1
N 1
x(n)
1
X p k e
k 0 N
n 0
N 1
N 1
X e
где:
j
X ( z)
( )
j
2
k
N
N
N 1 X
k
1
z
z 1 p
2
j
k
N
k 0
1
N
1 z e
n
2 k
X
k
,
p
j
z e
N
k 0
N 1
N
sin
j N 1
2
e 2 ,
N sin
2
Ф(0)=1 :
X(ej2 k/N)=X(k)
Теоретические основы цифровой обработки сигналов. Слайд 40
40. Связь ДПФ и ПФ
Связь ПФ и ДПФ (пример)x (n)
xp(n)
0
N
|X (ej )|
0
n
4
2N
(k)
|Xp(k)|
2
N
arg[X (ej )]
0
2N
arg[Xp(k)]
2
N
4
2N
Теоретические основы цифровой обработки сигналов. Слайд 41
(k)
41. Связь ПФ и ДПФ (пример)
Дополнение нулямиx(n) – конечная последовательность длины N,
X (e j )
X (e j ) x(n) e j n
N 1
l
X e j (2 / L )l x(n) e j (2 / L )ln , l 2 l / L, l 0,1..L 1
n 0
x(n), 0 n N 1,
ˆx(n)
N n L 1,
0,
L 1
N 1
n 0
n 0
Xˆ k xˆ (n) e j (2 / L ) kn x(n) e j (2 / L ) kn
Xˆ k X e j (2 / L ) k
X(ej ), X9(k), X16(k)
-0.5
0
-0.5
Теоретические основы цифровой обработки сигналов. Слайд 42
42. Дополнение нулями
Основные свойства ДПФСвойство
1. Линейность
2. Задержка
Последовательности с
периодом N
xN(n), yN(n)
N-точечное ДПФ
XN(k) YN(k)
a xN(n)+b yN(n)
a XN(k)+ b YN (k)
xN(n-n0)
3. Частотный сдвиг
4. Свертка
5. Произведение
xN k e
-
2
n0k
N
XN k e
-
2
n0k
N
XN(k-n0)
xN(n) yN(n)
XN(k) YN(k)
xN(n) yN(n)
1 N-1
XN (m)YN (k - m)
N m=0
Теоретические основы цифровой обработки сигналов. Слайд 43
43. Основные свойства ДПФ
Циклический сдвиг конечной последовательностиx6(n)
x6(n+2)=x6(n-4)
0
5
n
0
n
5
Если xN(n), yN(n) -действительные
Re X N k Re X N N k
Im X N k Im X N N k
6. Симметрия:
X N k X N N k
arg X k arg X N k
N
N
Пусть zN(n)=xN(n)+jyN(n)
Im X k 1 2 Im Z k Im Z N k
Re Y k 1 2 Im Z k Im Z N k
Im Y k 1 2 Re Z N k Re Z k
Re X N k 1 2 Re Z N k Re Z N N k
N
N
N
N
N
N
N
N
N
Теоретические основы цифровой обработки сигналов. Слайд 44
44. Основные свойства ДПФ
Примеры ДПФ1
1
x1(n)=u0(n),
x2(n)=u0(n-4),
x3(n)=u0(n-8)
arg[X1(k)], arg[X2(k)], arg[X3(k)]
2
|X1(k)|=|X2(k)|=|X3(k)|
1
0
0
-
0
10
20
30
40
50
60
0
-0.5
0
0.5
-0.5
Re[X1(k)], Re[X2(k)], Re[X3(k)]
1
0
0
-1
-1
0
0.5
0.5
Im[X1(k)], Im[X2(k)], Im[X3(k)]
1
-0.5
0
-0.5
Теоретические основы цифровой обработки сигналов. Слайд 45
0
0.5
45. Примеры ДПФ
|X(k)|x(n)=u-1(n),
16
1
10
0
0
100
200
300
400
500
x(n)
0-0.5
0
0.5
0
0.5
|X(k)|
16
1
10
0
100
200
300
400
500
0-0.5
Теоретические основы цифровой обработки сигналов. Слайд 46
46. Примеры ДПФ
Свертка последовательностей1. Циклическая (периодическая, круговая);
2. Линейная (апериодическая);
3. Секционированная;
4. Быстрая (на основе БПФ, на основе разложения на
короткие, на основе структурных свойств, на основе
ТЧП)
Теоретические основы цифровой обработки сигналов. Слайд 47
47. Свертка последовательностей
Циклическая сверткаN 1
y p n x p l hp n l
l 0
hp(n)
n
0
N=9
2N=18
xp(n)
0
N=9
n
2N=18
N=9
l
2N=18
N=9
2N=18
xp(l),hpp(3-l)
(4-l)
(1-l)
(2-l)
(7-l)
(5-l)
(6-l)
(0-l)
yp(n)
0
n
Теоретические основы цифровой обработки сигналов. Слайд 48
48.
Быстрая свертка на основе БПФy n x n h n Y k X k H k
x(n)
Дополнение
нулями
(опционально)
xp(n)
БПФ
Xp(k)
Yp(k)
h(n)
Дополнение
нулями
hp(n)
БПФ
ОБПФ
y(n)
Hp(k)
(опционально)
Для БПФ по основанию 2 выигрыш в кол. операций умножения
N / log 2 N 1
Теоретические основы цифровой обработки сигналов. Слайд 49
49. Быстрая свертка на основе БПФ
Линейная сверткаN n 1
y n x m h n m , n 0,1
m 0
N1 N 2 1
hp(n)
N1=4
0
3
xp(n)
0
n
12
M N1+N2-1
N2=8
7
12
n
12
n
yp(n)
N1+N2-1=11
0
10
Теоретические основы цифровой обработки сигналов. Слайд 50
50. Линейная свертка
Секционированные сверткиДля свертки последовательностей значительно различающихся по длине
1. Метод перекрытия с суммированием
N>>L
x(n)
n
M
h(n)
y0(n)
2M
N=3M
n
L
+
y1(n)
n
L+M-1
n
y2(n)
y(n)
M
+
M
M
L+M-1
L+2M-1
2M
n
L+3M-1
2M
n
L+3M-1
L+2M-1
Теоретические основы цифровой обработки сигналов. Слайд 51
51. Секционированные свертки
2. Метод перекрытия с накоплениемh(n)
x(n)
xy0(n)
xy1(n)
n
L
M
M
2M
n
N=3M
n
M+L-1
n
yx2(n)
M
2M
3M
3M+L-1
n
2M
yx3(n)
3M
n
3M
y(n)
4M
n
M
2M
3M
L+3M-1
Теоретические основы цифровой обработки сигналов. Слайд 52
52. Секционированные свертки
Раздел 2. Цифровые фильтрыКлассификация
По импульсной характеристике:
•С конечной импульсной характеристикой (КИХ,КИО)
•С бесконечной импульсной характеристикой (БИХ, БИО)
По реализации:
•рекурсивные
•нерекурсивные
y(n) F [ y(n 1), y (n 2),...x(n), x(n 1),...]
y (n) F [ x(n), x(n 1), x(n 2)...]
По назначению:
•Фильтрация во временной области (Сглаживание, удаление постоянной
составляющей, изменение формы, …)
•Фильтрация в частотной области (фильтры нижних частот (ФНЧ),
фильтры верхних частот (ФВЧ), полосовые (ПФ), режекторные (РФ),
многочастотные, фазовые (всепропускающие),…)
По свойству адаптации:
•Неадаптивные
•Адаптивные
По скорости дискретизации:
•Неизменяющие частоту дискретизации
•Изменяющие частоту дискретизации (дециматоры, интерполяторы)
Теоретические основы цифровой обработки сигналов. Слайд 53
53. Раздел 2. Цифровые фильтры
Структурные схемы цифровых фильтровРекурсивные фильтры
N
Прямая форма 1
i
b
z
i
Y ( z)
H ( z)
iN 0
X ( z)
i
a
z
i
N
Y ( z ) ai z
i 0
i
N
X ( z ) bi z ;
i
i 0
; a0
i 0
N
1;
N
a y(n i) b x(n i);
i
i 0
N
N
i 0
i 1
i 0
i
y (n) bi x(n i) ai y (n i)
z-1
z-1
b1
x(n)
z-1
b2
bn
b0
y(n)
-aN
z-1
-a2
-a1
z-1
z-1
Теоретические основы цифровой обработки сигналов. Слайд 54
54. Структурные схемы цифровых фильтров
Структурные схемы рекурсивных фильтровПрямая форма 2 (каноническая)
N
Y ( z)
1
H ( z)
N
bi z i H1 ( z ) H 2 ( z );
X ( z)
ai z i i 0
N
i 0
W ( z)
1
Y ( z)
H1 ( z )
N
;
H 2 ( z)
bi z i ;
X ( z)
W ( z ) i 0
a z i
i 0
i
N
w(n) x(n) ai w(n i );
i 1
x(n)
w(n)
a1
a2
N
y (n) bi w(n i )
b0
i 0
y(n)
z-1
b1
z-1
b2
z-1
-aN
bN
Теоретические основы цифровой обработки сигналов. Слайд 55
55. Структурные схемы рекурсивных фильтров
NКаскадная форма
H ( z)
i 0
N
i
a
z
i
1 bi z
Hi ( z)
;
1
1 ai z
либо
i 1
1 b1i z 1 b2i z 2
Hi ( z)
;
1
2
1 a1i z a2i z
b0
x(n)
H1(z)
yi(n)
bi
ai
........
H2(z)
xi(n)
z-1
K
b0 H i ( z );
i 0
1
где
i
b
z
i
y(n)
Hk(z)
xi(n)
yi(n)
z-1
z-1
a1i
b1i
z-1
a2i
b2i
Теоретические основы цифровой обработки сигналов. Слайд 56
56. Структурные схемы рекурсивных фильтров
Параллельная формаK
H ( z ) c H i ( z );
i 1
b
c N ;
aN
b0i b1i z 1
Hi ( z)
;
1
2
1 a1i z a2i z
b0i
Hi ( z)
;
1
1 a1i z
cN
H1
x(n)
y(n)
Hk
Теоретические основы цифровой обработки сигналов. Слайд 57
57. Структурные схемы рекурсивных фильтров
Структурные схемы нерекурсивных фильтровПрямая форма
Y ( z ) N 1
H z
h(i ) z i ;
X ( z ) i 0
N 1
y (n) h(i ) x(n i )
i 0
x(n)
Z-1
h(0)
h(1)
Z-1
Z-1
h(2)
Z-1
h(N-1)
S
y(n)
Фильтр с многоотводной линией задержки
(трансверсальный фильтр)
Теоретические основы цифровой обработки сигналов. Слайд 58
58. Структурные схемы нерекурсивных фильтров
Инверсная форма ЦФПрямая
Инверсная
y
y
x
x
+
z
z
x
x
z
+
z
y
y
x(n)
h(n-1)
-1
Z
h(n-3)
h(n-2)
+
-1
Z
+
-1
Z
h(0)
+
Теоретические основы цифровой обработки сигналов. Слайд 59
y(n)
59. Инверсная форма ЦФ
КИХ фильтр на основе интерполяционной формулы ЛагранжаN 1
N 1
Am
H ( z ) (1 z zn )
;
1
m 0 1 z zm
n 0
1
где Am
H zm
N 1
1
(1
z
m zn )
n 0, n m
Для N=3:
(1 z 1 z1 )(1 z 1 z2 )
(1 z 1 z1 )(1 z 1 z2 )
H ( z)
H ( z0 )
H ( z1 )
1
1
1
1
(1 z0 z1 )(1 z0 z2 )
(1 z1 z0 )(1 z1 z2 )
(1 z 1 z1 )(1 z 1 z2 )
H ( z2 )
1
1
(1 z2 z0 )(1 z2 z1 )
1
1-z-1z0
1
1-z-1z1
x(n)
1-z-1z0
1-z-1z1
1-z-1zN-1
y(n)
+
1
1-z-1zN-1
Теоретические основы цифровой обработки сигналов. Слайд 60
60. КИХ фильтр на основе интерполяционной формулы Лагранжа
Фильтр с частотной выборкойПолучается из ЦФ на основе формулы Лагранжа при: Z
N 1
При этом
[1 z e
1
j
2
n
N
] 1 z
N
e
2
n
N
, n=0,1...N
2
j
m
1
N
Am
H (e
) - отсчет ЧХ
N
;
n 0
1
1 z 1
1
H0/N
H1/N
1
1 z e
x(n)
n
j
j
2
N
y(n)
1-z-N
+
HN-1/N
1
1
1 z e
j
2
N 1
N
Теоретические основы цифровой обработки сигналов. Слайд 61
61. Фильтр с частотной выборкой
Лестничные (решетчатые) фильтрыПрименение:
•анализ и синтез речи;
•компрессия и декомпрессия данных;
•адаптивная фильтрация.
Физическая модель: каскадное соединение цилиндров разного
диаметра. Коэффициенты фильтра представляют часть энергии
волны, отраженной от границ раздела цилиндров разного диаметра.
Преимущества
• нечувствительны к
погрешностям коэффициентов
• при увеличении порядка
фильтра не требуется
перерасчет коэффициентов
имеющихся звеньев
• легко обеспечивается
устойчивость БИХ-структур
Недостатки
больше вычислительные
затраты по сравнению со
структурами прямой формы
Теоретические основы цифровой обработки сигналов. Слайд 62
62. Лестничные (решетчатые) фильтры
Нерекурсивный решетчатый фильтрy1(n)
+
+
x(n)
Z-1
yM(n)
y2(n)
+
K1
K2
KM
K1
K2
KM
Z-1
+
U1(n)
Z-1
+
U2(n)
yi (n) yi 1 n K i ui n 1 , i 1, 2,..., M 1
ui (n) K i yi 1 n ui 1 n 1 , i 1, 2,..., M 1
для первого звена:
y0 (n) x(n)
u0 ( n ) x ( n )
Теоретические основы цифровой обработки сигналов. Слайд 63
+
UM(n)
63. Нерекурсивный решетчатый фильтр
Рекурсивный решетчатый фильтрx2(n)
xN(n)
+
+
x1(n)
y(n)
+
+
KN
K2
K1
-KN
-K2
-K1
Z-1
UN(n)
+
U2(n)
Z-1
+
U1(n)
x(n) xN n
xi 1 (n) xi n K i ui 1 n 1 , i N , N 1,...,1
ui (n) K i xi 1 n ui 1 n 1 , i N , N 1,...,1
y (n) x0 n x1 (n) K1 y n 1
K0 1
Теоретические основы цифровой обработки сигналов. Слайд 64
Z-1
64. Рекурсивный решетчатый фильтр
Лестнично-решетчатый фильтрxN(n)
x2(n)
x1(n)
+
+
+
+
KN
K2
K1
-KN
-K2
-K1
Z-1
+
UN(n)
CN
Z-1
+
U1(n)
C1
U2(n)
CN-1
Z-1
C2
C0
y(n)
+
+
+
Теоретические основы цифровой обработки сигналов. Слайд 65
+
65. Лестнично-решетчатый фильтр
Фильтры скользящего среднегоПреимущества: оптимальный фильтр для подавления
случайного шума, простота реализации
Недостаток: плохие фильтрующие свойства в частотной области
1 M 1
y ( n)
x(n k )
M k 0
Для M=4:
y ( n)
x(n) x(n 1) x( n 2) x( n 3)
4
x(n)
Z-1
1/4
x(n-1)
1/4
x(n-2)
Z-1
1/4
S
Z-1
x(n-3)
1/4
y(n)
Теоретические основы цифровой обработки сигналов. Слайд 66
66. Фильтры скользящего среднего
Импульсная характеристика:Переходная характеристика:
n 1
, при n 0..M -1
H ( n) M
0, при других n
1
, при n 0..M -1
h( n) M
0, при других n
Для M=4:
1
0.25
0
исходный сигнал
n
0
после фильтра M=11
M=51
Теоретические основы цифровой обработки сигналов. Слайд 67
n
67. Фильтры скользящего среднего
Частотная характеристика:HM ( f )
sin( M f )
M sin( f )
|H5(f)|, |H11(f)|, |H31(f)|, дБ
0
-10
-20
-30
0
0.1
0.2
0.3
0.4
f
Теоретические основы цифровой обработки сигналов. Слайд 68
68. Фильтры скользящего среднего
Рекурсивная форма реализации фильтра:y ( n)
1
x(n) x(n 1) ... x(n M 1)
M
1
y (n 1) x(n 1) x(n) x(n 1) ... x(n M 2) x(n M 1) x(n M 1)
M
My(n)
1
y ( n)
x(n) x(n M ) y(n 1)
M
y(n)
xN(n)
-
+
1/M
Z-M
Z-1
Теоретические основы цифровой обработки сигналов. Слайд 69
69. Фильтры скользящего среднего
Каскадное соединение фильтров:x(n)
HM(f)
........
HM(f)
Частотная характеристика:
sin( M f )
H M ,L ( f )
M
sin(
f
)
h7,1, h7,2, h7,4
y(n)
L
H7,1, H7,2, H7,4 , дБ
0
0.2
HM(f)
-20
-40
0.1
-60
0
5
10
15
20
n
0
0.1
0.2
0.3
Теоретические основы цифровой обработки сигналов. Слайд 70
0.4
f
70. Фильтры скользящего среднего
Общая характеристика КИХ-фильтровПреимущества:
• абсолютно устойчивы;
• физически реализуемы;
• линейные ФЧХ, произвольные АЧХ;
• простой расчет шумов дискретизации;
• возможность использования БПФ.
Недостатки:
• большой порядок при высоких требованиях к скатам АЧХ.
• возможна некратная шагу дискретизации задержка в фильтре
Основные методы расчета:
• взвешивание;
• частотная выборка;
• оптимизация по Чебышеву.
Порядок расчета:
• аппроксимация АЧХ, расчет коэффициентов, выбор порядка;
• выбор схемы построения;
• расчет шумов квантования, выбор разрядности данных и коэф-тов;
• проверка моделированием.
Теоретические основы цифровой обработки сигналов. Слайд 71
71. Общая характеристика КИХ-фильтров
КИХ-фильтры с линейной фазойh(n), 0 n N-1 - отсчеты ИХ фильтра (действительные).
H (e j ) H (e j ) e j ( ) - ЧХ фильтра
( ) , - ЛФХ фильтра
const - фазовая задержка
N 1
H (e ) h(n)e j n H (e j ) e j
j
n 0
N 1
H (e ) cos h( n) cos n
j
Re :
n 0
Im :
N 1
H (e ) sin h(n) sin n
j
n 0
N 1
Im
:
Re
sin
Nn 01
cos
h(n) sin n
h(n) cos n
n 0
( )
*
Теоретические основы цифровой обработки сигналов. Слайд 72
72. КИХ-фильтры с линейной фазой
N 11. =0
0
h(n) sin n
n 0
N 1
h(0) h(n) cos n
n 1
h(0) - произвольное
h( n)
0, при n 0
2. 0
N 1
N 1
n 0
n 0
h(n) cos n sin h(n) sin n cos
N 1
h(n) sin[( n) ] 0
n 0
Откуда:
N 1
2
h( n) h( N 1 n)
Теоретические основы цифровой обработки сигналов. Слайд 73
73. КИХ-фильтры с линейной фазой
центр симметрииh(n)
N=11
=5
5
n
a) Фильтр вида 1: четная симметрия, N-нечетное
центр симметрии
h(n)
5
6
б) Фильтр вида 2: нечетная симметрия, N-четное
Теоретические основы цифровой обработки сигналов. Слайд 74
N=12
=5.5
n
74. КИХ-фильтры с линейной фазой
h(n), 0 n N-1 - отсчеты ИХ фильтра (действительные).H (e j ) H (e j ) e j ( ) - ЧХ фильтра
( ) ,
,
const - фазовая задержка
1. =0
h(0) - произвольное
h( n)
0, при n 0
2. 0
N 1
2
2
h( n) h( N 1 n)
Для нечетных N:
N 1
h
0
2
Теоретические основы цифровой обработки сигналов. Слайд 75
75. КИХ-фильтры с линейной фазой
центр антисимметрииh(n)
N=11
=5
n
5
a) Фильтр вида 3: четная антисимметрия, N-нечетное
центр антисимметрии
h(n)
N=10
=4.5
4
5
б) Фильтр вида 4: нечетная антисимметрия, N-четное
Теоретические основы цифровой обработки сигналов. Слайд 76
n
76. КИХ-фильтры с линейной фазой
Импульсные и частотные характеристики КИХ-фильтров c ЛФХВид 1. N-нечетное, h(n)-симметричная
N 1
h(n) h( N 1 n) n 0,1,...
2
N 1
2
N 1
H (e j ) exp j
a(n) cos n
2 n 0
N 1
N 1
N 1
a
(
n
)
2
h
n
a (0) h
n 1, 2,...
2
2
2
h(n)
N=9
N-1
N=19
n
a(n)
n
N-1
2
H * (e j )
0
2
n
Теоретические основы цифровой обработки сигналов. Слайд 77
77. Импульсные и частотные характеристики КИХ-фильтров c ЛФХ
Вид 2. N-четное, h(n)-симметричнаяh( n) h( N 1 n)
n 0,1,...
N
2
N 1
2
N 1
1
H (e j ) exp j
b
(
n
)
cos
n
2
2 n 1
N
b( n) 2h n
2
h(n)
n 1, 2,...
N=9
N-1
N 1
2
N=18
n
a(n)
H * (e j )
n
N-1
2
2
n
0
Теоретические основы цифровой обработки сигналов. Слайд 78
78. Импульсные и частотные характеристики КИХ-фильтров c ЛФХ
Вид 3. N-нечетное, h(n)-антисимметричнаяN 1
h(n) h( N 1 n), 0 n N 1, h
0
2
N 1
N 1 2
H (e ) j exp j
c(n)sin n
2 n 1
N 1
N 1
n 1, 2,...
c ( n) 2h
n
2
2
j
h(n)
N-1
n
c(n)
H * (e j )
0
n
N-1
2
2
Теоретические основы цифровой обработки сигналов. Слайд 79
79. Импульсные и частотные характеристики КИХ-фильтров c ЛФХ
Вид 4. N-четное, h(n)-антисимметричнаяh(n) h( N 1 n), 0 n N 1
N
2
N 1
1
H (e j ) j exp j
d
(
n
)sin
n
2
2 n 1
N
d ( n) 2h n
2
n 1, 2,...
N
2
h(n)
N-1
n
d(n)
H * (e j )
0
n
N
2
2
Теоретические основы цифровой обработки сигналов. Слайд 80
80. Импульсные и частотные характеристики КИХ-фильтров c ЛФХ
Проектирование КИХ-фильтров методом взвешиванияЗадача проектирования
Заданы требования к АЧХ:
1 – неравномерность в полосе пропускания (ПП);
2 – неравномерность в полосе заграждения (ПЗ);
p – граничная частота полосы пропускания;
s – граничная частота полосы заграждения.
H * (e j )
2
p
s
Определить:
N-порядок фильтра,
h(n), n=0, 1 ... N-1 – коэффициенты фильтра
Теоретические основы цифровой обработки сигналов. Слайд 81
81. Проектирование КИХ-фильтров методом взвешивания
Явление ГиббсаПоскольку:
H (e ) h(n)e j n
j
n
то:
1 2
j
j n
h( n)
H
(
e
)
e
d , n 0, 1, 2,...
0
2
Если H(ej ) идеальная, то имеются два затруднения:
1. h(n) – бесконечная
усечение до N/2
2. Физически нереализуемая
сдвиг на N/2 вправо
H*(ej ) - идеал.
N1>N2
p s
C
2
Теоретические основы цифровой обработки сигналов. Слайд 82
82. Явление Гиббса
Проектирование КИХ-фильтров методом взвешиванияОперации метода взвешивания
Способ 1
1. выбрать N и w(n)
2. вычислить W (e
j
Способ 2
1. выбрать N и w(n)
)
2.
hˆ(n) h(n) w(n)
) ДПФ hˆ(n)
ˆ (e j ) H (e j ) *W (e j )
3. H
ˆ (e
3. H
4. проверка 1, 2, wp, ws
4. проверка 1, 2, wp, ws
5.
j
hˆ(n) ОДПФ Hˆ (e j )
Теоретические основы цифровой обработки сигналов. Слайд 83
83. Проектирование КИХ-фильтров методом взвешивания
в частотной областиH * (e j )
0
*
во временной области
h(n)
идеальный
ФНЧ
бесконечная
нереализуемая
j
W (e )
0
w(n)
Hˆ (e ) H (e ) * W (e )
j
n
0
j
j
N-1
2
0
N-1
2
0
N-1
2
ˆ
h(n) h(n) w(n)
N-1
2
N 1
g (n) hˆ n
2
Теоретические основы цифровой обработки сигналов. Слайд 84
n
n
84. Проектирование КИХ-фильтров методом взвешивания
Основные виды оконных функцияТребования к окнам:
- минимальный уровень боковых лепестков (min пульсаций АЧХ фильтра);
- минимальная ширина главного лепестка АЧХ окна (min ширина
переходной полосы фильтра).
1. Прямоугольное окно
N 1
N 1
n
1,
wR (n)
2
2
0, остальные N
WR (e j )
sin(
sin
N
)
2
2
Теоретические основы цифровой обработки сигналов. Слайд 85
85. Основные виды оконных функция
2. Обобщенное окно Хемминга2 n
wн (n) wR (n) (1 ) cos
N
2
2
j
j
1
1
j
j
N
N
Wн (e ) WR (e )
WR e
WR e
2
2
2
N
N
N
2
2
N
0
2
N
N
N
N
Теоретические основы цифровой обработки сигналов. Слайд 86
86. Основные виды оконных функция
3. Окно Кайзера2
2n
I0 1
N 1
wK (n)
I0 ( )
sin
W (e j )
/
1
2
/ 1
K
2
4. Окно Ланцоша
2 n
sin N 1
wL (n)
2
n
N 1
L
Теоретические основы цифровой обработки сигналов. Слайд 87
87. Основные виды оконных функция
Весовые функции окон и их ЧХВесовые функции
1
Весовые функции
Модуль ЧХ
0
1
0
-20
-20
0.5
0.5
-40
0
20
40
n -60
-40
-0.5
прямоугольное
1
0
0.5
0
0
20
40
n -60
-0.5
0
0.5
-0.5
0
0.5
Блекмана-Хэрриса
1
0
-20
-20
0.5
0.5
-40
0
Модуль ЧХ
20
40
n -60
-40
-0.5
Фейера
0
0.5
0
20
40
n -60
Чебышёва
Теоретические основы цифровой обработки сигналов. Слайд 88
88. Весовые функции окон и их ЧХ
Основные характеристики некоторых оконВид окна
Максимальный
уровень
бокового
лепестка, дБ
Асимтотическая
скорость спадания
бокового лепестка,
дБ/октава
Эквивалент
ширины
полосы
1. Прямоугольное
-13.3
-6
1.00
2. Треугольное
-26.5
-12
1.33
3. Ханна
-31.5
-18
1.50
4. Хемминга
-43
-6
1.36
5. Наттола
-98
-6
1.80
6. Гауссовское
-42
-6
1.39
7. Чебышёва
-50
0
1.39
Теоретические основы цифровой обработки сигналов. Слайд 89
89. Основные характеристики некоторых окон
Проектирование методом частотной выборкиN 1
X p k xp n e
n 0
j
2
kn
N
2
j
kn
1 N 1
N
xp n X p k e
N k 0
ДПФ
1 z N N 1
X z
N k 0
ОДПФ
X p k
1 z 1e
j
2
k
N
1. Произвести дискретизацию в N равноотстоящих точках на единичной
окружности
2. По этим точкам интерполировать непрерывную ЧХ
Теоретические основы цифровой обработки сигналов. Слайд 90
90. Проектирование методом частотной выборки
1+ 1 Ĥ(ej ), H(ej )1- 1
1+ 2
1- 0
2
s
2
p
Ĥ(ej )
T1
T2
T3
0
ПП
переходная
полоса
ПЗ
Теоретические основы цифровой обработки сигналов. Слайд 91
91. Проектирование методом частотной выборки
Проектирование оптимальных КИХ-фильтровКритерий оптимальности:
Вид аппроксимации ЧХ:
Процедура оптимизации:
Min. max. ошибки аппроксимации
a (n) cos n
Чебышевская
Итерационный алгоритм замены
Аппроксимация ЧХ фильтра
H * (e j ) Q(e j ) P(e j )
Вид фильтра
Вид 1
Q(ejw)
1
P(ejw)
N 1
2
a(n) cos n
n 0
Вид 2
cos ( /2)
N
1
2
b (n) cos n
n 0
Вид 3
sin
N 3
2
c (n) cos n
n 0
Вид 4
sin ( /2)
N
1
2
d (n) cos n
n 0
Теоретические основы цифровой обработки сигналов. Слайд 92
92. Проектирование оптимальных КИХ-фильтров
Постановка задачи проектированияD(e j ) - заданная ЧХ фильтра (идеальная);
W (e j ) - весовая функция ошибки аппроксимации.
Взвешенная функция ошибки аппроксимации
E (e j ) W (e j ) D(e j ) H * (e j )
т.к.
j
j
D(e j )
j
P
(
e
)
то: E (e ) W (e )Q(e )
j
Q (e )
j
H (e ) Q(e ) P(e )
*
j
Обозначая:
Wˆ (e ) W (e )Q(e )
Получим:
E (e j ) Wˆ (e j ) Dˆ (e j ) P(e j )
j
j
j
j
j
j
D
(
e
)
j
и Dˆ (e )
Q(e j )
max E (e j ) min
a ( n ), b ( n )
A
- критерий оптимальности
c ( n ), d ( n )
Теоретические основы цифровой обработки сигналов. Слайд 93
93. Постановка задачи проектирования
Графическая интерпретация задачи проектированияDˆ (e j )
P (e j )
Wˆ (e j )
5
2
0
D (e j ) P (e j )
E (e j )
max E (e j )
0
A
Теоретические основы цифровой обработки сигналов. Слайд 94
94. Графическая интерпретация задачи проектирования
Теорема Чебышеваr 1
j
Если P (e ) a ( n)cos n , то необходимое и достаточное условие,
n 0
что P(ej ) наилучшая аппроксимация по минимальному критерию функции
Dˆ (e j )
, состоит в наличии не менее r+1 экстремума функции E(ej )
в области А т.е. для
1< 2< 3 ... < r+1
E (e j i ) E (e j i 1 ), i 1, 2,..., r
j
j
E (e ) max E (e )
A
j
P (e )
1
2
0
2
ˆ (e j )
D
i
Теоретические основы цифровой обработки сигналов. Слайд 95
95. Теорема Чебышева
Решение задачи оптимизацииK
* j i
j
H
(
e
)
D
(
e
)
j
W (e )
* j
dH (e )
0; i 1, 2... r
i
d
Сущность итерационного алгоритма :
Избежать решения системы нелинейных уравнений относительно
экстремальных частот путем итерационной процедуры их уточнения и
решения системы из r+1 линейных уравнений относительно r
коэффициентов и погрешности .
Теоретические основы цифровой обработки сигналов. Слайд 96
96. Решение задачи оптимизации
Процедура проектирования оптимальных фильтров1. Задание D(ej ), W(ej ) и N
Задать r+1 экстремумов
2. Пересчет Dˆ (e j ), Wˆ (e j ) и P(e j )
3. Решение задачи аппроксимации
4. Расчет ИХ фильтра h(n)
Рассчитать 1, 2
Интерполировать P(ej )
P(ej )
1+ 1
1+
1
1
1- 1
1-
1
Рассчитать E(ej ), найти
экстремумы |E(ej )|>
Да
Экстремумы
изменились?
Нет
2
- 2
Наилучшая
аппроксимация
Теоретические основы цифровой обработки сигналов. Слайд 97
97. Процедура проектирования оптимальных фильтров
Свойства оптимальных ФНЧШирина переходной полосы:
Параметры оптимального ФНЧ:
N, Fp, Fs, K
дБ
0
-20
-40
-60
-80
100
1
F=Fs-Fp
Оценка качества фильтра нормированная ширина переходной
полосы
K 1
2
D=(N-1) F
2
При N (>50) D не зависит от N
0 0.1 0.2 0.3 0.4 0.5
Fp Fs
f
4
D
1=0.01
3
1=0.05
2
1=0.5
1
0
-100
1=0.1
-75
-50
-25
Теоретические основы цифровой обработки сигналов. Слайд 98
0
lg 2
98. Свойства оптимальных ФНЧ
Сравнение КИХ ФНЧ, спроектированных разными методами6
5
D=D(d1,d2)
Метод взвешивания (окно Кайзера)
d1=d2
Фильтры с частотной выборкой
d1=1.4*10-2...5.6*10-2
4
3
Оптимальные ФНЧ
2
1
0
10-5 10-4 10-3 10-2
1=10-2
1=2*10-2
1=5*10-2
1=10-1
2
-1
10
Теоретические основы цифровой обработки сигналов. Слайд 99
99. Сравнение КИХ ФНЧ, спроектированных разными методами
БИХ-фильтры с линейной ФЧХМетод 1
x(n)
Инверсия a(n)
X(z) времени A(z)
a(n)=x(-n)
f(n)
H(z)
F(z)
Инверсия b(n)
времени B(z)
b(n)=f(-n)
H(z)
A( z ) X ( z 1 )
F ( z ) H ( z ) A( z ) H ( z ) X ( z 1 )
B( z ) F ( z 1 ) H ( z _1 ) X ( z )
Y ( z ) H ( z ) B( z ) X ( z) H ( z) H ( z 1 )
H ЭКВ ( z ) Y ( z ) / X ( z ) H ( z ) H ( z 1 )
j
j
H ЭКВ (e ) H (e )
2
(e j ) 0
Теоретические основы цифровой обработки сигналов. Слайд 100
y(n)
Y(z)
100. БИХ-фильтры с линейной ФЧХ
Метод 2x(n)
g(n)
H(z)
Инверсия a(n)
времени
A( z ) X ( z 1 )
H(z)
f(n)
Инверсия
времени
F ( z ) H ( z ) X ( z 1 )
B( z ) F ( z 1 ) H ( z 1 ) X ( z )
G( z) H ( z) X ( z)
Y ( z ) B( z ) G ( z ) X ( z ) H ( z ) H ( z 1 )
H ЭКВ ( z ) H ( z ) H ( z 1 )
H ЭКВ (e j ) 2 H (e j ) cos ( )
Теоретические основы цифровой обработки сигналов. Слайд 101
+
y(n)
b(n)
101. БИХ-фильтры с линейной ФЧХ
Всепропускающие фильтрыНазначение: линеаризация ФЧХ.
Необходимое условие:
должен существовать нуль
для каждого полюса
p re j
1
z e j
r
(1/2;
(1/2;-
arg( H (e j ))
(2;
(2;-
1 j 1 j
2
1
2
z
e
z
e
z
z
cos
r
r
2
r
r
H ( z)
2
2
j
j
z
2
rz
cos
r
z re z re
0.25
0.5
r 2 z 2 2rz cos 1
2 2
r ( z 2rz cos r 2 )
H (e j ) const
Теоретические основы цифровой обработки сигналов. Слайд 102
102. Всепропускающие фильтры
Классификация методов расчета БИХ-фильтровЗадача аппроксимации АЧХ, ФЧХ, ГЗ или ИХ за счет выбора
коэффициентов фильтра.
N
H ( z)
b z
Y ( z)
iN 0
X ( z)
i
i
i
a
z
i
; a0
1;
i 0
3 группы методов расчета:
•расчет ЦФ по фильтрам непрерывного времени;
•прямые методы расчета разложения и количества нулей и полюсов в
Z-плоскости;
•оптимизация при наличии ограничений.
Теоретические основы цифровой обработки сигналов. Слайд 103
103. Классификация методов расчета БИХ-фильтров
Расчет ЦФ по фильтрам непрерывного времениАналоговые фильтры-прототипы: Баттерворта, Чебышева I и II
рода, Кауэра-Золотарева (эллиптические).
M
M
Системная функция:
b S
H ( S ) iN 0
i
i
i
a
S
i
i 1
(S c )
iN 0
i
(S d )
i 1
i
d i y(t ) M d i x( )
ai
bi
i
i
dt
dt
i 0
i 0
N
дифференциальное уравнение:
Методы дискретизации аналоговых фильтров:
1. Отображение дифференциалов;
2. Инвариантного преобразования ИХ;
3. Билинейного преобразования;
4. Согласованного Z-преобразования.
Теоретические основы цифровой обработки сигналов. Слайд 104
104. Расчет ЦФ по фильтрам непрерывного времени
Метод билинейного преобразованияУсловия однозначного преобразования аналоговых
фильтров в цифровые
1.
2.
Ось j должна отображаться в единичную окружность в Z-плоскости
(сохранение частотно-избирательных свойств).
Левая полуплоскость S-плоскости должна отображаться внутрь
единичной окружности (сохранение устойчивости)
Im Z
j
j
0
-1
1
0
Re Z
-j
S-плоскость
Z-плоскость
Условия 1 и 2 удовлетворяются отображением:
2 (1 z 1 )
2/T S
S
z
T (1 z 1 )
2/T S
- билинейное преобразование
Теоретические основы цифровой обработки сигналов. Слайд 105
105. Метод билинейного преобразования
При S=j - частотная ось S-плоскости:2
j
z T
z 1
2
0, z 1
j
, z 1
T
Полагая S= +j :
2
j
z T
при 0, z 1
2
j
T
- 1ое условие выполняется
- 2ое условие выполняется
Аналоговый фильтр с H(S) преобразуется в цифровой с H(z):
H ( z) H (S )
2 1 z 1
S
T 1 z 1
Порядок знаменателя сохраняется, а порядок числителя может возрастать
1
H (S )
S a
1
1 z 1
H ( z)
2
2
2 1 z 1
1
a
z
a
a
T
T
T 1 z 1
Нуль H(S) при S
отображается в z=-1
Теоретические основы цифровой обработки сигналов. Слайд 106
106. Метод билинейного преобразования
H(j )2
Метод билинейного преобразования
АЧХ аналогового
фильтра
0
T
H(ej )
Нелинейное соотношение частот:
z e j T
j
S j
j
j T
T
2
j
T
2
2 (1 e
) 2 e e
T
j T
j
T (1 e
) T j 2T
e 2
2 T e
T
tg
2
2
АЧХ цифрового фильтра
T
- для фильтров с почти ступенчатой ЧХ нелинейная связь частотных шкал
может быть скомпенсирована;
- ни ФЧХ, ни импульсная характеристики аналогового и цифрового фильтра
не совпадают
Теоретические основы цифровой обработки сигналов. Слайд 107
107. Метод билинейного преобразования
Частотные преобразованияМетод 1
Расчет аналогового ФНЧ с=1
Преобразование
полосы частот
Аналог-аналог
Дискретизация
фильтра
ЦФ с заданными
хар-ками
Преобразование частот аналоговых фильтров
Метод 2
Расчет аналогового ФНЧ с=1
Дискретизация
фильтра
Преобразование
полосы частот
ЦФ с заданными
хар-ками
Преобразование частот цифровых фильтров
Теоретические основы цифровой обработки сигналов. Слайд 108
108. Частотные преобразования
Преобразование полосы частот по методу 1L - нижняя частота среза;
U - верхняя частота среза.
Вид преобразования
Замена переменной
1. ФНЧ ФНЧ
S S U
2. ФНЧ ФВЧ
S U S
3. ФНЧ ПФ
S 2 U L
S
S ( U L )
4. ФНЧ РФ
S
S ( U L )
S 2 U L
Уровень пульсаций в полосе пропускания и полосе задержки не изменяется;
С теоретической и расчетной точки зрения оба метода равноценны.
Теоретические основы цифровой обработки сигналов. Слайд 109
109. Частотные преобразования
Сравнение КИХ и БИХ-фильтровОптимальные КИХ-фильтры - эллиптические БИХ.
На обработку 1 отсчета требуется MAC операций (мин.):
N 1
2 - операций MAC для КИХ-фильтра N-го порядка
3n 3
2 - операций MAC для БИХ-фильтра n-го порядка
Для фильтров одинаковой вычислительной сложности:
3n 3 N 1
2
2
N
1
3
n
n
Теоретические основы цифровой обработки сигналов. Слайд 110
110. Сравнение КИХ и БИХ-фильтров
N/n Fp=0.15, 1=0.10.001
30
20
2=0.1
30
0.01
0.0001
10
2
4
6
Fp=0.35, 1=0.00001
N/n
8
0.00001
N/n=3
n
2=0.1
20
10
2
4
6
8
0.01
0.001
0.0001
0.00001
N/n=3
n
1. При Fp>0.3 БИХ-фильтр лучше при любых 1, 2, n.
2. При n 7 БИХ-фильтр лучше при любых 1, 2, Fp.
3. КИХ-фильтр лучше при большой 1 и малой 2.
4. КИХ-фильтр лучше при линейной ФЧХ.
Теоретические основы цифровой обработки сигналов. Слайд 111
111. Сравнение КИХ и БИХ-фильтров
Фильтры изменяющие частоту дискретизацииХарактерная особенность: различная скорость потока данных на входе и
выходе.
Применения:
• преобразование частоты дискретизации между цифровыми
аудиосистемами;
• узкополосные ФНЧ и полосовые фильтры;
• сжатие полосы частот при цифровой обработке речевых сигналов;
• трансмультиплексоры (преобразование ВРК-ЧРК);
• квадратурная модуляция;
• восстанавливающие и ограничивающие фильтры в цифровых
аудиосистемах;
• узкополосный анализ спектра в сонарных системах и вибрационном
анализе.
Основные операции: прореживание (децимация) и интерполяция.
Теоретические основы цифровой обработки сигналов. Слайд 112
112. Фильтры изменяющие частоту дискретизации
|X(f)|x(nT)
t
T
yy(nT/2)
1(nT/2)
0
Интерполяция 2 x(nT)
fs/2
fs 2fs/2 2fs
f
|Y
|Y(f)|
1
0(f)|
t
T/2
fs/4
fs/2
fs
f
Децимация 3 y(nT/2)
y(nT/2)
z0(3nT/2)
3T/2
|Z
|Y(f)|
0(f)|
t
fs/3fs/22fs/3
Теоретические основы цифровой обработки сигналов. Слайд 113
fsfs
f
113. Фильтры изменяющие частоту дискретизации
Для устранения наложения при прореживании и для снижения искаженией вспектре при интерполяции необходимо выполнять низкочастотную
фильтрацию, согласованную с коэффициентом изменения частоты
дискретизации.
|X(f)|
АЧХ ФНЧ дециматора
f
fs
fs/2
Прореживание сигнала в 2 раза
|Y1(f)| |Y2(f)|
f
fs1/2
fs1=fs/2
3fs1/2
2fs1
Теоретические основы цифровой обработки сигналов. Слайд 114
114. Фильтры изменяющие частоту дискретизации
LH(z)
H(z)
Интерполятор
M
Дециматор
h(0)
x(n)
L
Z-1
h(1)
Z-1
h(2)
Z-1
S
y(m)
Z-1
h(N-1)
Интерполирующий фильтр
Теоретические основы цифровой обработки сигналов. Слайд 115
115. Фильтры изменяющие частоту дискретизации
h(0)x(n)
h(0)
x(n)
M
Z-1
Z-1
h(1)
h(1)
M
Z-1
h(2)
-1
Z
S
Z-1
M
h(2)
y(m)
M
-1
Z
Z-1
S
Z-1
h(N-1)
h(N-1)
M
Прореживающий фильтр
В отличие от рекурсивных, нерекурсивные структуры дециматоров
обеспечивают возможность работы умножителей на частоте выходного
сигнала. При больших частотах дискретизации, в дециматорах часто
используют гребенчатые фильтры.
Теоретические основы цифровой обработки сигналов. Слайд 116
y(m)
116. Фильтры изменяющие частоту дискретизации
Спектральный анализМетоды цифрового спектрального анализа
Основные приложения:
радиолокация, радионавигация, радиоастрономия;
гидроакустика, гидролокация;
системы распознавания речи;
сжатие полосы речевых сигналов;
вибрационный анализ.
Спектральный анализ – это измерение, которое дает точные или
приближенные значения Z - преобразования дискретного сигнала в
заданном множестве точек
Z - плоскости.
Различают “мгновенный” спектр и оценку спектральной плотности мощности.
Разновидности спектрального анализа:
вычисление “мгновенного” спектра с использованием окон;
оценивание СПМ классическими методами;
оценивание СПМ параметрическими методами:
оценивание блочных данных;
рекурсивное оценивание;
многомерный спектральный анализ.
Теоретические основы цифровой обработки сигналов. Слайд 117
117. Спектральный анализ
Алгоритмы БПФБыстрое преобразование Фурье (БПФ) – метод вычисления ДПФ
{x(n)}, 0 n N-1 – комплексный сигнал.
N 1
ДПФ:
X ( k ) x ( n) e
N 1
j
2
nk
N
, где k 0,1,2...N-1
n 0
X (k ) x (n) W
nk
где
W e
j
2
N
- множитель вращения
n 0
{Wnk} периодична по n и k с периодом N:
W(n+mN)(k+lN) = (WN)nk , где m, l = 0, 1, 2…, WN – множитель вращ-я с периодом N.
Количество операций для ДПФ размерности N:
(N-1)2 – комплексных умножений, N(N-1) – комплексных сложений.
Основная идея БПФ – разбиение длинной последовательности на короткие.
N/2
N
Кол ~
N2
ДПФ
Кол=N2/4
ДПФ
Кол=N2/2
N/2
ДПФ
Кол=N2/4
Теоретические основы цифровой обработки сигналов. Слайд 118
118. Алгоритмы БПФ
Алгоритм БПФ с прореживанием по времениПусть N – степень 2.
Разобьем {x(n)} на {x1(n)} – четные отсчеты, {x2(n)} – нечетные отсчеты.
N
x1(n) = x(2n), x2(n) = x(2n+1), для n 0,1... 1
2
N 1
N
1
2
N
1
2
n 0
n 0
n 0
X (k ) x(n) WNnk x(2n) WN2 nk x(2n 1) WN(2 n 1) k
Поскольку WN2 [e
j
2
N 2
] e
2
j
N
2
N
1
2
WN
N
1
2
то X (k ) x1 (n) WNnk WNk x2 (n) WNnk
2
2
n 0
X1 ( k )
2
n 0
X 2 (k )
k
Тогда X (k ) X 1 (k ) WN X 2 (k )
Вычисление X1(k) и X2(k) – 2N 2/4 MAC + объединение X1(k) и X2(k) – N MAC
Всего N 2/2+N N 2/2 при больших N
Теоретические основы цифровой обработки сигналов. Слайд 119
119. Алгоритм БПФ с прореживанием по времени
Доопределение X(k) для k N/2 на основании периодичности N/2 точечных ДПФ:N
k
X
(
k
)
W
X
(
k
),
0
k
1
N
2
1
2
X (k )
X (k N ) W k X (k N ), N k N 1
N
2
1
2
2
2
Из-за WNk - период X(k) не равен периоду X1(k).
k
Т.к. W WN
k
N
N
2
N
k
X
(
k
)
W
X
(
k
),
0
k
1
N
2
1
2
то X (k )
N
k
N
X (k ) W 2 X (k N ), N k N 1
N
2
1
2
2
2
Теоретические основы цифровой обработки сигналов. Слайд 120
120. Алгоритм БПФ с прореживанием по времени
Пример алгоритма БПФ размерности 8 по основанию 2 спрореживанием по времени
Разложение ДПФ размерности 8 на два ДПФ размерности 4.
Стадия 3
x1(1)=x(2)
x1(2)=x(4)
x1(3)=x(6)
x2(0)=x(1)
x2(1)=x(3)
x2(2)=x(5)
x2(3)=x(7)
4-х
точечн.
ДПФ
4-х
точечн.
ДПФ
X1(1)
"бабочка"
a
a+b
X(1)
X1(2)
X(2)
X1(3)
X(3)
X1(0)
X2(0)
X2(1)
X2(2)
X2(3)
X(0)
w 3 w 2 w 1 w 0
x1(0)=x(0)
X(4)
X(5)
b
a-b
a wk awk
X(6)
X(7)
Теоретические основы цифровой обработки сигналов. Слайд 121
121. Пример алгоритма БПФ размерности 8 по основанию 2 с прореживанием по времени
Стадия 2 X (k ) A(k ) W k B (k ) A(k ) W 2 k B (k ), 0 k N 11
N
N
2
2
N
k
2k
X 2 (k ) C (k ) WN D(k ) C (k ) WN D(k ), 0 k 1
2
2
c(0)=x2(0)=x(1)
c(1)=x2(2)=x(5)
d(0)=x2(1)=x(3)
d(1)=x2(3)=x(7)
2-х
точечн.
ДПФ
2-х
точечн.
ДПФ
X (0)
A(1)
X1(1)
X (1)
X1(2)
X (2)
X1(3)
X (3)
B(0)
B(1)
C(0)
X2(0)
C(1)
X2(1)
D(0)
D(1)
X2(2)
X2(3)
w1 w0
b(1)=x1(3)=x(6)
2-х
точечн.
ДПФ
X1(0)
w3 w2
b(0)=x1(1)=x(2)
Стадия 3
A(0)
w 2w 0
a(1)=x1(2)=x(4)
Стадия 2
w 2w 0
a(0)=x1(0)=x(0)
2-х
точечн.
ДПФ
X (4)
X (5)
X (6)
X (7)
Теоретические основы цифровой обработки сигналов. Слайд 122
122. Пример алгоритма БПФ размерности 8 по основанию 2 с прореживанием по времени
Направленный граф алгоритма БПФ размерности N = 8 по основанию 2с прореживанием по времени и с замещением (алгоритм Кули-Тьюки).
F (0) f (0) f1 WN0 f (0) f (1);
Стадия 1
N
F (1) f (0) f1 WN 2 f (0) f (1);
Стадия 1
x(0)
x(4)
w
Стадия 3
Стадия 3
X(0)
0
X(1)
0
x(2)
X(2)
w
2
w
X(3)
w0
w
0
0
x(3)
w
X(5)
w3
x(5)
X(4)
w1
x(1)
w2
x(6)
w
0
X(6)
2
x(7)
w
0
w
Теоретические основы цифровой обработки сигналов. Слайд 123
X(7)
123. Направленный граф алгоритма БПФ размерности N = 8 по основанию 2 с прореживанием по времени и с замещением (алгоритм
Свойства алгоритма БПФ по основанию 21. Алгоритм состоит из этапов. На каждом этапе происходит изменение
размерности БПФ вдвое по сравнению с предыдущим.
Kэт = log2 N
2. На каждом этапе необходимо выполнить N/2 операций “бабочка”.
A
B
K
X = A + B WN
2 операции комплексного сложения и
1 операция комплексного умножения
Y = A - B WNK
3. Общее число базовых операций "бабочка":
N
K оп log 2 N
2
4. Для вычисления базовой операции достаточно иметь одну
дополнительную ячейку для хранения произведения. Остальные результаты
размещаются в освободившиеся ячейки. Это алгоритм с замещением.
Теоретические основы цифровой обработки сигналов. Слайд 124
124. Свойства алгоритма БПФ по основанию 2
Сравнение вычислительных затратKДПФ/БПФ2
N2
K ДПФ / БПФ 2
N log 2 N
2500
КДПФ/БПФ2
2000
70
1500
50
30
10
0 5 10 15 20 25 30 N
1000
500
0
2
16
64
256
1024
4096
16384
N
Выигрыш в количестве операций алгоритма БПФ2 по сравнению с ДПФ в
зависимости от размерности N
Теоретические основы цифровой обработки сигналов. Слайд 125
125. Сравнение вычислительных затрат
Перестановка данных и двоичная инверсияДля алгоритма по основанию 2 и прореживанием по времени закон
чередования входных отсчетов описывается двоично-инверсным порядком.
Пример: N = 8 L = log2 8 = 3
№ п/п
0
1
2
3
4
5
6
7
Двоичное
представление
000
001
010
011
100
101
110
111
Двоичная
инверсия
000
100
010
110
001
101
011
111
Двоич.-инверс.
номер
0
4
2
6
1
5
3
7
Способы получения поворачивающих множителей
1. Табличный – требует много памяти, но имеет наибольшее быстродействие
2. Последовательный – не требует много памяти, но имеет низкое быстродейст.
3. Рекуррентный WNK WNK L WNL с изменением шага от этапа к этапу и
0
с начальным условием WN 1 на каждом этапе
Теоретические основы цифровой обработки сигналов. Слайд 126
126. Перестановка данных и двоичная инверсия
Алгоритм БПФ с прореживанием по частотеВходная последовательность разбивается на 2 половины:
N
x1 (n) x(n), при n 0, 1, 2 ... 1
2
N
N
x2 (n) x(n ), при n 0, 1, 2 ... 1
2
2
Тогда N-точечное ДПФ последовательности {x(n)}:
N
1
2
X ( k ) x ( n) W
nk
N
n 0
Т.к.
N
k
2
N
W
N 1
x ( n) W
nk
N
n
e j k
то
N
2
N
1
2
x1 (n) W
n 0
nk
N
N
1
2
(n
x2 (n) WN
n 0
N
1
2
X (k ) [ x1 (n) e j k x2 (n)] WNnk
n 0
Теоретические основы цифровой обработки сигналов. Слайд 127
N
)k
2
127. Алгоритм БПФ с прореживанием по частоте
Nk
2
N
Поскольку W
e j k 1 то X(k) для четных и нечетных k:
N
1
2
N
1
2
n 0
n 0
X (2k ) [ x1 (n) x2 (n)] WN2 nk [ x1 (n) x2 (n)] WNnk
2
f(n)
N
1
2
N
1
2
n 0
n 0
X (2k 1) [ x1 (n) x2 (n)] WNn (2 k 1) {[ x1 (n) x2 (n)] WNn } WNnk
2
g ( n)
X(2k) получаются из N/2-точечных ДПФ последовательности:
f(n) = x1(n) + x2(n) ; n = 0, 1, 2…N/2 – 1
X(2k+1) получаются из N/2-точечных ДПФ последовательности:
g(n) = [x1(n) - x2(n)]WNn n = 0, 1, 2…N/2 – 1
Теоретические основы цифровой обработки сигналов. Слайд 128
128. Алгоритм БПФ с прореживанием по частоте
Пример построения алгоритма БПФ размерности 8 спрореживанием по частоте
Стадия 1
X1 (u)
X(0)
- f(0) -
X(1)
- f(1) -
X(2)
- f(2) -
X(3)
- f(3) -
X(6)
X(7)
0
X2 (u)
X(5)
w 1 2
w
3
ww
X(4)
- g(0) - g(1) - g(2) - g(3) -
4-х
точечн.
ДПФ
4-х
точечн.
ДПФ
Теоретические основы цифровой обработки сигналов. Слайд 129
X(0)
X(4)
X(2)
X(6)
X(1)
X(5)
X(3)
X(7)
129. Пример построения алгоритма БПФ размерности 8 с прореживанием по частоте
Алгоритмы БПФ по основанию 2Направленный граф алгоритма БПФ по основанию 2 с прореживанием по частоте.
x(0)
X(0)
x(1)
X(4)
x(2)
X(2)
x(3)
X(6)
x(4)
X(1)
x(5)
X(5)
x(6)
X(3)
x(7)
X(7)
Теоретические основы цифровой обработки сигналов. Слайд 130
130. Алгоритмы БПФ по основанию 2
Различия алгоритмов БПФ с прореживаниемпо времени и по частоте
по времени
по частоте
1. Порядок следования входных отсчетов:
прямой
двоично-инверсный
2. Порядок следования выходных отсчетов:
прямой
двоично-инверсный
3. Базовая операция “бабочка”
A
B
K
X = A + B WN
Y = A - B WNK
A
B
X=A+B
Y = (A – B) W KN
Теоретические основы цифровой обработки сигналов. Слайд 131
131. Различия алгоритмов БПФ с прореживанием по времени и по частоте
Вычисление обратного ДПФ по алгоритму прямогоОбратное ДПФ {x(n)} для последовательности {X(k)}, k=0,1,…,N-1
1 N 1
x(n) X (k ) W nk
N k 0
N x ( n)
*
- обратное ДПФ
N 1
X (k ) W
*
nk
k 0
* - знак комплексного сопряжения
ДПФ послед-ти X * (k )
Тогда:
1 N 1 *
x(n) [ X (k ) W nk ]*
N k 0
Т.о. можно использовать алгоритмы БПФ для вычисления ДПФ и ОДПФ
Теоретические основы цифровой обработки сигналов. Слайд 132
132. Вычисление обратного ДПФ по алгоритму прямого
Алгоритмы БПФ по основанию 4По аналогии с основанием 2 можно построить алгоритмы БПФ по основанию 4.
ДПФ размерности 4 не требует операций комплексного умножения, так
2
как умножение на W exp j
выполняется перестановкой реальной и
4
мнимой компонент
3 комплексных
умножения
12 комплексных
сложений
Операция «бабочка» по основанию 4 с прореживанием по
времени
Выигрыш по количеству операций комплексного умножения по сравнению с
алгоритмом БПФ по основанию 2 около 25%.
Теоретические основы цифровой обработки сигналов. Слайд 133
133. Алгоритмы БПФ по основанию 4
Алгоритм БПФ по основанию 4 размерности 160
0
4
0
1
8
0
0
2
3
12
1
5
9
0
4
1
5
2
6
3
7
0
0
0
13
0
2
6
10
0
0
0
14
11
0
0
0
8
4
9
6
10
11
0
3
7
2
3
12
6
13
9
14
15
15
Теоретические основы цифровой обработки сигналов. Слайд 134
134. Алгоритм БПФ по основанию 4 размерности 16
Принцип построения алгоритма БПФ спроизвольным основанием
Если N – составное число, то одномерный массив отсчетов можно
записать в виде матрицы размерности N=MxL.
Алгоритм вычисления ДПФ размерности N:
Преобразовать одномерный массив в матрицу (заполнение по
строкам!) n m L l, n 0..N 1, m 0..M 1( №столбца), l 0..L 1( №строки).
M 1
Вычислить ДПФ каждого столбца X c k , l x m, l WMmk , k 0..M 1, l 0..L 1
m 0
Умножить элементы матрицы
Вычислить ДПФ каждой строки
X c k , l X c k , l WNkl , k 0..M 1, l 0..L 1
L 1
X r k , i X c k , l WLli , k 0..M 1, i 0..L 1
l 0
Преобразовать матрицу в одномерный массив (считывание по
строкам!).
Если размерность строки или столбца - составное число, разбиение
можно повторить.
Для произвольных составных N наиболее быстрый алгоритм со смешанным
основанием – АВПФ (алгоритм Винограда преобразования Фурье).
Теоретические основы цифровой обработки сигналов. Слайд 135
135. Принцип построения алгоритма БПФ с произвольным основанием
Сравнение БПФ и гребенки фильтров.X 0 i
+
Z-1
W0
X1 i
+
x i
W1
Z-N
X k i
+
Z-1
Wk
X N 1 i
+
выдает N спектральных отсчетов
в каждый момент времени;
Требует N операций умножениянакопления на 1 отсчет сигнала.
БПФ без перекрытия:
Z-1
-
Гребенка фильтров:
Z-1
WN-1
Анализатор спектра в виде гребенки
фильтров
Выдает N спектральных отсчетов
через N отсчетов сигнала;
1 log N
Требует
2
2
операций умножения-накопления
на 1 отсчет сигнала.
БПФ с перекрытием:
Выдает N отсчетов через N
K
отсчетов сигнала;
Требует в K раз больше
операций
Теоретические основы цифровой обработки сигналов. Слайд 136
136. Сравнение БПФ и гребенки фильтров.
Использование «окон» при спектральном анализеИмпульсная характеристика
2π k
exp
n , 0 n N -1
j
h
n
=
N
одного из гребенки фильтров:
Частотная характеристика
(без фазового множителя):
H e j
0, остальные n
N
sin
2
k
sin
2
N
k=0,1..N-1
Проблема: маскировка слабых спектральных компонент
сильными из-за высоких боковых лепестков АЧХ фильтра.
40
дБ
Амплитуды
сигналов:
30
20
А1 – 1 (0 дБ)
10
0
А2 – 0.01 (-40 дБ)
-10
А3 –0.001(-60 дБ)
-20
-30
200
300
400
500
600
700
800
Теоретические основы цифровой обработки сигналов. Слайд 137
137. Использование «окон» при спектральном анализе
Во временной области –умножение сигнала на весовую
функцию «окна».
В спектральной области – свертка
спектра сигнала с частотной
характеристикой «окна».
Временные отсчеты
Временные отсчеты
Умножение на
весовую функцию
Анализатор спектра
(БПФ)
Анализатор спектра
(БПФ)
Свертка с ЧХ «окна»
(сглаживание спектра)
Спектральные отсчеты
Спектральные отсчеты
1 умножение на отсчет для всех
видов окон
Для окна Ханна порядок фильтра -3
( окно Хэмминга – без умножений).
Для окна Блэкмана порядок
фильтра - 5.
Теоретические основы цифровой обработки сигналов. Слайд 138
138. Использование «окон» при спектральном анализе
дБ40
30
20
rectangular
window
Амплитуды
сигналов:
Hann
window
C hebyshev
window
А1 – 1 (0 дБ)
10
0
А2 – 0.01 (-40 дБ)
-10
А3 –0.001(-60 дБ)
-20
-30
-40
-50
200
300
400
500
600
700
800
Стратегия выбора «окна» по одному из параметров:
по скорости спадания БЛ – при большой разнице амплитуд и частот;
по максимальному уровню БЛ – при разных амплитудах и неизвестных
(распределенных в большом диапазоне) частотах;
по ширине основного лепестка АЧХ – при сопоставимых амплитудах и
близко расположенных частотах.
Теоретические основы цифровой обработки сигналов. Слайд 139
139. Использование «окон» при спектральном анализе
Классические методы спектрального оцениванияЗадача: получить оценку спектральной плотности мощности
сигнала с минимальной среднеквадратической ошибкой по
зашумленной реализации конечной длительности.
Основные характеристики:
Диапазон анализируемых частот
Определяется частотой дискретизации Fs:
от 0 до ½ Fs для действительных сигналов;
от - ½ Fs до + ½ Fs для комплексных сигналов.
Разрешающая способность по частоте
Определяется эффективной шириной
главного лепестка ЧХ окна Be:
Be
W k
k 0
W k
max
k 0, N 1
Достоверность
Определяется относительной
среднеквадратической ошибкой Q
оценки СПМ
N 1
Q k
S k S k
S k
2
2
, k 0,1..N 1
Теоретические основы цифровой обработки сигналов. Слайд 140
140. Классические методы спектрального оценивания
Особенность оценки СПМ при наличии шума:При увеличении размерности БПФ ошибка оценки СПМ не
уменьшается, так как определяется спектральной плотностью шума.
Для ее снижения необходимо усреднение спектральных оценок.
При ограниченной длине реализации случайного процесса:
Повышение достоверности оценки приводит к ухудшению
разрешающей способности;
Повышение разрешающей способности приводит к потере
достоверности оценки.
Если влияние шума пренебрежимо мало, то
Be Te 1
Te - эффективная длительность реализации.
Если необходимо усреднение оценок СПМ для повышения
достоверности, то Q Te BS 1
BS
N 1
W
k
k 0
N 1
W k
k 0
2
- статистическая ширина
2
полосы «окна»
Теоретические основы цифровой обработки сигналов. Слайд 141
141. Классические методы спектрального оценивания
Периодограммный метод оценки СПМПоследовательность операций:
1.
Реализация процесса длиной L отсчетов разбивается на M
сегментов размером N отсчетов каждый
xm n , n 0,1,..N 1, m 1,2..M .
2.
Вычисляется БПФ от каждого сегмента
X m k , k 0,1,..N 1, m 1, 2..M .
3.
Усредняется оценка СПМ
PX k 1
M
X m k X m* k , k 0,1..N 1
M m 1`
Для снижения потерь из-за взвешивания функцией «окна» применяется
перекрытие сегментов на ½ или ¼.
Увеличение
длины
сегмента
соответствует
улучшению
разрешающей способности и снижению достоверности
(возрастанию ошибки), и наоборот.
Теоретические основы цифровой обработки сигналов. Слайд 142
142. Периодограммный метод оценки СПМ
Коррелограммный метод оценки СПМОснован на дискретном аналоге теоремы Винера-Хинчина.
Последовательность операций:
1.
Вычислить АКФ реализации процесса в диапазоне [0,N-1]
дискретных задержек:
L 1
RX m x n x* n m , m 0,1..N 1.
n 0
2.
Вычислить ДПФ размерности N от АКФ c использованием «окна»:
2
PX k RX m exp j
k m , k 0,1..N 1.
N
m 0
N 1
Увеличение диапазона задержек АКФ соответствует улучшению
разрешающей способности, и снижению достоверности
(возрастанию ошибки), и наоборот.
Рекомендуется: начинать оценку СПМ с высокой достоверности,
продвигаясь в направлении более высокого разрешения по
частоте.
Теоретические основы цифровой обработки сигналов. Слайд 143
143. Коррелограммный метод оценки СПМ
Параметрические методы спектрального оцениванияОсновные недостатки классических методов:
• низкое разрешение, ограниченное длительностью сигнала;
• маскировка слабых сигналов боковыми лепестками «окон».
Возможность устранения этих недостатков – в использовании
априорной информации об оцениваемом процессе.
Задача оценки СПМ сводится к оценке небольшого числа
параметров модели.
Источник
«белого»
шума
Линейная система
(фильтр) порядка
P
Оцениваемые параметры:
• Коэффициенты фильтра;
• Мощность шума.
+
Оцениваемый
процесс
Источник
«белого»
шума
Теоретические основы цифровой обработки сигналов. Слайд 144
144. Параметрические методы спектрального оценивания
Модели авторегрессии (АР) и скользящего среднего (СС):b0
+
n i
Z-1
+
b1
x i
a1
Z-1
Z-1
Z-1
H e
j
B e
ap
q
СС:B z bn z
n 0
n
an z
АР: A z 1
n 1
P( )
АР
n 0
p
j
q
Px e j
n
j n
n
j n
b
e
n
2
n 0
p
1 an e j n
n 1
P( )
j
n 1
Z-1
q
j n
b
e
n
A e
1 a e
Z-1
bq
q
P( )
СС
АРСС
Теоретические основы цифровой обработки сигналов. Слайд 145
2
145. Параметрические методы спектрального оценивания
pan rx m n , m 0
n 1
p
rx m an rx m , m 0
n 1
rx m , m 0
Записываем эти уравнения для
rx 0 rx 1
rx 0
rx 1
...
...
rx p rx p 1
0 m p
Связь
параметров
АР – модели и
значений АКФ
процесса
в матричной форме:
... rx p 1
... rx p 1 a1 0
...
... ... ...
...
rx 0 a p 0
Нормальное
уравнение
Юла-Уолкера
для АР –
процесса
Теоретические основы цифровой обработки сигналов. Слайд 146
146. Параметрические методы спектрального оценивания
Методика построения оценки СПМ для АР- процесса:• Рассчитываются значения АКФ : rx 0 , rx 1 ,...rx m ,...rx p ;
• Решается уравнение Юла-Уолкера относительно параметров
АР- модели a1 , a2 ,...a p и спектральной плотности
• Вычисляется оценка СПМ:
Px e
j
1
p
1 an e j n
2
n 1
Теоретические основы цифровой обработки сигналов. Слайд 147
;
147. Параметрические методы спектрального оценивания
Взаимосвязь классических и параметрических методов оценки СПМ.rx(m)
Px(k)
истинная
СПН
m
измеренные
значения
rx(m)
истинные значения
Px(k)
окно
нулевая
экстраполяция
m
rx(m)
Px(k)
m
затухающая
экстраполяция
коррелограммная оценка
АР оценка СПМ
затухающая экстраполяция
Теоретические основы цифровой обработки сигналов. Слайд 148
148. Параметрические методы спектрального оценивания
Преимущества параметрических методов:• высокое разрешение, что соответствует «длинной» АКФ;
• отсутствие боковых лепестков весовой функции «окна».
Недостатки параметрических методов:
• неопределен выбор порядка модели;
• зависимость разрешения от отношения сигнал/шум
1.03
Формула Марпла
;
f
T p Q 1
0.31
• возможная потеря устойчивости.
с / ш = 30 дБ
с / ш = 20 дБ
с / ш = 10 дБ
Теоретические основы цифровой обработки сигналов. Слайд 149
149. Параметрические методы спектрального оценивания
Сводная таблицапараметрических
Общие
свойства методов оценки
Недостатки
Условия
несингулярности
Преимущества
СПМ
КовариациМодифиц.
Ковариационн
Модифиц.
ЮлаЮлаБерга
Метод
Берга
КовариациМодифиц.
Юлаонный
ковариац.
ый
ковариац.
Метод
Берга
КовариациМодифициУолкера
Уолкера
ЮлаМетод
Характеристики
Метод
Берга
онный
ковариац.
Уолкера
онный
Уолкера
Не использует
Не использует
Нерованный
использует
Использует
Расположение
Может
Может
Работает
Берга
Общие
свойства
ковариациВысокое
Разрешение
Высокоек
Для длинных
взвешивание
взвешивание
взвешивание
взвешивание
пиков
сильно
приводить
к
приводить
относительно
разрешение
выше,
чем у
разрешение
блоков
онный
данных
данных
данных
данных
зависит
отдля неустойчивым
неустойчивым
плохо
для
Ковариационный
Преимущества
короткой длины
Юла-Уолкера
для
короткой
данных
функцией
«окна»
функцией
функцией
функцией
начальных
фаз
моделям
моделям
коротких
Порядок
должен
Порядок
блока -данных
при«окна»
коротких
длины
блока
разрешение
«окна»
«окна»
блоков
Модифицированный
Недостатки
быть
меньше,
быть
блоках
данных должен
данных
такое
же, как у
данных
либо равен
меньше, либо
других
ковариационный
Подвержен
Смещение
Расположение
Смещение
Минимальная
Минимальная
Минимальная
Минимальная
половине
равен 2/3
методов
расщеплению
частот
оценок
пиков
слегка
частот
оценок
СКО
СКО
СКО
СКО
размера кадра
размера
кадра
Юла-Уолкера
Условия
несингулярности
Всегда
Работоспособен
РаботоспосоВсегда
спектральных
синусоид
зависит
синусоид в
предсказания
предсказания
предсказания
предсказания
данных в
данныхот
устойчивые
для
P
чистых
бен
для
P
устойчивые
линий
при и
шуме
начальных
шуме
«вперед»
«вперед»
«вперед»
и
«вперед»
модели
гармоник в
чистых
модели
высоком
порядке
фаз
«назад»
с
«назад».
шуме
гармоник в
модели
ограничением
шуме
алгоритма
Смещение
частот
Наименьшее
ДурбинаНе
подвержен
оценок
синусоид
смещение
Левинсона
расщеплению
в шуме
частот
оценок
спектральных
синусоид в
линий
шуме
Теоретические основы цифровой обработки сигналов. Слайд 150


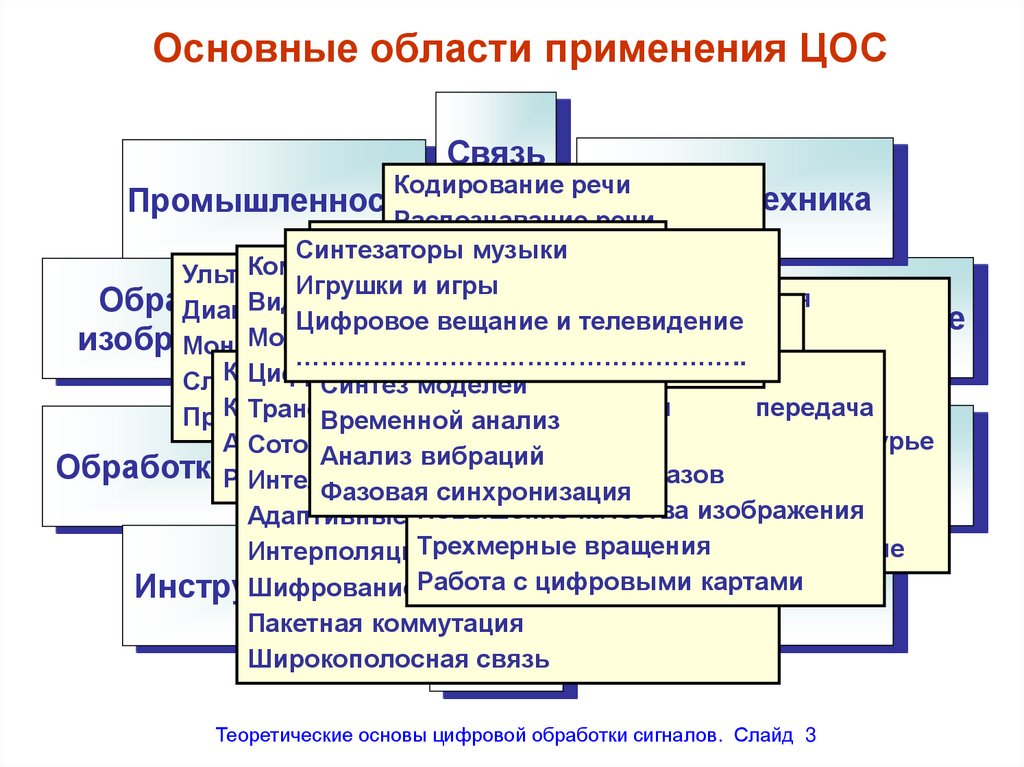

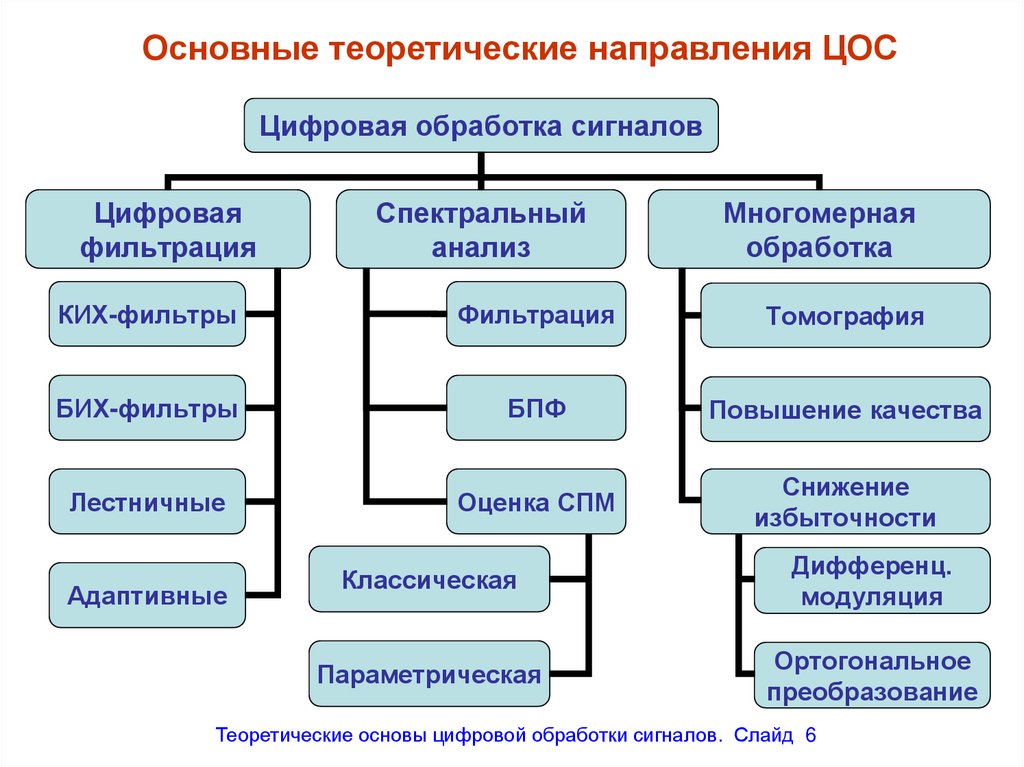
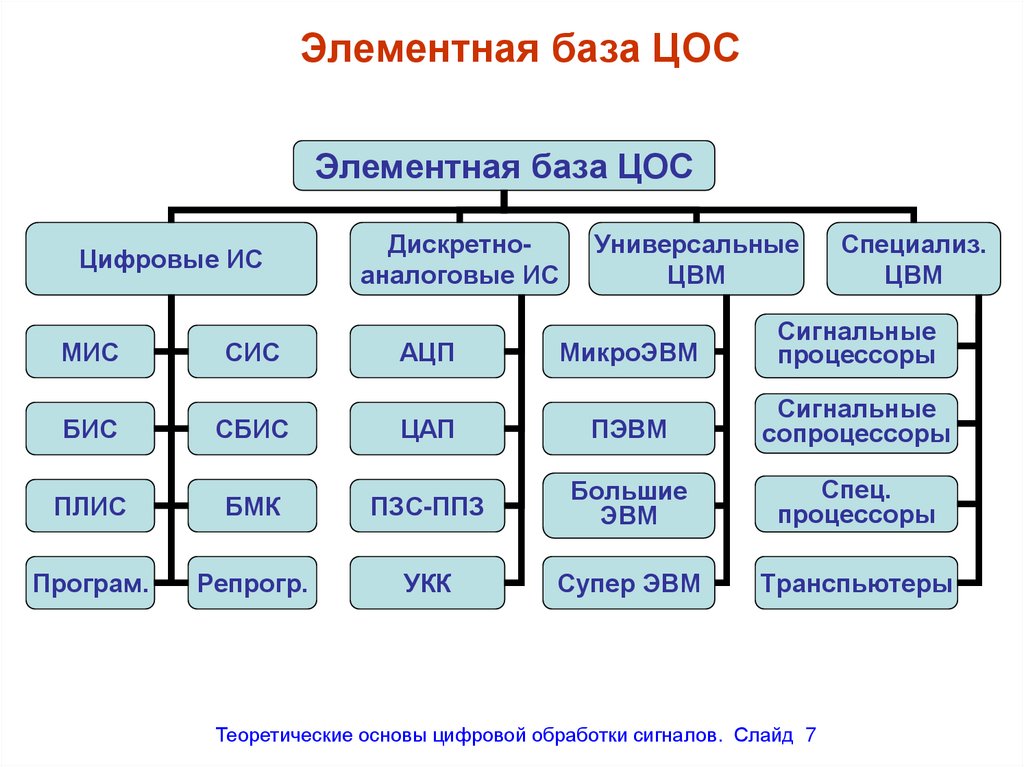


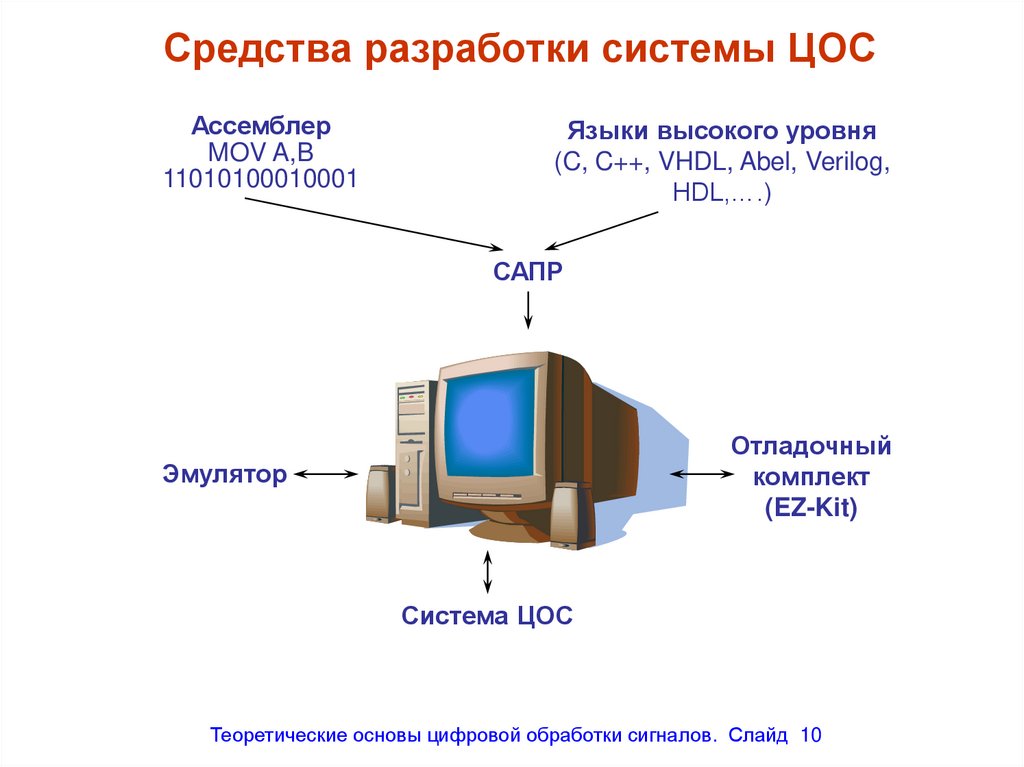
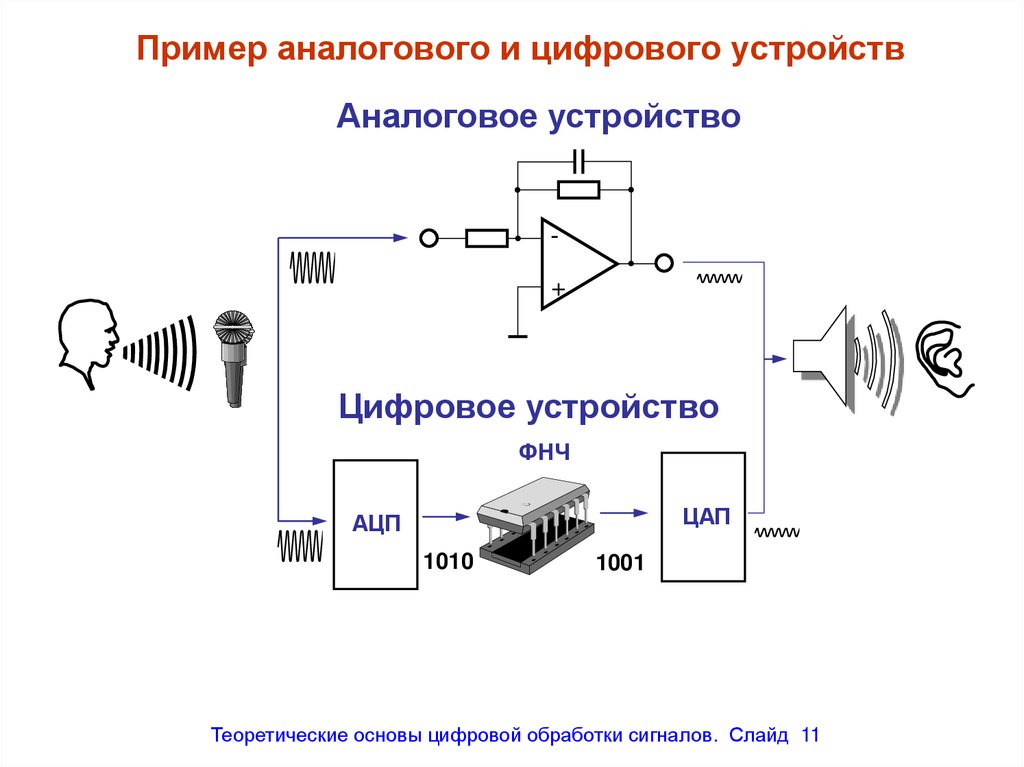

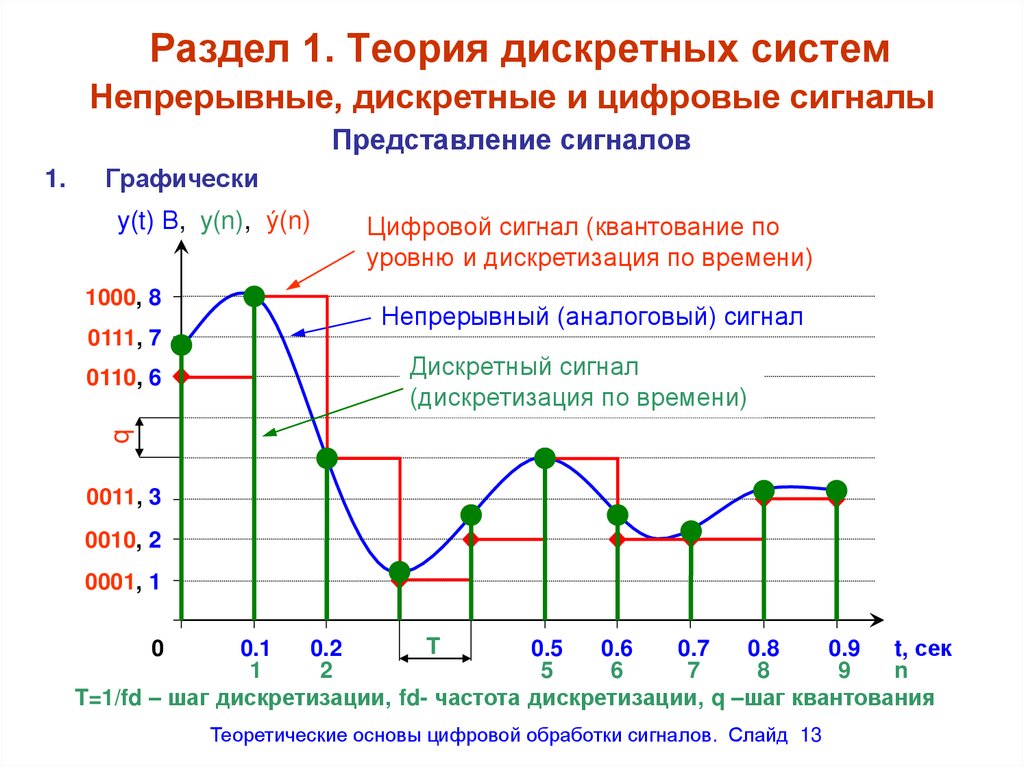
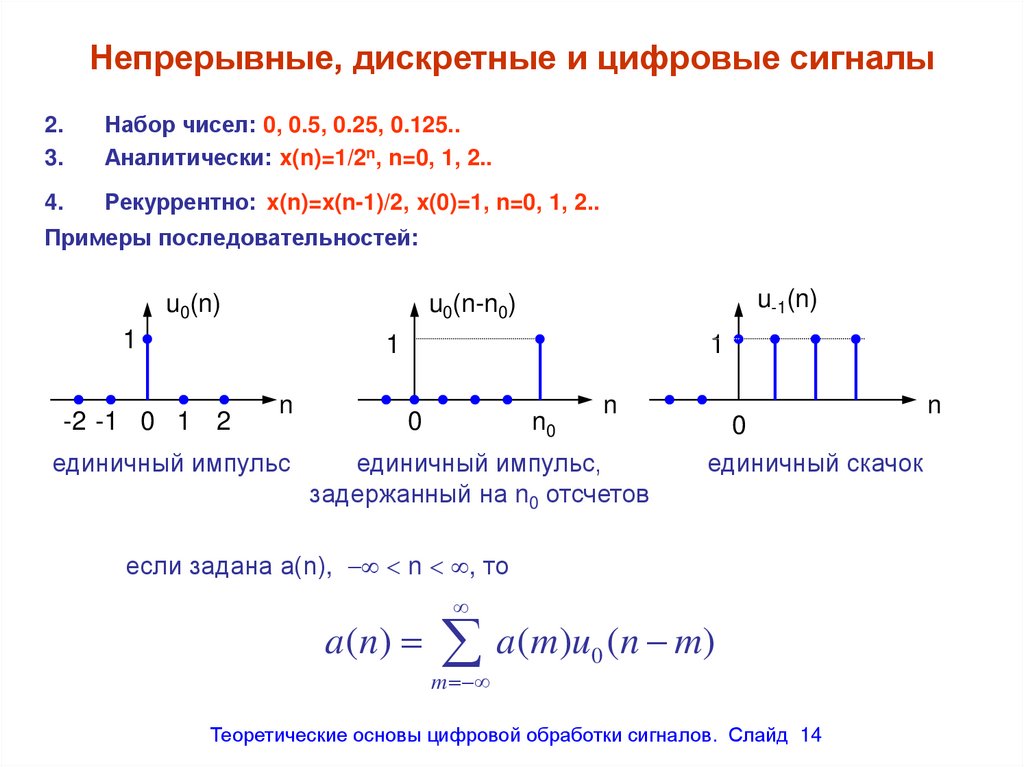
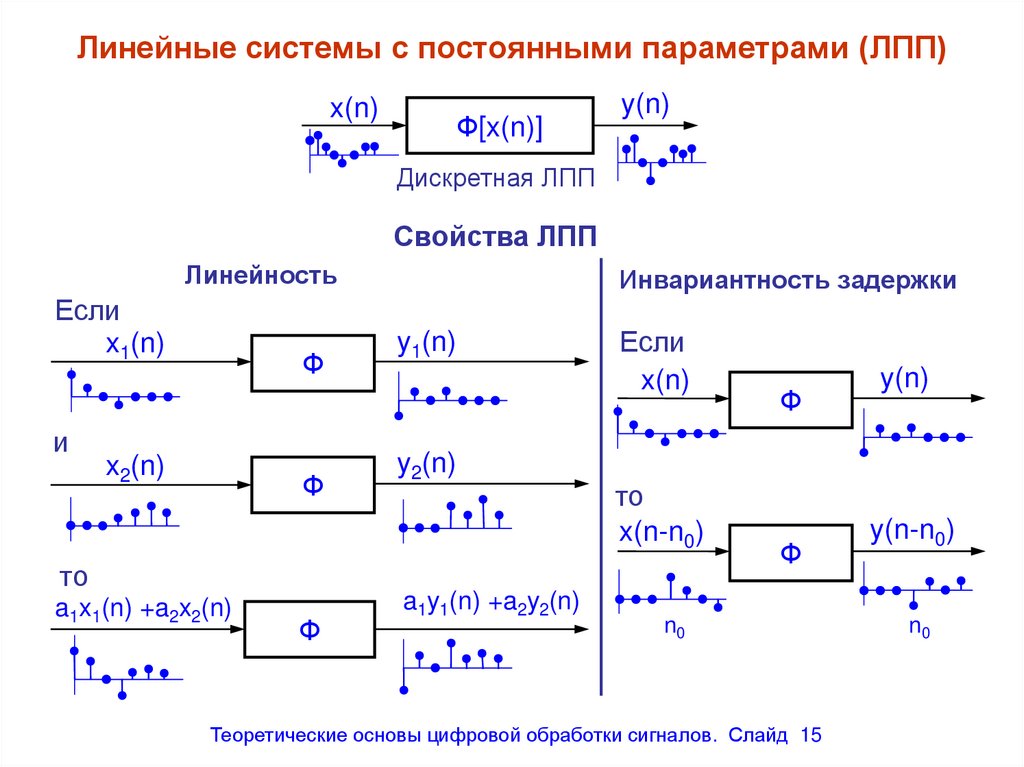
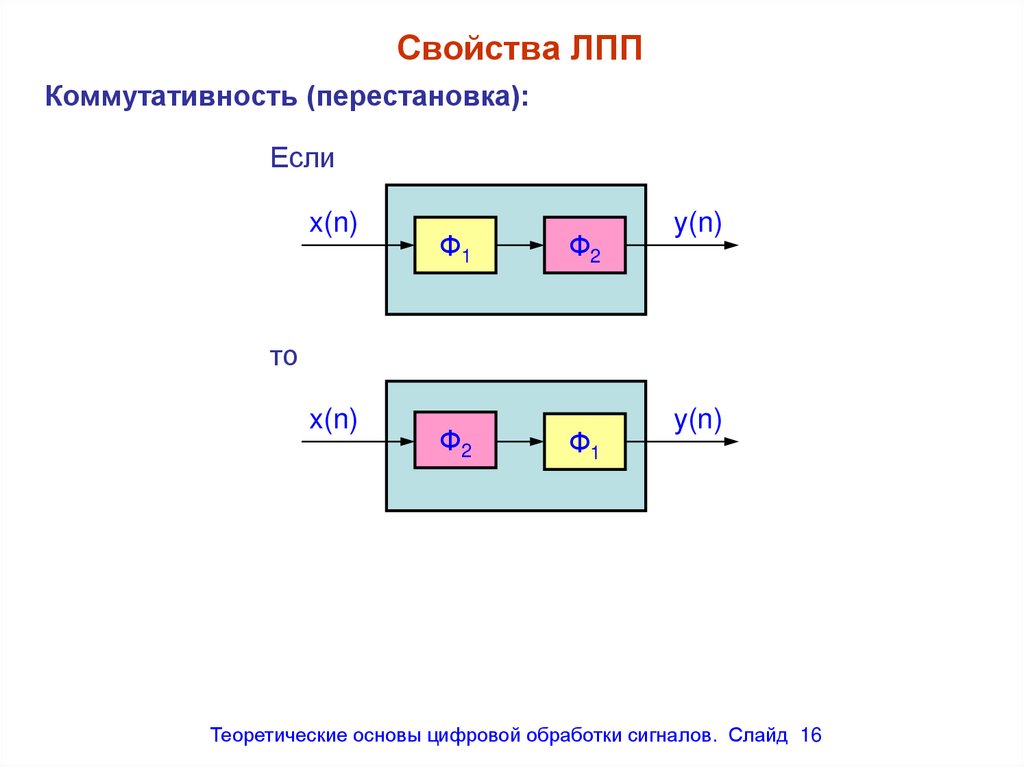
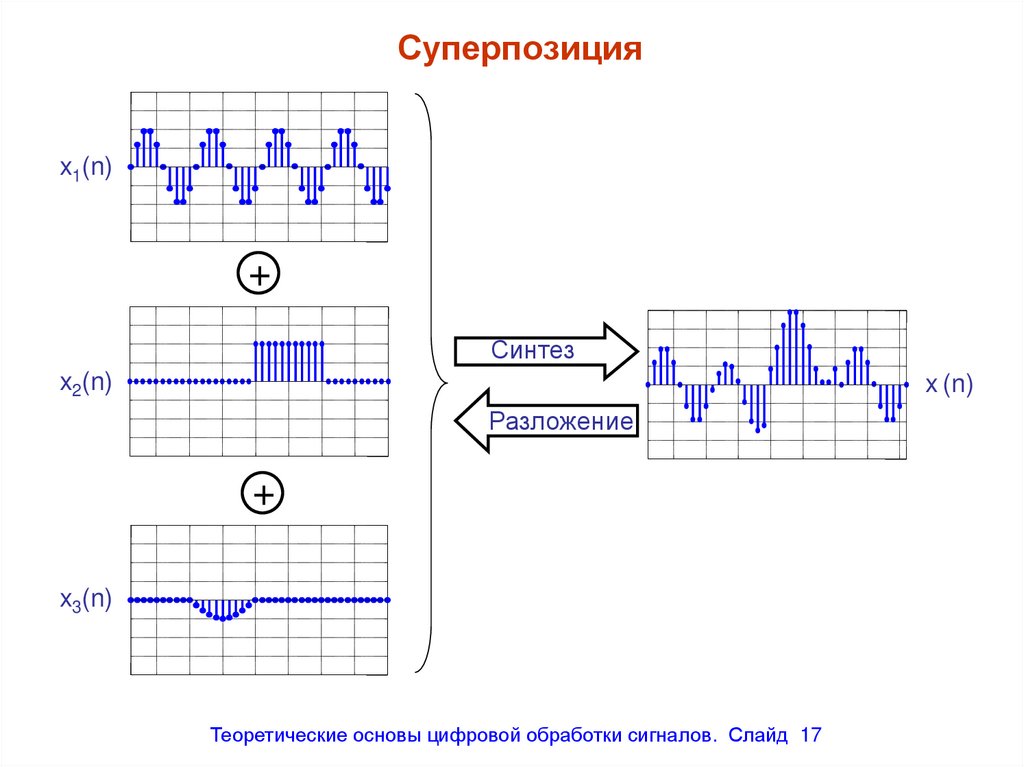
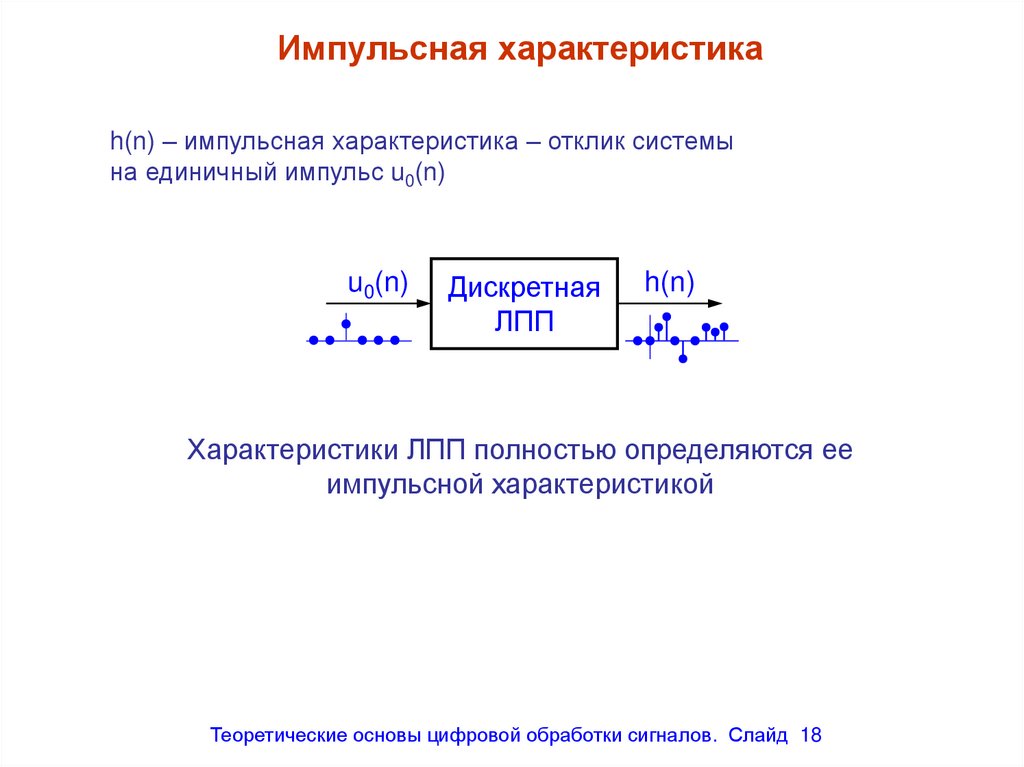
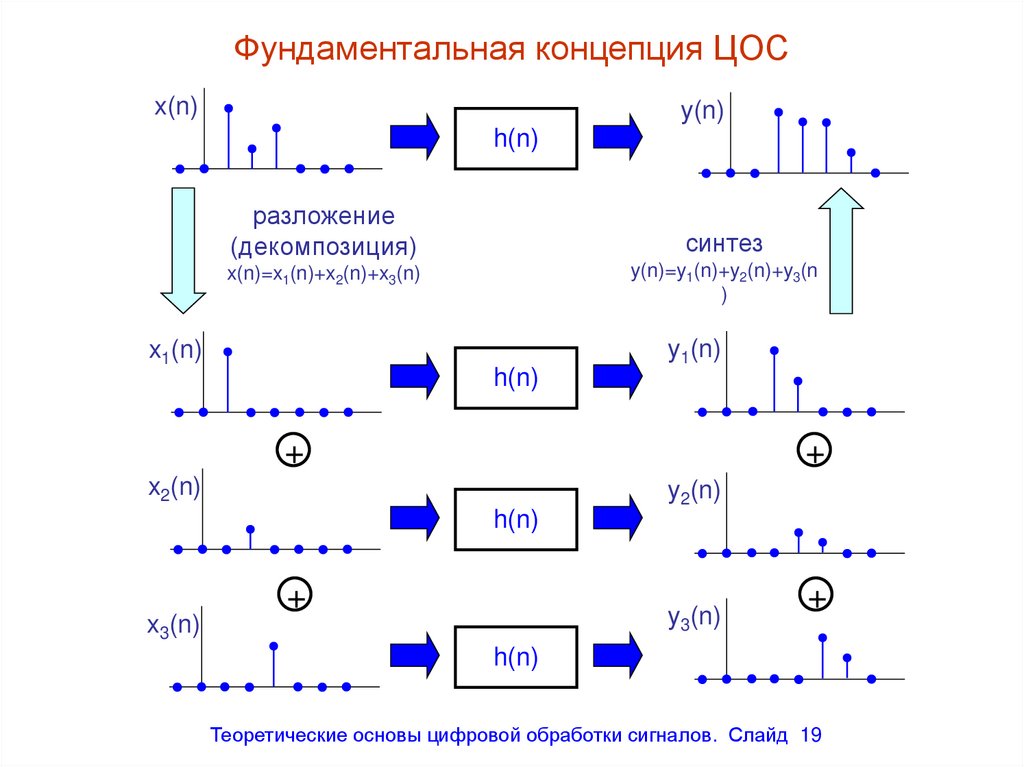
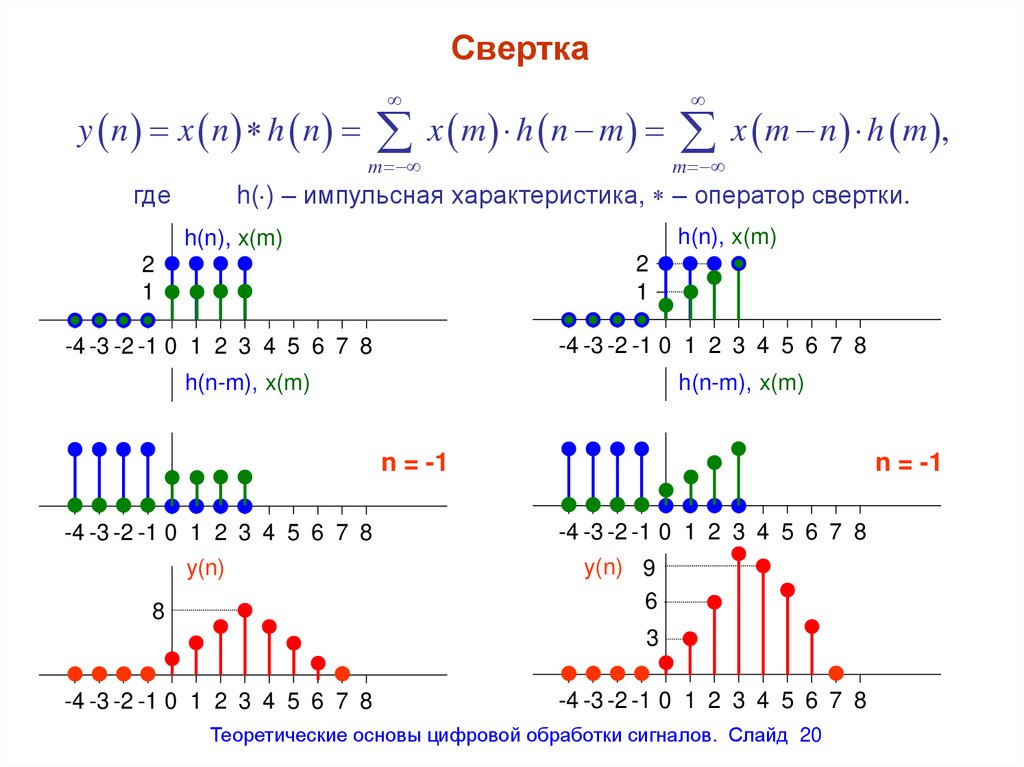
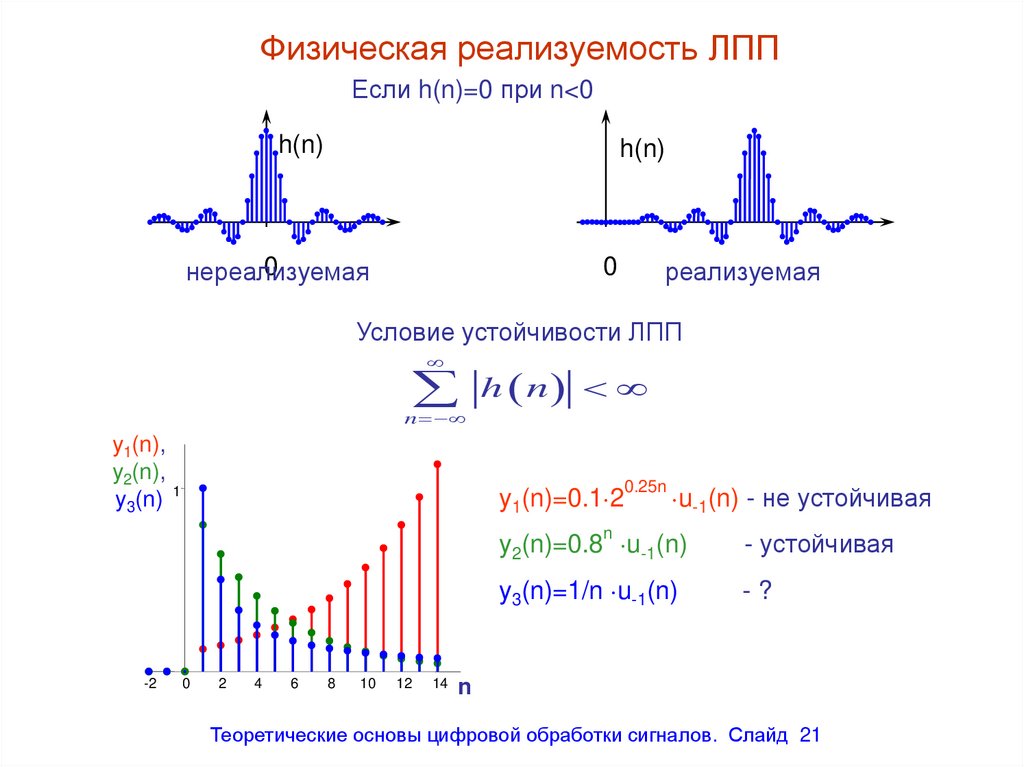
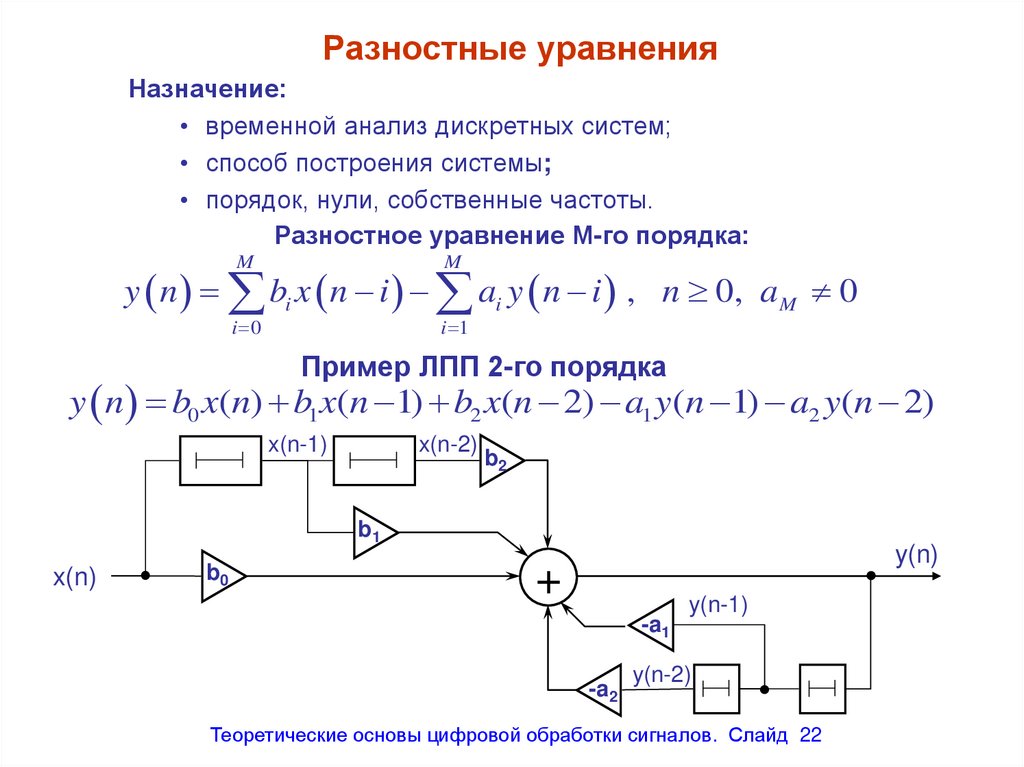



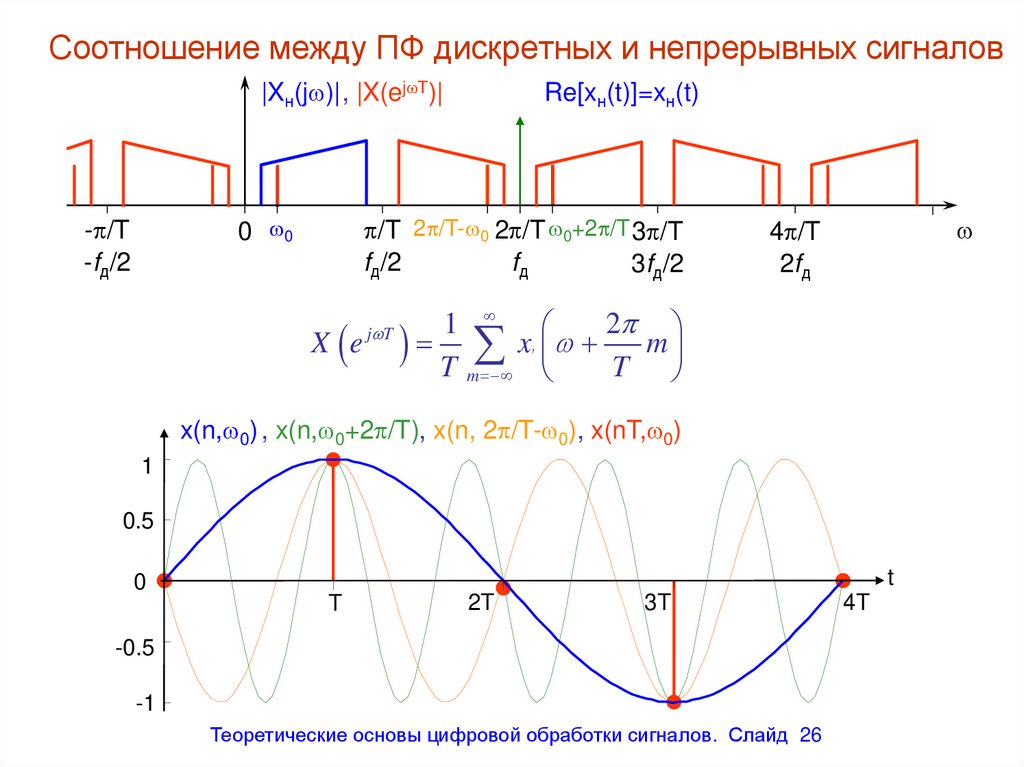
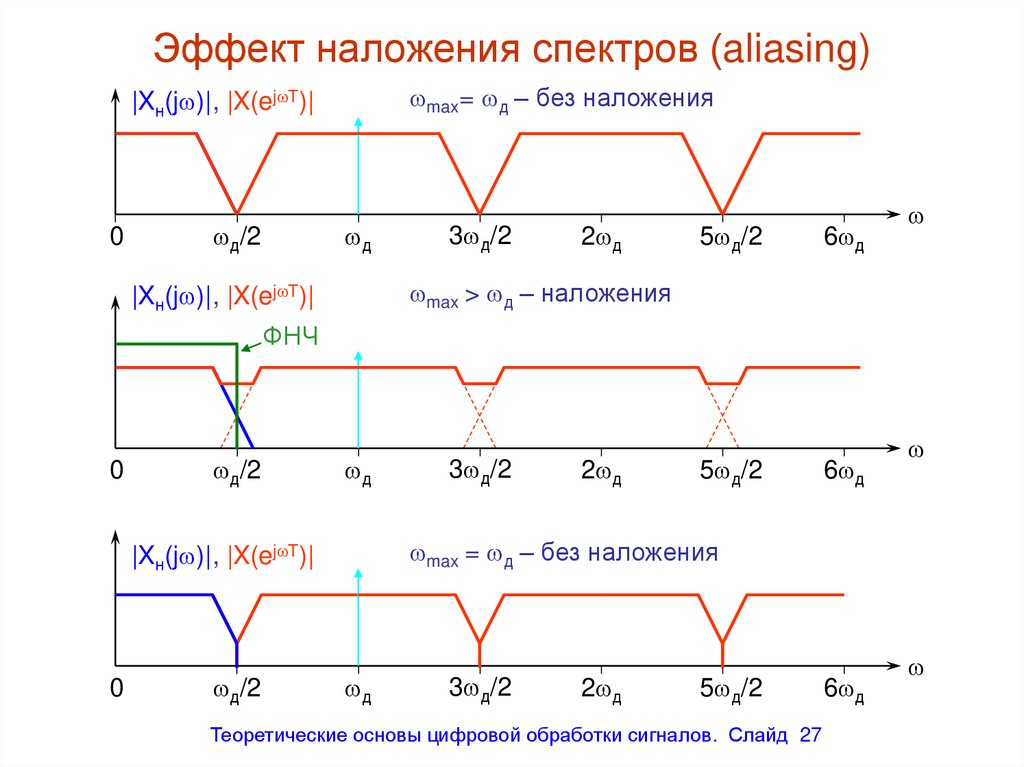



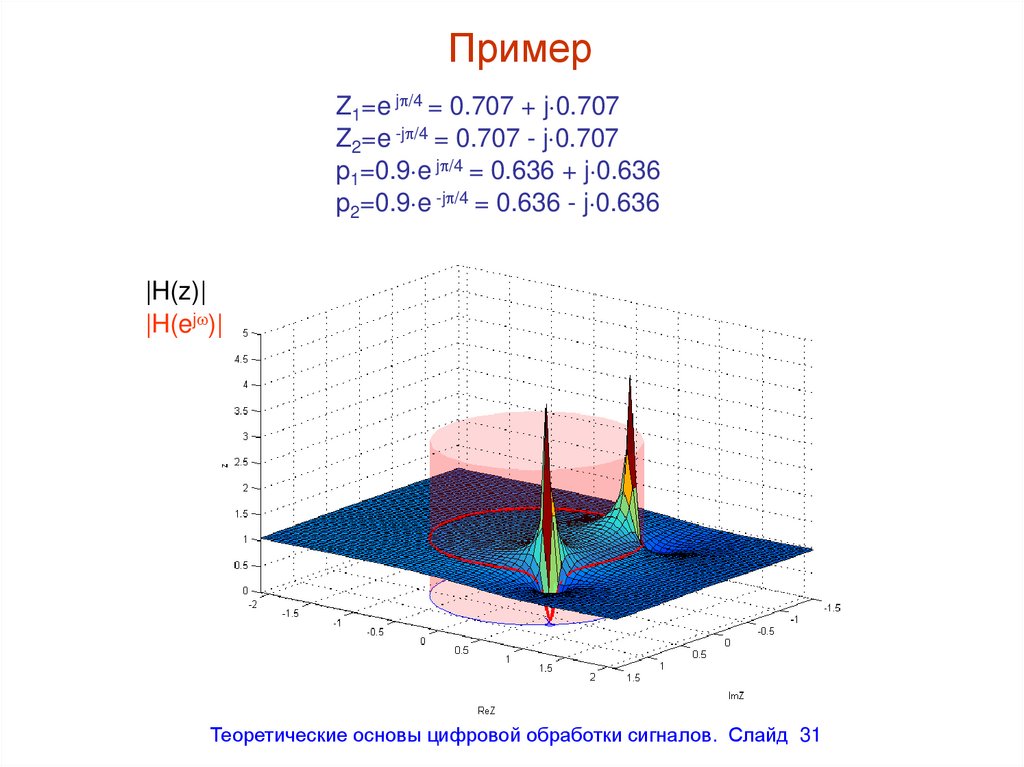









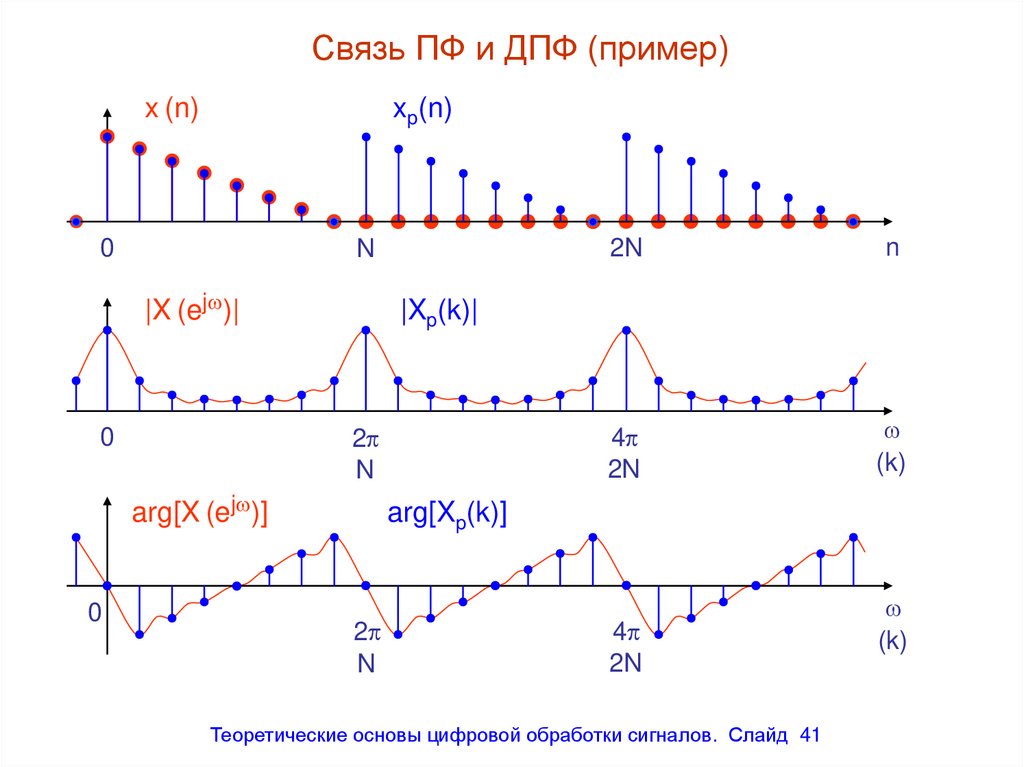




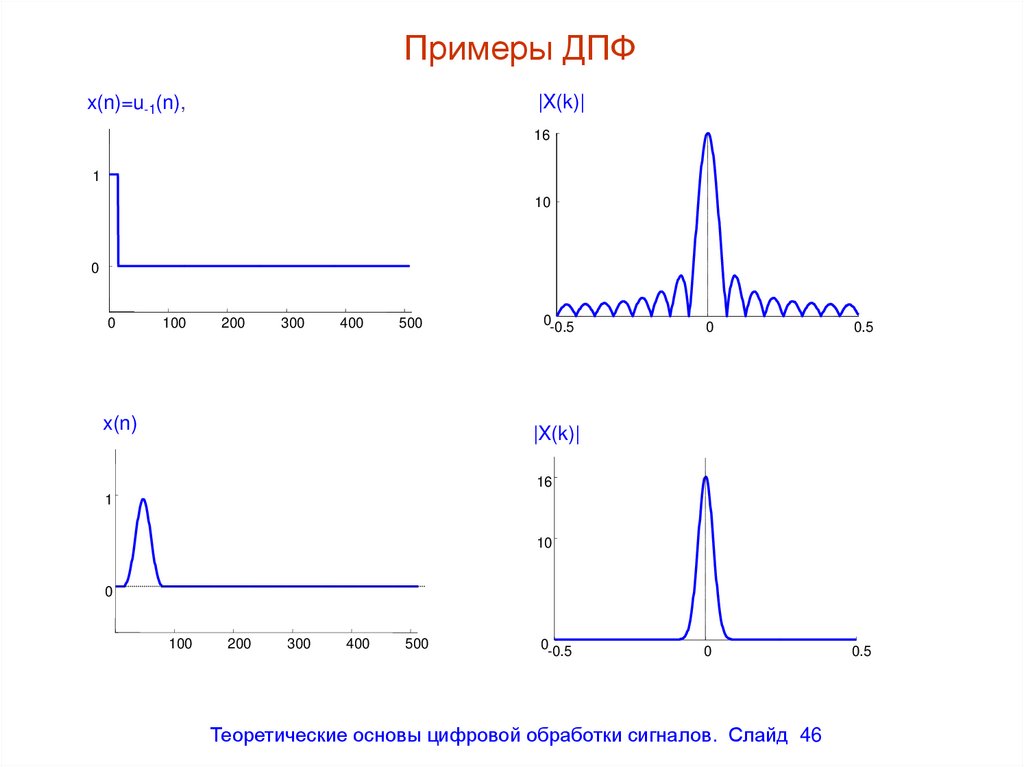

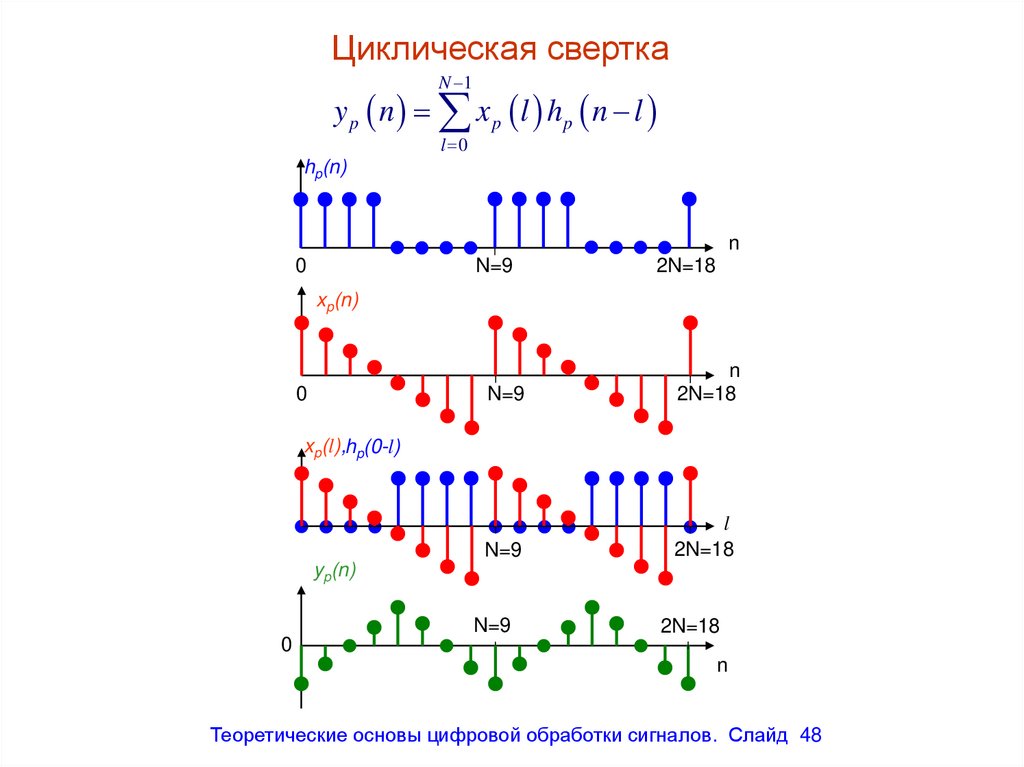
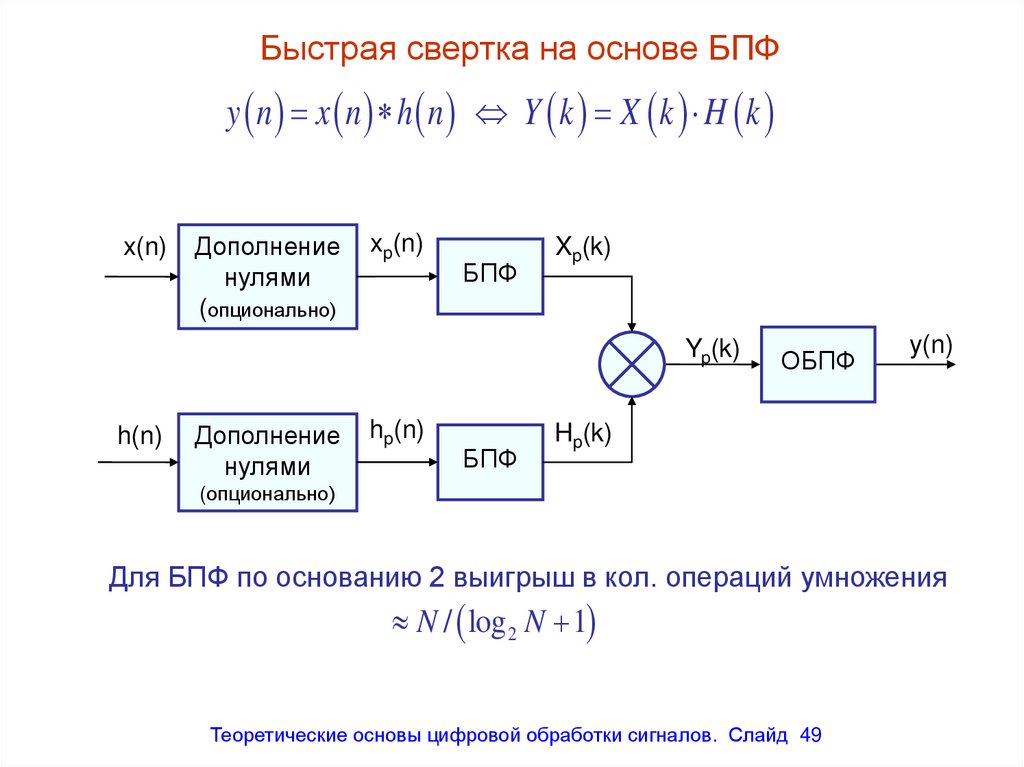
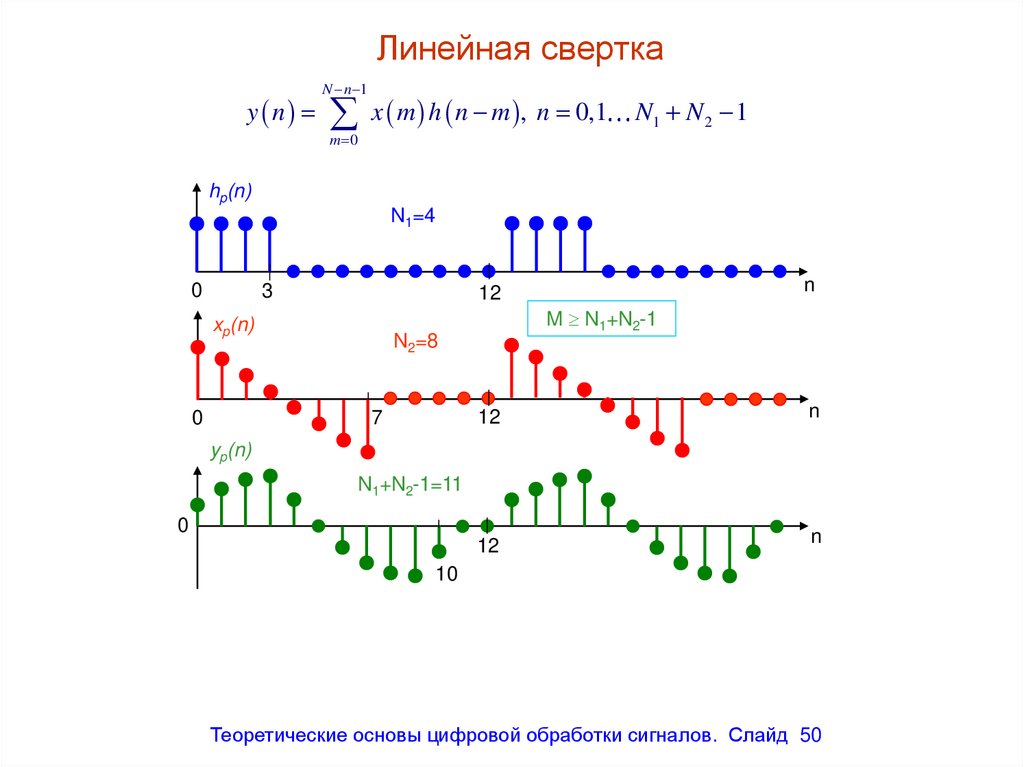
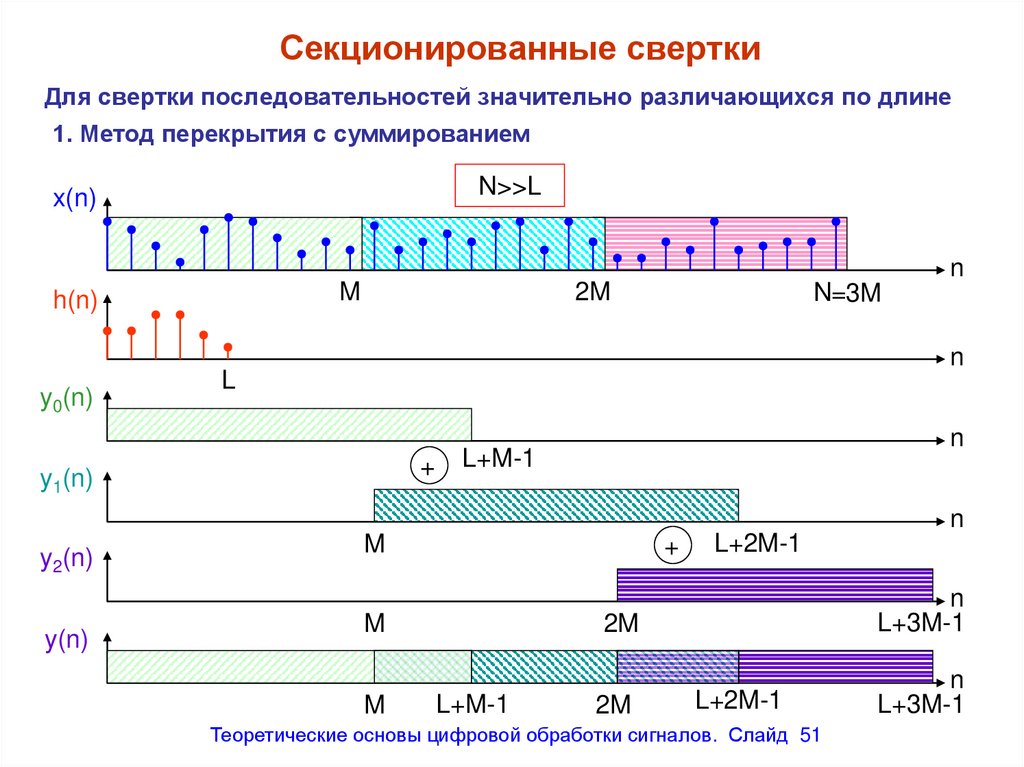
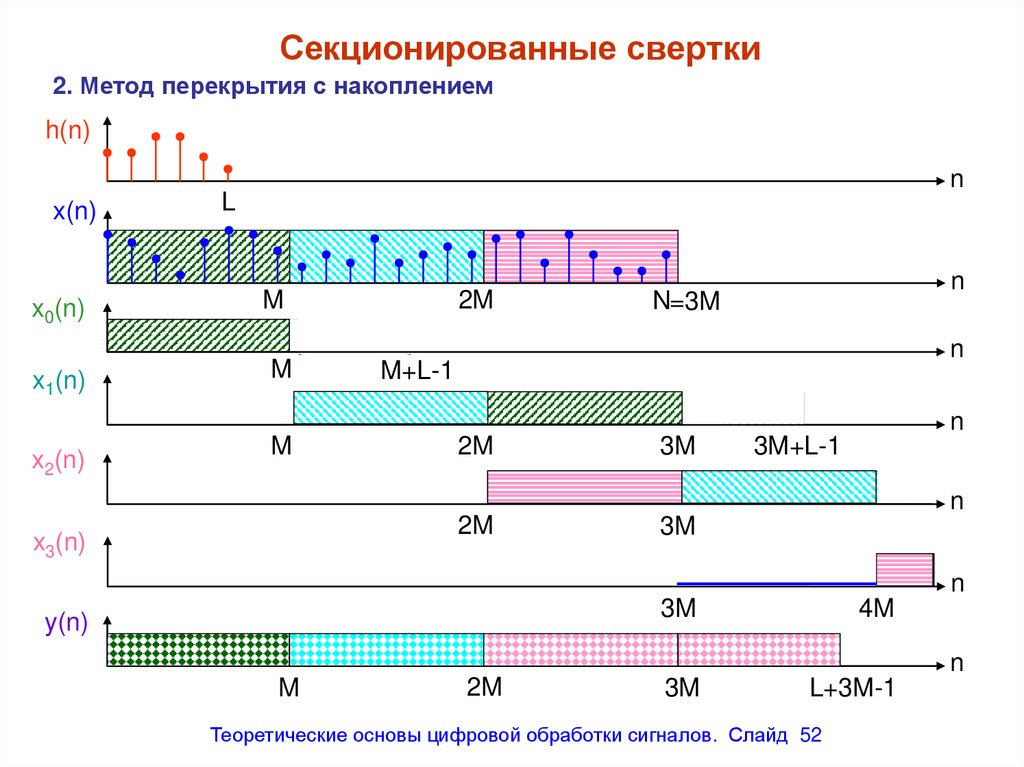

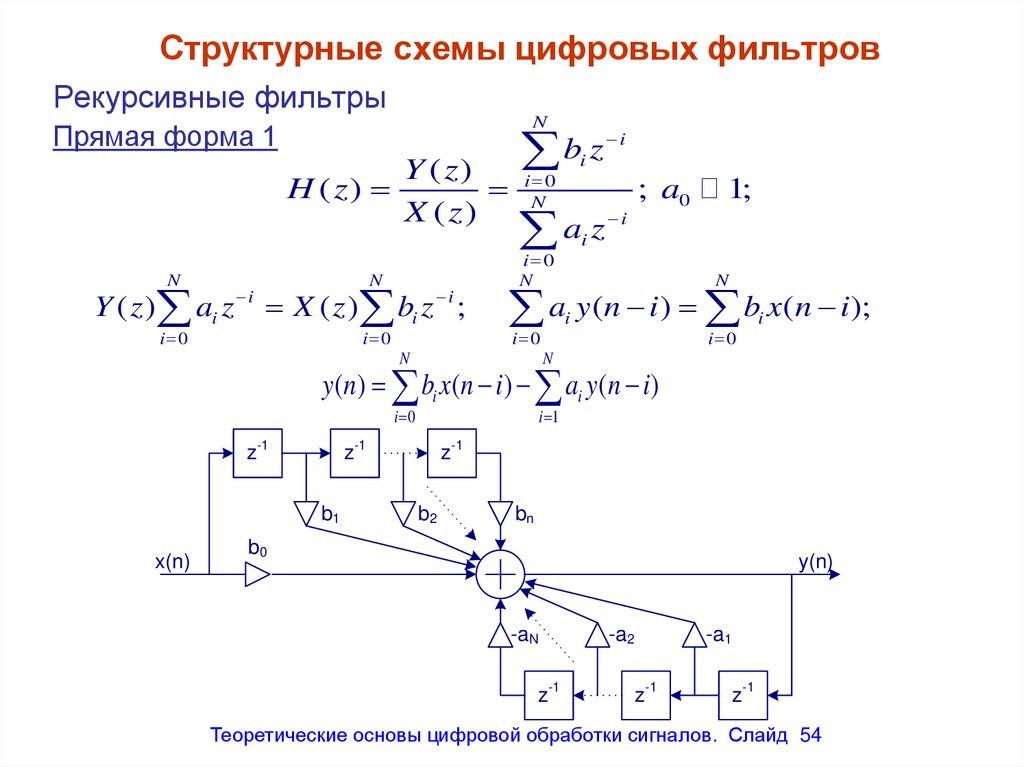
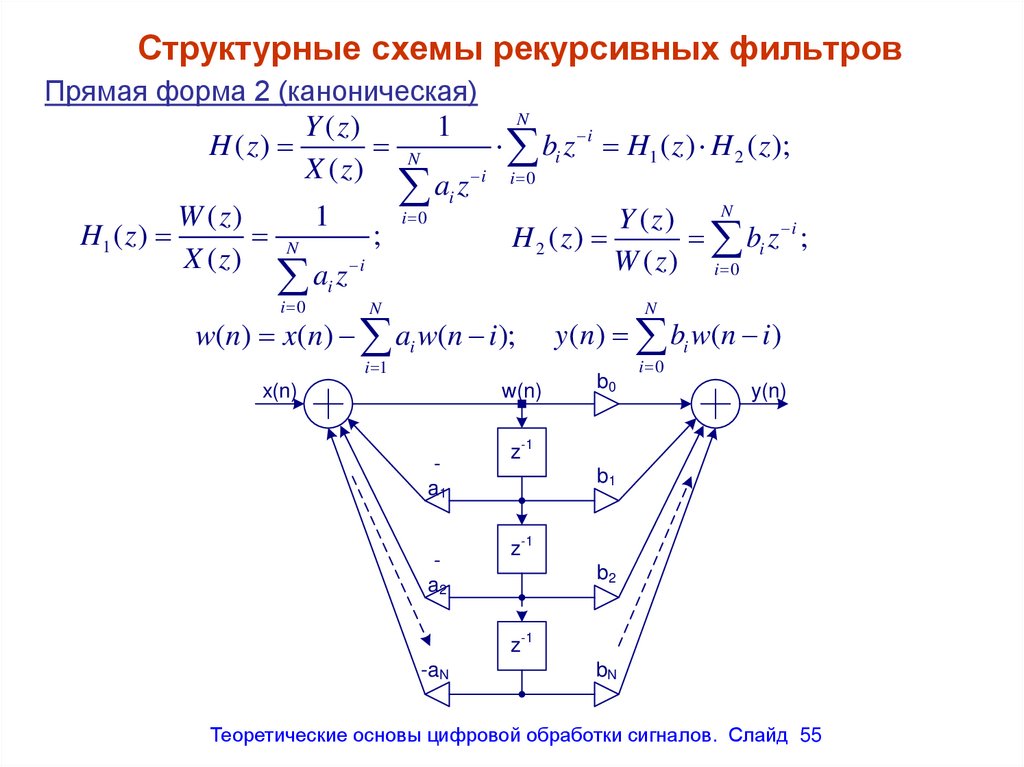
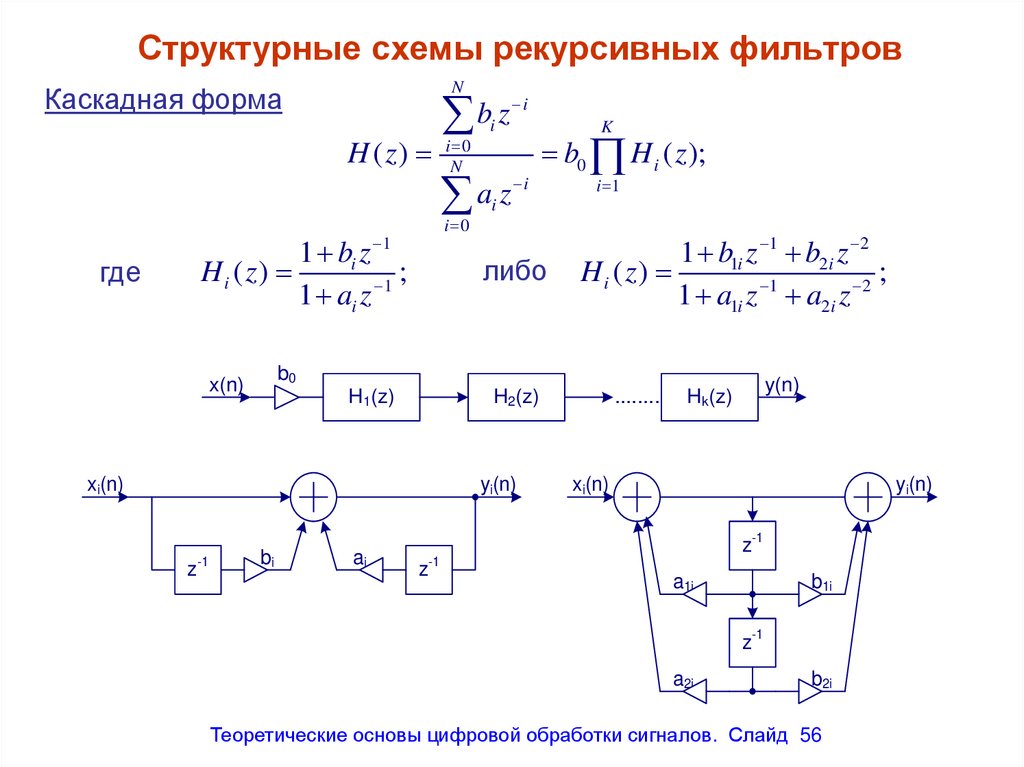
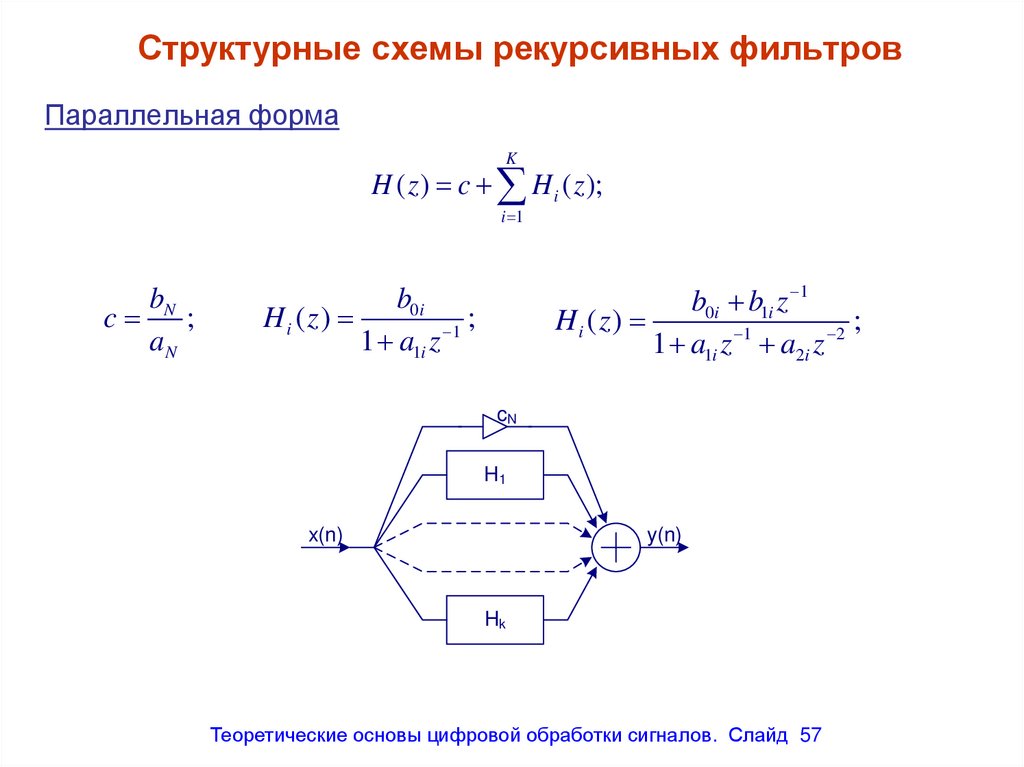
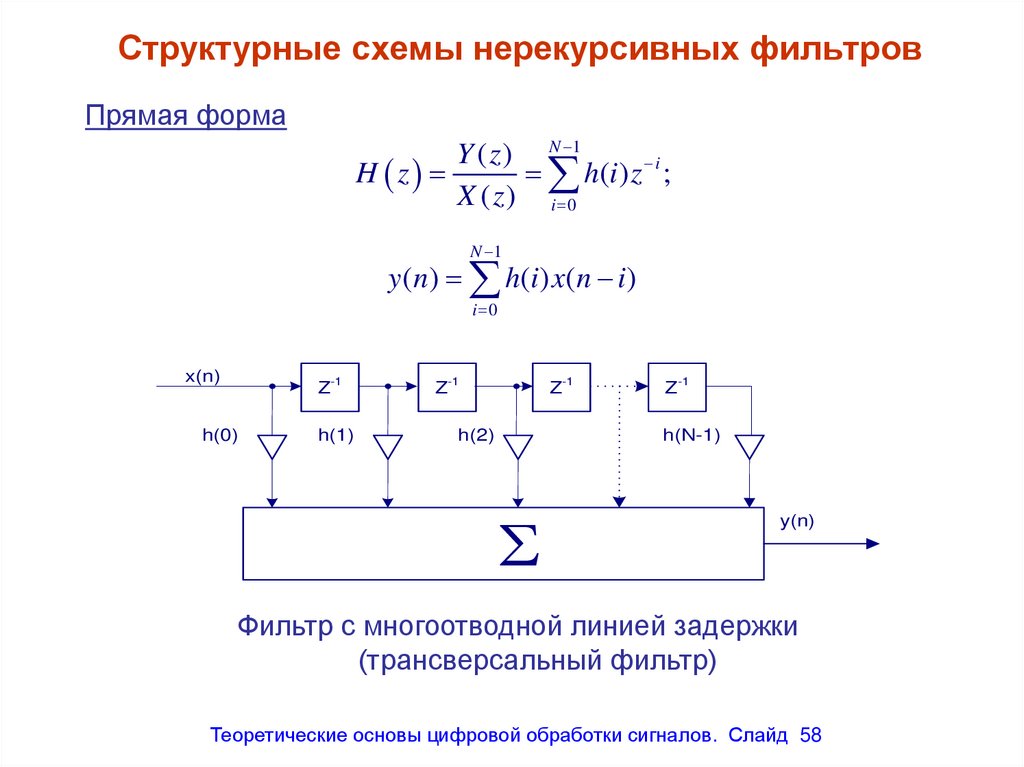
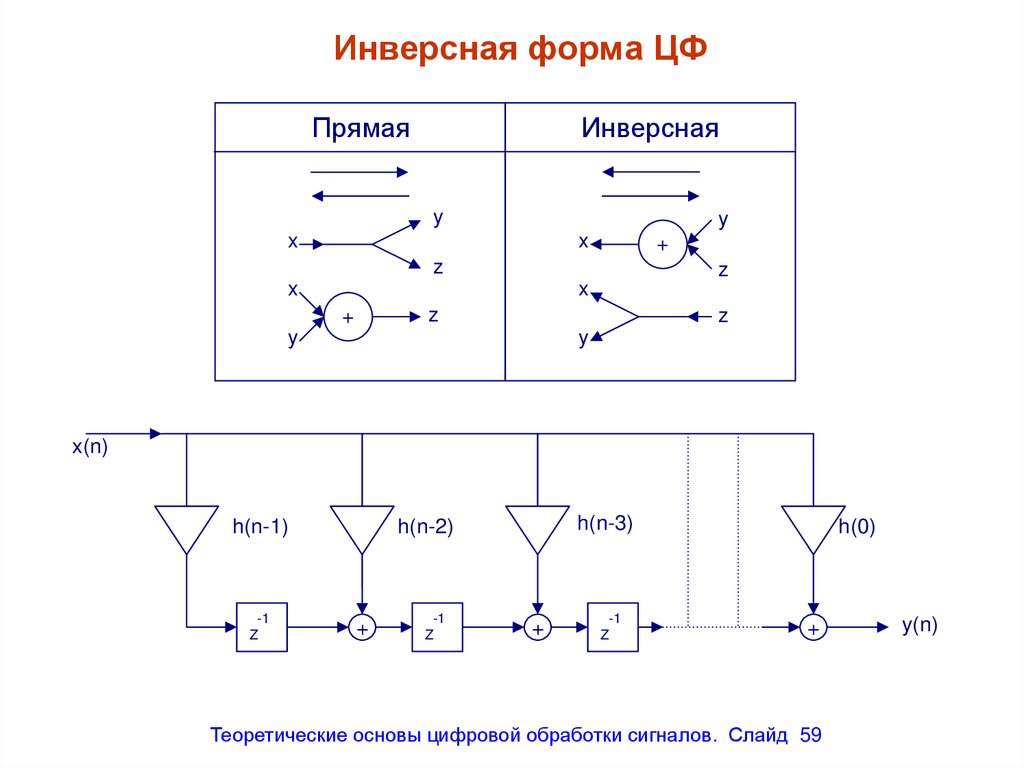

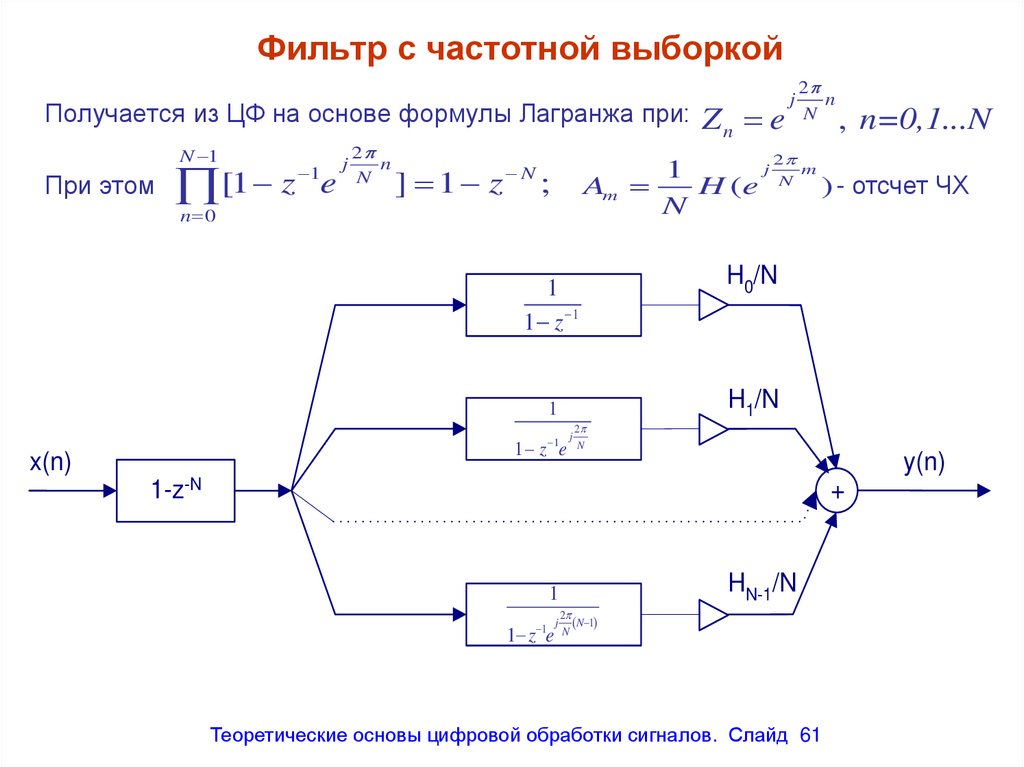


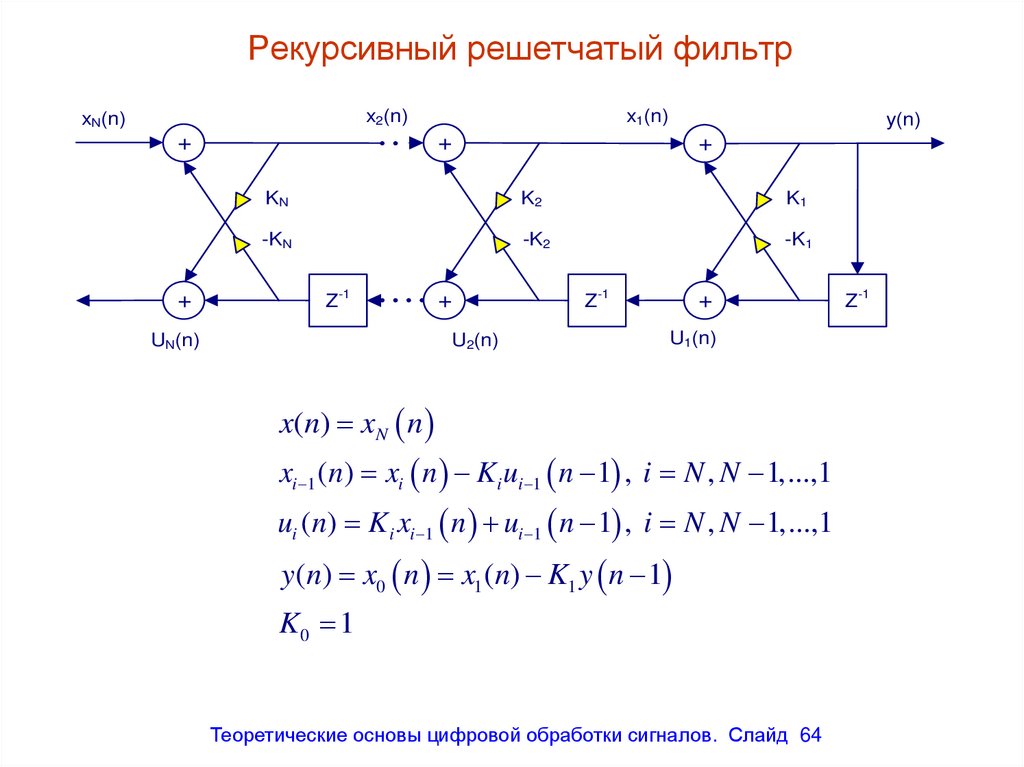


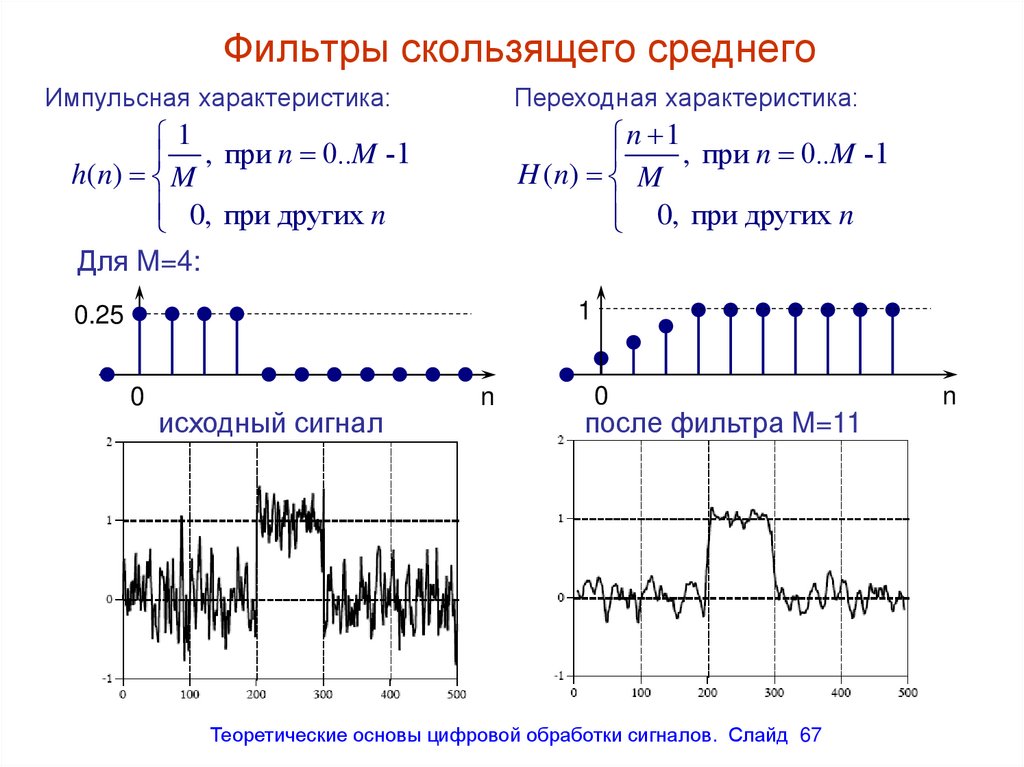
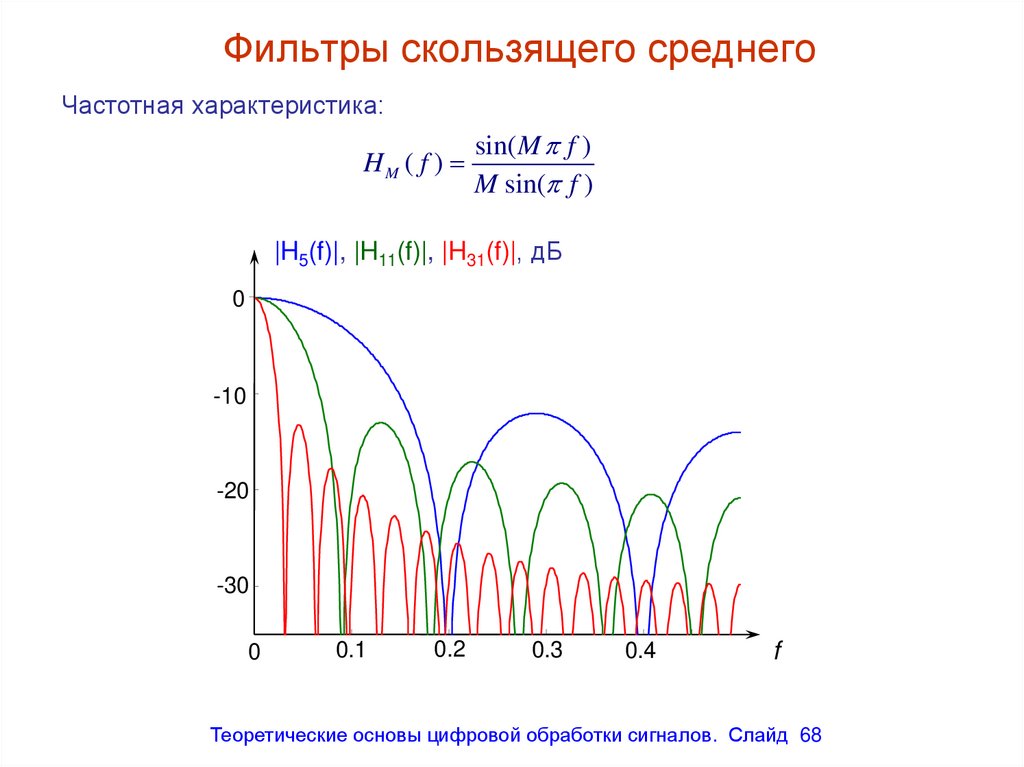

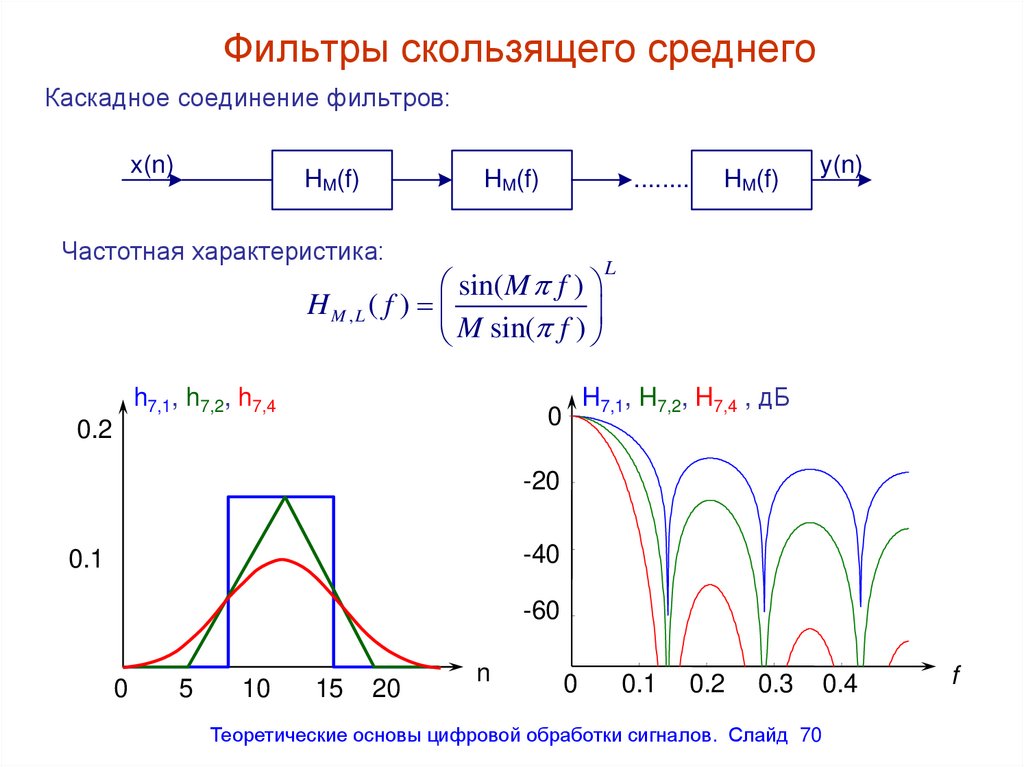



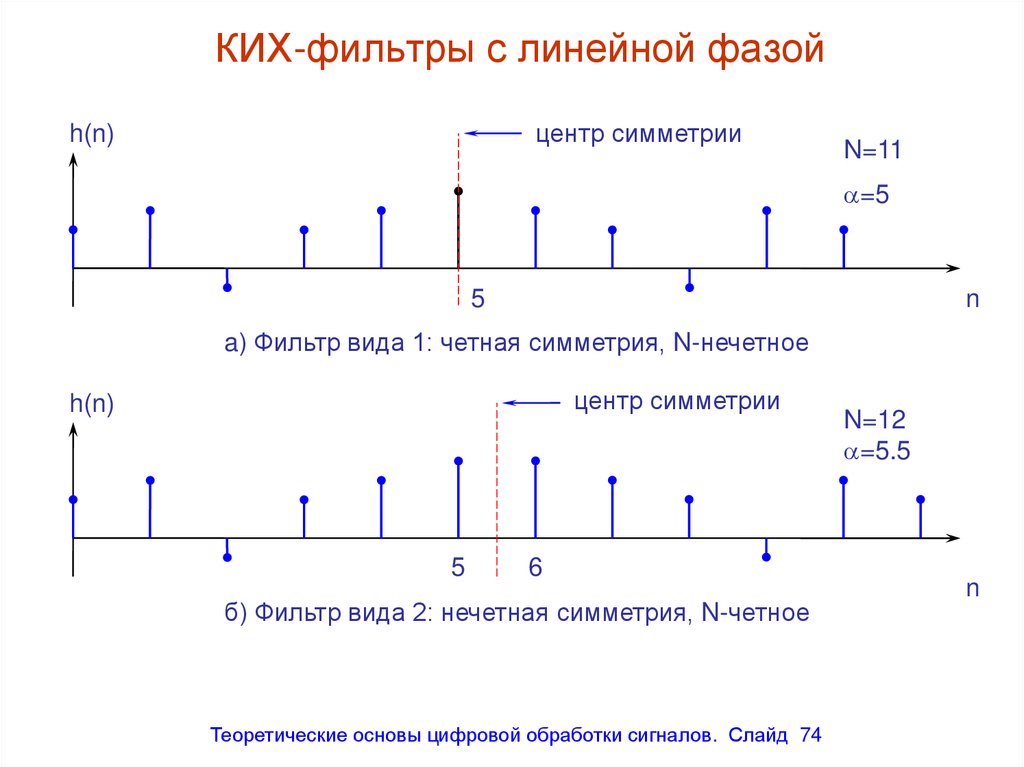

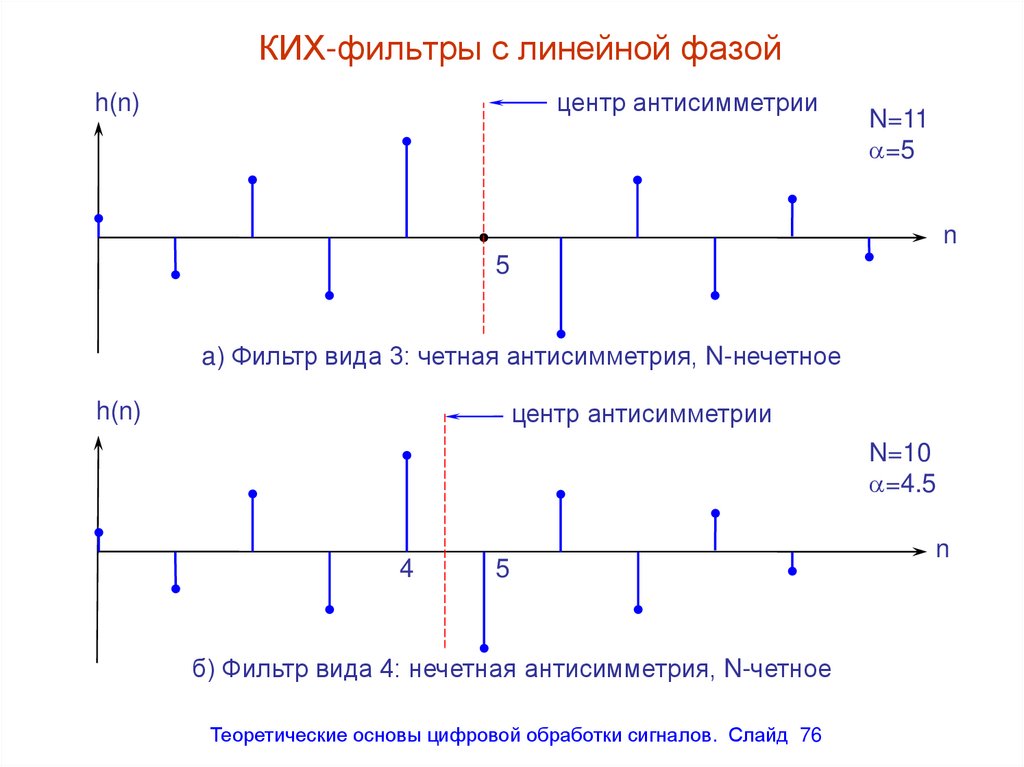
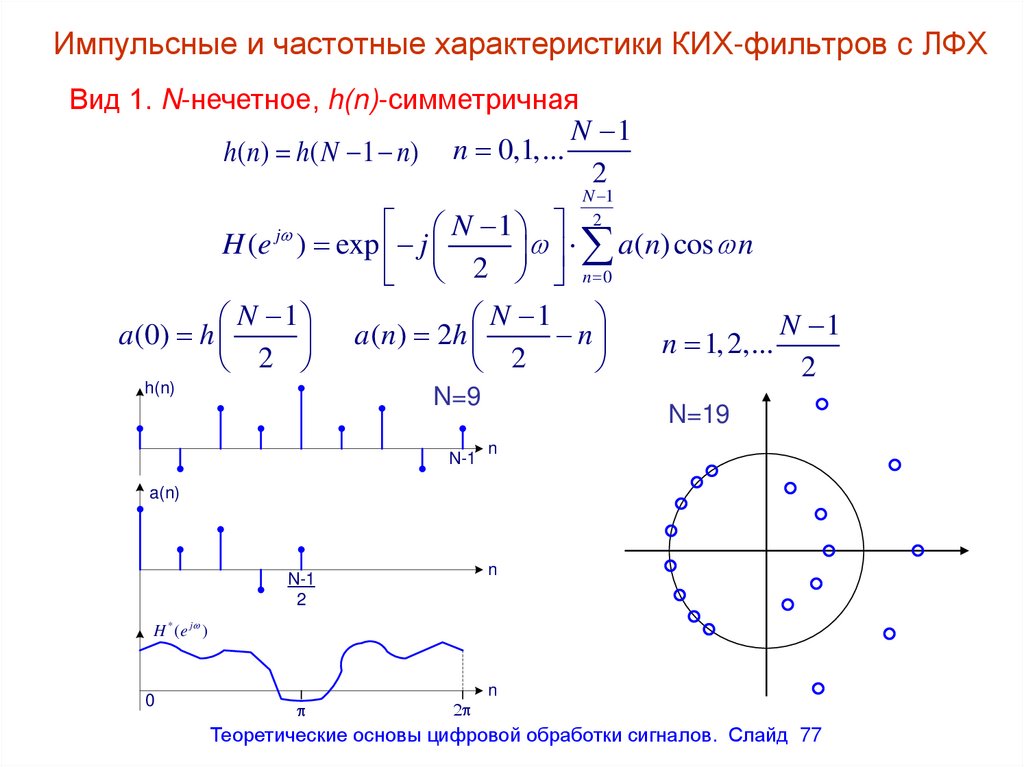
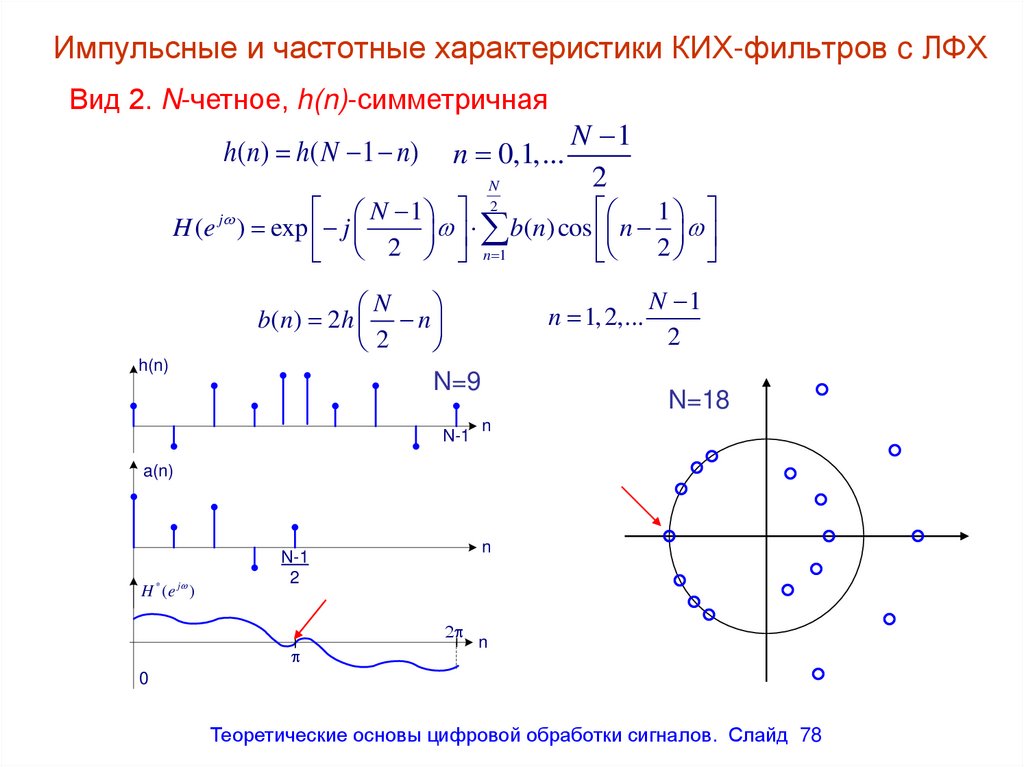


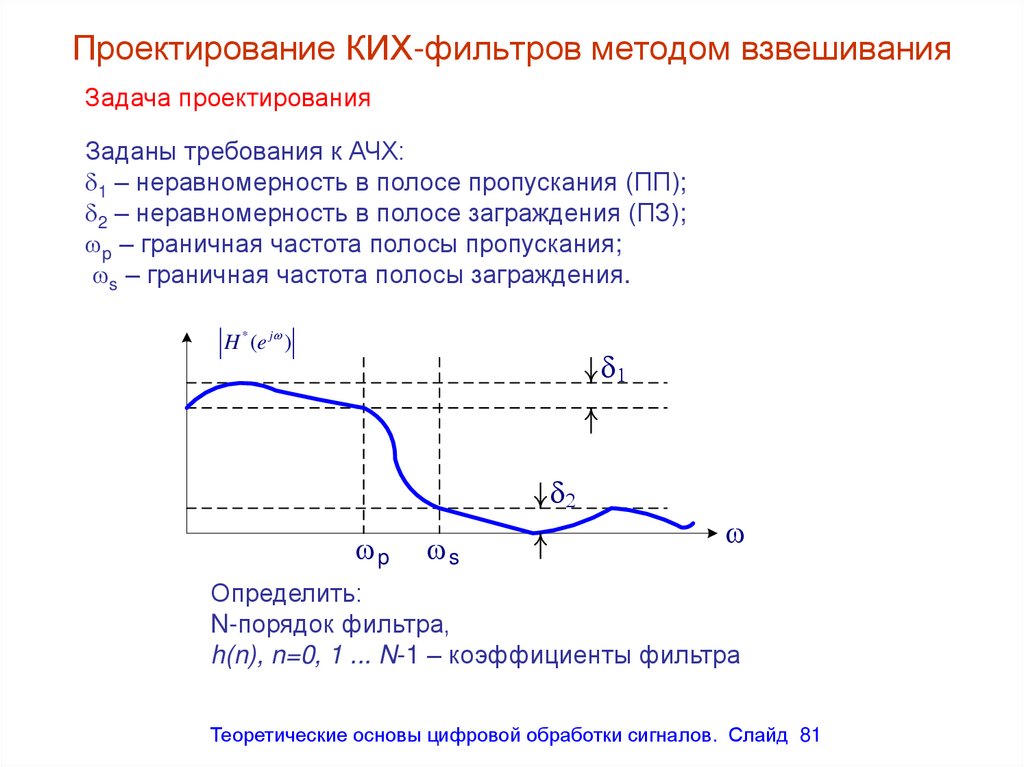
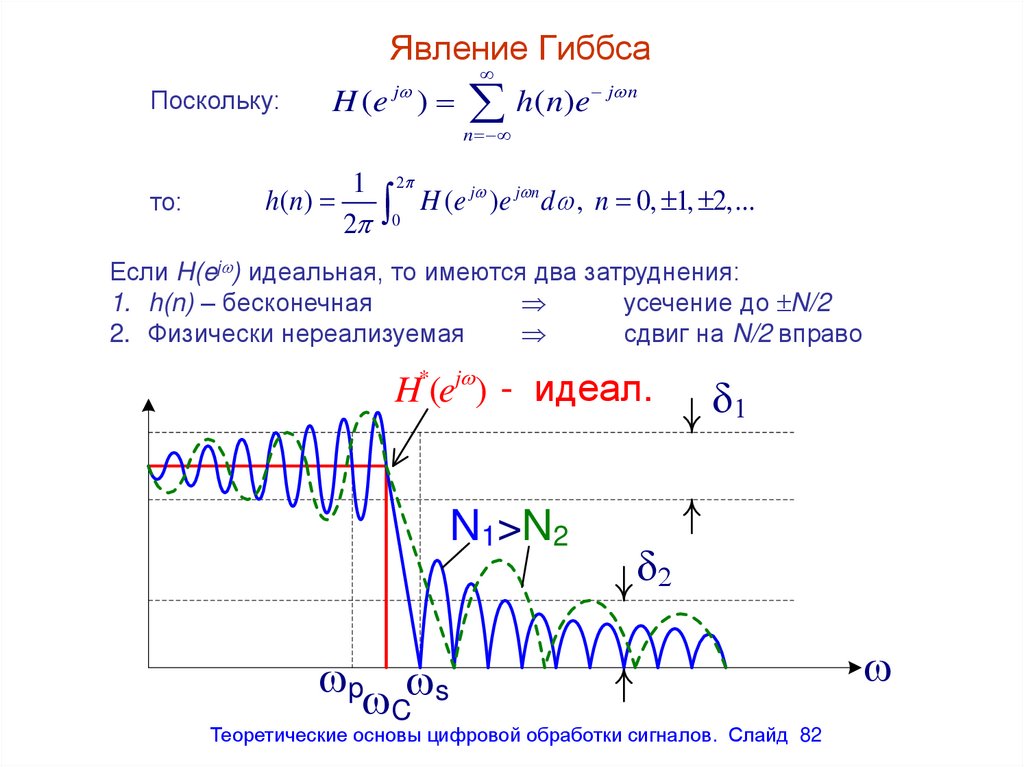

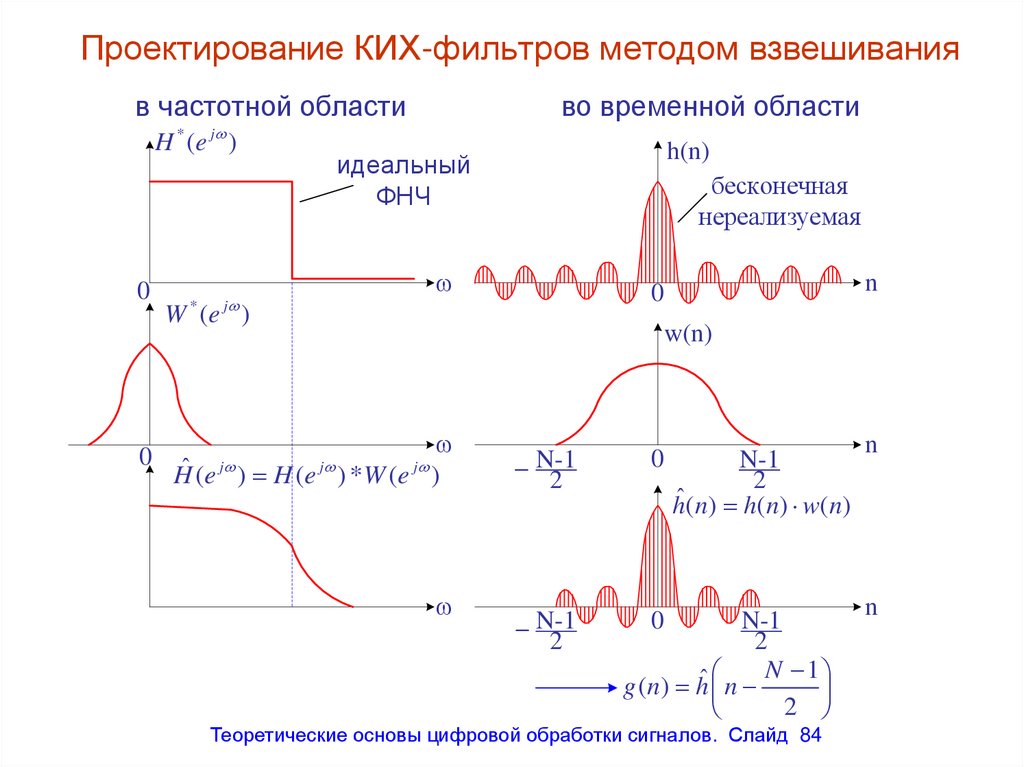

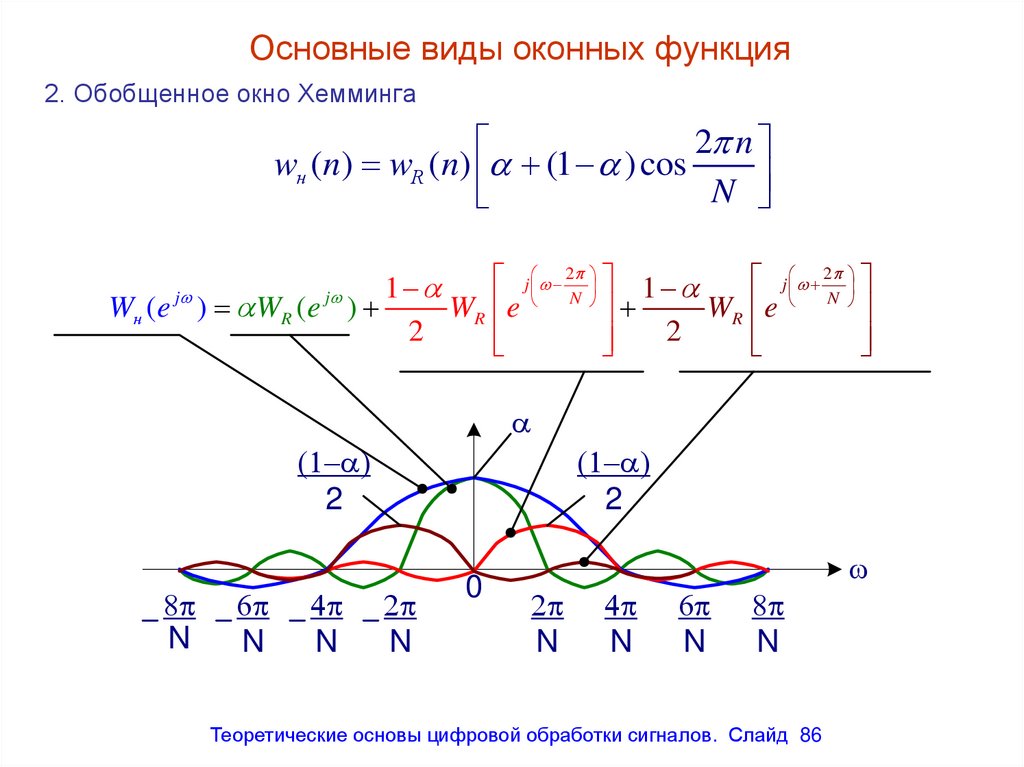

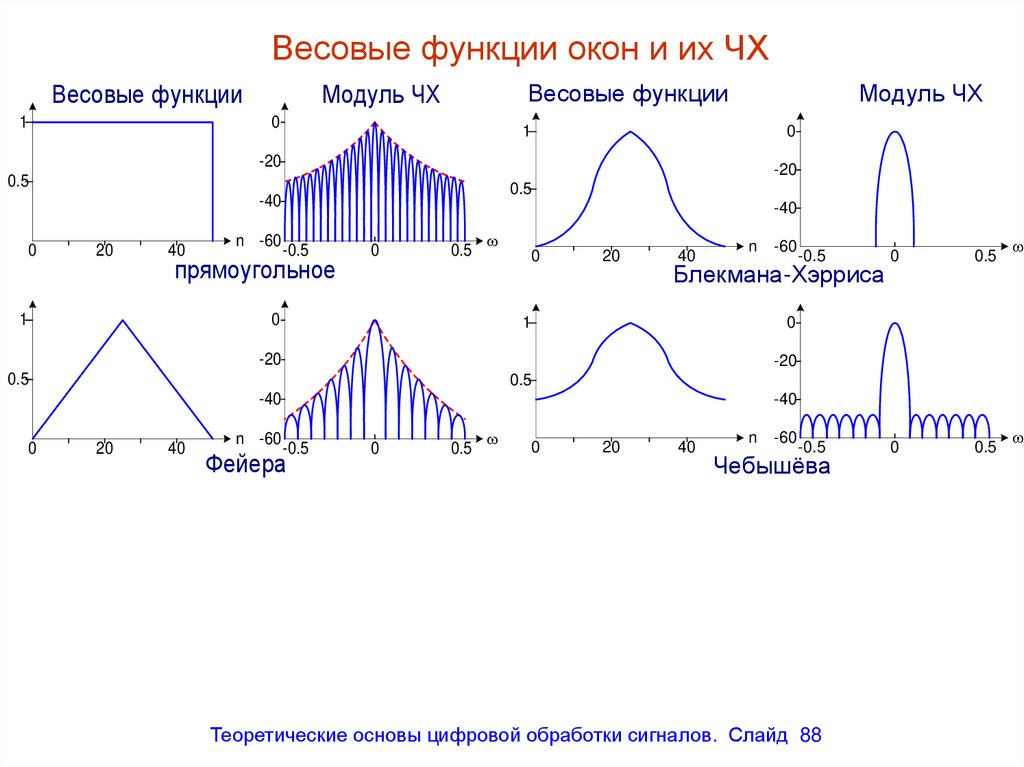


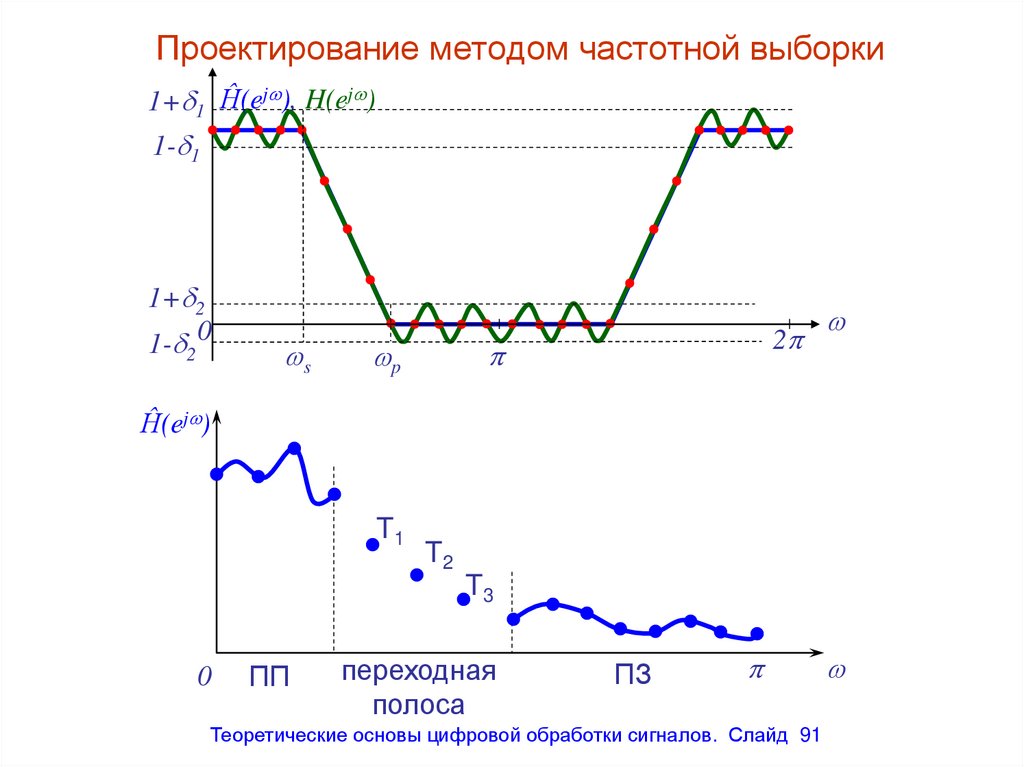


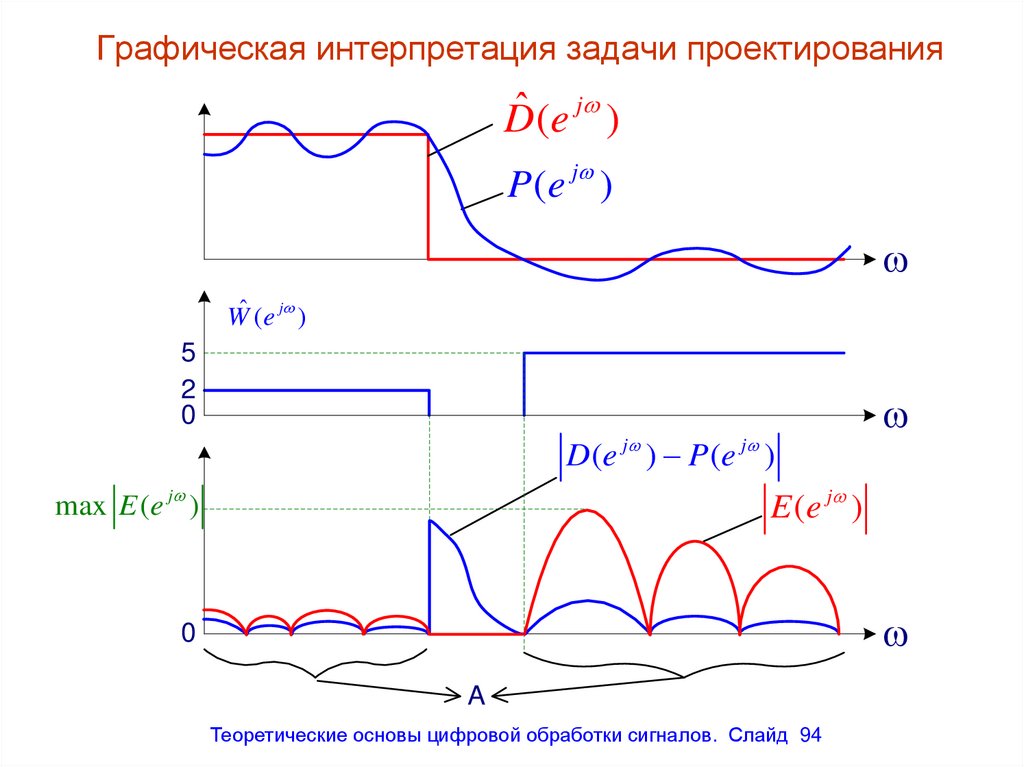
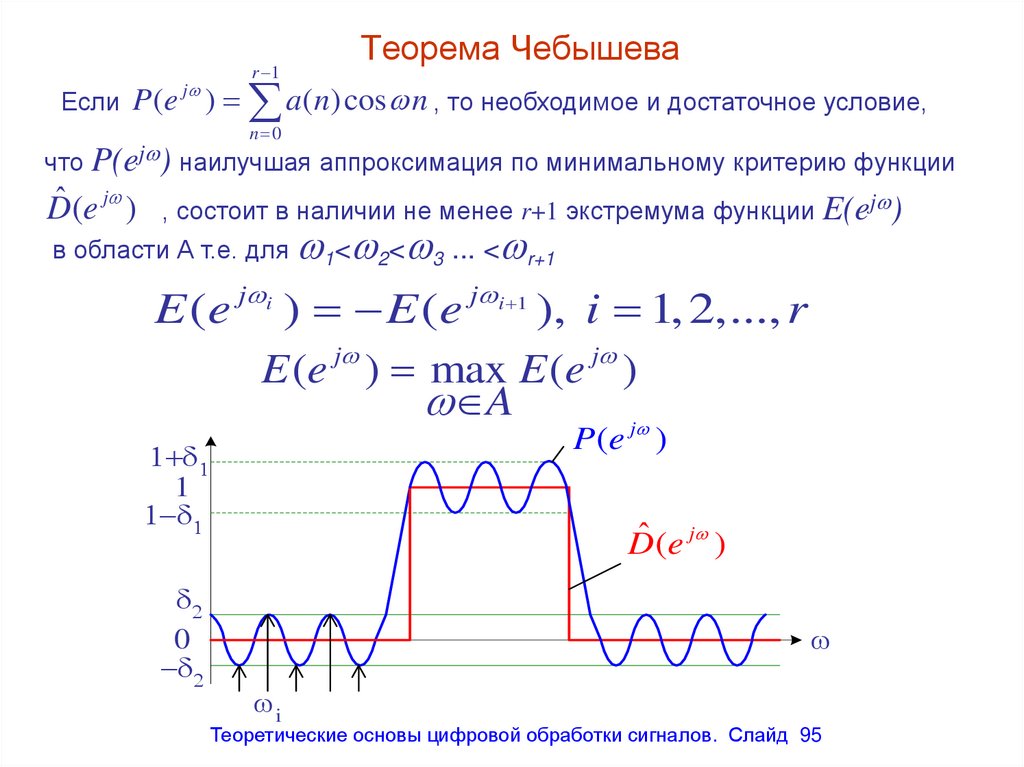

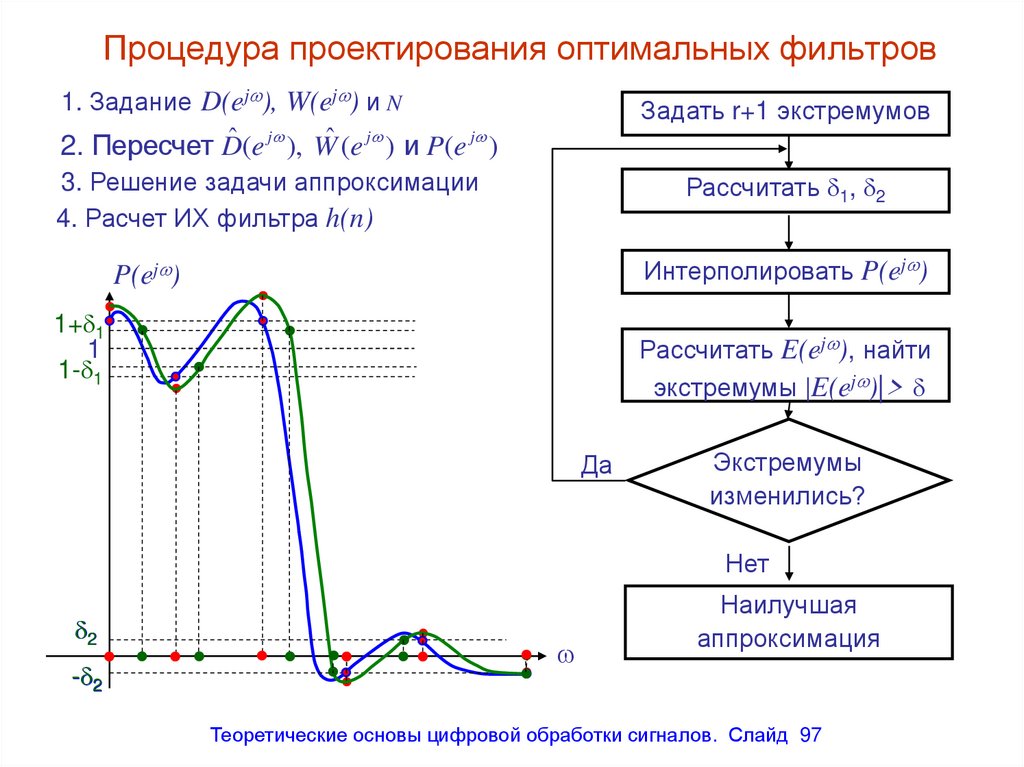
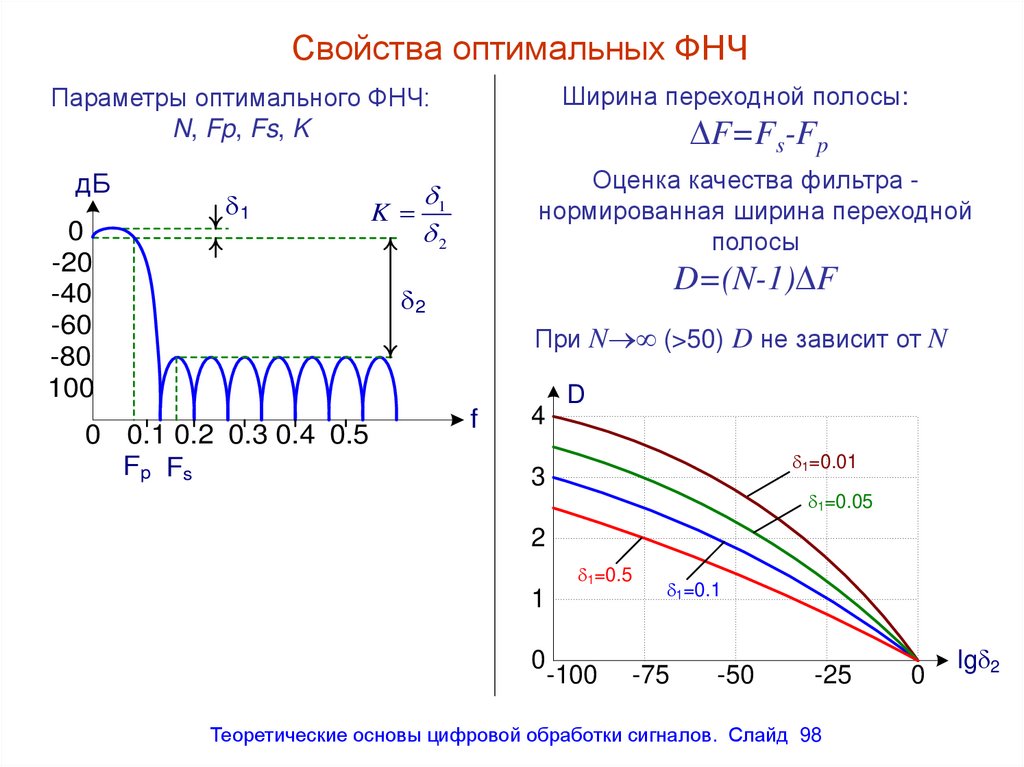
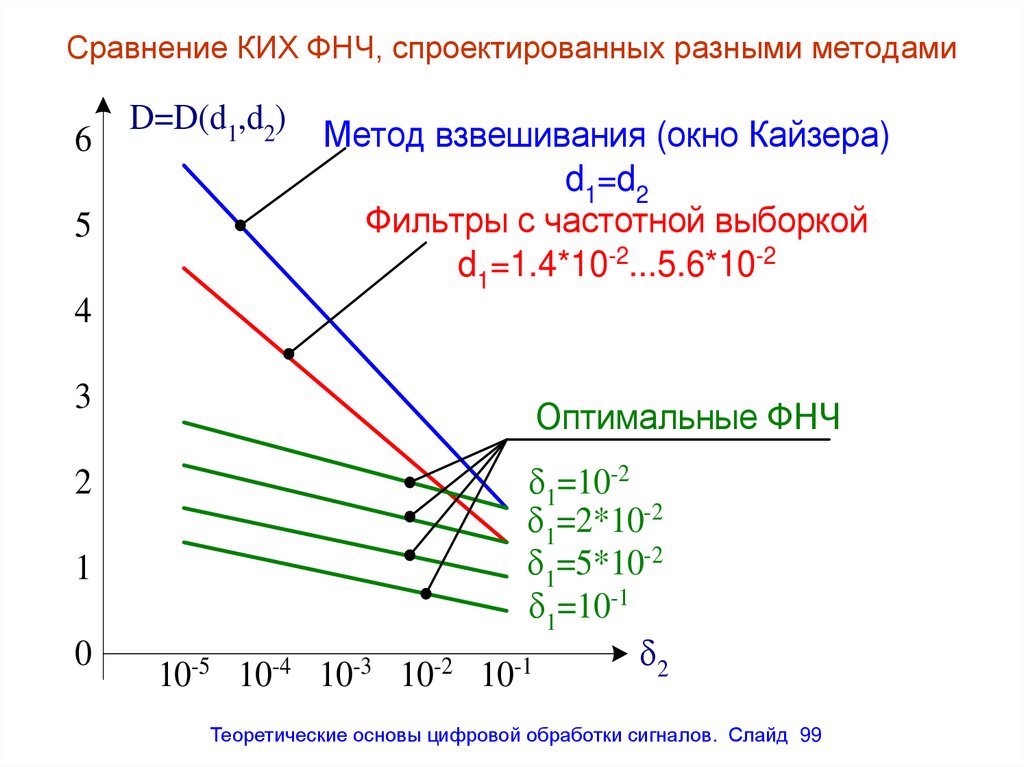

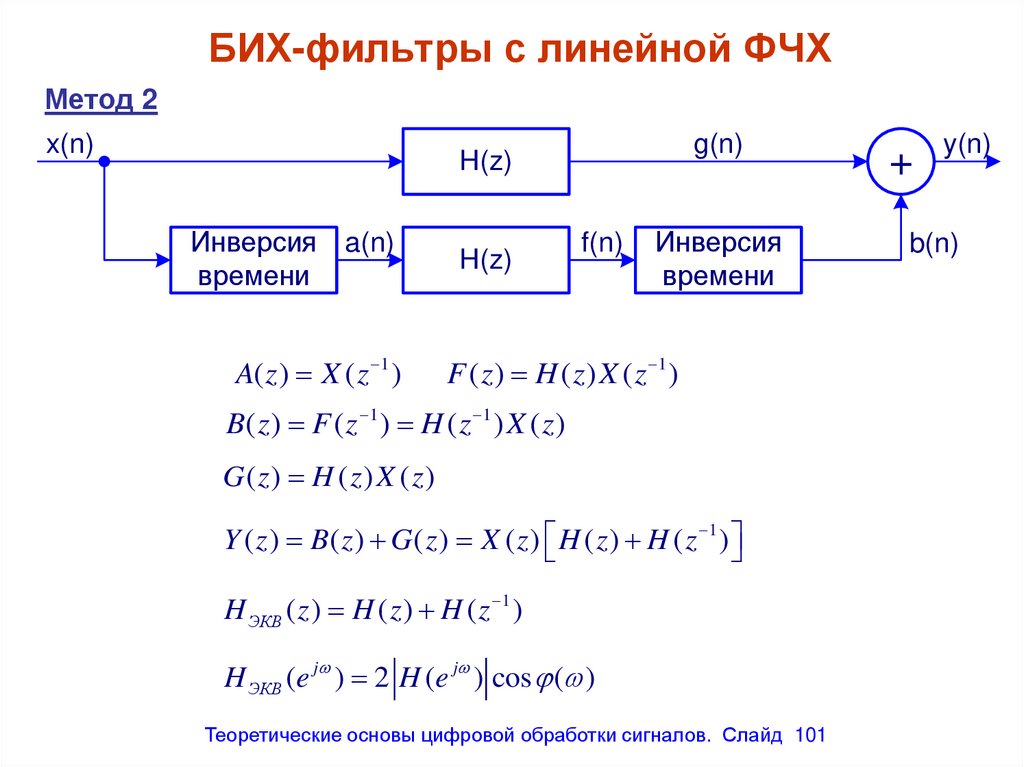
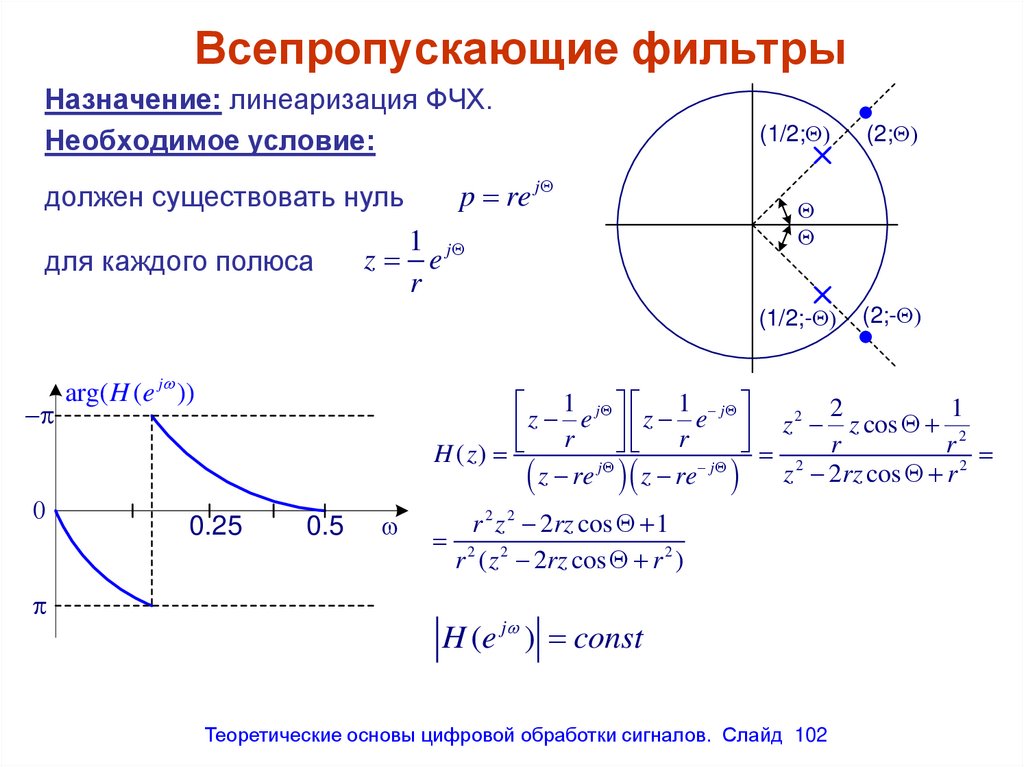


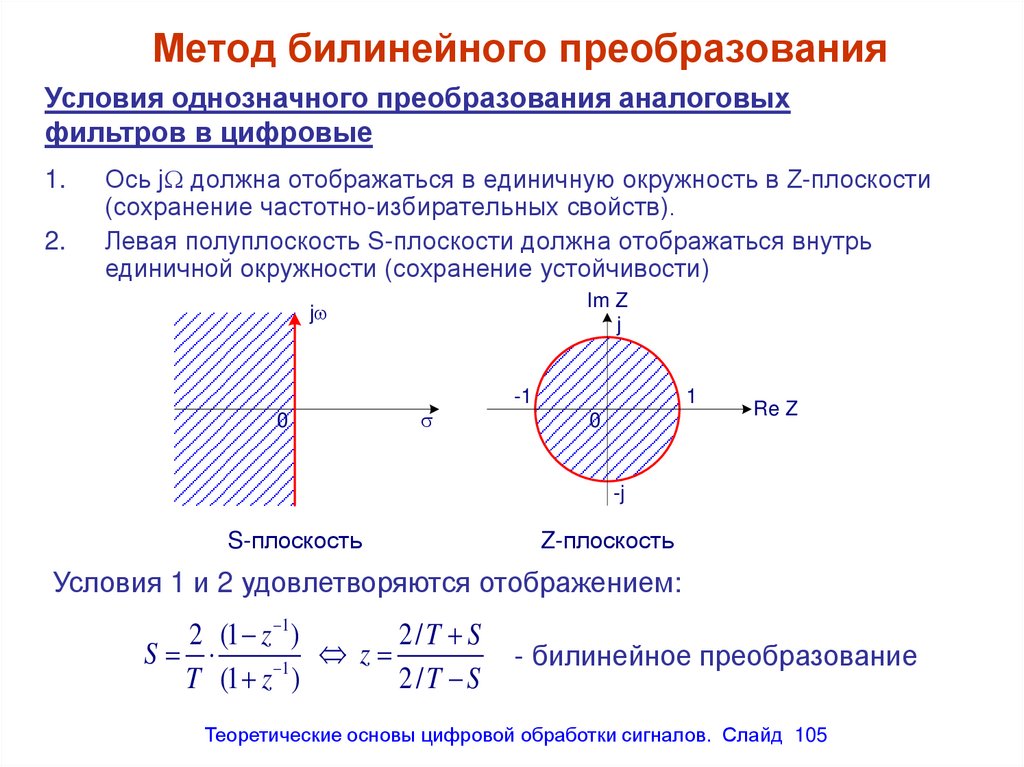

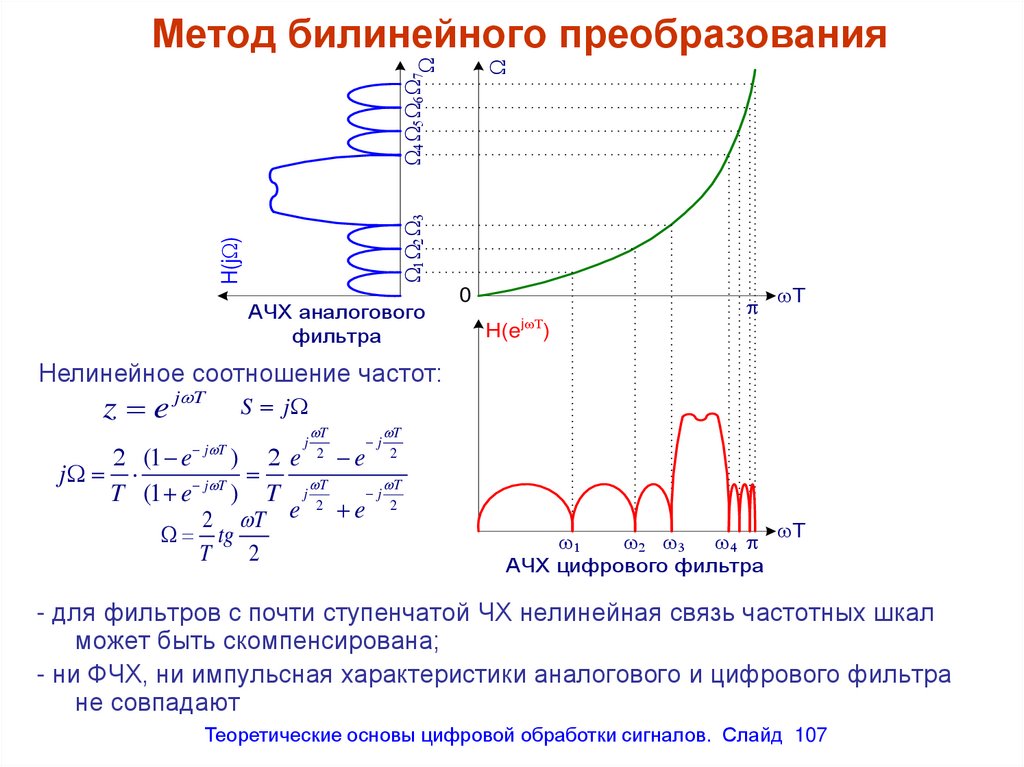
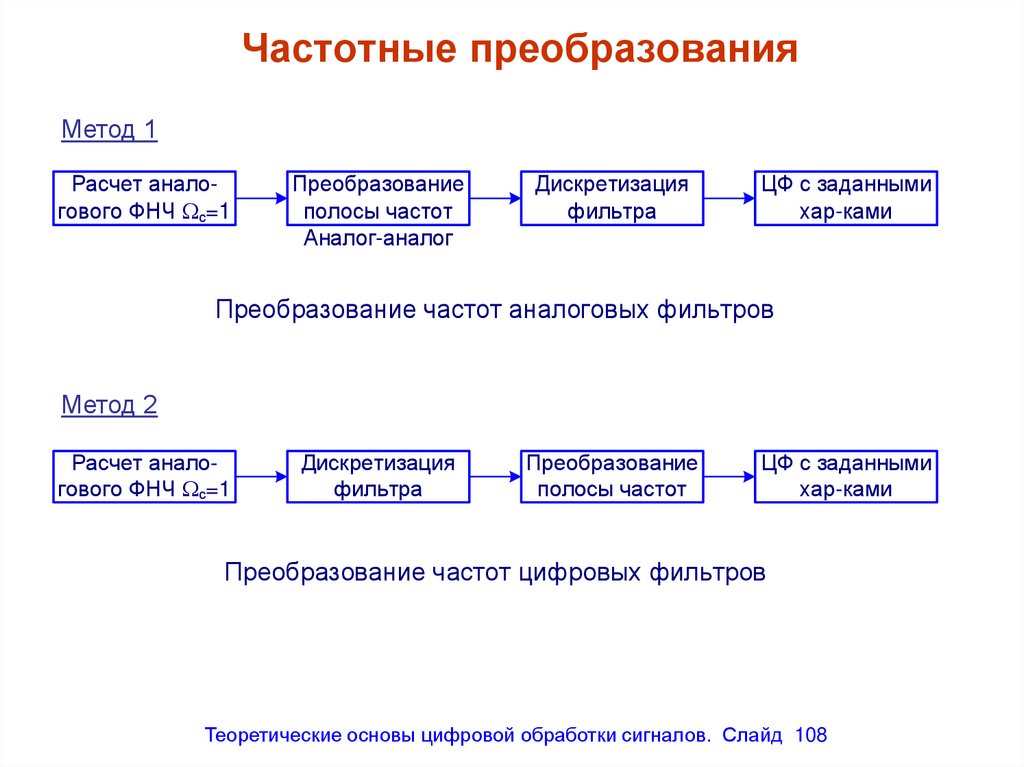


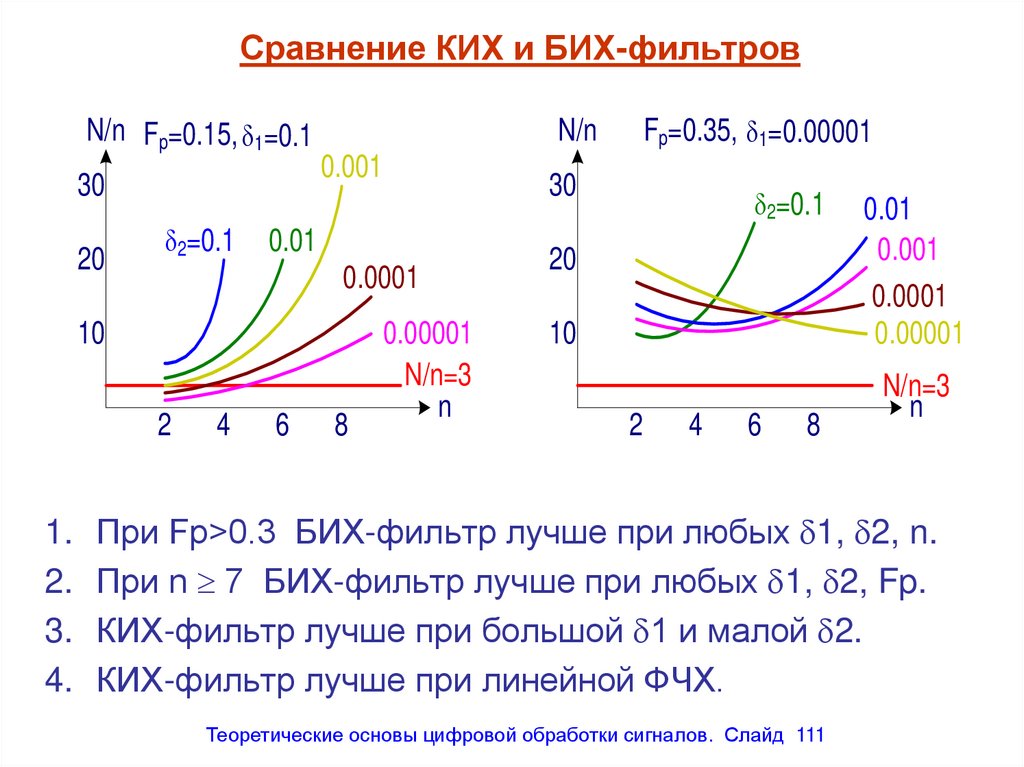

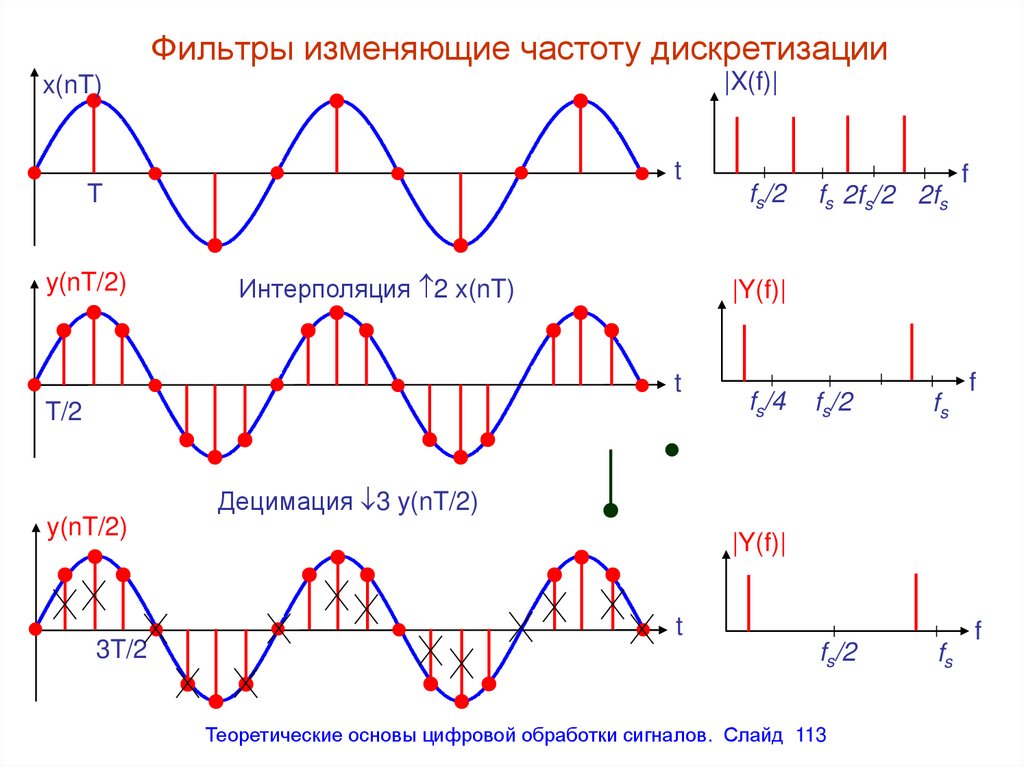
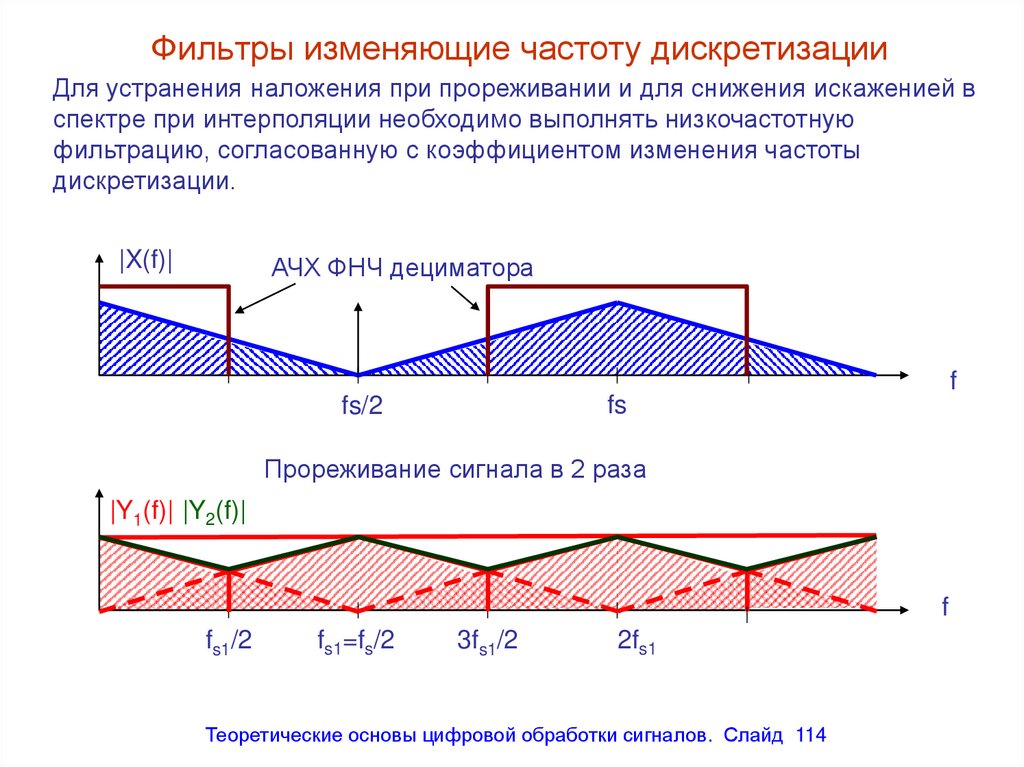
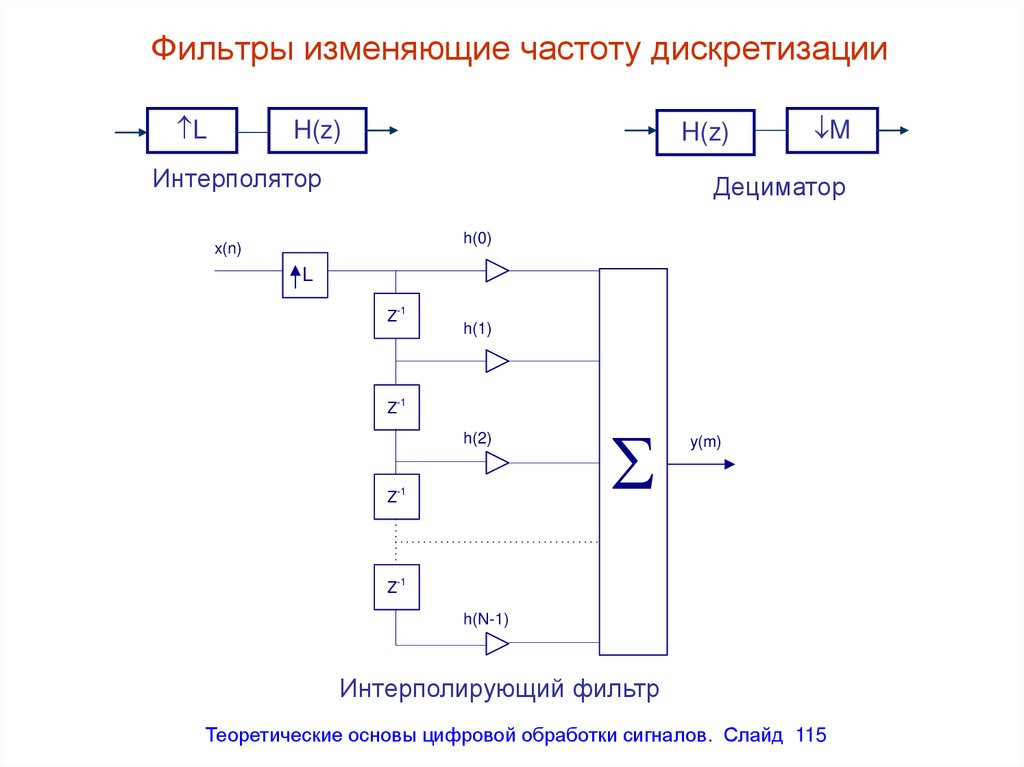
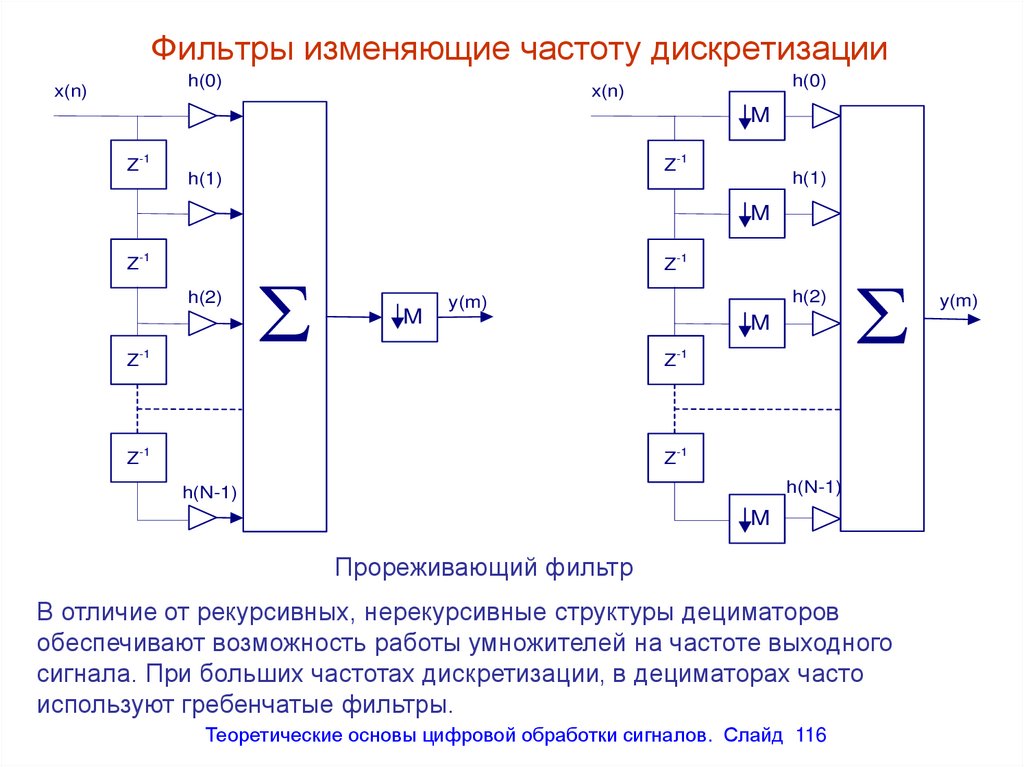

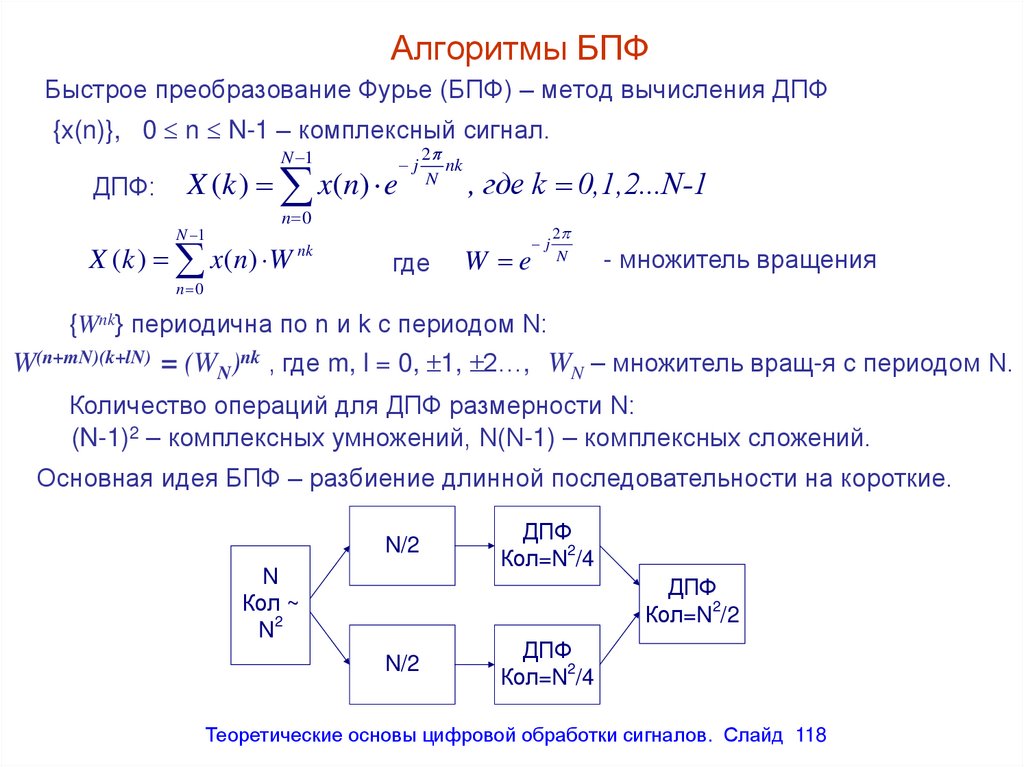


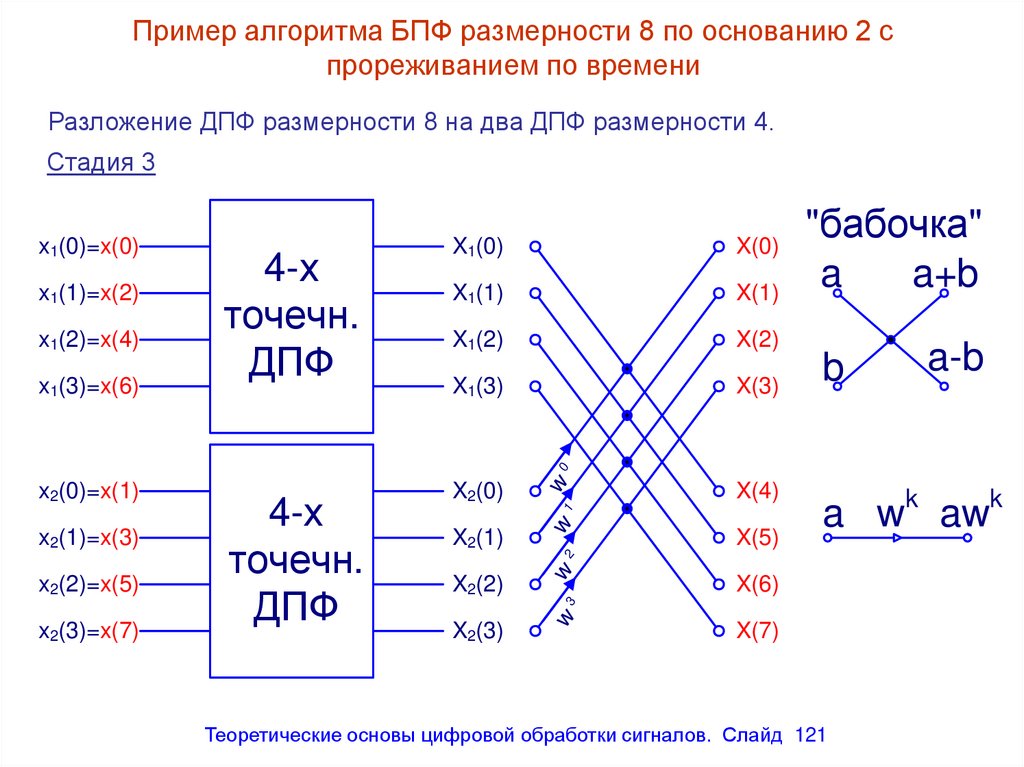
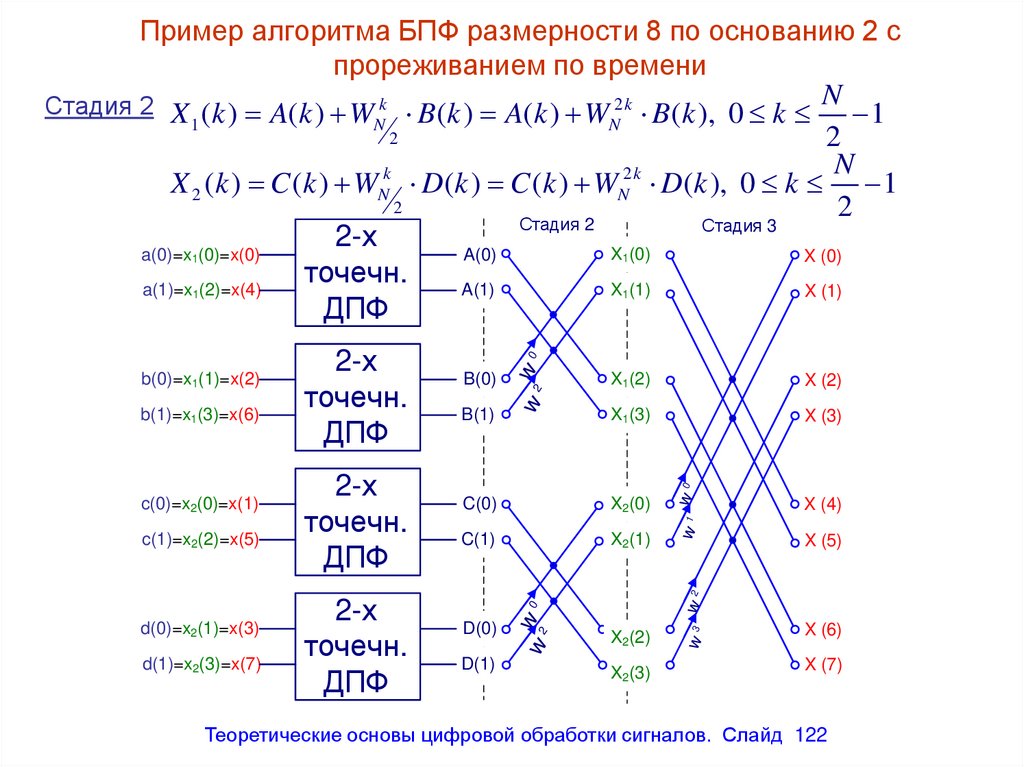
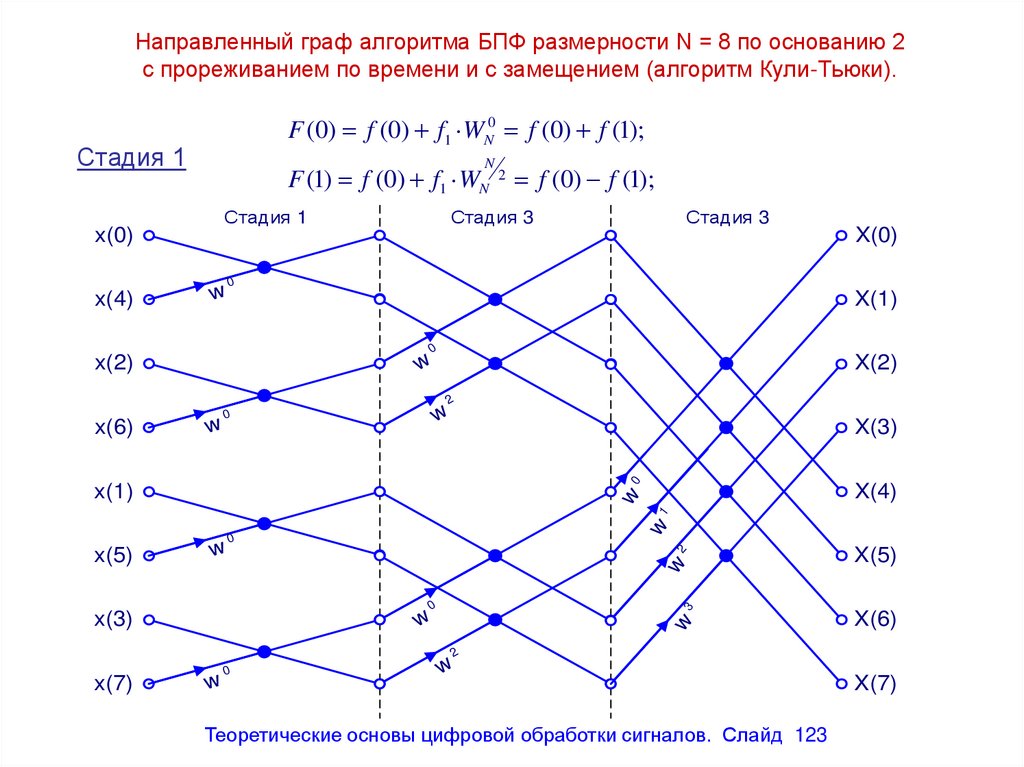

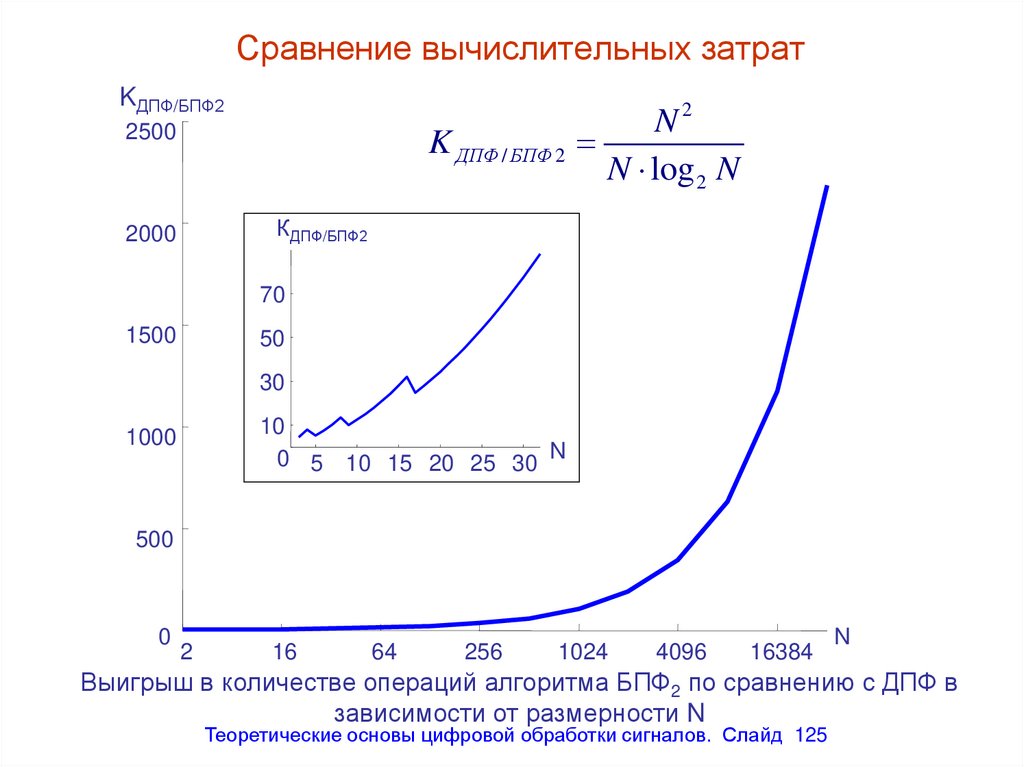
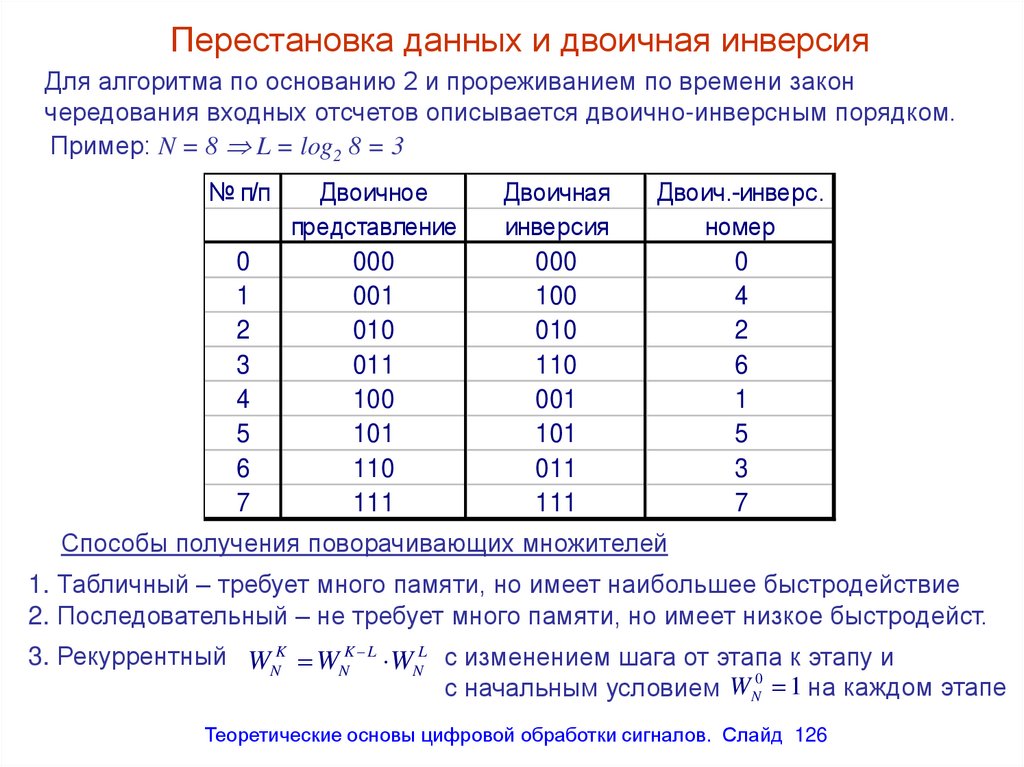


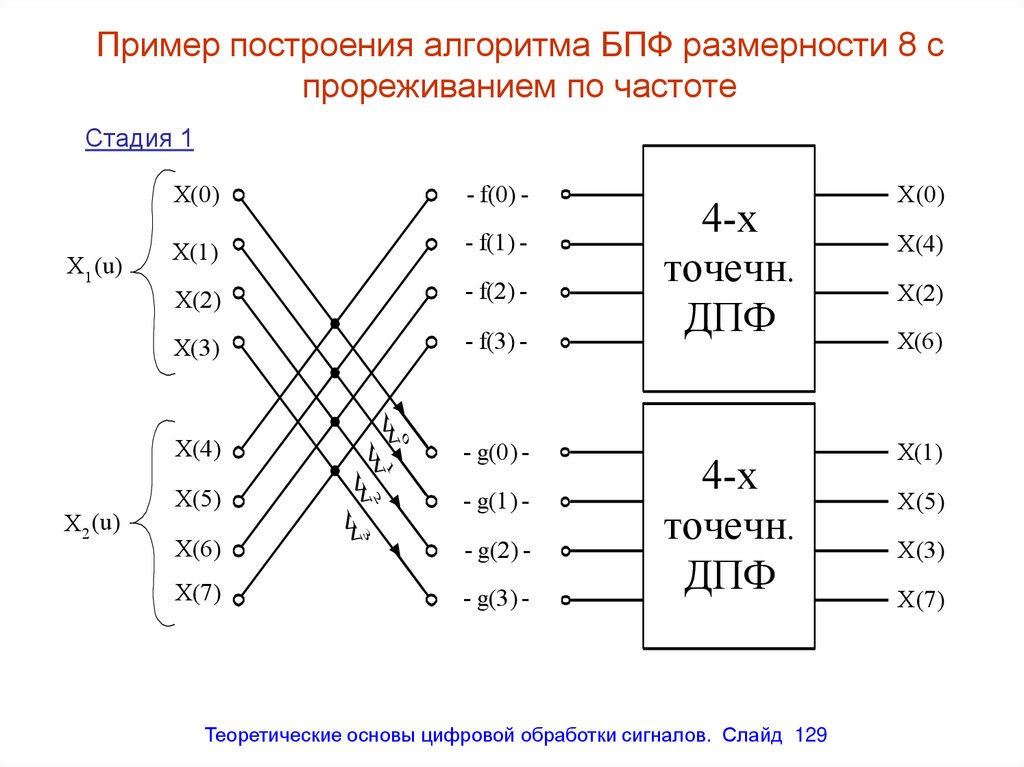



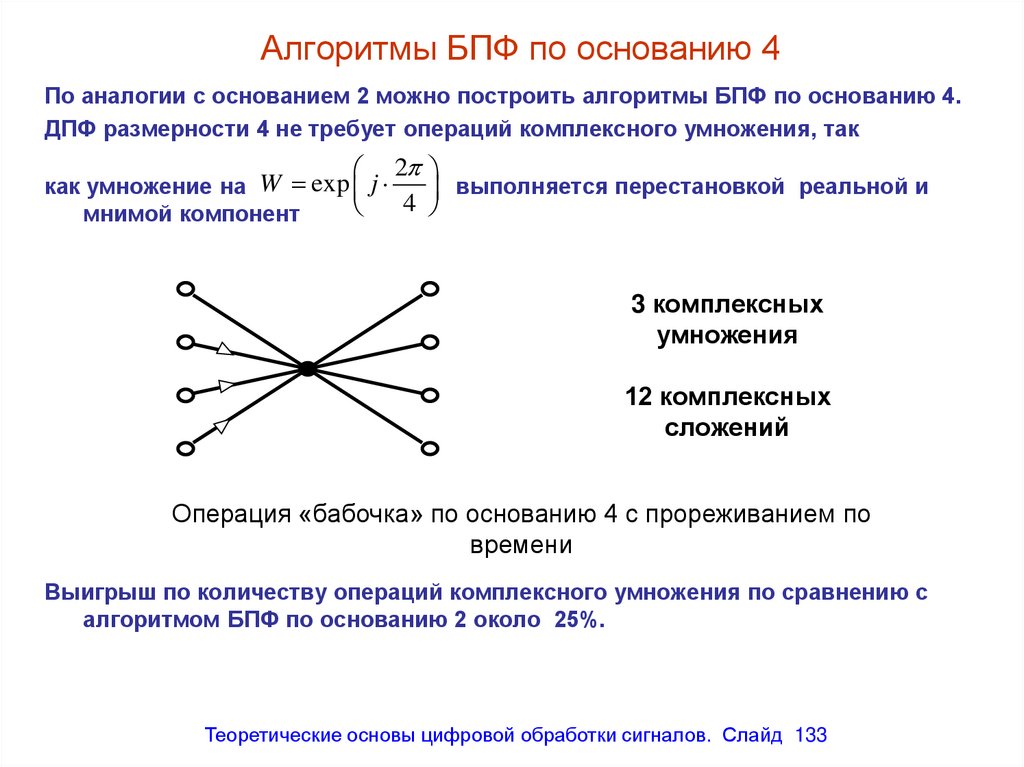


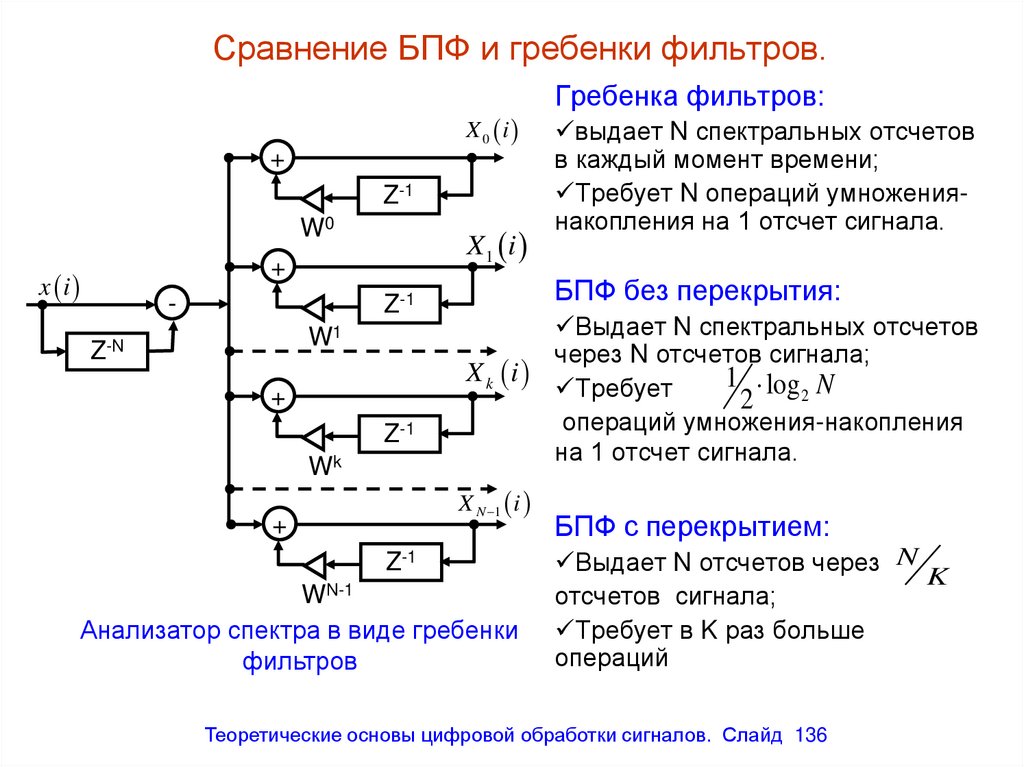
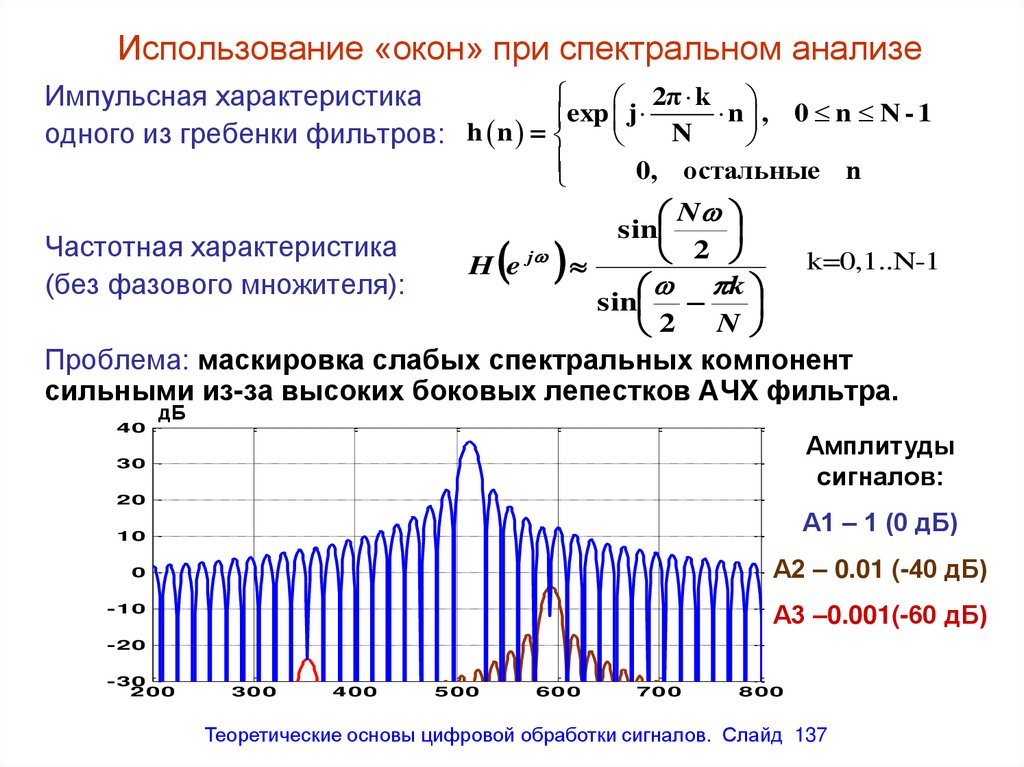
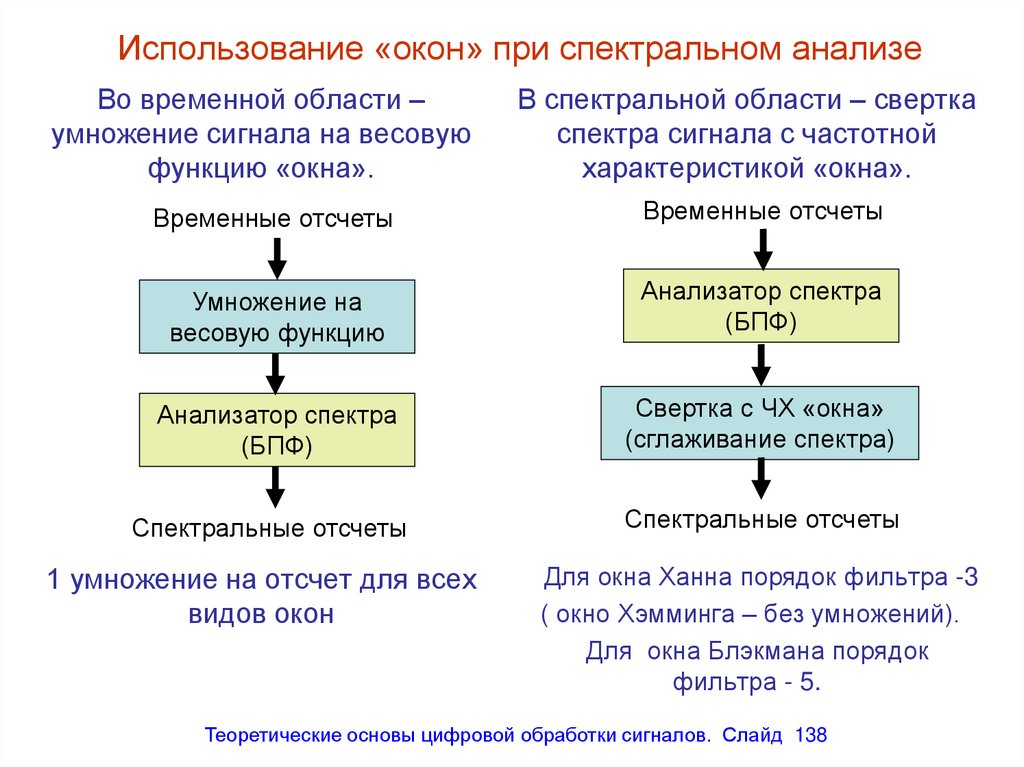
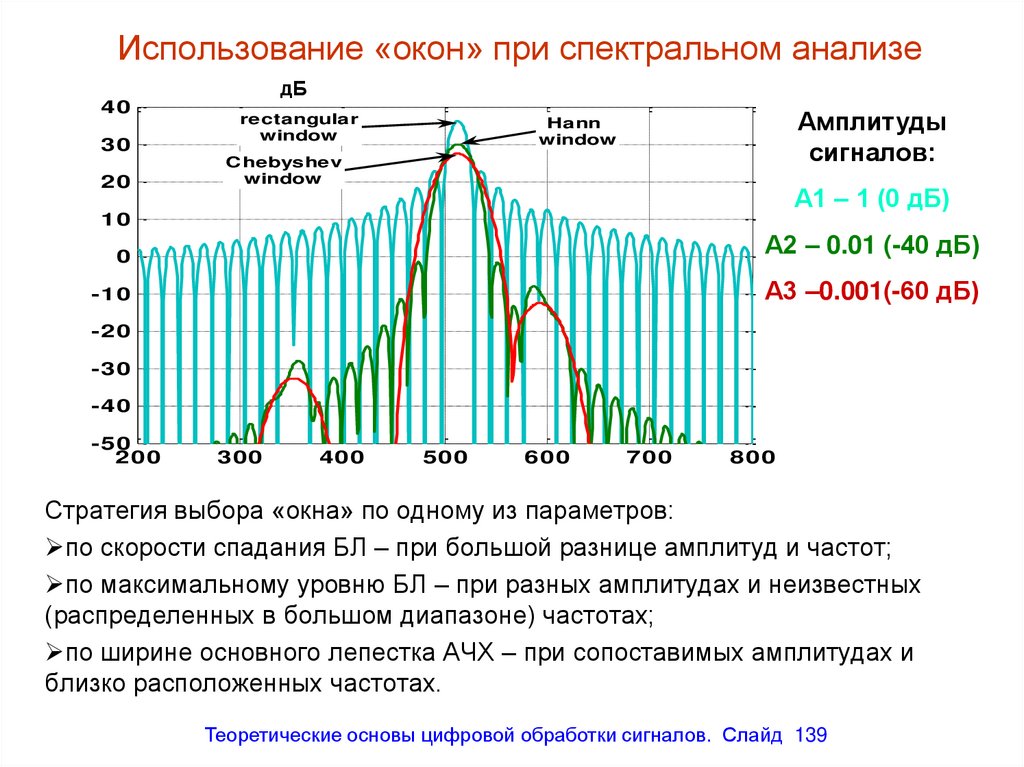




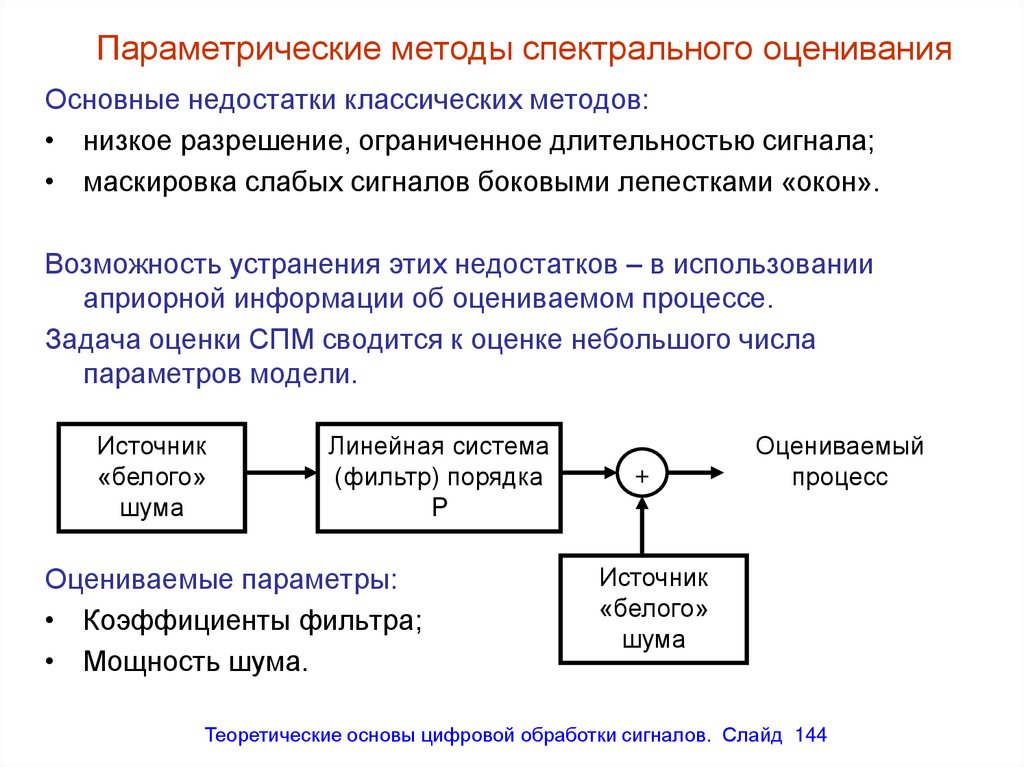
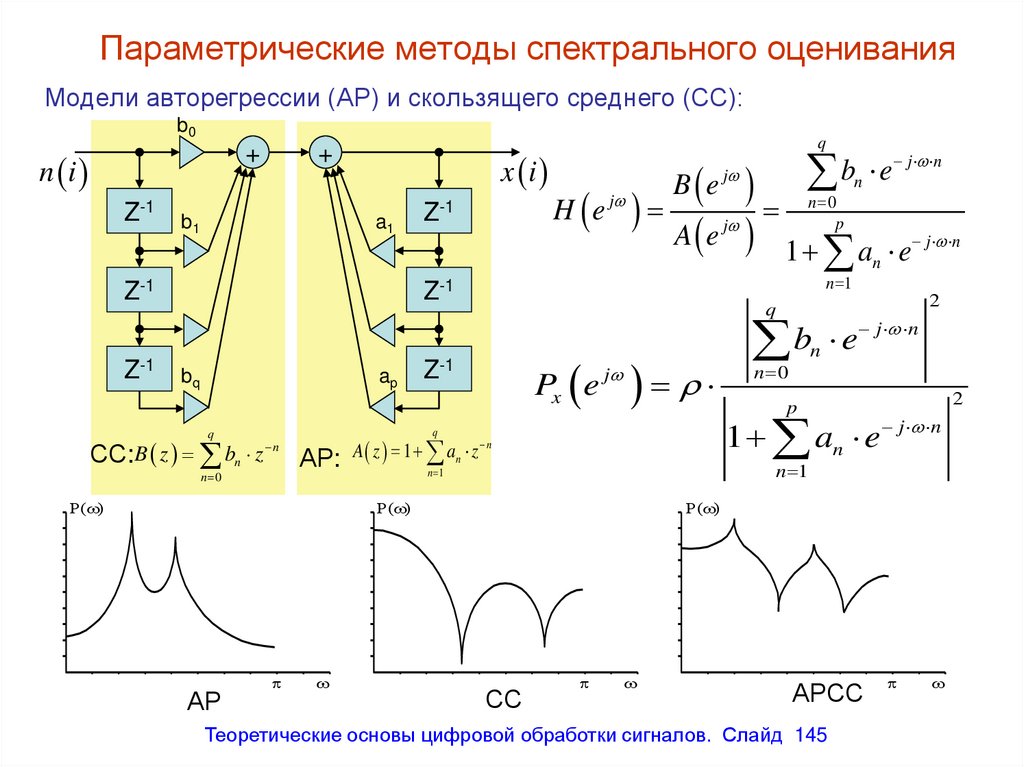


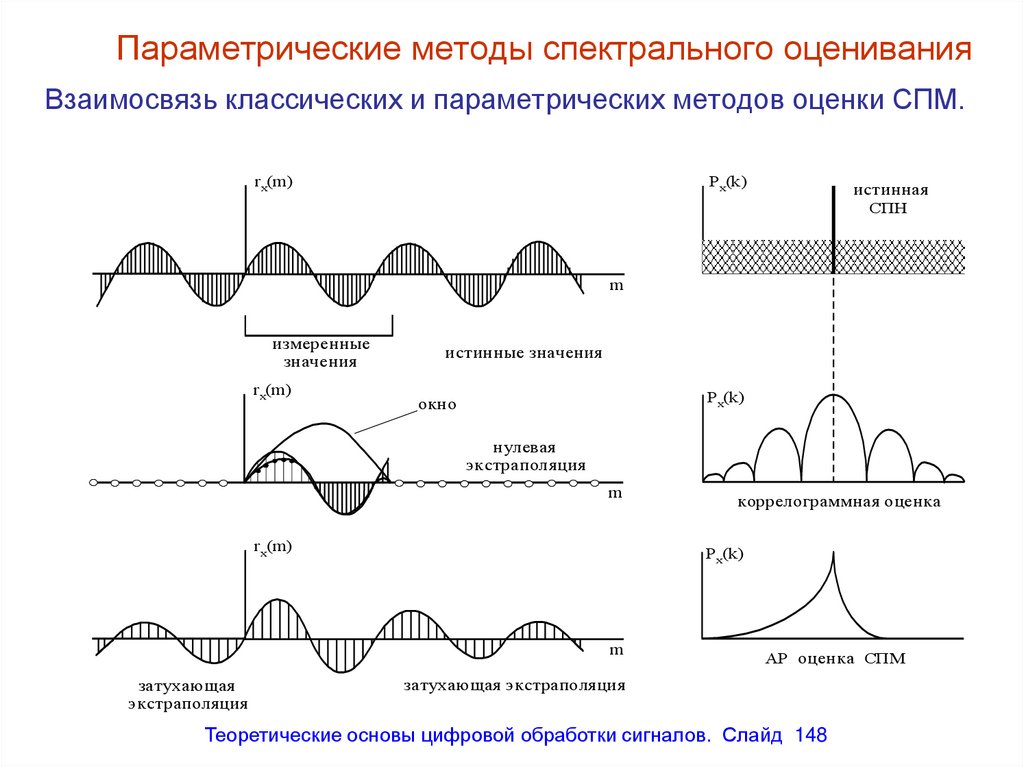
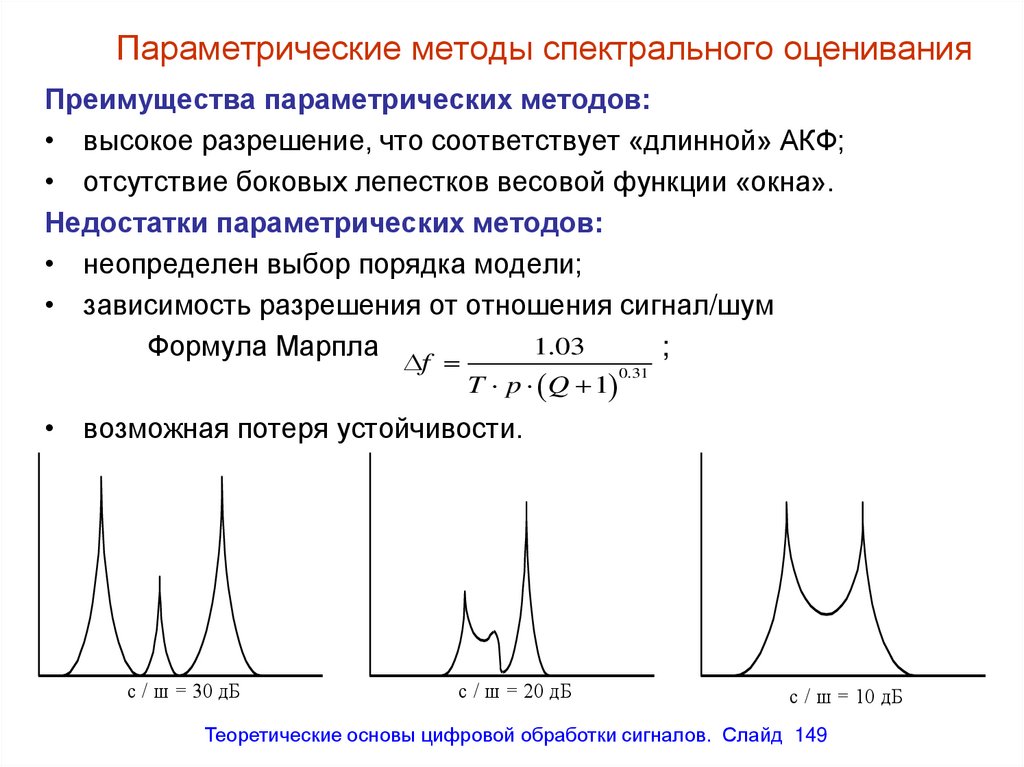
 Электроника
Электроника








