Случайные процессы. 7 семестр

1.

СЛУЧАЙНЫЕ ПРОЦЕССЫ
7 семестр

2.

СЛУЧАЙНЫЕ ПРОЦЕССЫ
Ранее были рассмотрены некоторые случайные во времени последовательности.
Теперь уделим внимание непрерывным во времени случайным величинам.
Если для каждого значения t зависимая переменная x представляет собой
случайную величину, то говорят, что х = x(t) есть случайная функция времени
или случайный процесс. Случайный процесс (случайная функция времени)
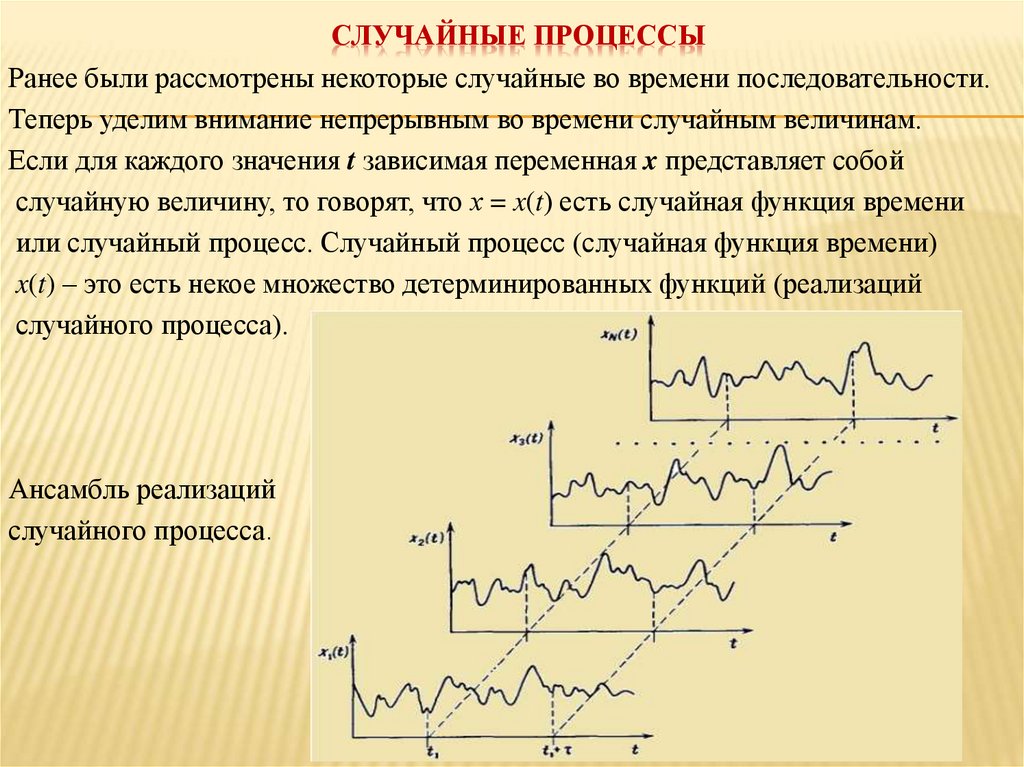
x(t) – это есть некое множество детерминированных функций (реализаций
случайного процесса).
Ансамбль реализаций
случайного процесса.

3.

СЛУЧАЙНЫЕ ПРОЦЕССЫ
Из определения случайного процесса в общем случае следует, что значение
случайного процесса в определенный момент времени t1 представляет собой
случайную величину. Из теории вероятности известно, что случайная величина
полностью задается интегральной функцией распределения или плотностью
вероятности Р(x). Однако для случайного процесса одномерная плотность
вероятности будет в общем случае зависеть от момента времени t (момент
времени, в который мы взяли «сечение» статистического ансамбля) как от
параметра Р(x, t).
Одномерная плотность вероятности Р(x, t).

4.

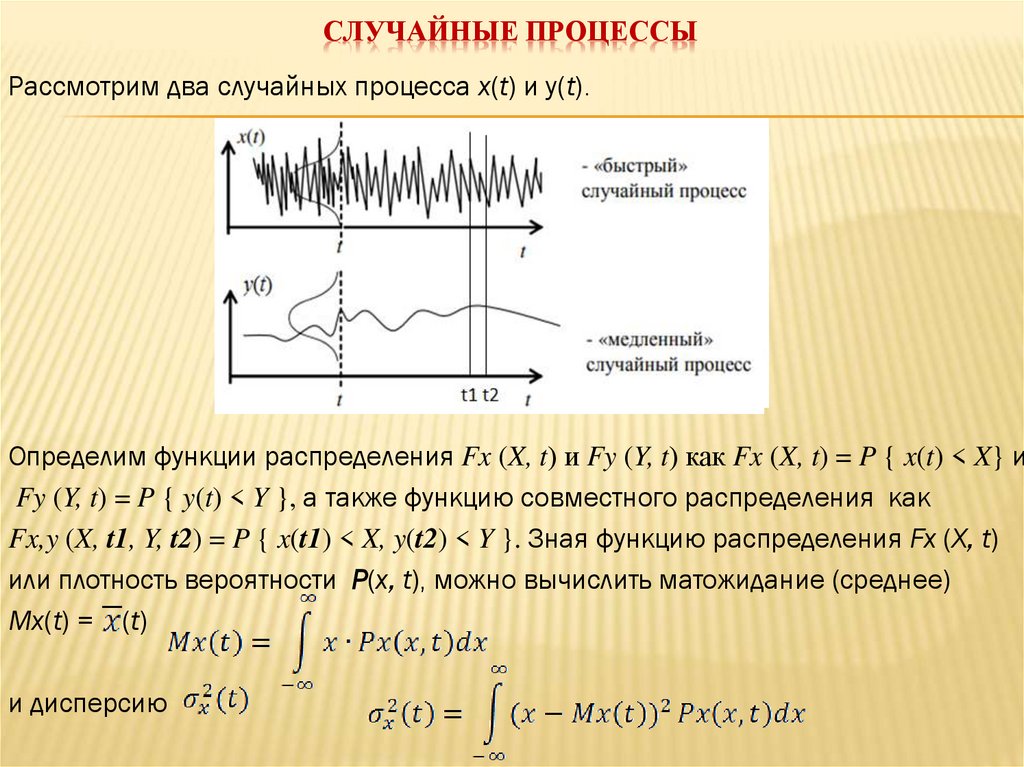
СЛУЧАЙНЫЕ ПРОЦЕССЫ
Рассмотрим два случайных процесса x(t) и y(t).
Определим функции распределения Fx (X, t) и Fy (Y, t) как Fx (X, t) = P { x(t) < X} и
Fy (Y, t) = P { y(t) < Y }, а также функцию совместного распределения как
Fx,y (X, t1, Y, t2) = P { x(t1) < X, y(t2) < Y }. Зная функцию распределения Fx (X, t)
или плотность вероятности Р(x, t), можно вычислить матожидание (среднее)
Mx(t) = (t)
и дисперсию

5.

СЛУЧАЙНЫЕ ПРОЦЕССЫ
как для случайного процесса x(t) так и для процесса y(t) My(t) = (t) и
. Для
рассмотренных процессов эти величины могут оказаться равными Mx(t) = My(t)
и
, однако эти процессы очевидно разные. Для близких значений
t1 и t2 величины x(t1) и x(t2) сильно отличаются, а величины y(t1) и y(t2)
практически неизменны. Для описания такой зависимости (связи) используется
корреляционная функция. В общем случае
или автокорреляционная функция процесса x(t)
В том случае, если Fx(X, t) = Fx(X) или Р(x, t) = Р(x) (распределения не зависят от
времени t), такие процессы называют стационарными. При этом Mx(t) = Mx = m
и
. Тогда

6.

СЛУЧАЙНЫЕ ПРОЦЕССЫ
Пусть t2 – t1 = τ, в этом случае
Заметим, что
и
.

7.

СЛУЧАЙНЫЕ ПРОЦЕССЫ
То есть для эргодического процесса
. Как правило, стационарный
процесс является эргодическим. Тогда корреляционную функцию можно
определить так
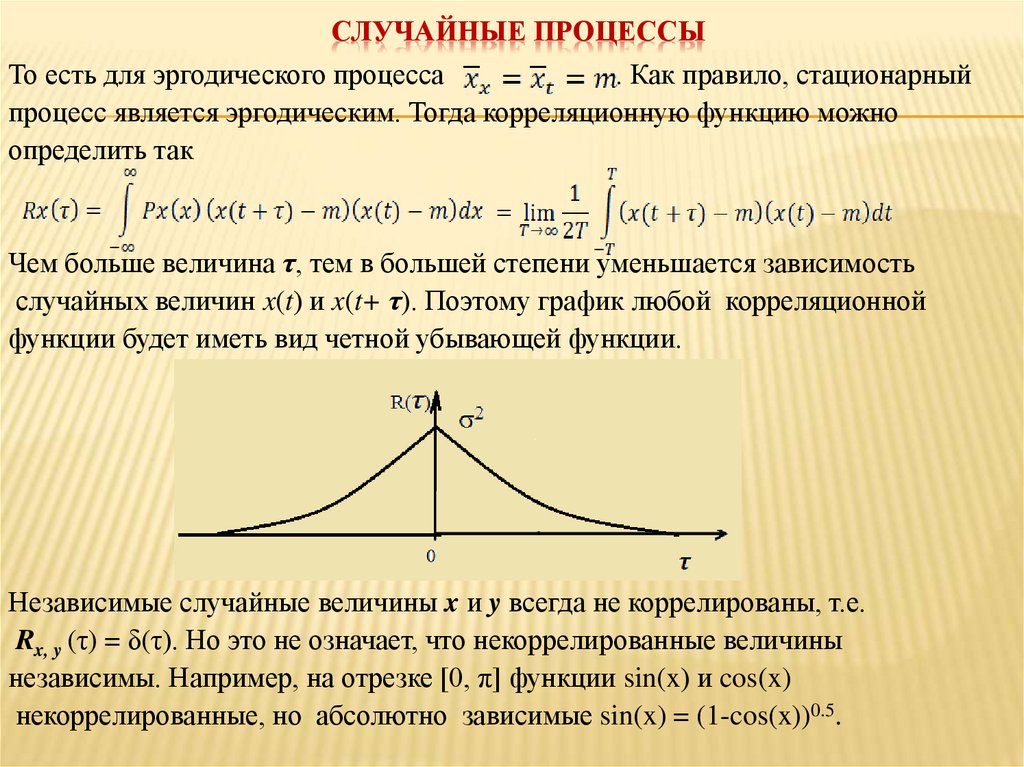
Чем больше величина τ, тем в большей степени уменьшается зависимость
случайных величин x(t) и x(t+ τ). Поэтому график любой корреляционной
функции будет иметь вид четной убывающей функции.
Независимые случайные величины x и y всегда не коррелированы, т.е.
Rx, y (τ) = δ(τ). Но это не означает, что некоррелированные величины
независимы. Например, на отрезке [0, π] функции sin(x) и cos(x)
некоррелированные, но абсолютно зависимые sin(x) = (1-cos(x))0.5.

8.

СЛУЧАЙНЫЕ ПРОЦЕССЫ
Часто на практике используется коэффициент корреляции r(τ) = R (τ)/
случайных величин x и y
или для
При этом -1 < r < 1 . Если r > 0, это означает что x и y ведут себя подобным
образом – одновременно убывают или возрастают. Если r < 0, это означает что x
и y изменяются в противоположных направлениях.
Обычно для удобства описания случайных процессов используется
центрированный случайный процесс
.
Если процесс x(t) имеет конечную энергию и квадратично интегрируем, то для
одной реализации процесса можно определить преобразование Фурье как
случайную комплексную функцию частоты:
Однако она оказывается почти бесполезной для описания ансамбля. Выходом
из этой ситуации является построение функции, характеризующей
распределение энергии процесса по оси частот.

9.

СЛУЧАЙНЫЕ ПРОЦЕССЫ
Тогда согласно теореме Парсеваля энергия
Функция
характеризует, таким образом, распределение энергии
реализации по оси частот и называется спектральной плотностью реализации.
Усреднив эту функцию по всем реализациям можно получить спектральную
плотность процесса. Рассмотрим Фурье-образ корреляционной функции R(τ)
центрированного процесса
t+τ=u
dt = du τ = u – t
Таким образом, Фурье-образ корреляционной функции R(τ) является
спектральной плотностью S(ω) (энергетическим спектром)

10.

СЛУЧАЙНЫЕ ПРОЦЕССЫ
Или
Очевидно, спектральная плотность
- четная функция и
В природе и технике «чисто» белый шум (то есть белый шум, имеющий
одинаковую спектральную мощность на всех частотах) не встречается (ввиду того,
что такой сигнал имел бы бесконечную мощность), однако под категорию белых
шумов попадают любые шумы, спектральная плотность которых одинакова (или
слабо отличается) в рассматриваемом диапазоне частот. Термин «белый шум»
обычно применяется к сигнал имеющему автокорреляционную функцию,
математически описываемую дельта-функцией Дирака по всем измерениям
многомерного пространства, в котором этот сигнал рассматривается. Сигналы,
обладающие этим свойством, могут рассматриваться как белый шум. Данное
статистическое свойство является основным для сигналов такого типа. То, что
белый шум не коррелирован по времени (или по другому аргументу), не
определяет его значений во временной (или любой другой рассматриваемой
аргументной) области.

11.

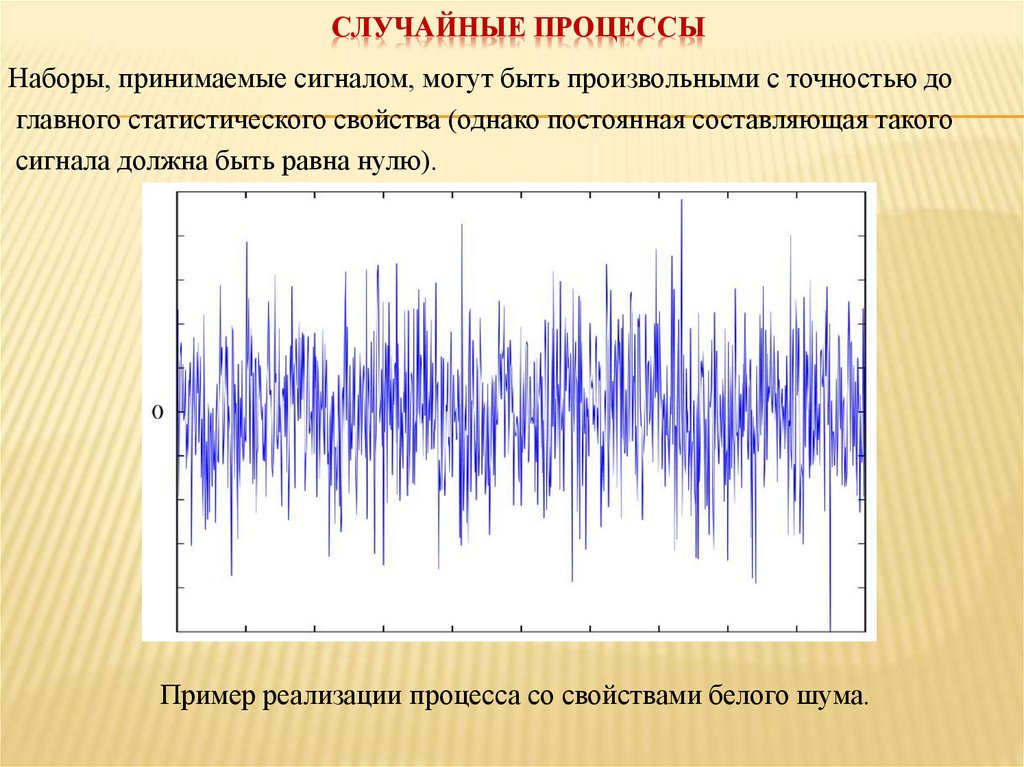
СЛУЧАЙНЫЕ ПРОЦЕССЫ
Наборы, принимаемые сигналом, могут быть произвольными с точностью до
главного статистического свойства (однако постоянная составляющая такого
сигнала должна быть равна нулю).
Пример реализации процесса со свойствами белого шума.

12.

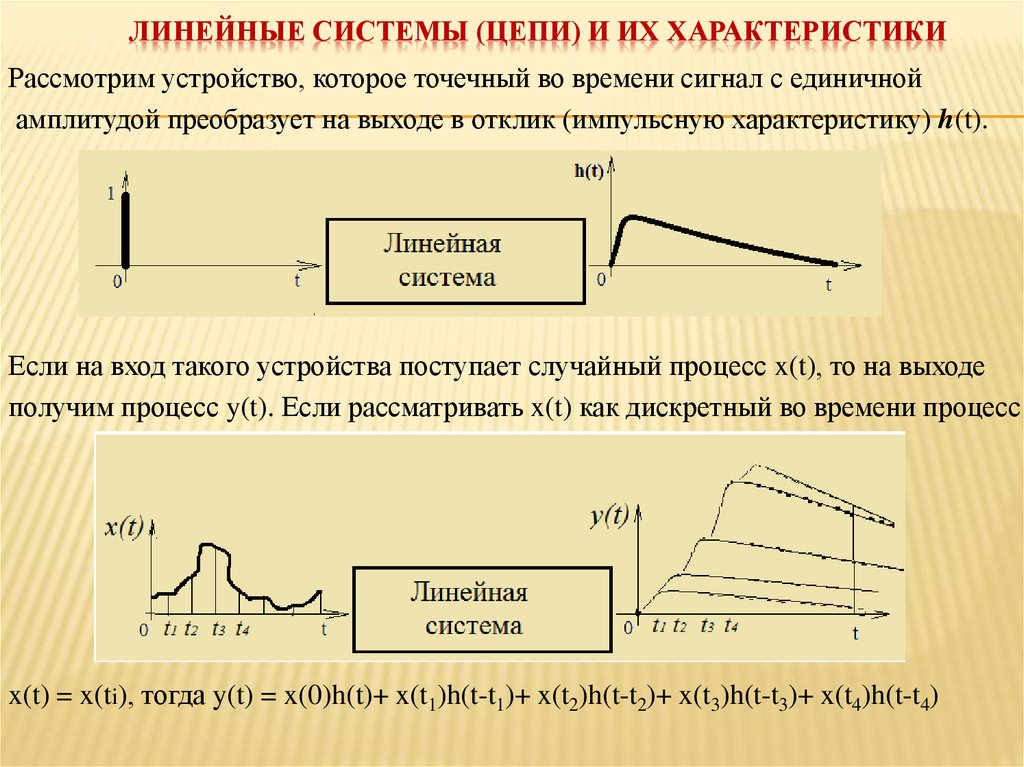
ЛИНЕЙНЫЕ СИСТЕМЫ (ЦЕПИ) И ИХ ХАРАКТЕРИСТИКИ
Рассмотрим устройство, которое точечный во времени сигнал с единичной
амплитудой преобразует на выходе в отклик (импульсную характеристику) h(t).
Если на вход такого устройства поступает случайный процесс x(t), то на выходе
получим процесс y(t). Если рассматривать x(t) как дискретный во времени процесс
x(t) = x(ti), тогда y(t) = x(0)h(t)+ x(t1)h(t-t1)+ x(t2)h(t-t2)+ x(t3)h(t-t3)+ x(t4)h(t-t4)

13.

ЛИНЕЙНЫЕ СИСТЕМЫ (ЦЕПИ) И ИХ ХАРАКТЕРИСТИКИ
Или для непрерывного процесса
Пусть оригиналам соответствуют Фурье-образы x(t) X(ω), y(t) Y(ω), h(t) H(ω).
тогда по теореме о свертке Y(ω) = H(ω)X(ω). Функция H(ω) = Y(ω)/X(ω)
называется передаточной функцией системы. Для спектральной плотности y(t)
будет справедливо выражение
. Если процесс x(t)
проходит через n линейных систем, тогда на выходе получим
Y(ω) =H1(ω)H2(ω)H3(ω)…Hn(ω)X(ω) и
Рассмотрим простейшие линейные цепи – дифференцирующую и интегрирующую.

14.

ЛИНЕЙНЫЕ СИСТЕМЫ (ЦЕПИ) И ИХ ХАРАКТЕРИСТИКИ
Для дифференцирующей цепи
Для интегрирующей цепи
и
и
Как изменится спектральная плотность белого шума при прохождении через
1. Дифференцирующую цепь?
2. Интегрирующую цепь?
3. Последовательно соединенные обе цепи?