Похожие презентации:
Свойства и способы вычисления двойных интегралов. Двойной интеграл в прямоугольных декартовых и полярных координатах. Лекция 15
1. Лекция 15
Двойные интегралы. Свойства двойныхинтегралов. Способы вычисления
двойных интегралов. Двойной интеграл
в прямоугольных декартовых и
полярных координатах.
2.
1. Объем цилиндрического тела. Двойной интеграл.Рассмотрим задачу об определении объема цилиндрического тела
Определение
Цилиндрическим телом называется тело, ограниченное замкнутой областью
D плоскости ОХУ, поверхностью z=f(x,y), где функция f(x,y) непрерывна и
неотрицательна в области D и цилиндрической поверхностью с
образующей параллельной оси OZ и направляющей – границей области D.
Область D –основание цилиндрического
тела. Граница области состоит из одной
или нескольких замкнутых
кусочно-гладких линий.
В частных случаях боковая цилиндрическая
поверхность может отсутствовать.
Например, тело, ограниченное
плоскостью ОХУ и верхней полусферой:
z
R2 x2 y2
3.
Объем тела можно представить как сумму или разность объемовцилиндрических тел. Принципы, лежащие в основе определения объема тела
следующие:
1. Если разбить тело на части, то его объем будет равен сумме объемов всех
частей;
2. Объем прямого цилиндра, то есть цилиндрического тела, ограниченного
плоскостью параллельной плоскости ОХУ, равен площади основания
умноженной на высоту тела.
Обозначения:
V - искомый объем цилиндрического тела;
1 , 2 ,..., n - частичные области, получаемые при разбиении области D
на n замкнутых областей произвольной формы;
1 , 2 ,..., n - площади частичных областей
Через границу каждой области проведем цилиндрическую поверхность с
образующей параллельной OZ. Эти цилиндрические поверхности разрежут
поверхность z=f(x,y) на n кусков, соответствующих n частичным областям.
Цилиндрическое тело разбивается на n частичных цилиндрических тел.
4.
iВыберем в каждой частичной области i произвольную точку Pi ( xi , yi )
и заменим соответствующее частичное цилиндрическое тело прямым
цилиндром с тем же основанием и высотой равной z i f ( xi , yi ). В результате
получим n – ступенчатое тело, объем которого равен
n
Vn f ( x1 , y1 ) 1 ... f ( x n , y n ) n f ( xi , y i ) i
i 1
z i f ( xi , y i )
i
Принимая V данного цилиндрического тела, приближенно равным объему
построенного n – ступенчатого тела, будем считать, что V n точнее выражает V,
чем больше n меньше каждая из частичных областей.
5.
Переходя к пределу при n , будем требовать, чтобы не только площадькаждой частичной области стремилась к 0, но чтобы стремились к 0 все ее
размеры. Если назвать диаметром замкнутой ограниченной области
наибольшее расстояние между точками ее границы, то высказанное
требование означает, что диаметры частичных областей стремятся к 0, а
области стягиваются в точку.
n
Таким образом V lim Vn lim n f ( x1 , y1 ) 1 ... f ( xn , yn ) n lim n f ( xi , yi ) i
i 1
(при стремлении к 0 наибольшего размера частичных областей при ).
К отысканию подобных сумм для функции двух переменных приводят и
другие задачи.
Рассмотрим вопрос в общем случае
Пусть
f(x,y)–функция, ограниченная в некоторой замкнутой ограниченной области D.
i - частичная область области D.
i - площадь частичной области .
Pi ( xi , yi ) i , f ( xi , yi ) значение функции в точке Pi ( xi , yi ) .
n
Составим сумму f ( xi , y i ) i (*)
i 1
6.
Сумма (*) называется интегральной суммой для функции f(x,y) в области D,соответствующей данному разбиению области D на n – частичных областей.
Определение
Двойным интегралом от функции f(x,y) по области D называется предел, к
которому стремится интегральная сумма при стремлении к 0 наибольшего
диаметра частичных областей
Запись n
lim n f ( xi , yi ) i f ( x, y)d
i 1
D
«Двойной интеграл от функции f(x,y) по области D»
f ( x, y)d - подынтегральное выражение;
f(x,y) – подынтегральная функция;
d - элемент площади;
D – область интегрирования.
Таким образом, объем цилиндрического тела, рассмотренного выше
выражается двойным интегралом от функции f(x,y), взятым по области,
являющейся основанием цилиндрического тела V f ( x, y)d
D
7.
Теорема существования двойного интегралаЕсли f(x,y) непрерывна в замкнутой ограниченной области D, то ее
интегральная сумма стремится к пределу при стремлении к 0 наибольшего
диаметра частичных областей. Этот предел, то есть f ( x, y)d не зависит от
D
способа разбиения области на частичные области i и выбора в них точек
Pi ( xi , yi ) .
Свойства двойных интегралов
Замечание
Свойства двойного интеграла почти такие же как соответствующие свойства
определенного интеграла.
1. Двойной интеграл от суммы конечного числа функций равен сумме
интегралов от слагаемых функций: f1 ( x, y) ... f n ( x, y) d f1 ( x, y)d ... f n ( x, y)d
D
D
D
2. Постоянный множитель подынтегральной функции можно выносить за
символ двойного интеграла: сf ( x, y)d с f ( x, y)d
D
D
3. Если область D разбита на две области без общих внутренних точек, то:
f ( x, y)d f ( x, y)d f ( x, y)d
D
D1
D2
8.
4. Если во всех точках области D функция f ( x, y) ( x, y )то: f ( x, y)d ( x, y)d
D
D
Следствие
Если подынтегральная функция в области интегрирования не меняет своего
знака, то двойной интеграл от функции того же знака, что и функция.
Свойство 3 и следствие свойства 4 позволяют уточнить геометрический смысл
двойного интеграла
Если объему цилиндрического тела, расположенному над плоскостью ОХУ
приписываем знак «+», а расположенного под плоскостью ОХУ – знак «-»,
если z=f(x,y) – уравнение ограничивающей поверхности, тогда f ( x, y)d
D
- алгебраическая сумма объемов тел, соответствующих положительным
и
отрицательным значениям функции f(x,y).
Если f(x,y)=1, то d S , где S – площадь области интегрирования.
D
Двойной интеграл выражает объем прямого цилиндра с высотой равной 1, то
есть объем численно равен площади основания.
9.
5. Значение двойного интеграла заключено между произведенияминаименьшего (m) и наибольшего (M) значений подынтегральной функции в
области D на площадь области интегрирования: mS f ( x, y)d MS , где S D
площадь области D.
6. Двойной интеграл равен произведению значения подынтегральной
функции в некоторой точке области интегрирования на площадь области
интегрирования, то есть: f ( x, y)d f ( , )S , f ( , ) - среднее значение
D
функции f(x,y) в области D.
Вычисление двойных интегралов
При вычислении f ( x, y)d элемент d удобнее представлять в следующем
D
виде.
Область D в плоскости ОХУ разбивается на частичные области посредством
двух систем координатных линий: x=const, y=const. Эти прямые
соответственно параллельны ОХ и ОУ. Частичные области прямоугольники.
Площадь каждой частичной области не примыкающей к границе D , будет
равна произведению x y. Поэтому запишем f ( x, y)d f ( x, y)dxdy (*)
D
D
10.
x2При вычислении (*) опираемся на то, что он выражает объем V
цилиндрического тела с основанием D,ограниченного поверхностью
z=f(x.y).
b
Для вычисления V имеет место другая формула, а именно V S ( x)dx (**),
a
где S(x) – площадь поперечного сечения тела плоскостью
перпендикулярной ОХ, а x=a, x=b уравнения плоскостей, ограничивающих
данное тело. Соответствующий рисунок
a
x1
x2
b
Применим эту формулу к вычислению двойного интеграла f ( x, y)dxdy
D
11.
Предположим, что область интегрирования D удовлетворяет следующемуусловию: любая прямая параллельная оси ОХ или оси ОУ пересекает границу
области не более чем в двух точках. Соответствующее цилиндрическое тело
изображено на рисунке
M
N
c
a
A
B
b
d
P
R
C
E
12.
yd
E
x x2 ( y)
y y2 ( x)
R
x x1 ( y)
A
C
P
c
B
a
b
x
y y1 ( x)
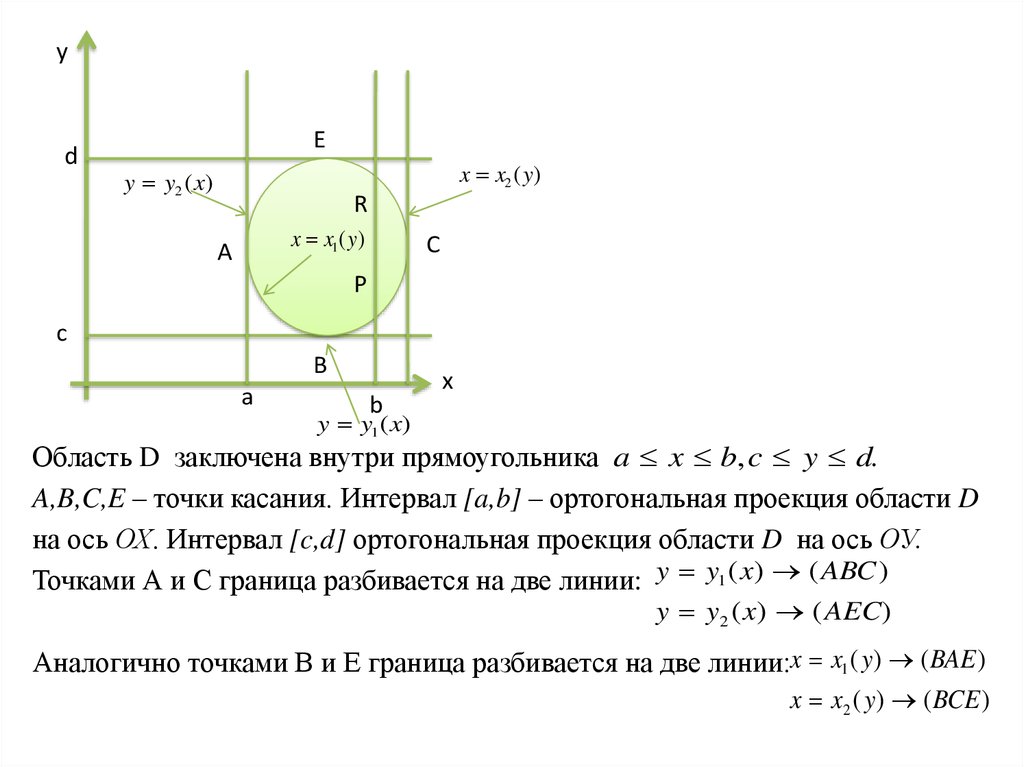
Область D заключена внутри прямоугольника a x b, c y d.
A,B,C,E – точки касания. Интервал [a,b] – ортогональная проекция области D
на ось ОХ. Интервал [c,d] ортогональная проекция области D на ось ОУ.
Точками А и С граница разбивается на две линии: y y1 ( x) ( ABC )
y y2 ( x) ( AEC)
Аналогично точками В и Е граница разбивается на две линии:x x1 ( y) ( BAE )
x x2 ( y) ( BCE )
13.
Рассечем рассматриваемое цилиндрическое тело произвольной плоскостьюпараллельной плоскости OYZ, то есть x=const, где a x b. В сечении
получим криволинейную трапецию PMNR, площадь которой выражается
интегралом от функции f(x,y), рассматриваемой как функция от одной
переменной y, причем y изменяется от ординаты точки P до ординаты точки
R; x=const в области D (P – точка входа, R - точка выхода). Из уравнений
линий ABC и AEC следует, что ординаты этих точек при взятом x
соответственно равны y1 ( x), y2 ( x).
y2 ( x )
Следовательно, интеграл f ( x, y )dy дает выражение для площади плоского
y1 ( x )
сечения PMNR. Ясно, что величина этого интеграла зависит от выбранного
значения х, то есть площадь рассматриваемого
поперечного сечения является
y2 ( x)
некоторой функцией от х. Обозначим S ( x) f ( x, y )dy
y1 ( x )
Согласно формулы (**) объем всего тела будет равен интегралу от S(x) в
интервале изменения x a x b
14.
b y2 ( x)Тогда после замены S(x) выражением, получим V f ( x, y )dxdy [
D
b
Более удобна форма V f ( x, y )dxdy dx
D
a
f ( x, y)dy]dx
a y1 ( x )
y2 ( x)
f ( x, y)dy
(***)
y1 ( x )
Меняя роли х и y, то есть, рассматривая сечение тела
плоскостью y=const
х ( y)
c y d, находим площадь Q(y) такого сечения f ( x, y )dx где y считается
2
x1 ( y )
величиной постоянной. Интегрируя затем Q(y) в пределах интегрирования
второе выражение для двойного интеграла, то есть
c y d получаем
x ( y)
d
V f ( x, y )dxdy dy f ( x, y )dx (****)
D
с
2
x1 ( y )
Формулы (***) и (****) показывают, что вычисление двойного интеграла
сводится к последовательному вычислению двух обыкновенных
определенных интегралов. Нужно помнить, что во внутреннем интеграле
одна из переменных принимается при интегрировании за постоянную
величину.
15.
Правые части формул (***) и (****) называются повторными (илидвухкратными) интегралами – сам процесс расстановки пределов
интегрирования – приведением двойного интеграла к повторному.
Если область D – прямоугольник со сторонами параллельными осям
координат, то есть имеет вид, представленный на рисунке,
то пределы
b
d
d
b
интегрирования – постоянные величины f ( x, y)dxdy dx f ( x, y)dy dy f ( x, y)dx
D
a
c
c
a
В других случаях для сведения двойного интеграла к повторному
необходимо прежде всего построить область интегрирования, удобнее
изображать ее прямо в области ОХУ. Затем нужно установить порядок
интегрирования, то есть определить по какой переменной будет
производиться внутреннее интегрирование, а по какой внешнее, и расставить
пределы. В следующих примерах показано, как производится расстановка
пределов интегрирования.
1. Привести к повторному двойной интеграл
f ( x, y)dxdy , если
D
область D – треугольник, ограниченный прямыми y=o, y=x, x=a.
16.
Если интегрировать сначала по y, а потом по х, то внутреннееинтегрирование производится от линии y=0 до линии y=x, а внешнее от
a
a
a
точки x=0 до точки x=a. Тогда
f ( x, y )dxdy dx f ( x, y )dy dy f ( x, y )dx
D
y
0
0
y
a
y=x
x
a
2. Привести к повторному двойной интеграл
ограниченна линиями y 0, y x 2 , x y 2
f ( x, y)dxdy , если область D,
D
17.
y x2x
B(1,1)
x=2-y
y=2-x
y
y=0
C(1,0)
A(2,0)
x
Как видно из рисунка удобнее интегрировать вначале по х, затем по у
1
2 y
f ( x, y)dxdy dy f ( x, y)dx
D
0
y
Если изменить порядок интегрирования, то необходимо поступить
следующим образом. Линия ОВА представлена двумя
уравнениями. Разбиваем область D на две области: OBC и CBA.
Получаем
1
x2
2
2 x
f ( x, y)dxdy d x f ( x, y)d y dx
D
0
0
1
0
f ( x, y)dy
18.
Формулы (***) и (****) можно использовать и в случае областей болееобщего вида. Так (***) и (****) применимы к областям следующего вида
y y 2 ( x)
d
x x1 ( y)
x x2 ( y)
c
y y1 ( x)
a
b
Области боле сложной формы обычно можно разбить на конечное число
более простых областей и вычислить двойные интегралы по этим простым
областям, используя формулы (***) и (****). Например, таким образом, будет
вычислен двойной интеграл по данной области.
19.
Примеры вычисления двойных интегралов1
1
1. Найти двойной интеграл от функции z 1 3 x 4 по прямоугольной
области D ( 1 x 1; 2 y 2)
I
1
1
(
1
x
D 3 4 y)dxdy
Решение Геометрически I выражает объем четырехугольной призмы,
основанием которой служит прямоугольник D, усеченный плоскостью.
1
1
x
y z 1
3
4
Фигура изображена на следующем рисунке.
z
(-1,2)
у
(1,2)
(1,-2)
х
20.
Вычислим повторный интеграл сначала по у, затем по х1
2
1
1
1 1
1
1 2 2
4
2 2 1
I dx (1 x y )dy ( y xy y ) | 2 dx (4 x)dx (4 x x ) | 1 8
3 4
3
8
3
3
1 2
1
1
Аналогичный результат получаем, интегрируя сначала по х, затем по у
2
1
2
2
1 1
1 2 1
1
1
1
I dy (1 x y )dx ( x x xy ) | 1 dy (2 y )dy (2 y y 2 ) |2 2 8
3 4
6
4
2
4
2 1
2
2
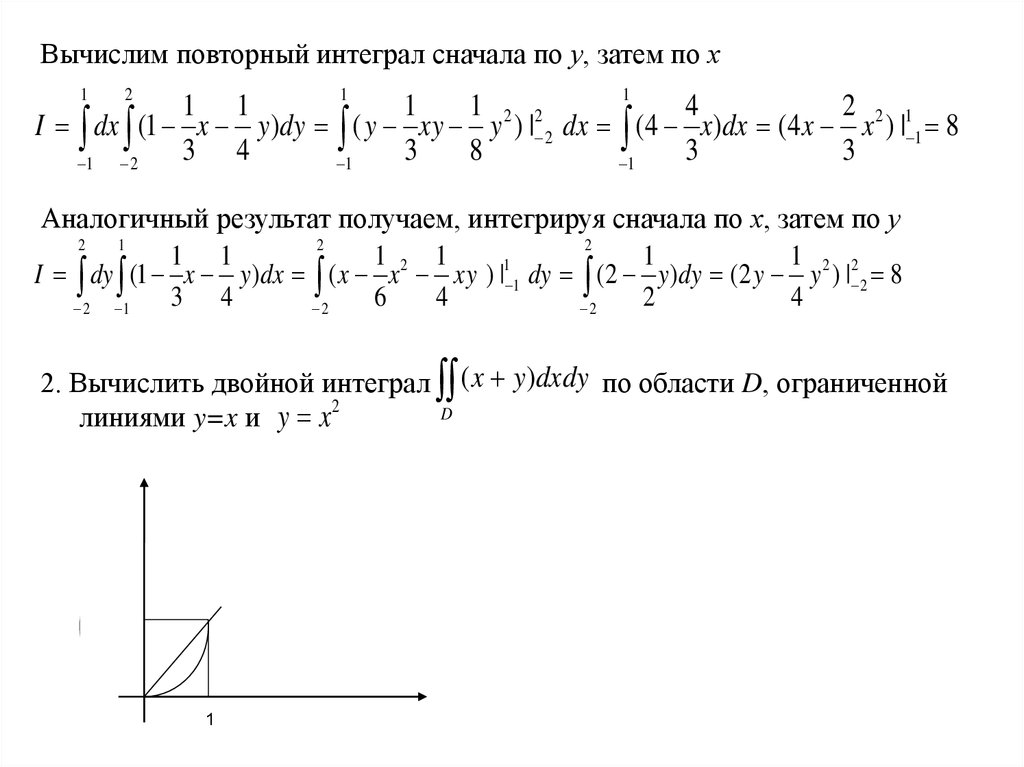
2. Вычислить двойной интеграл ( x y)dxdy по области D, ограниченной
D
линиями y=x и y x 2
1
21.
РешениеА) Интегрируем сначала по у, затем по х
1
x
1
1
y2 x
3x 2 3 x 4
x3 x 4 x5 1 3
D ( x y)dxdy 0 dx 2 ( x y)dy 0 [ xy 2 ] |x 2 dx 0 ( 2 x 2 )dx ( 2 4 10 ) |0 20
x
B) Интегрируем сначала по х, затем по у
5
y
1
1
1
x2
y
3y2
y 2 2 y 2 y3 1 3
y
D ( x y)dxdy 0 dy y ( x y)dx 0 [ 2 xy] |y dy 0 ( 2 y y 2 )dy ( 4 5 2 ) |0 20
3. Вычислить объем тела, ограниченного цилиндрическими поверхностями
x 2 и плоскостью z=0
2
z
z 4 y ,y
2
y
22.
y(-2,2)
(2,2)
y
x2
2
x
Решение
Поверхность, ограничивающая тело сверху имеет уравнение . Область 2
x
y
интегрирования D получается в результате пересечения параболы
2
с линией пересечения цилиндра z 4 y и плоскости z=0, то есть с прямой
y=2. В виду симметрии тела относительно плоскости OYZ вычисляем
половину искомого объема
2
2
2
2
1
y3 2
8
x6
16
2 x3
x 7 2 128
2
2
V dx (4 y )dy (4 y ) | x 2 dx (8 2 x )dx ( x
) |0
2
3
3
24
3
3
168
21
2
0
0
0
x
2
2
V
256
12,2
21
4. Вычислить объем тела, ограниченного поверхностью z 1 4 x 2 y 2
и плоскостью OXY.
23.
Заданное тело – сегмент эллиптического параболоида, расположенного надплоскостью OXY. Параболоид пересекается с плоскостью OXY по эллипсу
4 x 2 y 2 1.
Следовательно, необходимо вычислить объем тела, имеющего своим
основанием внутреннюю часть указанного эллипса и ограниченного
параболоидом. В силу симметрии относительно плоскостей OXZ и OYZ
можно вычислить объем четвертой его части, заключенной в первом октанте.
Область интегрирования 4 x 2 y 2 1, x 9, y 0 (см. рисунок)
Интегрируем сначала по у, затем по х
1
2
1
V dx
4
0
V
4
1 4 x
1
2
2
2
2 1
1 3
2 2
4
(
1
4
x
y
)
dy
(
1
4
x
)
dx
{
2
x
sin
t
}
cos
t
dt
0
3 0
3 2 0
3 16
16
2
2
2
3
24.
Замена переменных в двойном интегралеПолярные координаты
При вычислении определенных интегралов важную роль играет правило
замены переменной, согласно
которому
при соблюдении соответствующих
x
u
условий имеет место f ( x)dx f [ (u )] ' (u )du
2
2
x1
u1
Обычно функция x (u ) монотонна; тогда она осуществляет
взаимнооднозначное соответствие между точками интервала [u1 , u2 ]
изменения переменной u и точками интервала[ x1, x2 ] изменения
переменной х.
Заменяя x (u ) dx ' (u)du, x1 u1, x2 u2 Правило замены
переменной в двойном интеграле достаточно сложное. Приведем формулу
замены.
При переходе в двойном интеграле от переменных x,y к новым переменным
u,v: x=x(u,v), y=y(u,v) (*) формула замены такова.
x x
( x, y )
, где ( x, y ) u v x y x y
f
(
x
,
y
)
dxdy
f
[
x
(
u
,
v
),
y
(
u
,
v
)]
dudv
D
(
u
,
v
)
y
y
(u, v)
u v v u
D
*
x dv
25.
Есть функциональный определитель Якоби (Якобиан) составленный из( x, y)
dudv
частных производных функций (*), то есть d dxdy
(u, v)
Старая область интегрирования D заменяется на новую область D* по
переменным u,v. Новое выражение для называется элементом площади в
координатах u,v.
При удачной замене переменных преобразованный интеграл может оказаться
проще чем исходный, например, пределы интегрирования могут оказаться
постоянными.
y
v
D*
D
x
u
26.
Двойной интеграл в полярных координатахПрименим формулу (**) к преобразованию с помощью полярных координат
(обозначения общепринятые)
x r cos , y r sin , r 0,0 2 ( )
Якобиан будет равен ( x, y) x y x y cos r cos ( r sin ) sin r
(r , )
r
r
Тогда f ( x, y )dxdy f (r cos , r sin )rdrd (***), где D и - соответствующие
D
друг другу области вD плоскостях OXY и O1r (здесь r и рассматриваются
как декартовы координаты точки).
Например, пусть D - полукруг радиуса R, расположенный в полуплоскости
y 0. Во вспомогательной плоскости O1r ему соответствует
прямоугольник 0 r R,0 (здесь точке (0,0) плоскости OXY
соответствует отрезок 0, на оси в плоскости O1r . Это нарушение
взаимной однозначности происходит на границе области D*, при этом
формулы преобразования сохраняются).
Если D - весь круг радиуса R, то ему соответствует прямоугольник
0 r R,0 2
*
27.
y2
R
x
r
Формулу для элемента площади в полярных координатах можно получить из
геометрических соображений. Построим в плоскости OXY координатные
линии для полярной системы координат: r=const, const . Они разбивают
плоскость на криволинейные четырехугольники, ограниченные дугами
концентрических окружностей и их радиусами.
28.
rr
Рассмотрим выделенный четырехугольник.
1
1
1
Его площадь 2 (r r ) 2 2 r 2 r r 2 ( r ) 2
Второе слагаемое – бесконечно малая величина более высокого
порядка, чем первое слагаемое. Отбрасывая его получим
приближенное равенство r r d rdrd , а это приводит к
формуле (***).
29.
Замечание Чтобы привести двойной интеграл в полярных координатах кповторному, обычно нет необходимости строить область D*, во
вспомогательной плоскости O1r , а можно просто руководствоваться
следующими правилами:
1. Пусть полюс содержится внутри области интегрирования D, заключенной
между лучами 1, 2 и линии const встречают ее границу не более
чем в двух точках.
Возможны такие области
r r2 ( )
B
A
E
r r2 ( )
C
r r1 ( )
r r1 ( )
1
2
Полярными уравнениями кривых AEC и ABC пусть будут r r1 ( ), r r2 ( ) .
Обе функции непрерывны в замкнутом интервале 1 , 2 .
30.
Интегрируя сначала по r в пределах его изменения при постоянном , тоесть от r r1 ( ), r r2 ( ) , а затем по от 1 2
2
r2 ( )
1
r1 ( )
получим I d
f (r cos , r sin )rdr
Интегрирование в обратном порядке, то есть сначала по , а затем по r
обычно не встречается.
Если линия ACE (левый рисунок) стягивается в точку 0, то r r1 ( ) 0
В частном случае, когда областью интегрирования служит часть кругового
r1 r r2 , 1 2 кольца пределы интегрирования постоянны по обеим
2
r2
Переменным I d f (r cos , r sin )rdr
1
r1
2. Пусть полюс содержится внутри области интегрирования. Полярный
радиус пересекает границу
в одной точке. Интегрируя сначала по r, затем
r ( )
2
по , получаем I d f (r cos , r sin )rdr , где r r ( ) - полярное
0
0
уравнение границы области.
31.
В частности, когда r r1 ( ) const R , то есть, когда область интегрированияесть круг с центром в полюсе, получаем
2
R
0
0
I d f (r cos , r sin )rdr
Примеры
1. Расставить пределы интегрирования в полярных координатах,
если D – круг x 2 y 2 ax
Решение. Переходя к полярным координатам, получим уравнение окружности
в виде x r cos . Тогда r1 ( ) 0, r2 ( ) a cos . Пределы изменения по
от , .
2 2
Получаем следующий интеграл I
r a cos
a/2
2
a cos
d
0
2
f ( r cos , r sin ) rdr
32.
2. Вычислить объем общей части шара радиуса а и кругового цилиндрарадиуса а/2 при условии, что центр шара лежит на боковой поверхности
цилиндра.
Решение
Система координат расположена следующим образом: ось OZ лежит на
боковой поверхности цилиндра, ось ОХ совпадает с диаметром цилиндра и
радиусом шара. В силу симметрии измеряемого тела относительно
плоскостей OXY и OXZ, можно вычислить четвертую часть объема,
1
заключенного в первом октанте. Получаем V a 2 x 2 y 2 dxdy , где D –
4
D
полукруг, являющийся половиной основания
цилиндра. Удобно преобразовать двойной интеграл к полярным координатам.
Полярное уравнение полуокружности, ограничивающей область D – x r cos
(см. предыдущий пример).
Сначала интегрируем
по r, затем по .
2
1
V a 2 x 2 y 2 dxdy d
4
D
0
3 2
a cos
0
3
2
2 2
(
a
r
)
|a cos d
a 2 r 2 rdr
0
3
0
a
a3 2
4 3 2
2
(
1
sin
)
d
(
)
V
a( )
3 0
3 2 3
3 2 3
2






























 Математика
Математика








