Двойной интеграл: определение, свойства, вычисление в ПДСК

1. Двойные интегралы

ЛЕКЦИЯ 1
Двойной интеграл:
определение, свойства,
вычисление в ПДСК

2.

Задача, приводящая к понятию двойного интеграла
Рассмотрим
понятие цилиндрического
тела (цилиндроида)
Тело, ограниченное
снизу
замкнутой областью D плоскости Oxy,
сверху – непрерывной над D поверхностью z=f(x;y)≥0,
с боков – цилиндрической поверхностью,
образующая которой параллельна оси Oz,
направляющей служит граница области D,
называется цилиндрическим.

3.

Изобразим
z
Непрерывная над D поверхность
цилиндрическое
тело. z=f(x;y)≥0
z = f (x; y)
Образующая
цилиндрической
поверхности,
параллельная
оси Oz
НаправляющаяО
цилиндрической
поверхности –
граница
области D
Замкнутая область D плоскости Oxy
y
D
x
Цилиндрическая
поверхность
Как найти объём цилиндрического
тела?

4.

Разобьём
тело
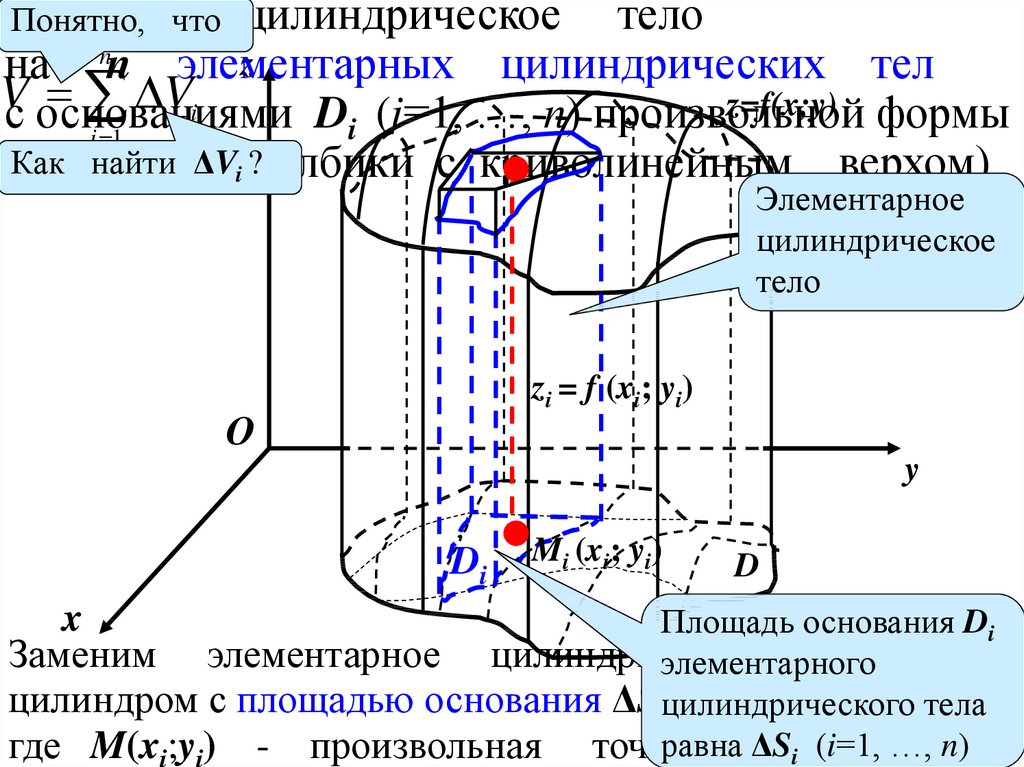
Понятно, что цилиндрическое
z
на nn элементарных
цилиндрических тел
V
Vi
z=f(x;y) формы
с основаниями
D
(i=1,
…,
n)
произвольной
i
i 1
Как найти ΔVстолбики
(получим
с криволинейным верхом).
i?
Элементарное
цилиндрическое
тело
zi = f (xi; yi)
О
y
Di
Mi (xi; yi)
D
x
Площадь основания Di
Заменим элементарное цилиндрическое
тело
элементарного
цилиндром с площадью основания ΔSiцилиндрического
и высотой zi=f(x
тела
i;yi),
равнаDΔS
где M(xi;yi) - произвольная точка
i . i (i=1, …, n)

5.

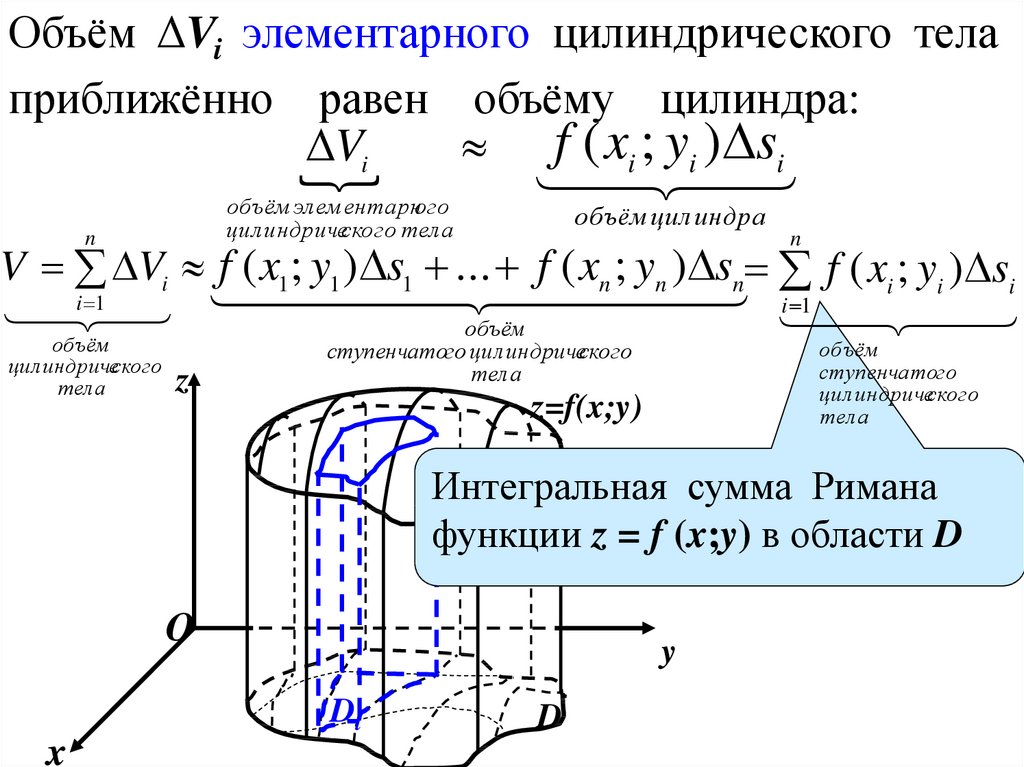
Объём ΔVi элементарного цилиндрического тела
приближённо равен объёму цилиндра:
Vi
f ( xi ; yi ) si
объём элем ентарного
цилиндрического тела
n
объём цил индра
n
V Vi f ( x1 ; y1 ) s1 ... f ( xn ; yn ) sn f ( xi ; yi ) si
i 1
i 1
объём
объём
цилиндрического
тела
z
объём
ступенчатого
цил индрического
тел а
ступенчатого цилиндрического
тела
z=f(x;y)
Интегральная сумма Римана
функции z = f (x;y) в области D
О
y
Di
x
D

6.

Конечный
Определениепредел
двойного
последовательности
интеграла
интегральных сумм I n , I n , …, I n , …,
1
2
k
составленных для различных разбиений области D
и различного выбора точки Mi(xi;yi) в основании Di,
при n и d 0 ( d – наибольшая из хорд
оснований Di), называется двойным интегралом
функции z = f (x; y) по области D:
f ( x; y )ds
D

7.

Рассмотрим значение
каждого символа
Переменные
в обозначении двойного
интеграла:
интегрирования
Область
интегрирования
f ( x; y )ds
Элемент
Другоедвойной
обозначение
двойного
интеграла
Читается:
интеграл
по
области
дэ
эф
икс игрэк дэ эс.
Подынтегральная отплощади
D
cвязано с возможностью
разбиения
области
D
функция
произвольным образом, в том числе и прямыми,
параллельными осям координат:
у
f ( x; y) dxdy
D
площадь
прямоуголь
ника
Di
О
у
х
О
Di y
x
х

8.

Геометрический смысл двойного интеграла:
двойной интеграл функции z = f (x; y) ≥ 0
по области D равен объёму цилиндрического
тела с основанием D, ограниченного сверху
поверхностью z = f (x; y).

9.

Свойства
двойного интеграла
1. (c1 f1 ( x; y) c2 f 2 ( x; y))ds c1 f1 ( x; y)ds c2 f 2 ( x; y)ds
D
D
D
где с1 и с2 - константы
2. Если область интегрирования D разбита на две
непересекающиеся области D1 и D2 такие что
D1 D2 D, то
f ( x; y )ds f ( x; y )ds f ( x; y )ds
D
3.
ds s,
D
D1
D2
где s - площадь области D.

10.

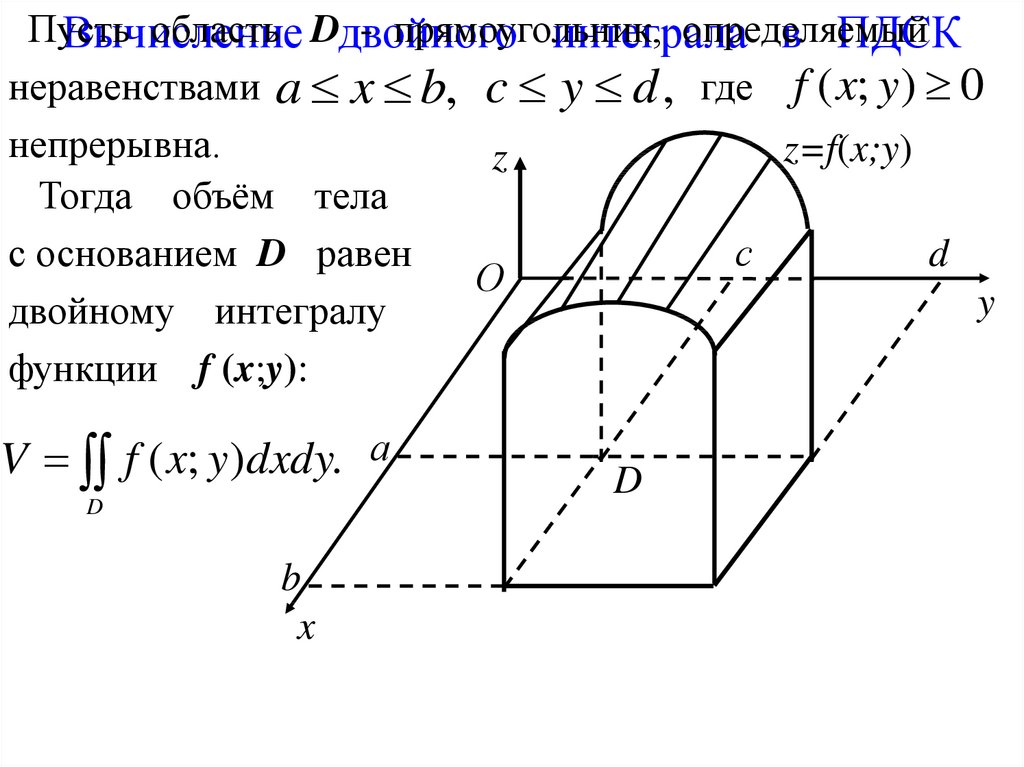
Пусть
область Dдвойного
- прямоугольник,
определяемый
Вычисление
интеграла
в ПДСК
неравенствами a x b, c y d , где f ( x; y) 0
непрерывна.
z=f(x;y)
z
Тогда объём тела
с основанием D равен
с
d
О
y
двойному интегралу
функции f (x;y):
V f ( x; y )dxdy. а
D
b
x
D

11.

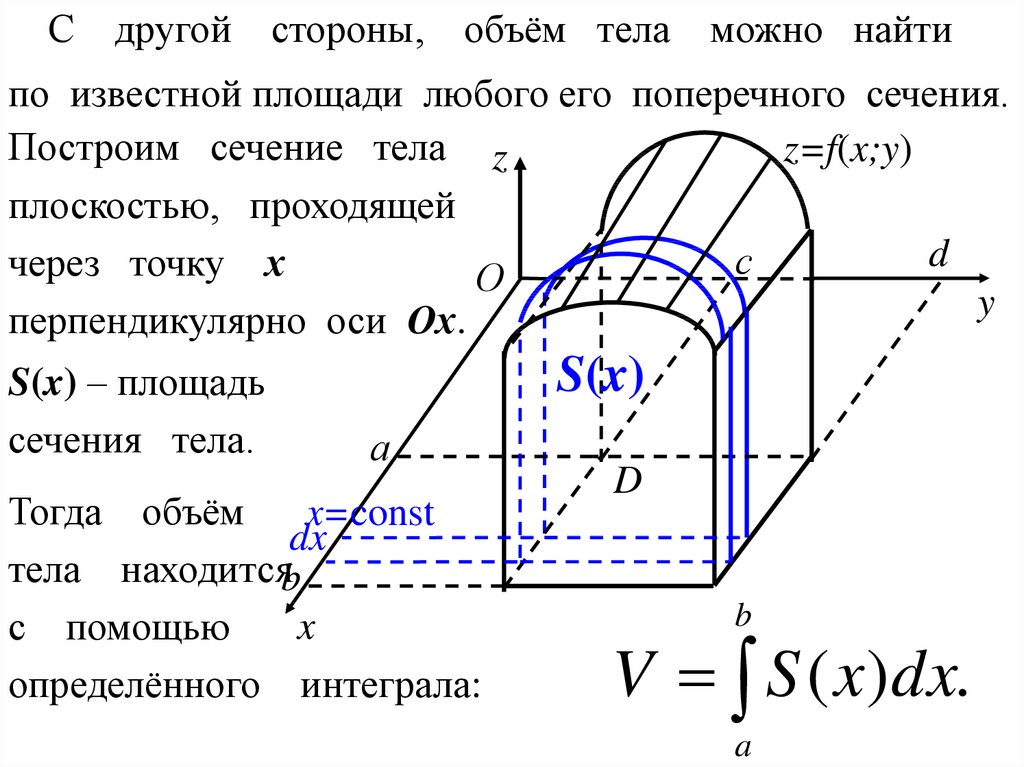
С
другой стороны, объём тела можно найти
по известной площади любого его поперечного сечения.
Построим сечение тела z
z=f(x;y)
плоскостью, проходящей
d
с
через точку х
О
y
перпендикулярно оси Ох.
S(x) – площадь
сечения тела.
S(x)
а
Тогда объём
x=const
dx
тела находитсяb
x
с помощью
определённого интеграла:
D
b
V S ( x)dx.
a

12.

b
Получаем, что
V f ( x; y )dxdy S ( x)dx.
D
Сечением является
z
криволинейная трапеция,
ограниченная сверху
О
графиком функции z=f(x;y),
где значение х
фиксированное,
а
c y d.
x=const
a
z=f(x;y)
с
d
y
S(x)
D
Площадь S(x) b
x
cечения - криволинейной
трапеции d найдём с помощью
определённого интеграла: S ( x) f ( x; y ) dy.
c

13.

b
Тогда V f ( x; y )dxdy S ( x)dx
D
a
f ( x; y )dy dx .
О
a c
b
z=f (x;y)
z
d
повторный интеграл
а
x=const
с
d
y
S(x)
D
b
x
Нахождение двойного
интеграла сводится к вычислению
двух определённых. При вычислении «внутреннего»
интеграла (в квадратных скобках) х считается постоянным.

14.

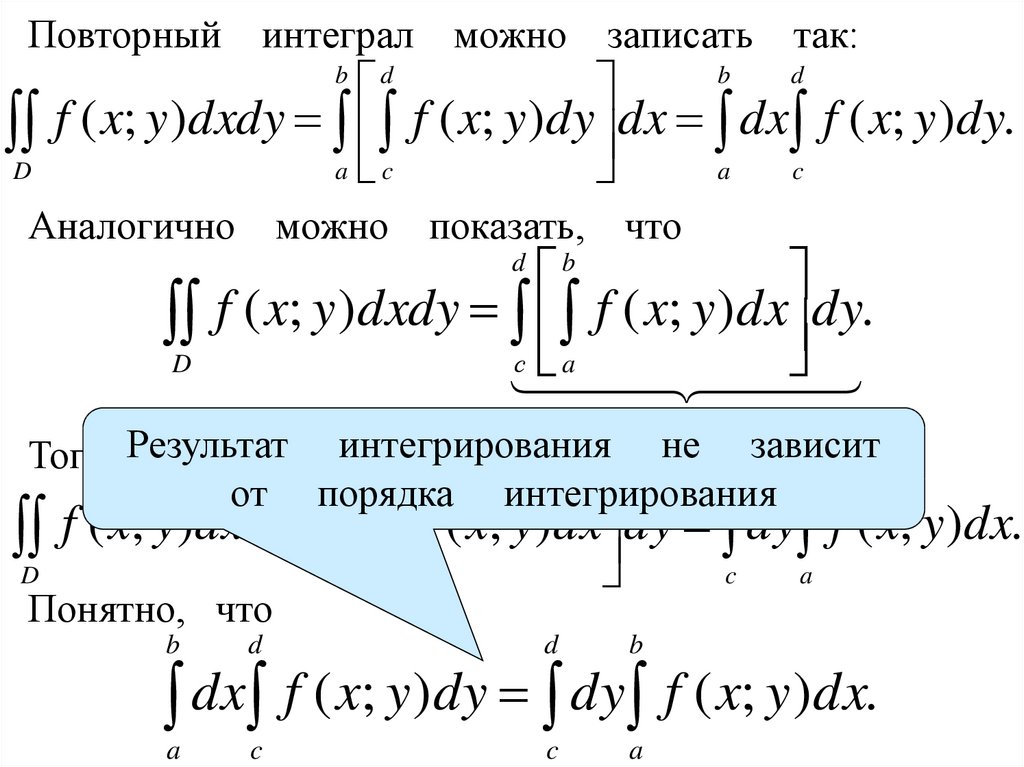
Повторный
D
интеграл можно
записать так:
f ( x; y )dxdy f ( x; y )dy dx dx f ( x; y )dy.
a c
a
c
b
Аналогично
D
d
можно
b
показать,
d
что
f ( x; y )dxdy f ( x; y )dx dy.
с a
d
b
повторный интеграл
не зависит
Тогда Результат интегрирования
d b
d
b
от порядка
интегрирования
f ( x; y)dxdy f ( x; y)dx dy dy f ( x; y)dx.
D
Понятно, что
с
a
c
b
d
d
b
a
c
c
a
a
dx f ( x; y )dy dy f ( x; y )dx.

15.

Пример. Вычислить
( x
2
двойной интеграл
2 y )dxdy,
D
где область D определяется неравенствами
0 x 2,
в
различном
порядке
0 y 1,
интегрирования.

16.

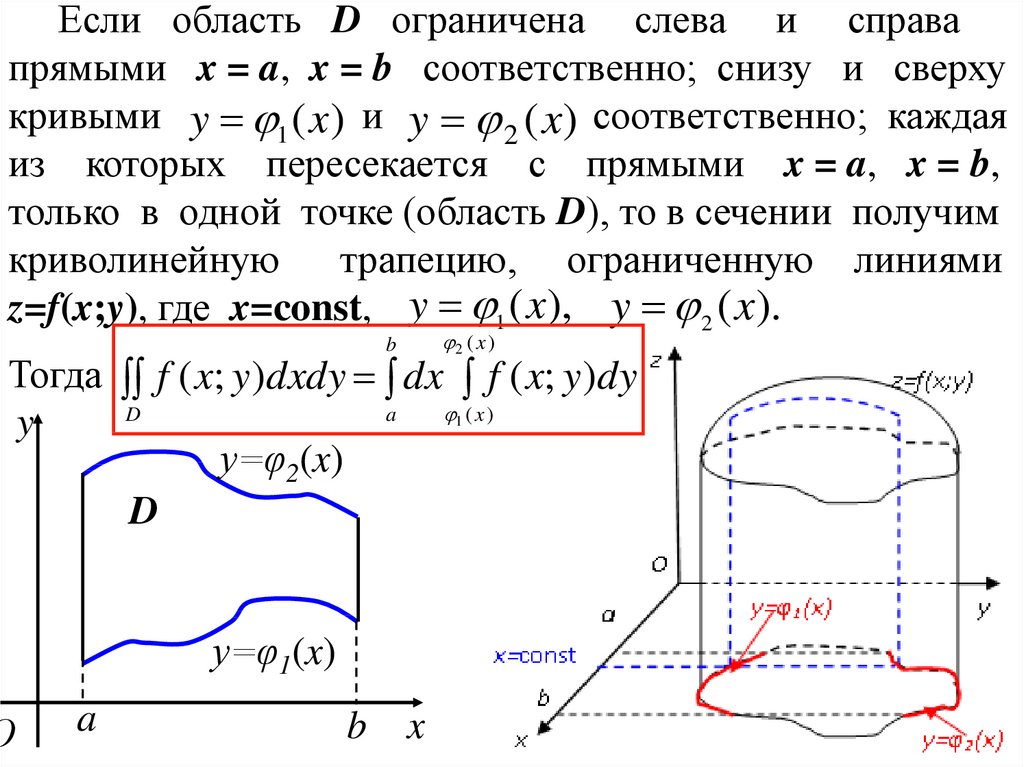
Если область D ограничена слева и справа
прямыми x = a, x = b соответственно; снизу и сверху
кривыми y 1 ( x) и y 2 ( x) соответственно; каждая
из которых пересекается с прямыми x = a, x = b,
только в одной точке (область D), то в сечении получим
криволинейную
трапецию, ограниченную линиями
z=f(x;y), где x=const, y 1 ( x), y 2 ( x).
2 ( x )
b
Тогда f ( x; y )dxdy dx f ( x; y )dy
D
a
( x)
y
y=φ2(x)
D
О
1
y=φ1(x)
a
b
x

17.

Если область D ограничена снизу и сверху
прямыми y = c, y = d соответственно; слева и справа
кривыми x ψ1 ( y ) и x ψ 2 ( y ) соответственно; каждая
из которых пересекается с прямыми y = c, y = d,
только в одной точке (область D), то в сечении получим
криволинейную
трапецию, ограниченную линиями
z=f(x;y), где y=const, x ψ1 ( y ), x ψ 2 ( y ).
Тогда
d
ψ2 ( y )
с
ψ1 ( y )
f ( x; y)dxdy dy f ( x; y)dx
D

18.

Пример. Вычислить
двойной интеграл
(3x 2 y)dxdy,
D
где область D ограничена линиями
y 2x ,
2
y 18.