Геометрическое описание вектора

1.

§7. Векторы
п.1. Геометрическое описание вектора
Вектором называется направленный отрезок.
Обозначается
a, AB
A
B
(если A — начало отрезка, B — конец отрезка).
Вектор BA называется вектором,
противоположным вектору AB,
BA AB.

2.

Длиной (модулем) вектора AB называется
длина отрезка AB.
Обозначается
Вектор
| AB | .
AA
называется нулевым и обозначается
При этом
0.
| 0 | 0.
Нулевой вектор не имеет направления.

3.

Два ненулевых вектора называются
коллинеарными, если они лежат на одной
прямой или параллельных прямых.
Коллинеарные векторы могут быть одинаково
направленными
или противоположно направленными.
Два вектора называются равными, если они
коллинеарные, одинаково направлены и
имеют равные длины.

4.

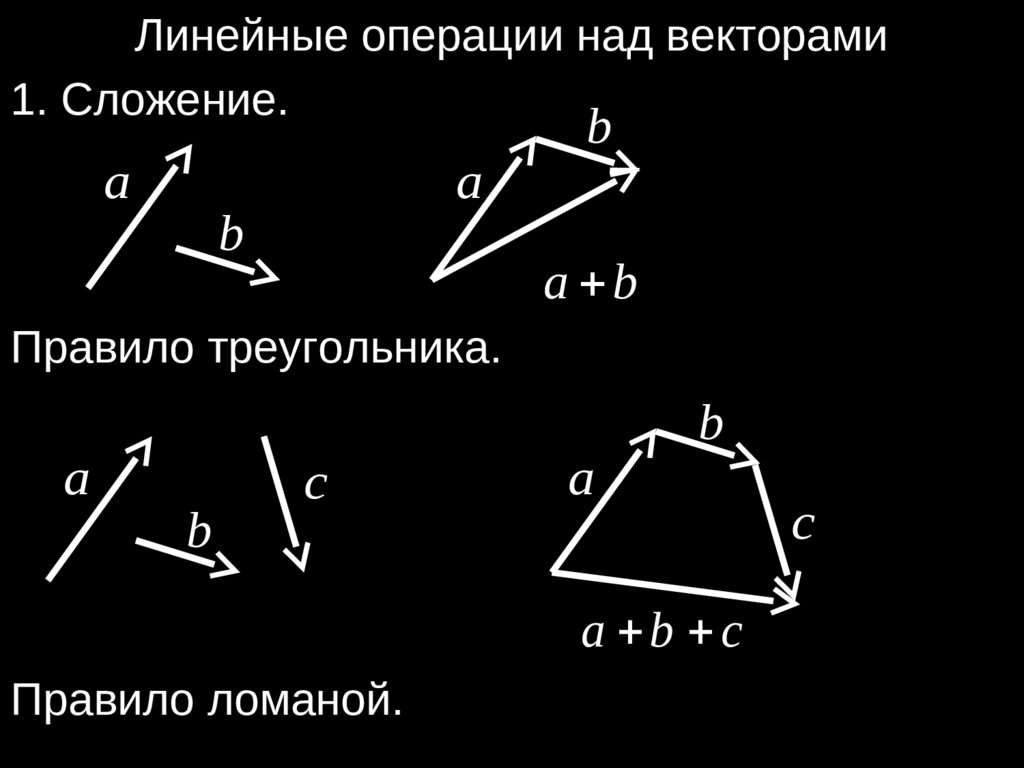
Линейные операции над векторами
1. Сложение.
a
a
b
b
a b
Правило треугольника.
a
b
c
Правило ломаной.
a
b
a b c
c

5.

a
a
b
a b
b
Правило параллелограмма.
2. Вычитание.
a
b
a
b
a b a ( b )
a b

6.

a
a b
a b
b
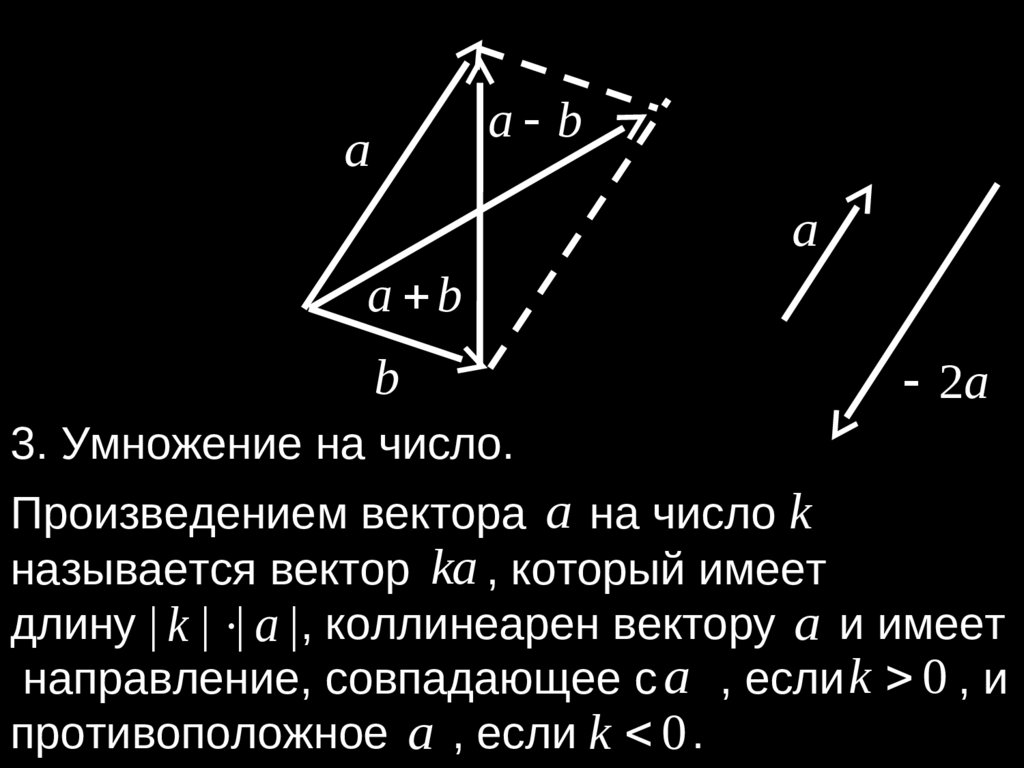
3. Умножение на число.
a
2a
Произведением вектора a на число k
называется вектор ka , который имеет
длину | k | | a | , коллинеарен вектору
и
имеет
a
направление, совпадающее с a , если k 0 , и
противоположное a , если k 0 .

7.

Теорема 1.
Ненулевые векторы a и b коллинеарны тогда
и только тогда, когда существует такое k R ,
что выполняется равенство
b ka.
Причем, если k 0 , то векторы
сонаправлены.
Если k 0 , то векторы противоположно
направлены.

8.

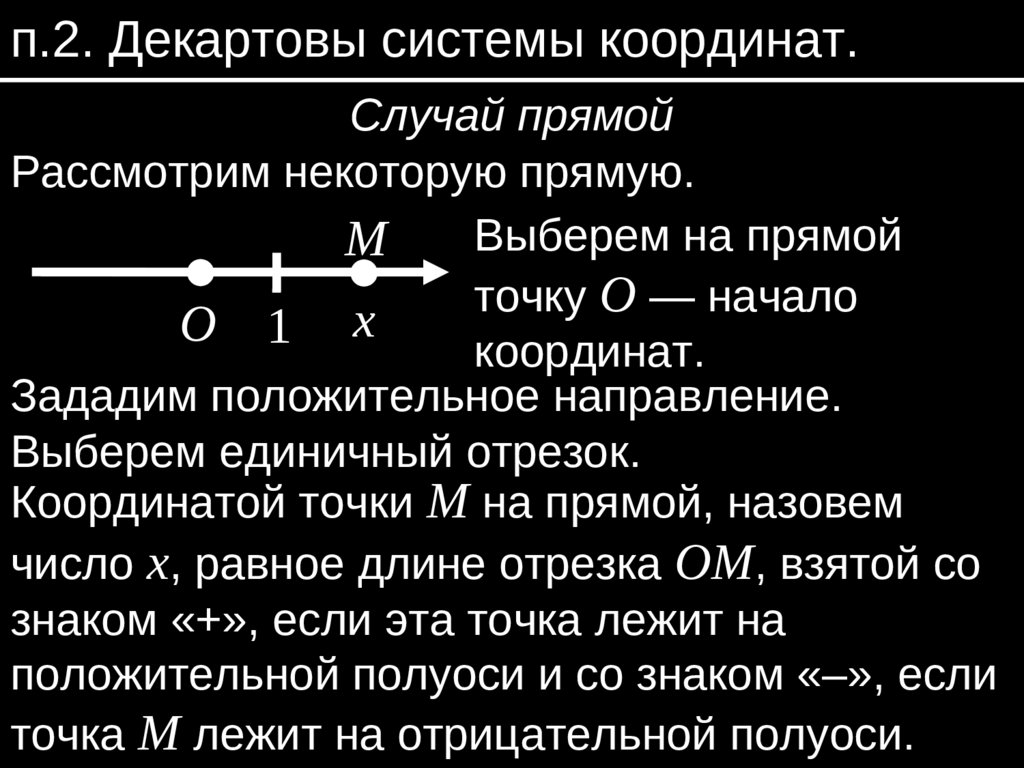
п.2. Декартовы системы координат.
Случай прямой
Рассмотрим некоторую прямую.
Выберем на прямой
M
точку O — начало
O 1 x
координат.
Зададим положительное направление.
Выберем единичный отрезок.
Координатой точки M на прямой, назовем
число x, равное длине отрезка ОМ, взятой со
знаком «+», если эта точка лежит на
положительной полуоси и со знаком «–», если
точка M лежит на отрицательной полуоси.

9.

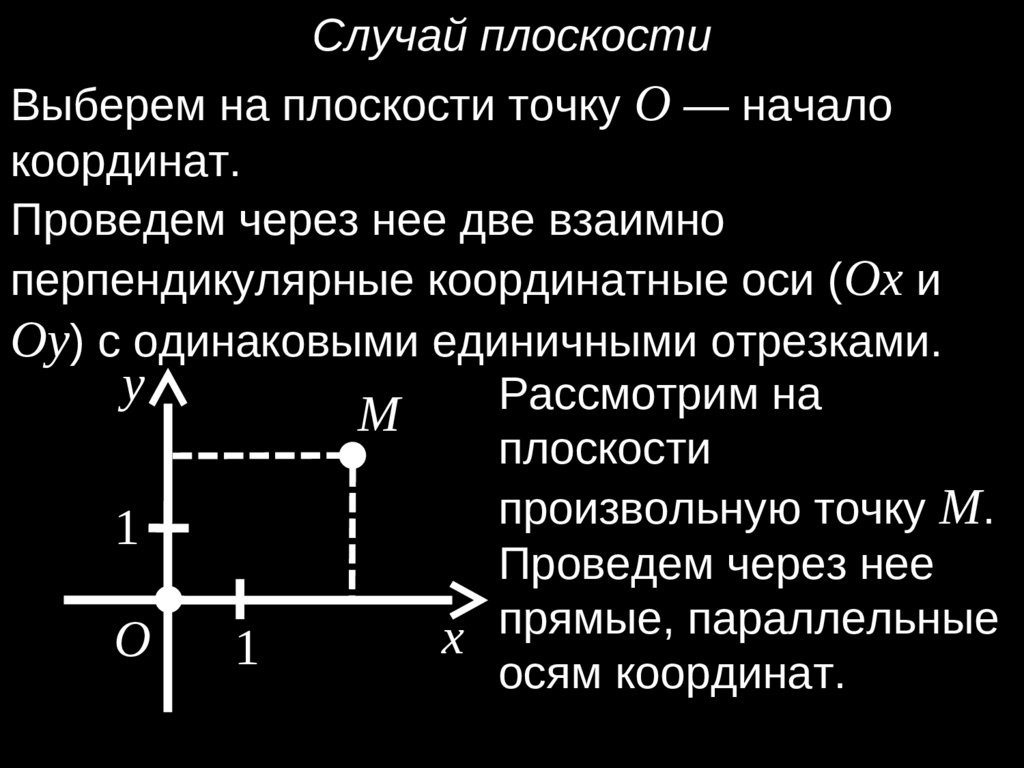
Случай плоскости
Выберем на плоскости точку O — начало
координат.
Проведем через нее две взаимно
перпендикулярные координатные оси (Ox и
Oy) с одинаковыми единичными отрезками.
y
Рассмотрим
на
M
плоскости
произвольную точку M.
1
Проведем через нее
прямые, параллельные
x
O
1
осям координат.

10.

y
My
1
O
M
1
Mx x
Пусть эти прямые пересекают оси координат в
точках M x и M y .
Координата x точки M x называется абсциссой
точки M.
Координата y точки M y называется ординатой
точки M.
M ( x, y ).

11.

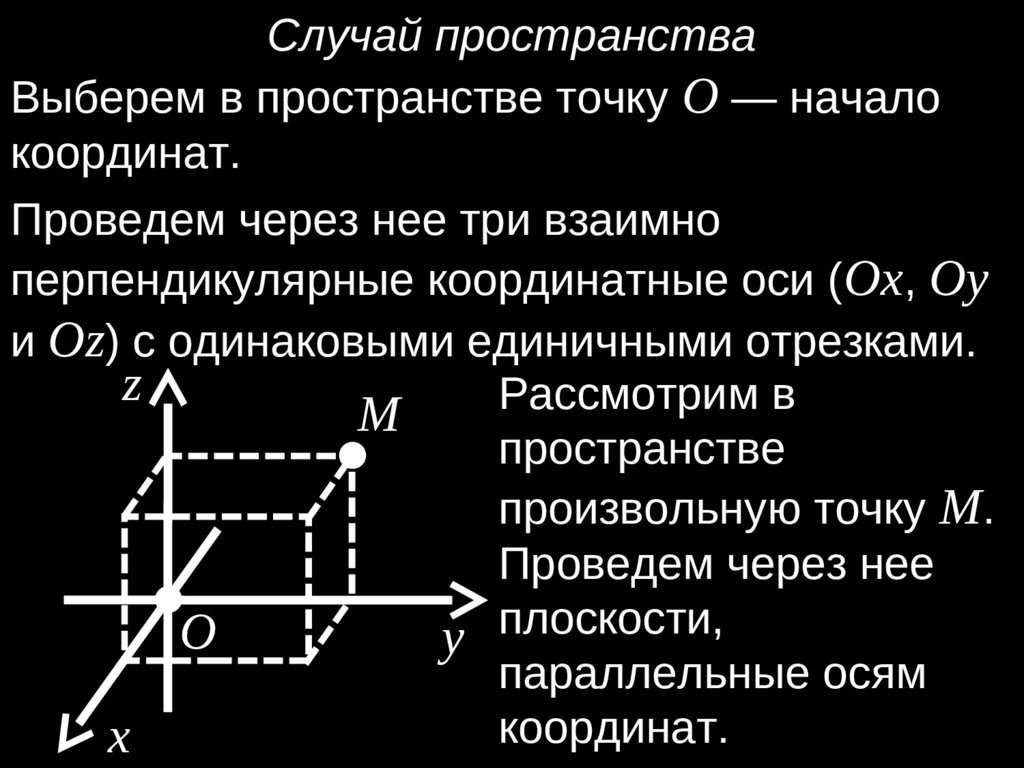
Случай пространства
Выберем в пространстве точку O — начало
координат.
Проведем через нее три взаимно
перпендикулярные координатные оси (Ox, Oy
и Oz) с одинаковыми единичными отрезками.
z
Рассмотрим
в
M
пространстве
произвольную точку M.
Проведем через нее
O
y плоскости,
параллельные осям
координат.
x

12.

z
Mz
Mx
M
O
My y
x
Пусть эти плоскости пересекают оси
координат в точках M x , M y и M z .
Координаты x , y, z точек M x , M y и M z
называются абсциссой, ординатой, и
аппликатой точки M.
M ( x, y , z ).

13.

Замечание.
Часто на плоскости рассматривают полярную
систему координат, а в пространстве
цилиндрическую и сферическую системы
координат.

14.

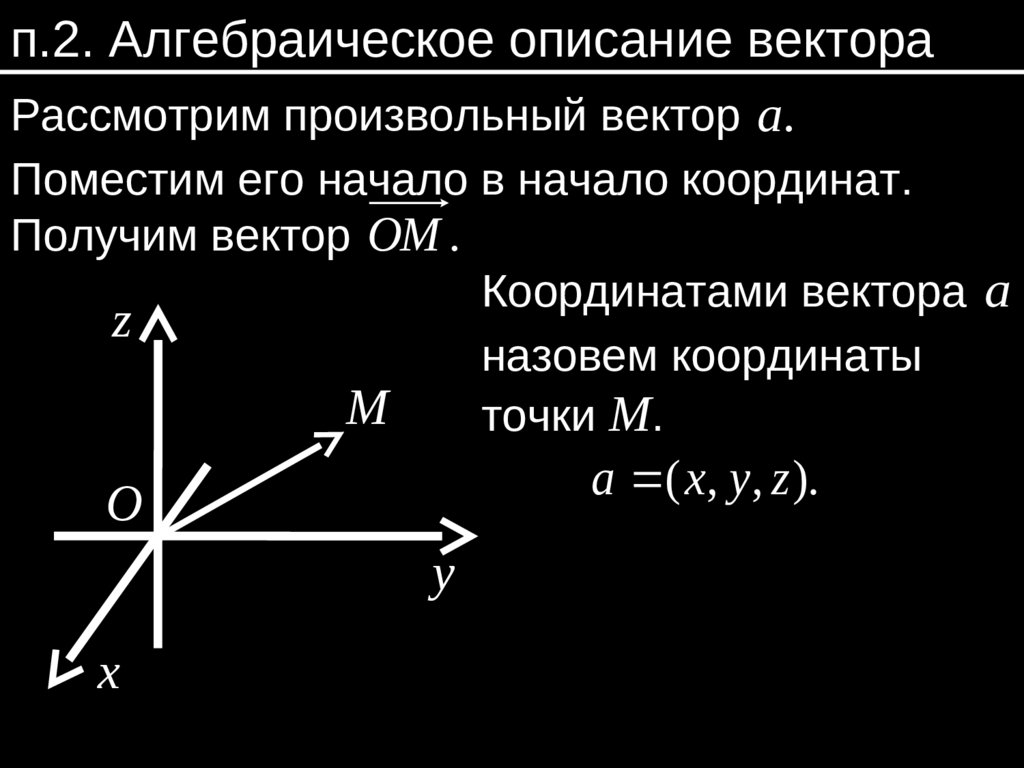
п.2. Алгебраическое описание вектора
Рассмотрим произвольный вектор a.
Поместим его начало в начало координат.
Получим вектор OM .
Координатами вектора a
z
назовем координаты
M
точки M.
a ( x, y, z ).
O
y
x

15.

Замечание.
Между различными векторами пространства и
точками пространства существует взаимно
однозначное соответствие.
Т.е. различным точкам соответствуют
различные векторы и наоборот.
Два вектора называются равными, если они
имеют одинаковые координаты.

16.

Длина вектора
z
M
a
O
Пусть
x
y
a ( x, y , z ).
Тогда | a | равна длине диагонали
прямоугольного параллелограмма, т.е.
| a | x 2 y 2 z 2 .

17.

Линейные операции над векторами
Пусть
a ( x1 , y1 , z1 ), b ( x2 , y2 , z 2 ).
1) Сложение векторов.
a b ( x1 x2 , y1 y2 , z1 z 2 ).
2) Умножение вектора на число.
Если k R , то
ka (kx1 , ky1 , kz1 ).

18.

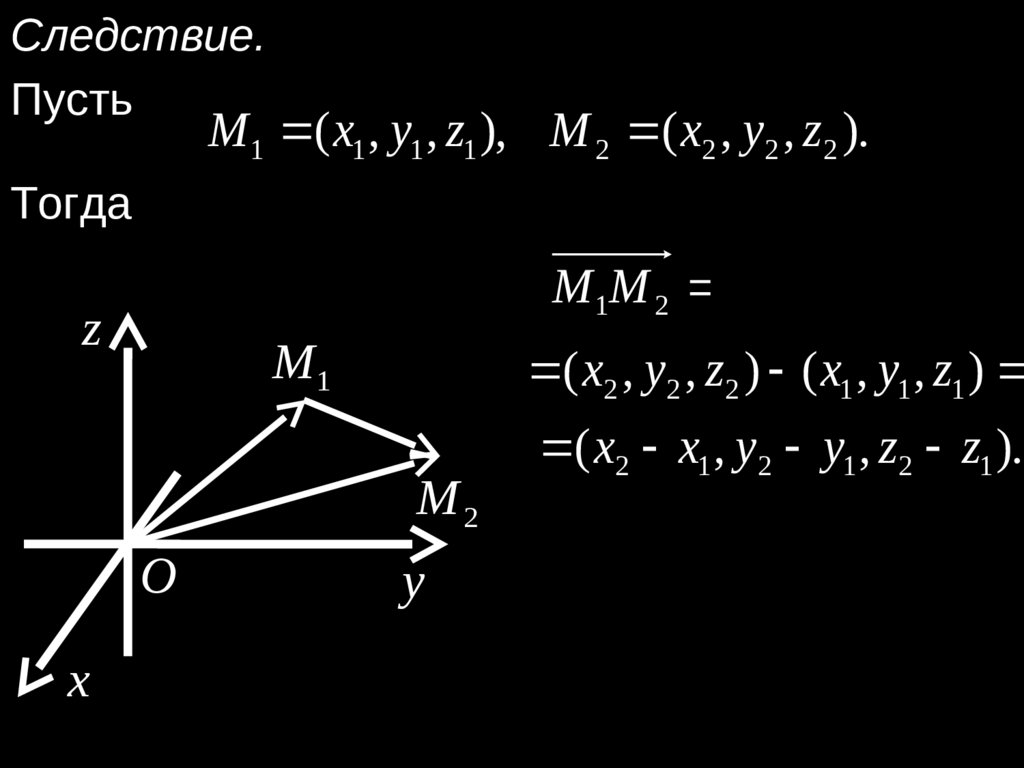
Следствие.
Пусть
M 1 ( x1 , y1 , z1 ), M 2 ( x2 , y2 , z2 ).
Тогда
M 1M 2 OM 2 OM 1
z
M1
( x2 , y2 , z2 ) ( x1 , y1 , z1 )
M2
O
x
y
( x2 x1 , y2 y1 , z2 z1 ).

19.

Теорема 2.
Ненулевые векторы
a ( x1 , y1 , z1 ), b ( x2 , y2 , z 2 ),
коллинеарны тогда и только тогда, когда их
координаты пропорциональны, т.е.
k R
x1 kx2 ,
y1 ky2 ,
z kz .
2
1
Доказательство.
По теореме 1 коллинеарность векторов
равносильна равенству
a kb

20.

или
( x1 , y1 , z1 ) (kx2 , ky2 , kz2 ).
Последнее равенство равносильно системе
x1 kx2 ,
y1 ky2 ,
z kz .
2
1
Замечание.
Если
x 0, y 0, z 0,
2
2
2
то условие коллинеарности можно переписать
x1 y1 z1
в виде
x2
y2
z2
k .

21.

При этом, если k 0 , то векторы
сонаправлены, если k 0 , то противоположно
направлены.
Кроме этого,
|a|
| k | .
|b |

22.

Пример. Пусть
a (7, 2,5), b ( 2,2, 3), c ( 8,6,5), d ( 2,10,3).
Проверить будут ли векторы
a 2b, c d
коллинеарными. Во сколько раз длина одного
из них больше длины второго?
Решение.
a 2 b (7, 2,5) 2( 2,2, 3) (3,2, 1);
c d ( 8,6,5) ( 2,10,3) ( 6, 4,2);
3
2 1
.
6 4 2
Векторы коллинеарны. Длина второго больше
длины первого в 2 раза.