Векторы, линейные операции над векторами, скалярное, векторное, смешанное произведения векторов, условие компланарности векторов

1. Лекция 1. Векторы, линейные операции над векторами, скалярное, векторное, смешанное произведения векторов, условие

компланарности векторов.
1

2.

Векторы. Линейные операции над векторами
Пусть АВ – отрезок. Зададим на нем направление от точки А к точке В.
Такой отрезок называется направленным и обозначается AB .
Вектором (геометрическим вектором) a называется множество всех
направленных отрезков, имеющих одинаковую длину и направление. Всякий
направленный отрезок AB из этого множества также принято называть
вектором, при этом А – начало вектора, В – конец вектора.
Обозначается вектор символами AB или a .
Длиной (модулем) вектора AB называется длина отрезка АВ и
обозначается AB .
Вектор, длина которого равна нулю, называется нулевым вектором и
обозначается 0 . (Нулевой вектор изображается точкой и определенного
направления не имеет).
Два вектора называются равными, если они одинаково направлены и имеют одинаковые
длины, т.е. два вектора AB и CD называются равными ( AB и CD ), если они
представляют один и тот же вектор a .
2

3.

Под линейными операциями над векторами понимают операции сложения и вычитания вектора, а также умножение вектора на число.
Пусть направленный отрезок AB представляет вектор a . Приложив к
точке В заданный вектор b , получим некоторый направленный отрезок BC .
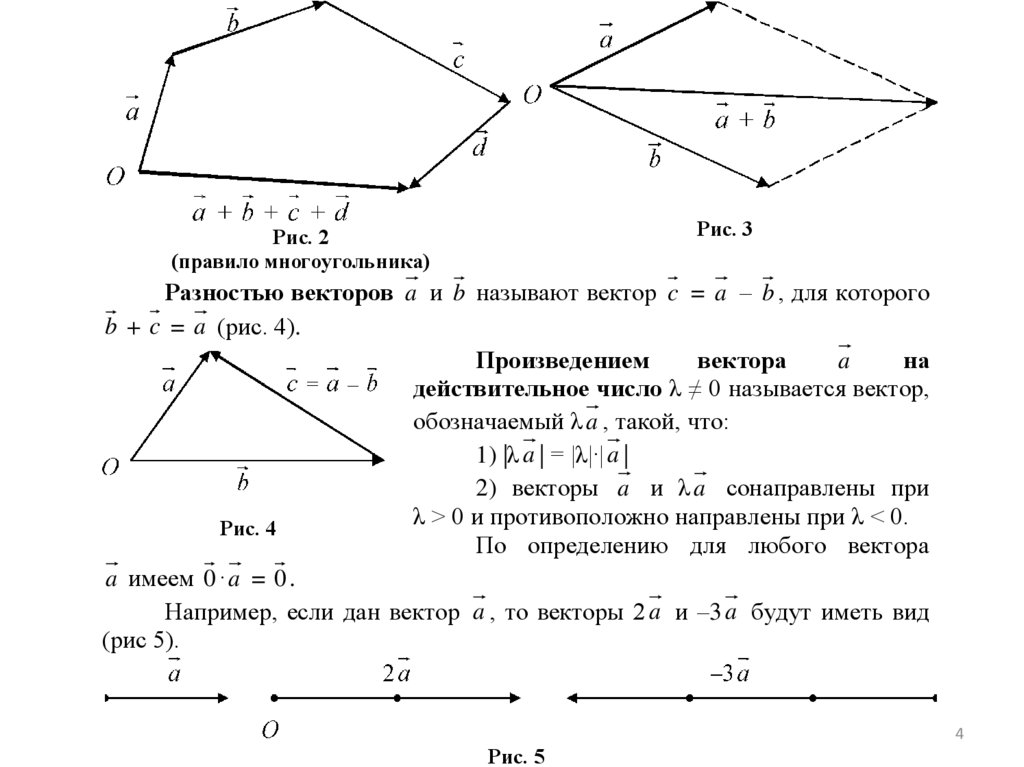
Рис. 1
Вектор, представляемый направленным отрезком AC , называется суммой векторов a и b и обозначается a + b (рис. 1).
Это правило сложения векторов называют правилом треугольника.
Операция сложения может быть распространена на любое число слагаемых векторов (рис. 2).
Сумму двух векторов можно построить также по правилу параллелограмма (рис. 3).
3

4.

Рис. 3
Рис. 2
(правило многоугольника)
Разностью векторов a и b называют вектор c = a – b , для которого
b + c = a (рис. 4).
a
Произведением
вектора
на
действительное число λ ≠ 0 называется вектор,
обозначаемый λ a , такой, что:
1) |λ a | = |λ|·| a |
2) векторы a и λ a сонаправлены при
λ > 0 и противоположно направлены при λ < 0.
Рис. 4
По определению для любого вектора
a имеем 0 · a = 0 .
Например, если дан вектор a , то векторы 2 a и –3 a будут иметь вид
(рис 5).
4
Рис. 5

5.

Скалярное произведение векторов
Скалярным произведением двух ненулевых векторов a и b называется число, равное произведению длин этих векторов на косинус угла φ между
ними:
( a · b ) = | a |·| b |·cosφ.
По определению для любого вектора a ( 0 · a ) = ( a ·0 ) = 0.
Если векторы a и b представлены своими координатами a = (x1; x2; x3)
b = (y1; y2; y3),
то скалярное произведение вычисляется по формуле:
( a · b ) = x1y1 + x2y2 + x3y3.
Из этих формул, в частности, следует формула для определения косинуса угла между векторами:
a b
x1 y1 x2 y2 x3 y3
=
.
cos a,b =
2
2
2
2
2
2
x1 x2 x3 y1 y2 y3
a b
5

6. Векторное произведение. Определение. Свойства.

Определение. Упорядоченная тройка
некомпланарных векторов
называется
правой,
если из конца
вектора с кратчайший поворот
от a к b кажется происходящим против
часовой стрелки. В противном случае тройка
левая.
ab c ; b c a ; c ab; ac b ; c b a ; b a c .
Если есть две тройки либо обе правые, либо обе
левые, то они называются одной ориентации.
6

7.

Определение 1. Векторным
произведением
a b
называется третий вектор c, который
удовлетворяет трем условиям:
1. c a b sin( a, b ) a b sin , 0
c a
2.
c b
3. Векторы a , b , c образуют
правую
тройку.
Обозначают: : a b или: [ a , b ] ,
7

8.

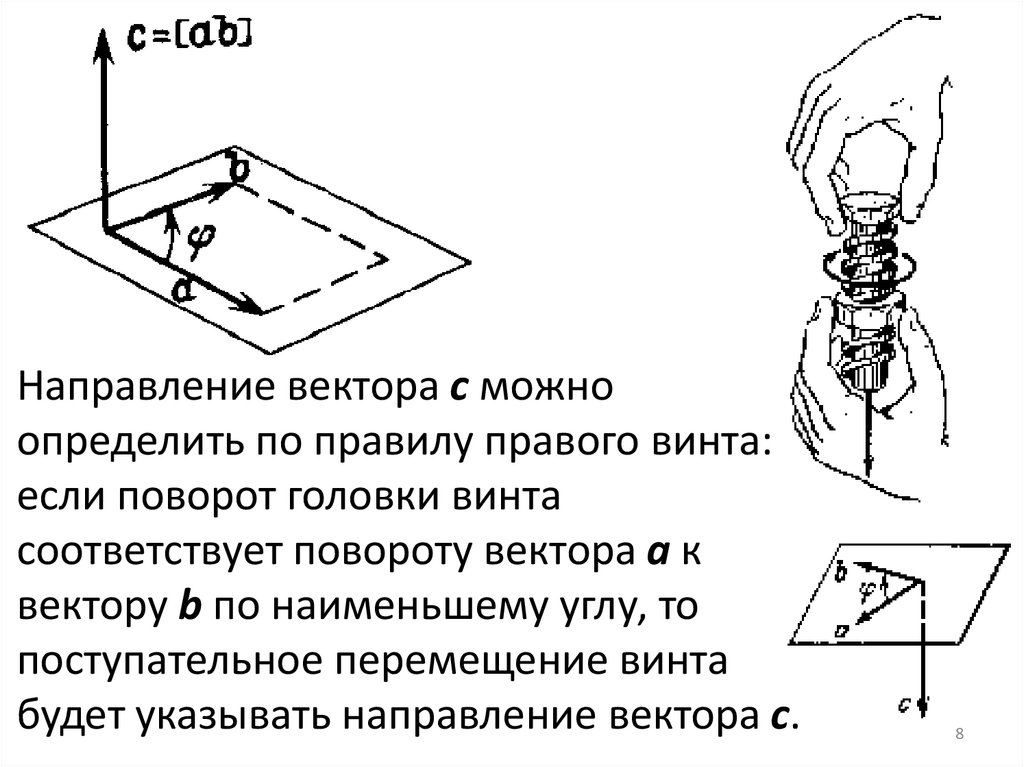
Направление вектора с можно
определить по правилу правого винта:
если поворот головки винта
соответствует повороту вектора а к
вектору b по наименьшему углу, то
поступательное перемещение винта
будет указывать направление вектора с.
8

9.

Замечание: Определение
1
однозначно
определяет вектор c в том случае, если не один
из множителей не равен 0.
В
случае,
если
хоть
один
множитель = 0 , то a , b , c - коллинеарны и
[a , b ] - равно нулевому вектору.
Геометрические свойства векторного
произведения
Теорема 1. Для того чтоб a и b были
коллинеарны необходимо
чтоб их векторное
произведение a b равнялось нулевому
вектору .
9

10.

Доказательство
Необходимость. Пусть a b a b 0 (по
определению 1).
Достаточность . Пусть a b 0 a b 0 .
Из определения 1 a 0 , либо b 0 ,
либо sin( ) 0 .
а) a 0 , b 0 sin( ) 0 a b
б) пусть хотя бы один из a и b нуль тогда
указанный вектор нулевой, он не имеет
определенного направления, следовательно, его
можно считать коллинеарным любому вектору.
10

11.

Теорема 2. Модуль векторного произведения
равняется площади
параллелограмма,
построенного на a и b , как на сторонах.
Действительно, из определения 1 следует:
a, b a b sin( ) S
параллелограмма ab
1
Следствие: S
a, b
ab
2
11

12.

Алгебраические свойства векторного
произведения
1) Антипереместительное a, b a, b b, a
2) Сочетательное свойства относительно
скаляра (ассоциативность)
a, b и R a, b a, b a, b
3) Распределительное свойство относительно
суммы (дистрибутивность)
a, b , c a b , c a, c b , c
Д/З: доказать одно из свойств!
12

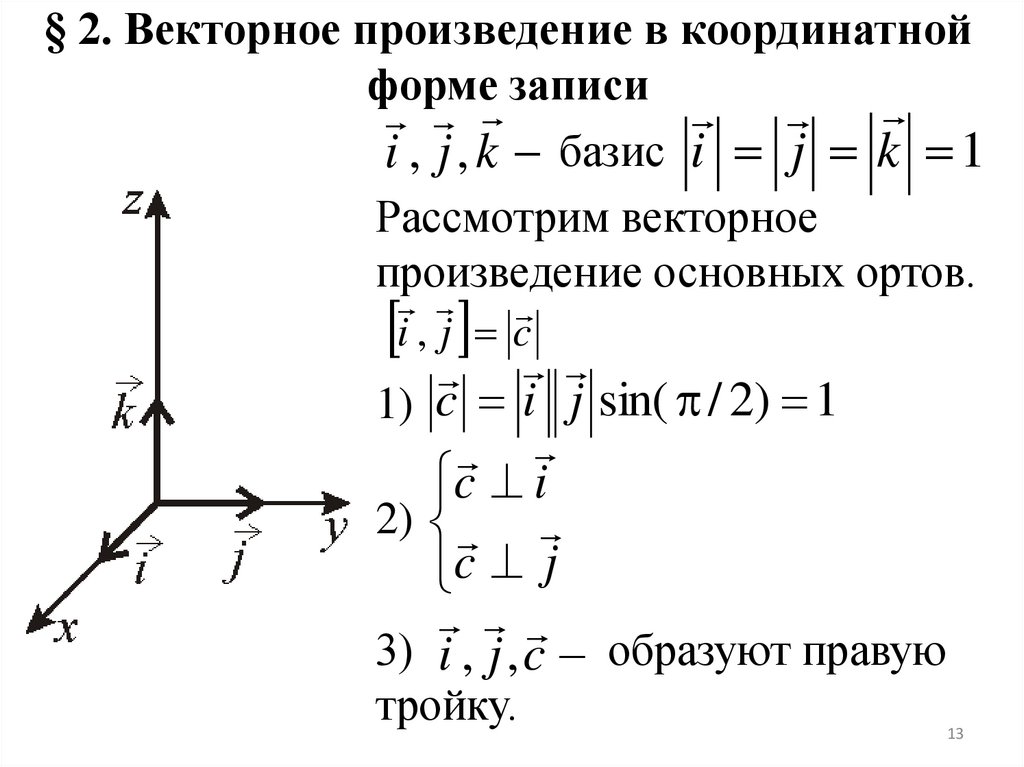
13. § 2. Векторное произведение в координатной форме записи

i , j , k базис i j k 1
Рассмотрим векторное
произведение основных ортов.
i , j c
1) c i j sin( / 2) 1
c i
2)
c j
3) i , j , c образуют правую
тройку.
13

14.

Итак c k ,
i , j k , j , i k
j , k i , k , j i
k ,i j, i ,k j
Пусть в прямоугольной декартовой системе
координат XOYZ
a x1 , y1 , z1
a x1 i y1 j z1 k
или
b x2 , y2 , z2
b x2 i y2 j z2 k
14

15. По распределительному свойству и можно перемножать по правилу многочленов. По сочетательному свойству (2) можно выносить

По распределительному свойству a и b можно
перемножать по правилу многочленов.
По сочетательному свойству (2) можно
выносить постоянный множитель за знак
векторного произведения.
По антипереместительному свойству при
перестановке сомножителей следует изменять
знак
a, b ( x i y j z k ) ( x i y j z k )
x x i,i x y j, i x z k , i x y i , j
y y j, j y z k , j x z i , k y z j, k z z k , k
1
1 2
1 2
1
1
2 1
2 1
2
2 1
1 2
2
2
1 2
1 2
1 2
15

16.

a , b x2 y1 k x2 z1 j x1 y2 k y2 z1 i x1 z 2 j y1 z2 i
a , b i ( y1 z 2 y2 z1 ) j ( x1 z 2 x2 z1 ) k ( x1 y2 x2 y1 ) (**)
a b
y1 z1
y2 z 2
i
x1 z1
x2 z 2
j
x1 y1
x2 y 2
k
i j k
или a b x1 y1 z1
x2 y 2 z 2
Раскрывая символический определитель
третьего порядка по элементам
1-ой строки мы
получим координаты a , b в форме (**)
16

17. § 3. Условие колинеарности двух векторов в координатной форме

Пусть a x1, y1, z1 b x2 , y2 , z2 a, b 0
Значит все три координаты этого вектора в
соотношении (**) - нули. То есть
x1 y1
x1 y2 x2 y1 0
x2 y2
y1 z1
x1 y1 z1
y1 z2 y2 z1 0
,
y2 z2 x2 y2 z2
x1 z1
x1z2 x2 z1 0
x2 z2
то есть если a коллинеарен b , то их
одноимённые координаты пропорциональны.
17

18.

§ 4. Смешанное произведение трёх векторов
Определение. Смешанным или векторно-
скалярным произведением трёх векторов a, b , c
называют число, равное
скалярному
произведению a , b на c и обозначается a , b c
Геометрический смысл смешанного
произведения
Теорема. Смешанное произведение
трёх
некомпланарных векторов a , b , c равно объему
параллепипеда , построенного на этих векторах
как на ребрах, взятому со знаком
«+» , если ab с
- правая и со знаком «-» если ab с - левая тройка
18

19.

Доказательство
правая тройка
левая тройка
a, b c a, b c cos
а) ab c правая a, b c a, b c cos S ab H Vпар
H
б )ab c левая.H c cos c cos( ) c cos
a, b c a, b ( H ) S H V
19

20.

Следствие 2. a, b, c a, b c a b, c
Следствие 1. Vпар a, b c
То есть в смешанном произведении безразлично
какие из векторов перемножаются векторно,
лишь бы не нарушить порядок сомножителей abc
§ 5. Условие компланарности трёх векторов
Для того чтобы a, b, c были компланарными,
необходимо и достаточно: a, b c 0
Доказательство
Достаточность. Пусть a, b, c - компланарны.
20

21.

По определению 1:
a, b a a, b
a, b b
a, b c a, b c 0 ч.т.д.
Необходимость. Пусть a, b c 0
a
,
b
a
По опреде
лению 1:
a, b b a, b aЧ.т.д.
,b,c
Так как их a, b c
скалярное произведение = 0
21

22. § 6. Смешанное произведение в координатной форме

Теорема. Если a, b, c заданы в прямоугольной
декартовой системе координат своими
координатами
a x1 , y1 , z1
b x2 , y2 , z2
c x3 , y3 , z3
то их смешанное произведение
равняется определителю 3-го порядка, строками
которого являются координатные строки
данных векторов.
22

23. Доказательство.

Известно:
Доказательство.
y1 z1 x1 z1 x1
a, b i
j
k
y2 z 2
x2 z2
x2
ñ x3 , y3 , z3
y1
y1
x1 z1
x1
y1 z1
a, b c
x3
y3
y2 z 2
x2 z2
x2
x3 y3 z3
y2
y2
z3
x1 y1 z1
a, b c x1 y1 z1
abc a, b c x2 y2 z2
x2 y2 z2
x3 y3 z3
Ч.т.д.
23