Метод координат в пространстве

1. Метод координат в пространстве

2.

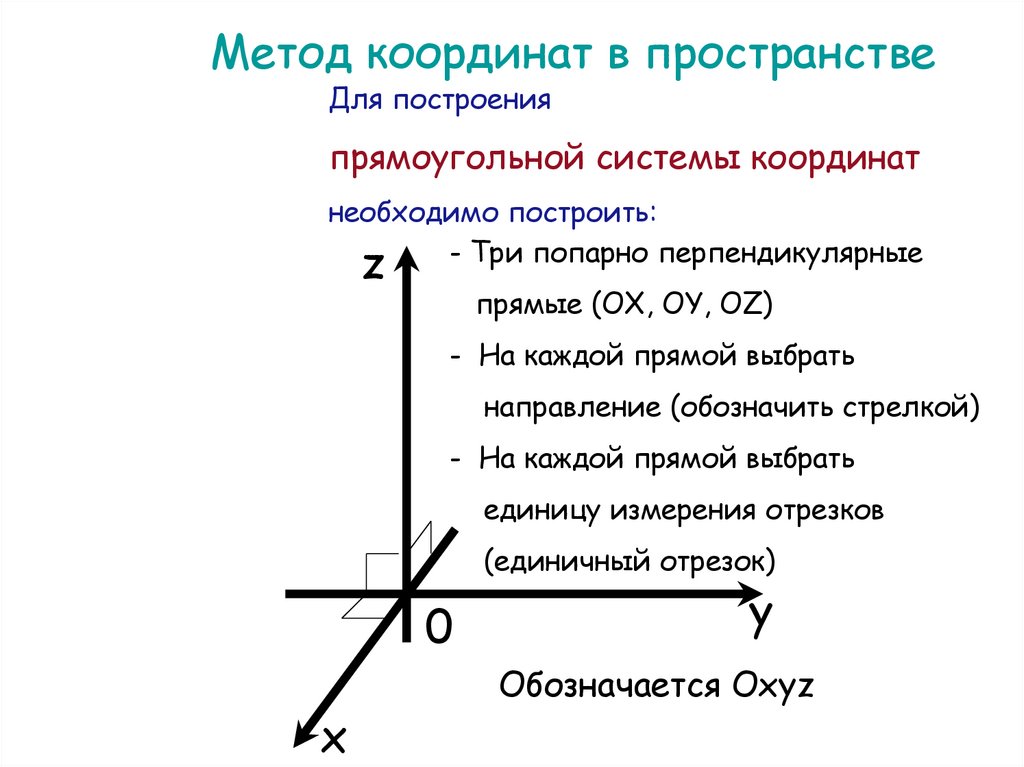
Метод координат в пространстве
Для построения
прямоугольной системы координат
необходимо построить:
- Три попарно перпендикулярные
z
прямые (OX, OY, OZ)
- На каждой прямой выбрать
направление (обозначить стрелкой)
- На каждой прямой выбрать
единицу измерения отрезков
(единичный отрезок)
0
x
y
Обозначается Oxyz

3.

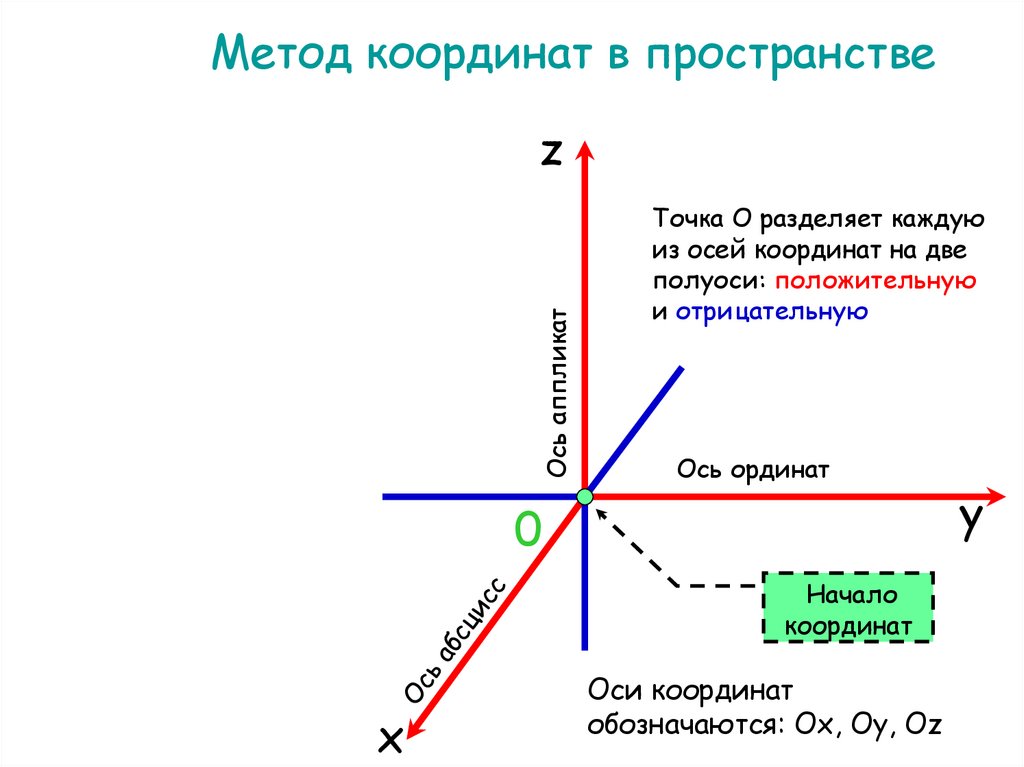
Метод координат в пространстве
Ось аппликат
z
Точка О разделяет каждую
из осей координат на две
полуоси: положительную
и отрицательную
Ось ординат
0
Начало
координат
x
Оси координат
обозначаются: Ox, Oy, Oz
y

4.

Метод координат в пространстве
Проведем
плоскости
перпендикулярные осям
координат,
точки
пересечения с
осями
называются
координатами
данной точки
z
М3
М
0
М1
y
М2
Обозначается:
М(М1;М2;М3), где
x
М1 – абсцисса,
М2 - ордината,
М3 – аппликата.

5.

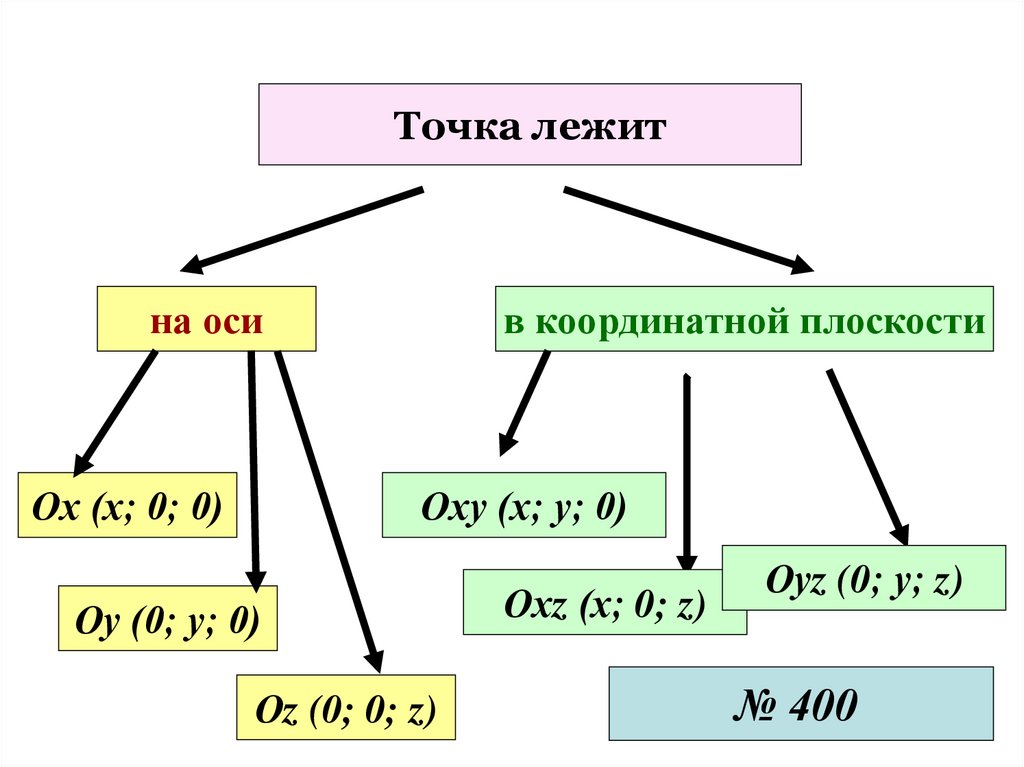
Точка лежит
на оси
Ох (х; 0; 0)
в координатной плоскости
Оху (х; у; 0)
Оу (0; у; 0)
Оz (0; 0; z)
Охz (х; 0; z)
Оуz (0; у; z)
№ 400

6.

Разложение вектора по трём
некомпланарным векторам
Любой вектор а можно разложить по
координатным векторам, т.е. представить в
виде
а = хi + уj + zk ,
причем коэффициенты разложения x, y, z
определяются единственным образом.
Коэффициенты x, y, z в разложении вектора
а по координатным векторам называются
координатами вектора а в данной системе
координат.

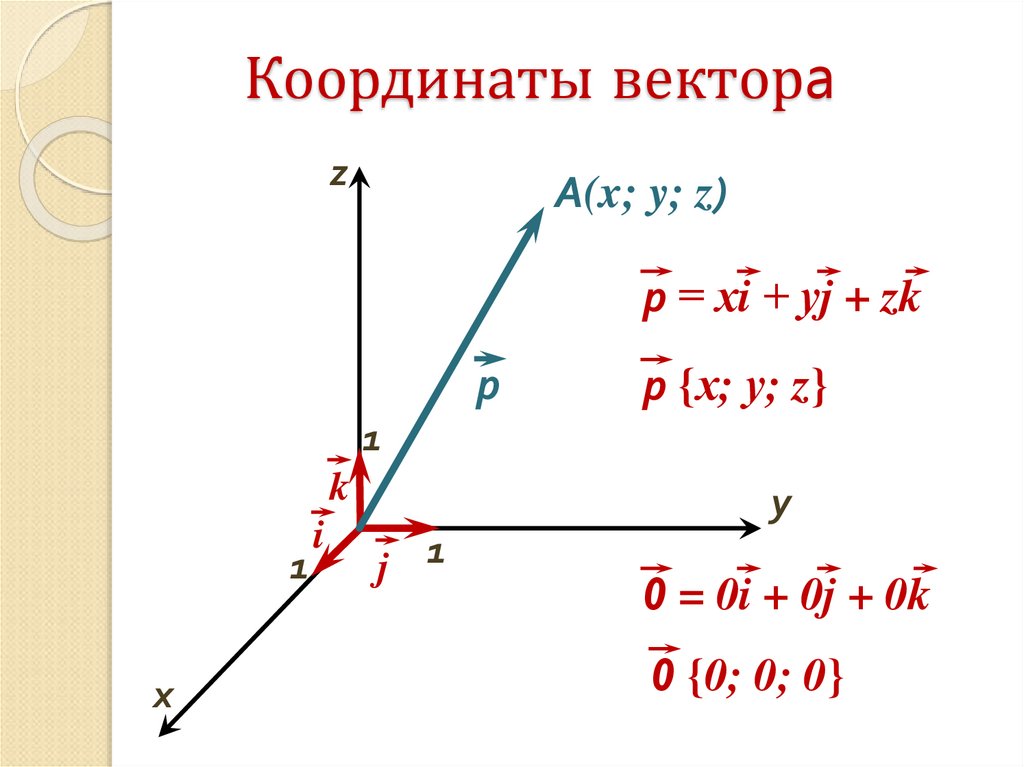
7. Координаты векторa

z
A(x; y; z)
р = хi + уj + zk
р
р {х; у; z}
1
k
1
x
i
y
j 1
0 = 0i + 0j + 0k
0 {0; 0; 0}

8. Действия над векторами

а {х1; у1; z1}
b {х2; у2; z2}
1. Каждая координата суммы двух или более
векторов равна сумме соответствующих
координат этих векторов.
а + b { х1 + x2; у1 + y2 ; z1 + z2}
2. Каждая координата разности двух векторов
равна разности соответствующих
координат этих векторов.
а – b { х1 – x2; у1 – y2 ; z1 – z2}

9. Действия над векторами

а {х1; у1; z1}
3. Каждая координата произведения вектора на
число равна произведению соответствующей
координаты вектора на это число.
kа { kх1; kу1 ; kz1}

10. Связь между координатами вектора и координатами его начала и конца

АВ {х2 – x1; у2 – y1; z2 – z1}
В(x2; y2; z2)
АВ
A(x1; y1; z1)