Математический аппарат динамических систем

1.

Математический аппарата динамических систем
Матрицы полезны при записи и решении линейных алгебраических уравнений.
Рассмотрим, к примеру, систему уравнений
2 x1 x2 x3 4
(1.1)
x1 x2 x3 1
2 x1 x2 3 x3 6
Эти уравнения можно записать в векторно-матричной форме
2 1 1 x1 4
1 1 1 x 1
2
2 1 3 x 6
3
(1.2)
Введем следующие обозначения:
x1
2 1 1
4
A 1 1 1 ; x x2 ; u 1 .
2 1 3
6
x
3
(1.3)
Тогда уравнение (1.2) можно записать в компактной форме:
Ax u.
(1.4)

2.

В этом уравнении A есть матрица размерностью 3˟3 (три строки и 3 столбца), x есть
матрица размерностью 3˟1, u – также матрица размерностью 3˟1. В общем случае матрица
имеет размерность m˟n (m строк и n столбцов). Если m или n равно единице, то такую
матрицу часто называют вектором, таким образом, вектор – это матрица, состоящая либо
из одной строки, либо из одного столбца. Если m и n равны единице, то мы имеем дело со
скалярной величиной. В предыдущих уравнениях, например x и u являются векторами, а ,
скажем x1 – скаляром.
В Matlab матрица A задается одной инструкцией:
В общем виде матица А записывается в виде
a11
A
a
m1
a1n
,
amn
(1.5)
где через aij обозначен элемент, принадлежащий i-й строке и j-му столбцу. Элемент вектора
обычно помечается одним индексом, указывающим его принадлежность соответствующей
строке или столбцу.

3.

Диагональная матрица. Диагональной матрице называется такая квадратная
матрица размерностью (n˟n), в которой все элементы aij = 0 при i≠j; то есть, все
элементы матрицы, расположенные не на главной диагонали, равны нулю.
Пример диагональной матрицы:
d11 0
D 0 d 22
0
0
0
0 .
d33
(1.6)

4.

Единичная матрица. Единичная матрица — это такая диагональная матрица, в
которой все диагональные элементы равны единице. Единичная матрица обычно
обозначается буквой I. Например, единичная матрица размерностью (3˟3) имеет вид:
1 0 0
I 0 1 0 .
0 0 1
(1.7)
В Matlab единичную матрицу (3˟3) можно задать следующим образом:

5.

Транспонированная матрица. Транспонированная матрица получается путем
перемены строк и столбцов. Например,
2 1 1
2 1 2
A 1 1 1 , AТ 1 1 1 ,
2 1 3
1 1 3
(1.8)
где через АТ обозначается матрица, полученная транспонированием А. Транспонирование
обладает следующим свойством:
(AB)T = BTAT.
В Matlab транспонирование обозначается апострофом, т.е. A’ есть матрица, полученная
транспонированием A.

6.

След. Следом квадратной матрица А (обозначается tr A) называется сумма элементов,
стоящих на главной диагонали, т.е.
trA a11 a22
Пример нахождения следа в Matlab:
ann ,
(1.9)

7.

Собственные значения. Собственное
квадратной матрицы – это корни уравнения
значение
λI A 0,
(характеристические
числа)
(1.10)
где символом |‧| обозначен определитель. Иногда также используют обозначение det (‧).
Пример:
Составим характеристическое уравнение. Если исходная матрица
1 6
A
, то
2
6
1 λ 6
del ( λI A)
0
6 λ
2
Раскроем определитель и решим квадратное уравнение:
(1.11)

8.

Раскроем определитель и решим квадратное уравнение:
( 1 λ)(6 λ) 2 ( 6) 0
λ2 5 λ 6 12 0
λ2 5 λ 6 0
D 25 24 1; D 1
5 1
λ1
2;
2
5 1
λ2
3;
2
Таким образом, собственные значения λ1=2, λ2=3.
Выполним определение собственных значений в Matlab.
(1.12)

9.

Собственные векторы. Собственные векторы (Характеристические
квадратной матрицы А – это векторы xi, которые удовлетворяют уравнению
векторы)
λi xi Axi
где λi – собственное значение матрицы А. Собственные значения и собственные векторы
вычисляются с помощью следующей инструкции Matlab:
где D – диагональная матрица, элементами
которой являются собственные значения, а
столбцы матрицы V есть соответствующие
собственные векторы.

10.

Свойства квадратной
следующими свойствами:
матрицы.
Матрица
А
размерности
n
A λi
i 1
n
trA λi
i 1
(1.14)
(n˟n)
обладает

11.

Определители. Если матрицы А и В обе имеют одинаковую размерность (n˟n), то
AB A B
Пример:
(1.15)
a11 a12
Δ A
a11 a22 a12 a21
a21 a22
(1.16)
2 3
Δ A
2 5 3 ( 4) 10 12 2
4 5
Вычислим определитель в Matlab.

12.

Минор. Минор mij вычисляется для aij квадратной матрицы A как определитель
матрицы, получаемый вычеркивание i-й строки и j-го столбца матрицы A из (1.8).
1 1
m31
1 1 2
1 1
(1.17)
Алгебраическое дополнение. Алгебраическое дополнение сij элемента aij квадратной
матрицы А определяется как
i j
сij ( 1) (mij ) 2
(1.18)
Для предыдущего примера
3 1
сij ( 1) ( 2) 2
(1.19)

13.

Присоединенная матрица. Присоединенная матрица к квадратной матрице A
получается при замене каждого элемента aij матрицы А его алгебраическим дополнение с
последующим транспонированием. Присоединенная матрица имеет обозначение Adj A.
Например, для матрицы из (1.8).
c11 c12
Adj ( A) c21 c22
c
31 c32
c13 4 5 1
c23 2 4 0
c33 2 3 1
T
T
(1.20)
Обратная матрица. Для квадратной матрицы А ее обратная матрица, обозначается
А-1, определяется выражением
A 1
Adj ( A)
A
(1.21)
Инструкция Matlab для определения обратной
матрицы имеет вид:
Отметим
матрицы:
два
свойства
( AB) 1 A 1B 1
AA 1 A 1 A I
обратной
(1.22)

14.

Сложение. Чтобы получить сумму двух матриц, A и B, последние должны иметь
одинаковую размерность, и тогда просто необходимо сложить соответствующе элементы
aij и bij. Например,
1 2 2 4 3 6
3 4 6 8 9 12
(1.23)

15.

Умножение на скаляр. Произведение скаляра k и матрицы А – это матрица,
получаемая умножением каждого элемента матрицы А на скаляр k.
a11
B kA k
a21
a12 ka11
a22 ka21
ka12
(1.24)
ka22

16.

Умножение векторов. Умножение вектора размерностью (1˟n) на вектор (n˟1)
определяется как
x1
x2
y1
y2
xn
x1 y1 x2 y2
yn
xn yn
Заметим, что при умножении векторов получается скаляр.
(1.25)

17.

Умножение матриц. Матриц А размерностью (m˟p) может быть умножена только на
матрицу B размерности (p˟n), т.е. число столбцов матрицы А должно равняться числу
строк матрицы B. Тогда произведение матриц будет иметь размерность (m˟n). Если
С AB
(1.26)
то ij-й элемент матрицы C образуется как
векторное произведение i-й строки матрицы A на j-й
столбец матрицы B.
В качестве примера найдем
рассмотренных выше матриц А и А-1.
произведение
1 1 1 0 0
2 1 1 2
0 1 0 L
AA 1 1 1 1
2.5
2
3
/
2
2 1 3 0.5 0 0.5 0 0 1
(1.27)

18.

Дифференцирование. Производная матрицы получается путем дифференцирования
каждого элемента этой матрицы. Пусть, например,
x1
x .
x2
Тогда
dx1
dx dt
.
dt dx2
dt
(1.28)
Интегрирование. Интеграл от матрицы получается путем интегрирования каждого
элемента этой матрицы.
Например, для вектора x
x1dt
.
xdt
x dt
2
(1.29)

19.

Полезное выражение для определителя. Дана блочная матрица
D E
H
F
G
в которой D, E, F и G – матрицы размерностью (n˟n). Тогда H имеет размерность
(2n˟2n), а ее определитель вычисляется как
H G D EG 1F D G FD 1E
при условии, что указанные обратные матрицы существуют.
(1.30)

20.

Комплексные числа
Комплексным числом z называется выражение вида z x iy
, где x, y –действительные числа, i − так называемая мнимая
единица, i2=-1 .
Числа x, y называются соответственно действующей и
мнимой частью комплексного числа z и обозначаются
x Re z y lmz
Комплексное число z x iy
изображено точкой М плоскости с координатами x,y или ее радиус вектором ОМ
(рисунок). Длина вектора ОМ называется модулем комплексной переменной числа z и
обозначается z или r:
2
2
z r OM x y
На ряду с алгебраической формой z x iy комплексного числа рассмотрим еще две формы записи.
можно
x r cos y r sin , то комплексное число z x iy
Можно записать в тригонометрической форме z r (cos i sin )
i
Введя функциюe cos i sin , комплексное число можно записать в показательной форме:
z r ei
Итак, имеем три формы записи комплексного числа.
z x iy r (cos i sin ) r ei

21.

Преобразование Лапласа.
.
По определению преобразование Лапласа f (t ) функции времени равно
F ( s ) L[ f (t )] f (t )e st dt (2.1)
0
где L есть символ преобразования Лапласа. Заметим, что при интегрировании
переменная t (время) исчезает, и преобразование Лапласа представляет собой функцию
комплексной переменной s.
Обратное преобразование Лапласа определяется выражением
j
1
f (t ) L F (s)
F (s) est ds
2 j j
1
(2.2)
где L 1 есть символ обратного преобразования Лапласа, а j 1
Величина σ в выражении 2.2 определяется особенностями функции F (s)
Для нахождения обратного преобразования Лапласа выражение 2.2 используется редко.
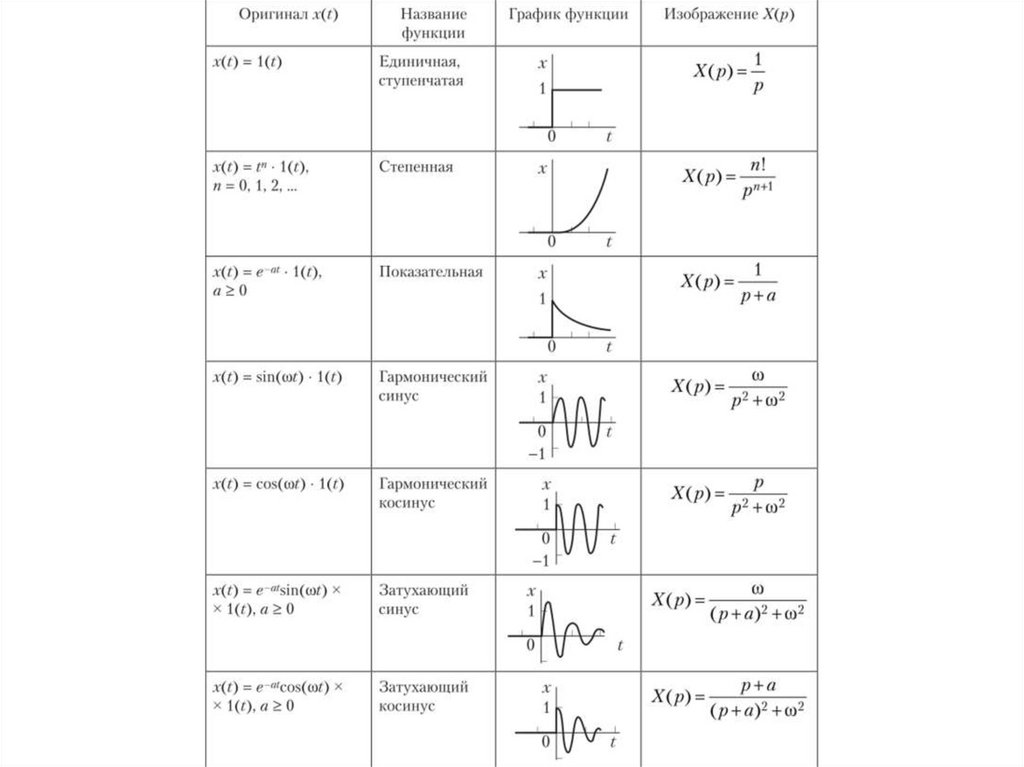
Вместо этого с помощью 2.1 преобразование Лапласа для наиболее распространенных
функций времени сведены в таблицу, по которой в случае необходимости устанавливается
соответствие между оригиналом и функцией f (t ) и ее изображение по Лапласу F (s)
e (s a)t
1
1
at
st
(s a)t
F (s) e e dt e
dt
0
;Re(s a) 0
s
a
s
a
s
a
0
0
0
где Re обозначена действительная часть выражения.
(2.3)

22.

23.

Из определения преобразования Лапласа следует, что
если k = const, то
L[kf (t )] kL[ f (t )] kF (s)
(2.4)
и
L[ f1 (t ) f 2 (t )] L[ f1 (t )] L[ f 2 (t )] F1 ( s ) F2 ( s ) (2.5)
Использование этих двух
расширяет применение таблицы 1.
соотношений
значительно

24.

Пример 2.1.
Найти преобразование Лапласа для функции
f (t ) 5 u(t ) 3 e 2t
Кроме того, чтобы упростить обозначения, определим единичную ступенчатую функцию
u(t ) следующим образом:
0, t 0,
u(t )
1, t 0.
(2.6)
L[5u(t )] 5L[u (t )]
5
s
L[3e 2t ] 3 L[e 2t ]
3
s 2
Далее, согласно 2.5
F ( s) L[5u (t ) 3e 2t ]
Этому выражению можно придать иную форму
F ( s)
5
3
s s 2
5
3
8s 10
s s 2 s( s 2)

25.

Пример 2.2
Найдем обратное преобразование Лапласа для функции
F ( s)
5
5
s 2 3s 2 ( s 1)( s 2)
Сначала разложим на простые дроби:
F ( s)
5
k1
k2
( s 1)( s 2) ( s 1) ( s 2)
Вычислим коэффициенты k1 и k2
5
s 1 5
( s 2)
5
k2 ( s 2) F ( s) s 2
s 2 5
( s 1)
Тогда разложение на простые дроби примет вид:
k1 ( s 1) F ( s) s 1
5
5
5
( s 1)( s 2) s 1 s 2
Это разложение легко проверить путем приведения к общему знаменателю двух
слагаемых в правой части. В результате обратного преобразования Лапласа для F(s) имеет
вид:
L 1[ F (s)] (5e t 2e 2t )u(t )

26.

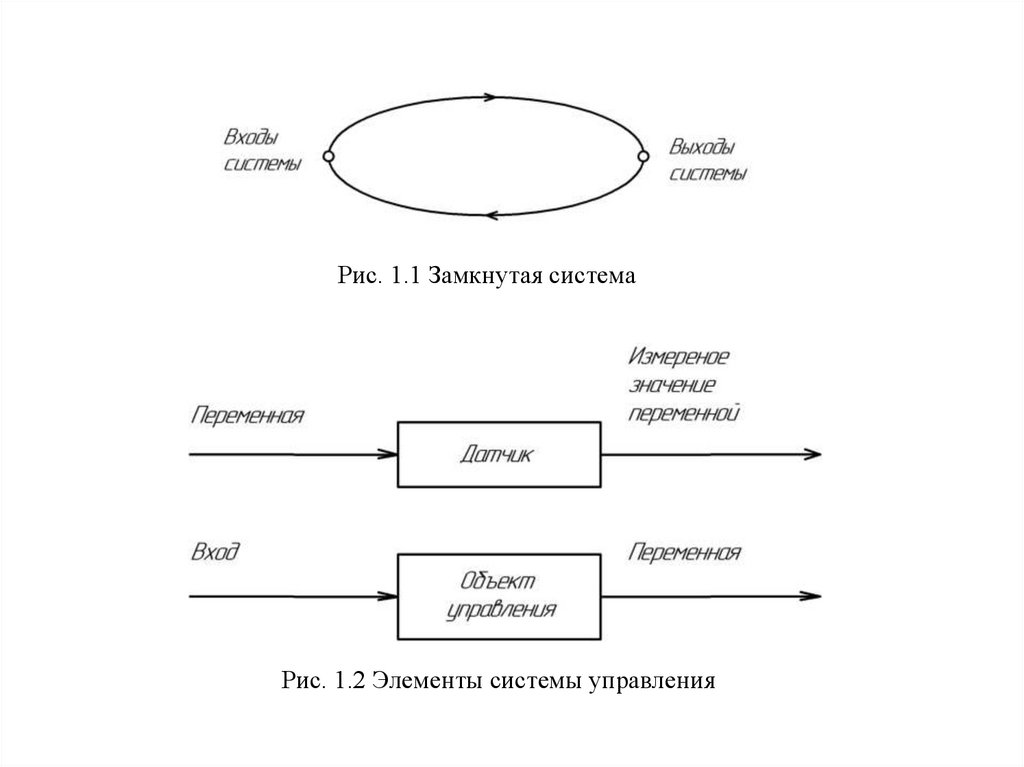
Рис. 1.1 Замкнутая система
Рис. 1.2 Элементы системы управления

27.

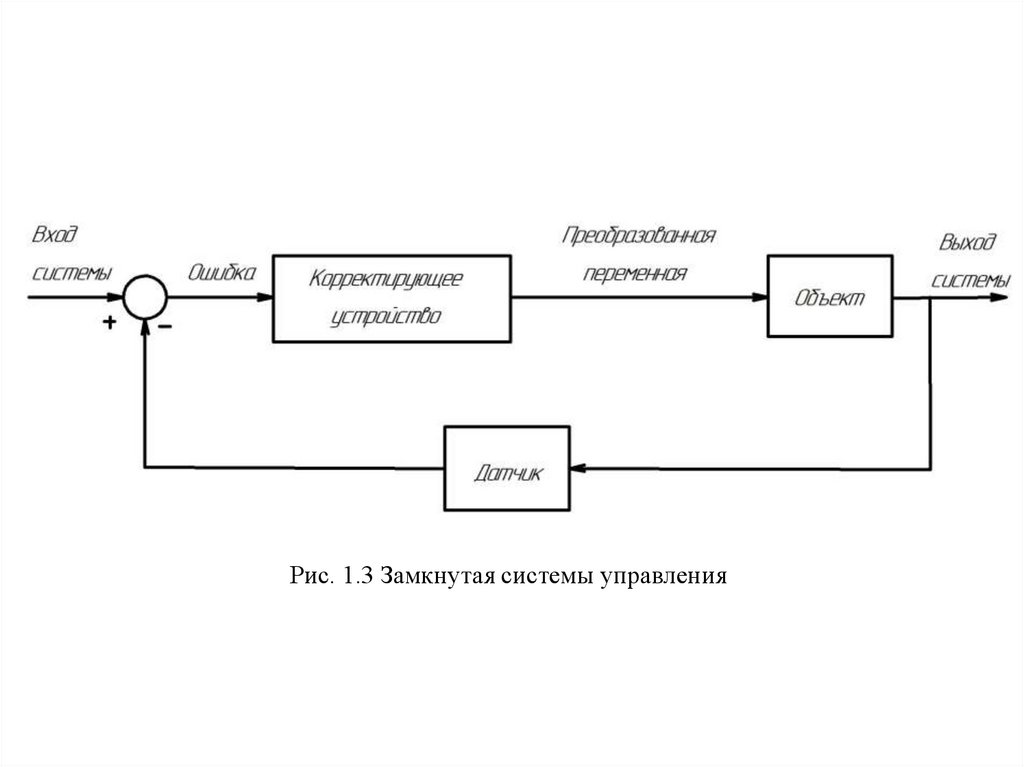
Рис. 1.3 Замкнутая системы управления

28.

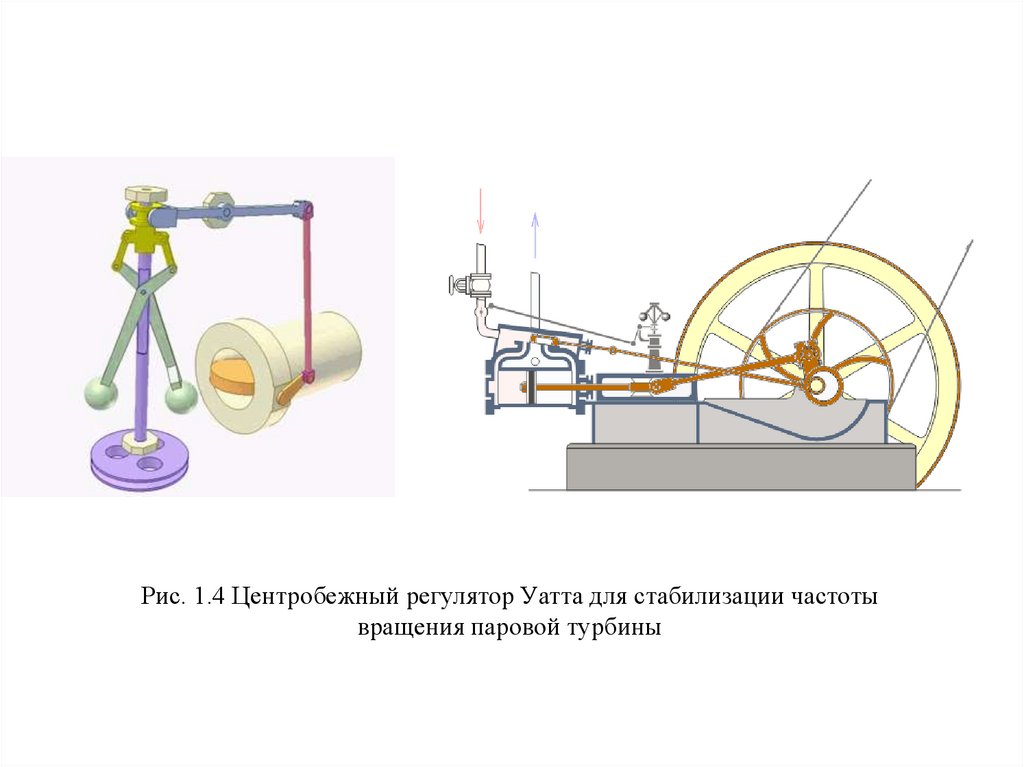
Рис. 1.4 Центробежный регулятор Уатта для стабилизации частоты
вращения паровой турбины

29.

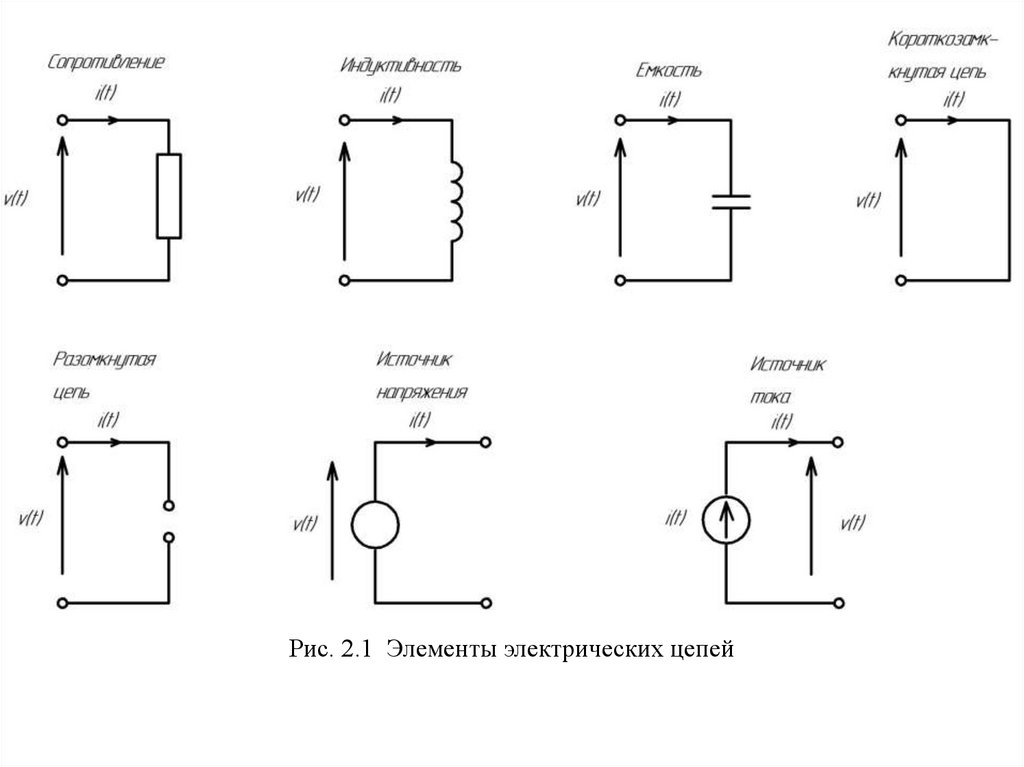
Рис. 2.1 Элементы электрических цепей

30.

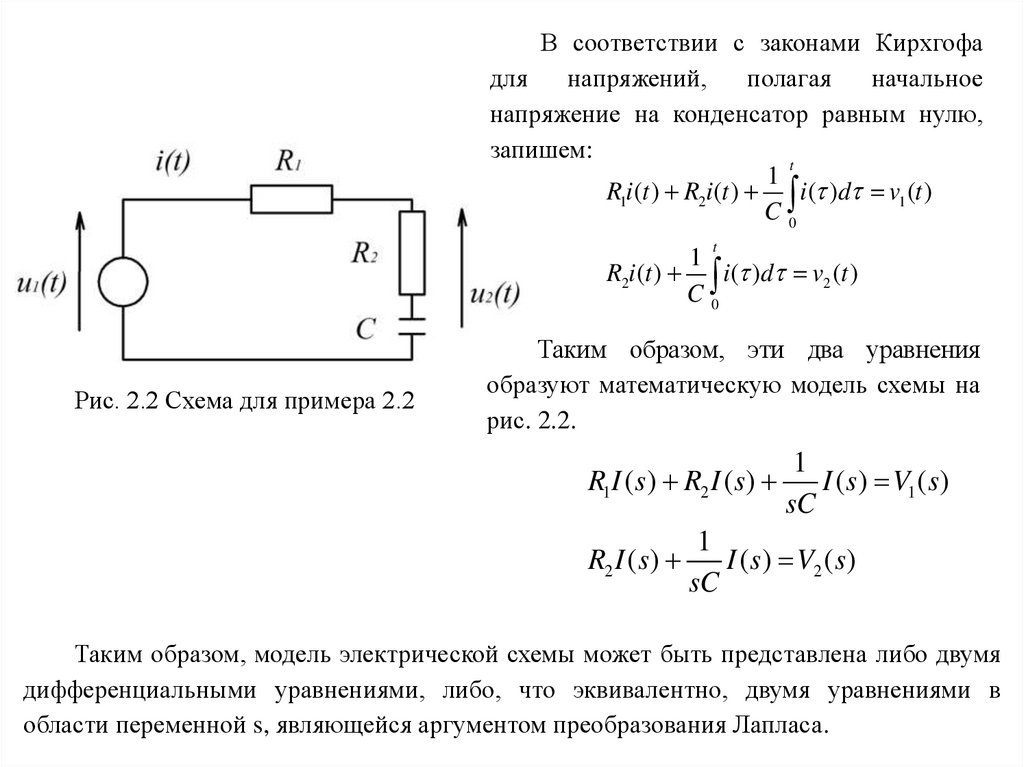
В соответствии с законами Кирхгофа
для
напряжений,
полагая
начальное
напряжение на конденсатор равным нулю,
запишем:
t
1
R1i (t ) R2i (t ) i ( )d v1 (t )
C0
t
1
R2i (t ) i ( )d v2 (t )
C0
Рис. 2.2 Схема для примера 2.2
Таким образом, эти два уравнения
образуют математическую модель схемы на
рис. 2.2.
1
R1I (s) R2 I (s)
I (s) V1 (s)
sC
1
R2 I ( s)
I ( s) V2 ( s)
sC
Таким образом, модель электрической схемы может быть представлена либо двумя
дифференциальными уравнениями, либо, что эквивалентно, двумя уравнениями в
области переменной s, являющейся аргументом преобразования Лапласа.

31.

Рассмотрим теперь систему с входом e(t) и выходом с(t). Если C(s) – изображение по
Лапласу переменной с(t), а Е(s) – изображение по Лапласу переменной e(t), то
передаточная функция системы G(s) по определению равна
C ( s)
G( s)
E ( s)
Выразим из первого уравнения I(s):
V1 ( s)
I ( s)
R1 R2
1
sC
Подставим во второе уравнение ранее выраженное для I(s):
V2 ( s )
R2
1
sC
1
( R1 R2 )
sC
V1 ( s )
Отсюда легко получить выражение для передаточной функции G(s):
G( s)
V2 ( s)
R2 sC 1
V1 ( s) ( R1 R2 ) sC 1
Таким образом, для схемы рис. 2.2 одинаковую силу имеют как дифференциальные
уравнения, полученные в примере 2.2, так и передаточная функция, найденная в данном
примере. Очевидно, всегда легко можно перейти о одной формы уравнений к другой.

32.

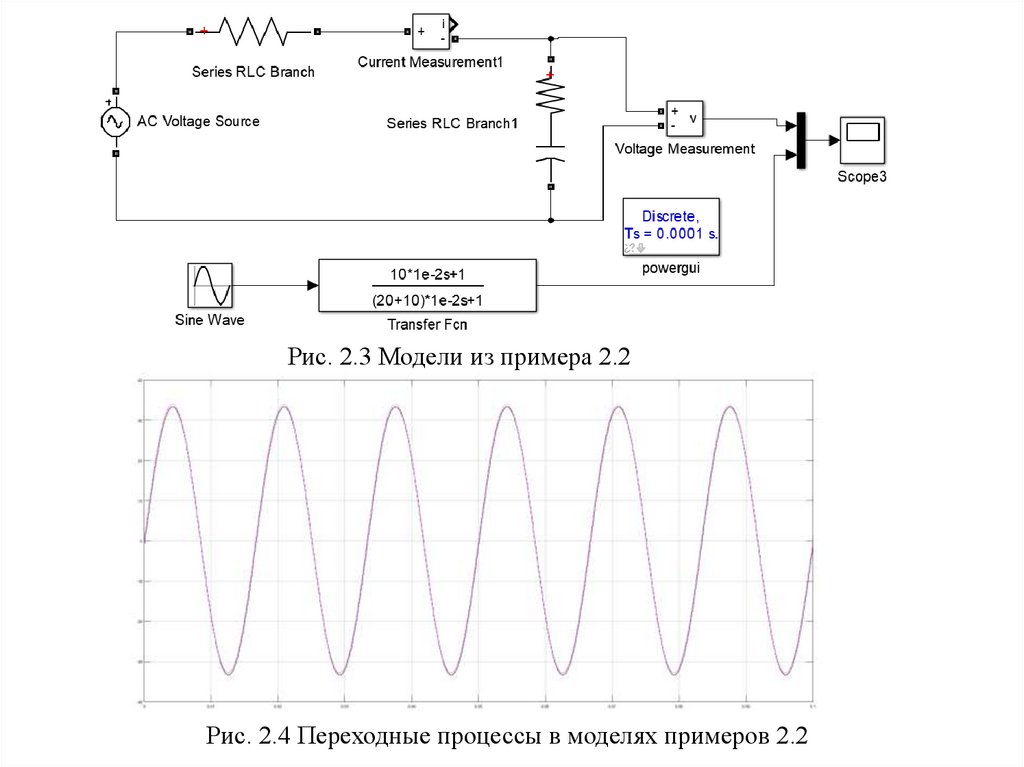
Рис. 2.3 Модели из примера 2.2
Рис. 2.4 Переходные процессы в моделях примеров 2.2

33.

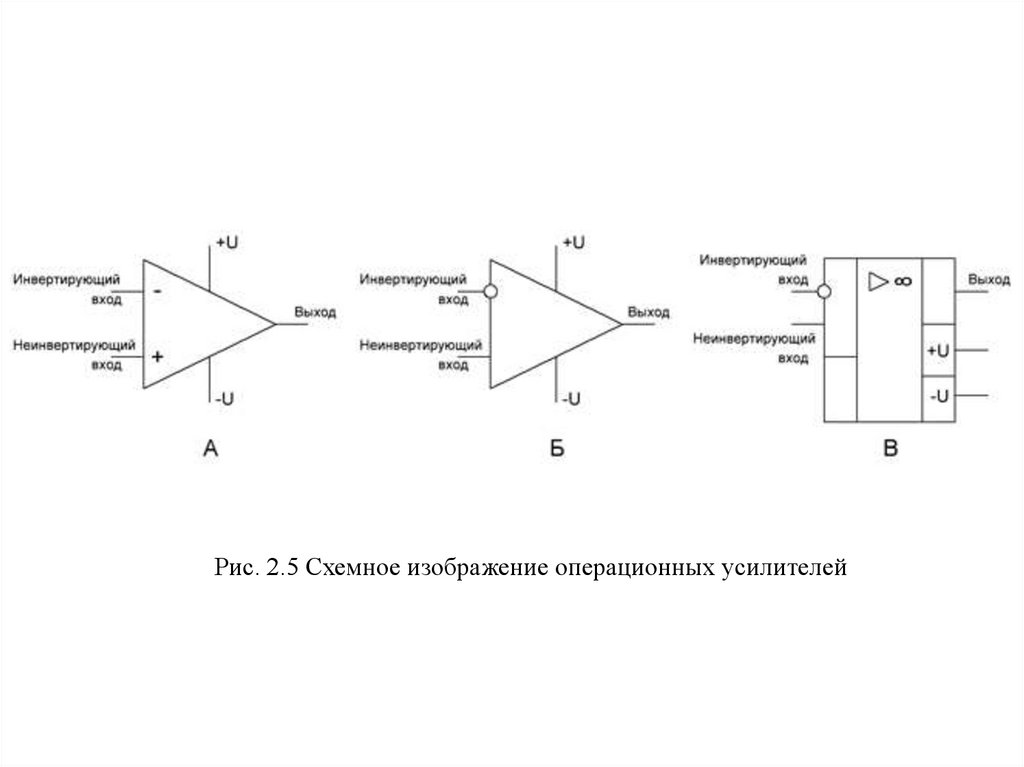
Рис. 2.5 Схемное изображение операционных усилителей

34.

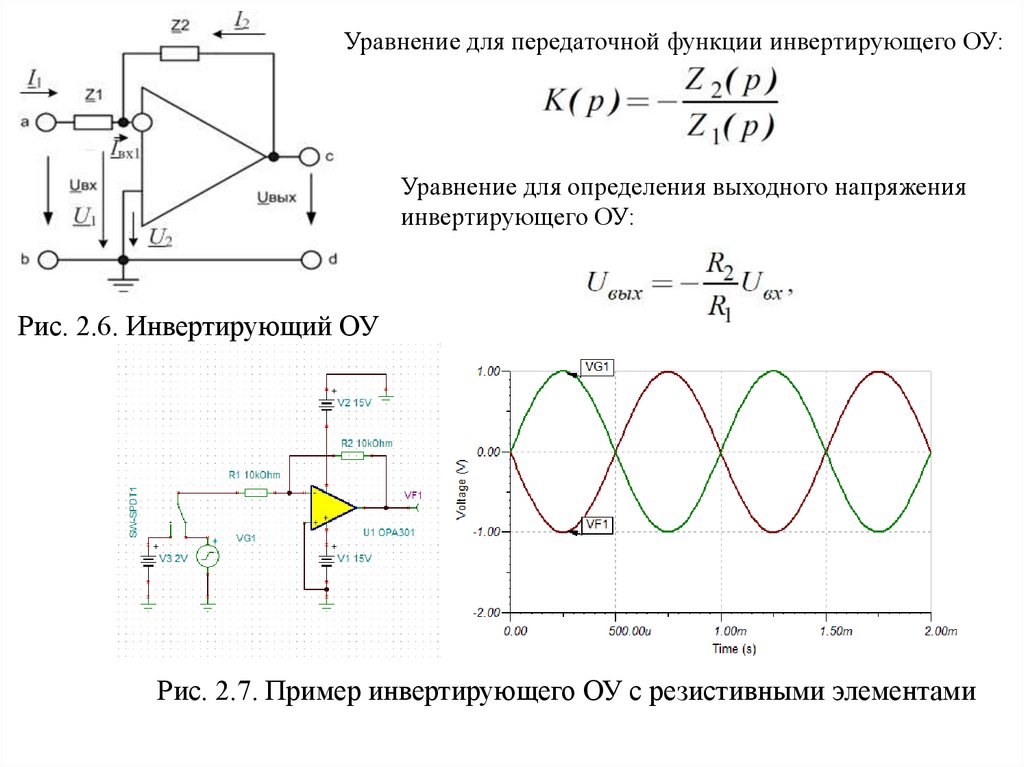
Уравнение для передаточной функции инвертирующего ОУ:
Уравнение для определения выходного напряжения
инвертирующего ОУ:
Рис. 2.6. Инвертирующий ОУ
Рис. 2.7. Пример инвертирующего ОУ с резистивными элементами

35.

Уравнение для передаточной функции неинвертирующего ОУ:
Уравнение для определения выходного напряжения
неинвертирующего ОУ:
Рис. 2.8. Неинвертирующий ОУ
Рис. 2.9. Пример неинвертирующего ОУ с резистивными элементами

36.

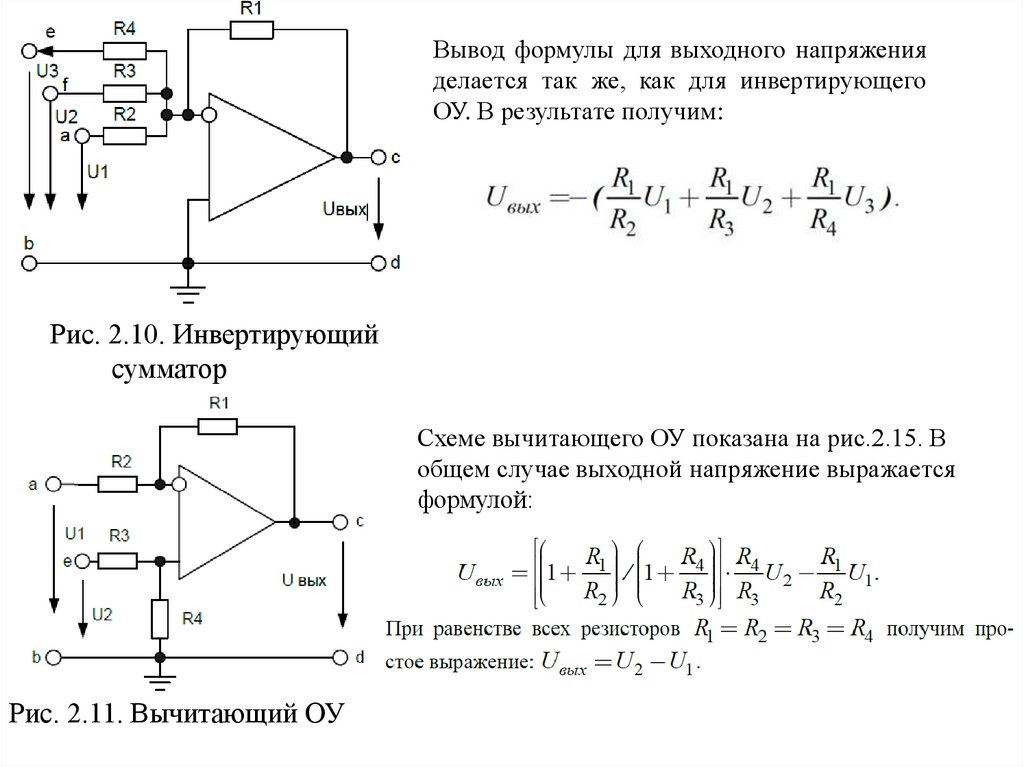
Вывод формулы для выходного напряжения
делается так же, как для инвертирующего
ОУ. В результате получим:
Рис. 2.10. Инвертирующий
сумматор
Схеме вычитающего ОУ показана на рис.2.15. В
общем случае выходной напряжение выражается
формулой:
Рис. 2.11. Вычитающий ОУ

37.

Схема дифференцирующего звена показана на рис.2.17.
Выведем формулу для выходного напряжения. По
первому закону Кирхгофа:
Входной ток
Напряжение между входами (виртуальный нуль):
Рис. 2.12. Дифференцирующее
звено
Рис. 2.13. Пример применения дифференцирующего звена

38.

Рис. 2.14.
Интегрирующее
звено
Модель демонстрирует работу интегратора при действии на
входе прямоугольных импульсов с амплитудой 1В и периодом
20мс от генератора VG1.
На выходе мы получаем треугольный сигнал с минимальным
напряжением:
Моделирование подтверждает
расчет. Если в схеме резистор
R1 заменить емкостью С,
получим
суммирующий
инвертирующий интегратор.
Рис. 2.15. Пример применения интегрирующего звена

39.

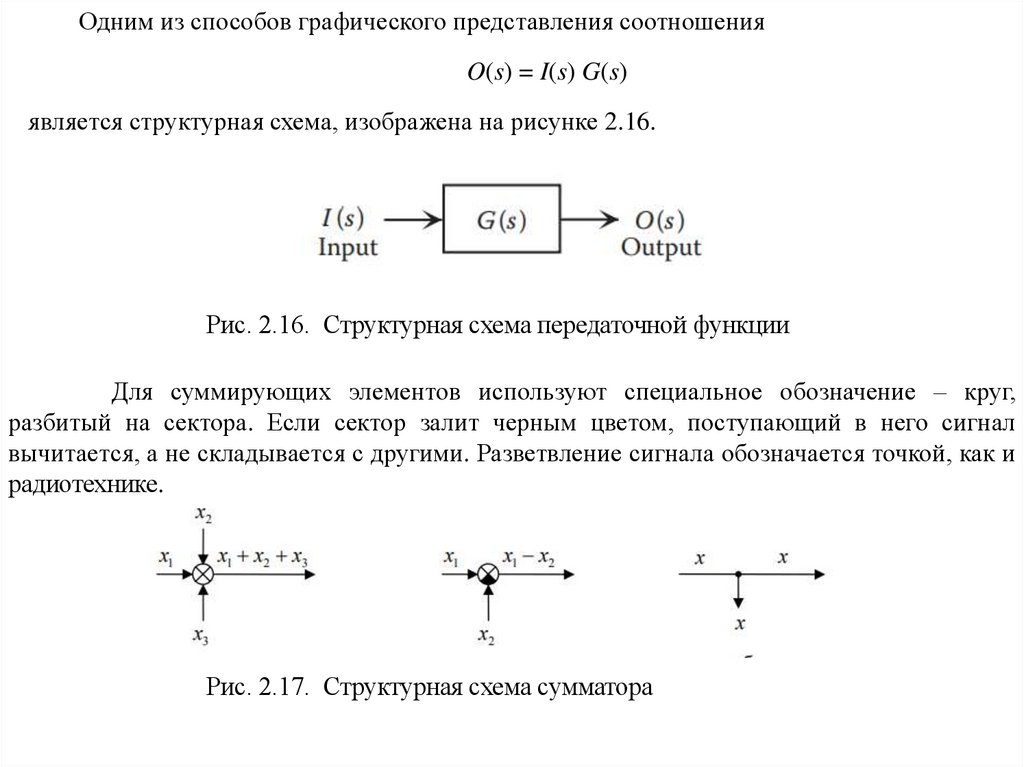
Одним из способов графического представления соотношения
O(s) = I(s) G(s)
является структурная схема, изображена на рисунке 2.16.
Рис. 2.16. Структурная схема передаточной функции
Для суммирующих элементов используют специальное обозначение – круг,
разбитый на сектора. Если сектор залит черным цветом, поступающий в него сигнал
вычитается, а не складывается с другими. Разветвление сигнала обозначается точкой, как и
радиотехнике.
Рис. 2.17. Структурная схема сумматора

40.

Передаточная функция последовательного соединения:
Рис. 2.18. Последовательное соединение двух передаточных функций
Выход второго блока Y(s) = G2(s)X(s). Но поскольку X(s) является выходом первого блока,
и определяется как X(s) = G1(s) U(s), имеем
Следовательно,
Таким образом, последовательная конфигурация на рис. 2.18 может быть заменена одним
блоком G1(s)G2(s) , с общим входом U(s) и выходом Y(s)
Рис. 2.19. Передаточная функция двух последовательно соединённых
передаточных функций

41.

Рассмотрим два последовательно соединённых блока с передаточными функциями
Передаточная функция эквивалентного блока определяется в MATLAB следующим
образом.
Конечный результат соответствует полученному аналитически

42.

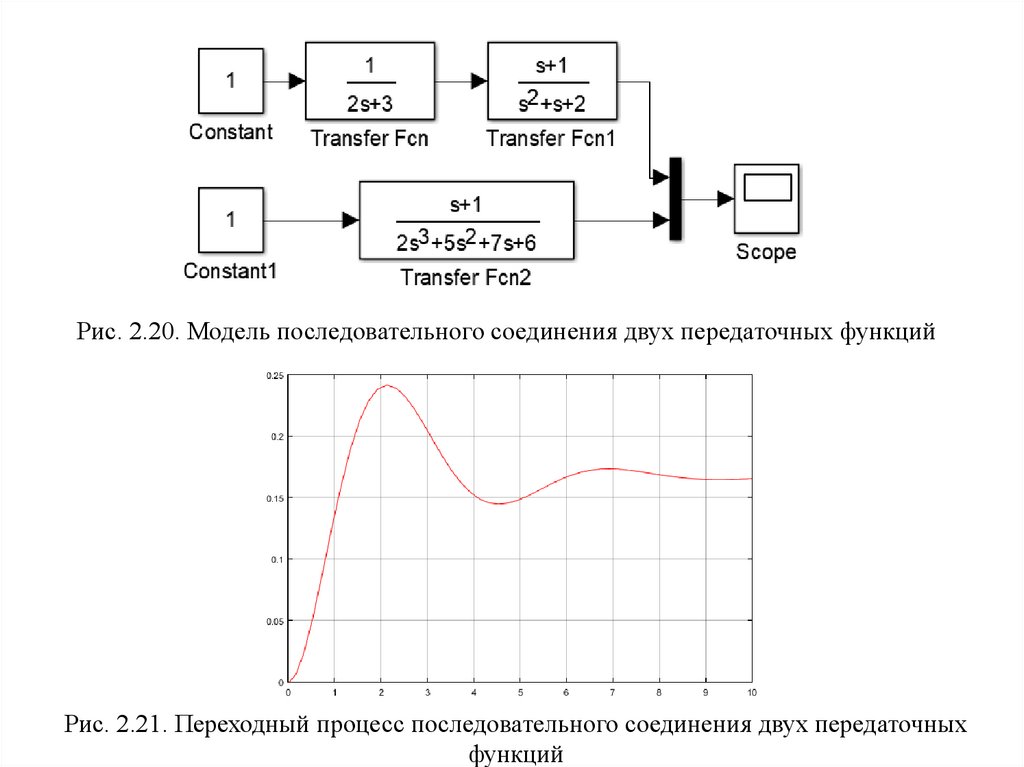
Рис. 2.20. Модель последовательного соединения двух передаточных функций
Рис. 2.21. Переходный процесс последовательного соединения двух передаточных
функций

43.

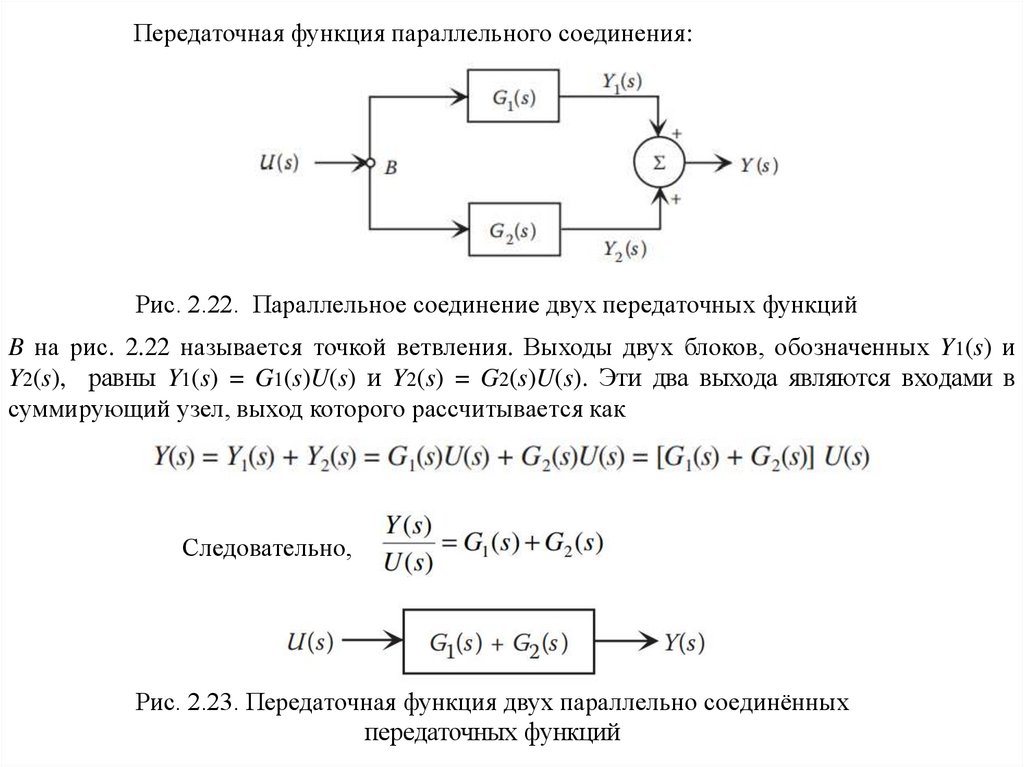
Передаточная функция параллельного соединения:
Рис. 2.22. Параллельное соединение двух передаточных функций
B на рис. 2.22 называется точкой ветвления. Выходы двух блоков, обозначенных Y1(s) и
Y2(s), равны Y1(s) = G1(s)U(s) и Y2(s) = G2(s)U(s). Эти два выхода являются входами в
суммирующий узел, выход которого рассчитывается как
Следовательно,
Рис. 2.23. Передаточная функция двух параллельно соединённых
передаточных функций

44.

Рассмотрим два параллельно соединённых блока с передаточными функциями
Передаточная функция для эквивалентного блока находится в MATLAB следующим
образом:

45.

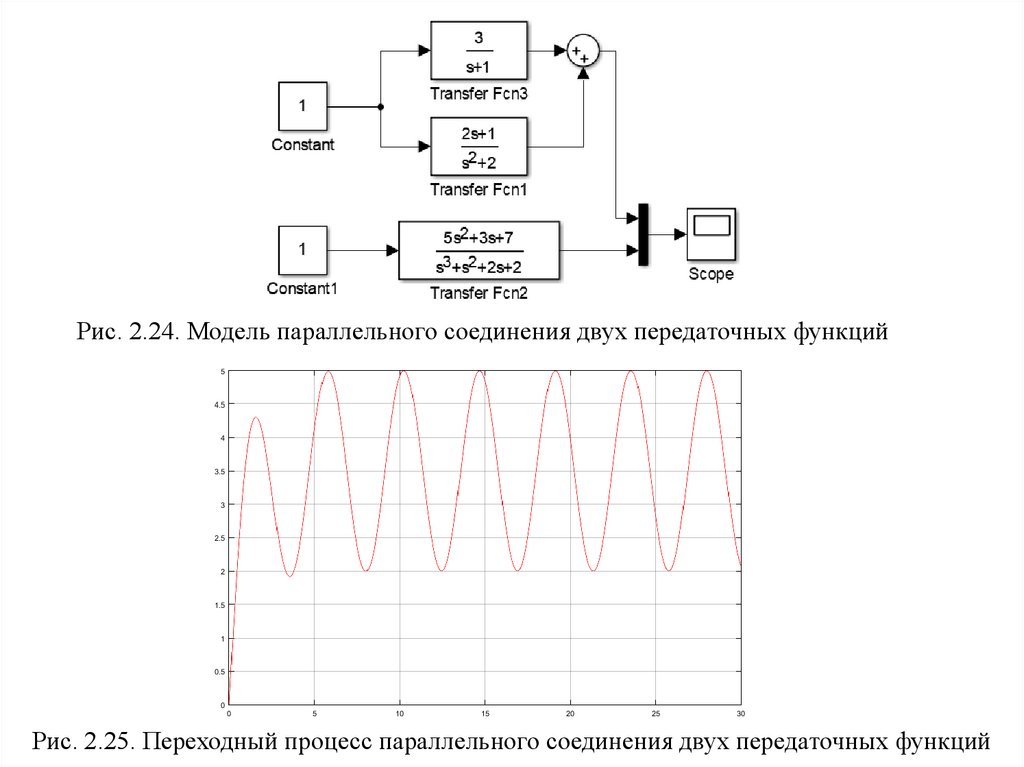
Рис. 2.24. Модель параллельного соединения двух передаточных функций
Рис. 2.25. Переходный процесс параллельного соединения двух передаточных функций

46.

Рассмотрим сигнал u(t), интегрированный от начального времени 0 до текущего времени
t, чтобы произвести
Это уравнение после прямого преобразования Лапласа имеет вид:
Таким образом, интегратор представлен одним блоком с передаточной функцией 1/s
как на рис. 2.26.
Рис. 2.26. Переходный процесс параллельного соединения двух передаточных функций

47.

Замкнутые системы
На рис. 2.27 показана система с обратной связью. Вход U(s). Выход Y(s) возвращается
через элемент обратной связи H(s), выход C(s) которого сравнивается с входом U(s) на
суммирующем переходе. Разница E(s) = U(s) − C(s) известна как сигнал ошибки. Из-за
отрицательного знака, связанного с C(s) в суммирующем переходе, конфигурация на рис.
2.27 известна как система отрицательной обратной связи.
В замкнутой системе на рис. 2.27 есть две важные передаточные функции:
упреждающая передаточная функция
передаточная функция без обратной связи
Это последнее соотношение можно проверить, заметив, что Y(s) = E(s)G(s) является
входом элемента обратной связи. H(s), таким образом, C(s) = H(s) Y(s) = H(s) E(s)G(s).
Рис. 2.27. Схема системы c отрицательной обратной связью

48.

Передаточная функция замкнутой системы
Передаточная функция замкнутой системы (ПФЗС) обеспечивает прямую связь между
входом U(s) и выход Y(s) и определяется следующим образом (см. рис. 2.27 ):
Преобразуя приведенным выше уравнением, находим
ПФЗС c отрицательной обратной связью формируется как:
Аналогично, в случае положительной обратной связи:

49.

Рассмотрим систему отрицательной обратной связи, показанную на рис. 2.27, и
предположим, что
Тогда,
Передаточная функция для ПФЗС находится в MATLAB следующим образом:

50.

Методы сокращения блок-диаграмм
Перемещение точки ветвления
Рассмотрим точку ветвления B на рис. 2.28а, расположенную слева от блока G(s).
Точка разветвления можно переместить на правую сторону блока G(s), как показано на рис.
2.28b. Найдем сигналы Y1(s) и Y2(s) для передачи одной и той же информации до и после
перемещения B. Очевидно, что Y1(s) = G(s)U(s) в обоих случаях. Тогда Y2(s) = U(s) до
перемещения B, и Y2(s) = [1/G(s)] G(s)U(s)= U(s) после перемещения.
Рис. 2.28. Перемещение точки ветвления

51.

Перемещение сумматора
Рассмотрим сумматор в схеме, показанной на рис. 2.29а. Сумматор можно
переместить на левую сторону блока G1(s), как показано на рис. 2.29b. Обязательным
является то, что сигнал Y(s) должен нести одну и ту же информацию до и после
суммирующего соединения. По рисунку 2.29а видно, что Y(s) = G1(s)U1(s) + G2(s)U2(s).
Тогда для на рис. 4.15b мы имеем:
Рис. 2.29. Перемещение сумматора

52.

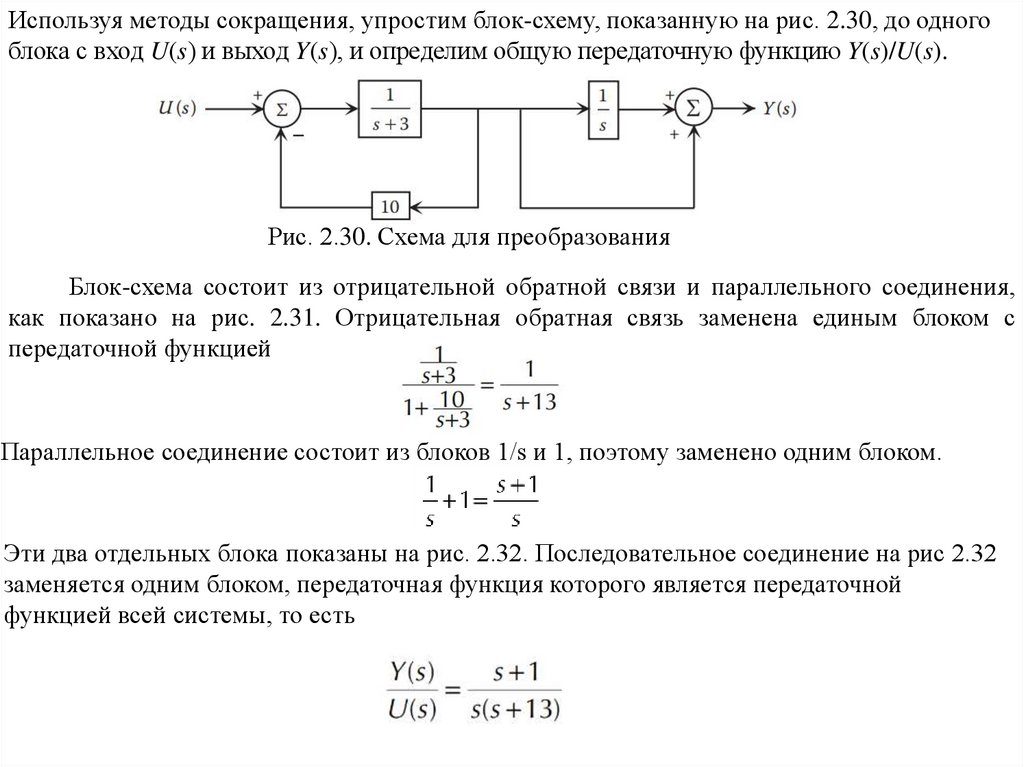
Используя методы сокращения, упростим блок-схему, показанную на рис. 2.30, до одного
блока с вход U(s) и выход Y(s), и определим общую передаточную функцию Y(s)/U(s).
Рис. 2.30. Схема для преобразования
Блок-схема состоит из отрицательной обратной связи и параллельного соединения,
как показано на рис. 2.31. Отрицательная обратная связь заменена единым блоком с
передаточной функцией
Параллельное соединение состоит из блоков 1/s и 1, поэтому заменено одним блоком.
Эти два отдельных блока показаны на рис. 2.32. Последовательное соединение на рис 2.32
заменяется одним блоком, передаточная функция которого является передаточной
функцией всей системы, то есть

53.

Рис. 2.31. Блок-схема отрицательной обратной связи и параллельного соединения
Рис. 2.32. Последовательное соединение частей передаточной функции
Рис. 2.33. Передаточная функция всей системы одним блоком

54.

Рис. 2.34. Модель эквивалентной передаточной функции
Рис. 2.35. Переходный процесс эквивалентной передаточной функции

55.

Модели механических систем
Элементы Массы
Основные переменные, используемые для описания динамическое поведение
поступательной механической системы – вектор ускорения a, вектор скорости v и вектор
положения r.
Рис. 3.1. Масса m, движущаяся со скоростью v.
Они связаны производными по времени:
который также может быть представлен в простой точечной форме:
Предположим, что движение массы на рис. 3.1 происходит под влиянием
приложенной извне силы и только в одном направлении. Согласно ньютоновской механике,
в результате сила f, действующая на массу, равна скорости изменения импульса во времени.
Для постоянной массы второй закон Ньютона выражается как

56.

Элементы массы накапливают механическую энергию. Энергия, запасенная в массе
если она находится в движение, называется кинетической. Кинетическая энергия
выражается как
что означает, что масса накапливает кинетическую энергию по мере увеличения ее
скорости и высвобождает кинетическую энергии по мере уменьшения его скорости. Если
масса имеет вертикальное перемещение относительно исходного положения, энергия,
запасенная в массе, является потенциальной энергией, определяемой выражением
где g — ускорение свободного падения (9,81 м/с2), а h — высота, измеренная от исходного
положения или относительно центра масс. Нижний индекс g используется для обозначения
того, что потенциал энергия связана с гравитацией.
Для вращательных механических систем основными переменными, используемыми для
описания динамики системы, являются вектор углового ускорения α, вектор угловой
скорости ω и вектор углового положения θ. Направление углового вектора можно
определить с помощью правила правой руки, как показано на рис. 3.2. Направление
вращения повторяет изгиб четырех пальцев, а вектор вращения совпадает с направлением
большого пальца. В этой главе мы рассмотрим твердые тела, которые вращаться только по
одной оси. Тогда в скалярной форме имеем:

57.

Рис. 3.2. Правило правой руки
Рис. 3.3. Диск, вращающийся
вокруг оси, проходящей через
неподвижную точку О.
На рис. 3.3 показан диск, вращающийся вокруг оси,
проходящей через неподвижную точку O. Соотношение
между крутящим моментом τ относительно неподвижной
точки O и угловое ускорение α диска равны:
где IO - момент инерции массы тела относительно
неподвижной точки O, и используемые общепринятые
единицы
кг*м^2. Подобно поступательной массе,
вращающаяся масса может накапливать кинетическую
потенциальную энергии. Кинетическая энергия массы,
вращающейся вокруг неподвижной точки O, выражается
как:

58.

Пружинные элементы
На рис. 3.4а показан элемент поступательной пружины, который закреплен на одном
конце и подвергается воздействию растягивающие (или сжимающей) силы f на другом
конце. Пружина имеет длину x0 в свободном состоянии, и прогиб x, вызванный силой f.
Предположим, что пружина не имеет массы или масса пренебрежимо мала. Для линейной
пружины закон Гука гласит, что
Рис. 3.4. Поступательный пружинный элемент с (а) одним фиксированным концом и (б)
двумя свободными концами.
где k — жесткость пружины в Н/м. Если пружина соединена с массой, то согласно
третьему закону Ньютона сила, действующая на массу со стороны пружины, имеет ту же
величину, что и f, но противоположные по направлению. Когда два конца пружины
смещены на x1 и x2, как показано на рисунке 3.4б, силы на двух концах равны по величине,
но противоположны по направлению. Если x2 > x1 > 0, то пружина растягивается, а сила,
приложенная к пружине, равна

59.

Когда пружина растягивается или сжимается, потенциальная энергия накапливается в
пружине и равняется:
где индекс e означает, что потенциальная энергия связана с упругими элементами.
Рис. 3.5. Пружинный элемент кручения с (а) одним закрепленным концом и (б) двумя
свободными концами.
Для торсионной пружины, показанной на рис. 3.5а, имеем
где τ — приложенный крутящий момент, K — жесткость пружины на кручение в Н·м/рад,
θ — угловая деформация пружины. На рис. 3.5b показана торсионная пружина
скручиваемая с обоих концов. Предположим, что θ1 и θ2 — угловые смещения концов,
соответствующие приложенный крутящий момент. Если θ2 > θ1 > 0, то
и пружина закручена против часовой стрелки, если смотреть с правой стороны.
Потенциальная энергия, запасенная в пружинном элементе кручения, выражается как

60.

Демпферные элементы
Пружинный элемент создает реактивную силу, которая зависит от относительного
смещения двух концы пружин. Напротив, сила, которая зависит от относительной скорости
между двумя телами, моделируется демпферным элементом. На рис. 3.6 показано
скольжение массы по неподвижной горизонтальной поверхности, где две поверхности
разделены жидкостной пленкой. На массу действует сила трения между двумя
поверхностями, а трение, возникающее в жидкости, называется вязким трением.
Направление демпфирующей силы противоположно направлению движения и ее величина
зависит от характера течения жидкости между двумя поверхностями. Точно рассчитать
демпфирующую силу сложно, таким образом, для моделирования динамических систем
мы используем линейную зависимость:
где символ b используется для обозначения коэффициента вязкого демпфирования в
единицах Н·с/м. Демпфирующая сила, действующая на массу на рис. 3.6, направлена
влево.
Рис. 3.6. Масса, скользящая по неподвижной поверхности.

61.

Вязкое трение можно моделировать с помощью вязкого демпфера (или демпфера).
Символ на рисунке 3.7а представляет собой изображение вязкого демпфера, похожего на
поршень, движущийся через заполненную жидкостью цилиндр, как показано на рисунке
3.7b. В поршне есть небольшие отверстия, через которые протекает жидкость по мере
движения частей относительно друг друга. Если v2 > v1 > 0, то правый конец заслонки
перемещается справа по отношению к левому концу. Сила, приложенная к правому концу,
зависит от относительной скорости vотн = v2 − v1. Сила имеет величину и указывает
вправо:
Рис. 3.7. Масса, скользящая по неподвижной поверхности.

62.

Предположим, что демпфер не имеет массы или имеет пренебрежимо малую массу.
Тогда силы на двух концах демпфера равны по величине, но противоположны по
направлению. Для торсионного гасителя, показанного на рис. 3.8а, линейная зависимость
между внешним приложенный крутящий момент, а угловая скорость определяется
выражением
Рис. 3.8. Вращающийся вязкий демпфер с (а) одним закрепленным концом и (б) двумя
свободными концами.
где B — коэффициент вязкостного демпфирования при вращении в единицах Н·м·с/рад.
Символ на рис. 3.8b представлен вращательный вязкий демпфер, который можно
использовать для моделирования вязкого трения между двумя вращающимися
поверхностями, разделенными пленкой жидкости. Если ω2 > ω1 > 0, величина
приложенный крутящий момент

63.

Эквивалентное преобразование механических моделей
Рассмотрим систему из двух пружин k1 и k2, соединенных параллельно, как показано на
рис. 3.9. Докажем, что система эквивалентна одинарной пружине, жесткость которой равна
Из-за параллельного соединения нижние концы пружин крепятся к одному и тому же
неподвижному тело, а их верхние концы также прикреплены к общему телу. Это означает,
что обе пружины имеют тот же прогиб х. Предположим, что силы, приложенные к двум
пружинам, равны f1 и f2 соответственно. Поскольку система находится в статическом
равновесии, общая сила определяется выражением
Представим ее с эквивалентной системой,
получаем эквивалентную жесткость пружины
Результат можно распространить на n
пружин.
Для системы из n
параллельных пружин эквивалент
жесткость пружины keq равна сумме
всех
отдельных
коэффициентов
жесткости пружины ki:
Рис. 3.9. Эквивалентное соединение
двух параллельных пружин.

64.

Рассмотрим систему из двух последовательно соединенных пружин k1 и k2, как показано
на рис. 3.10. Докажем, что эквивалентная пружинная жесткость системы
Поскольку обе пружины находятся в статическом равновесии, на них
действует одинаковая сила f. Предполагается что две пружины
деформируются на x1 и x2 соответственно. Полная деформация
системы равна:
Для эквивалентной системы деформация равна:
Таким образом,
или
Результат также можно распространить
на n пружин. Для системы из n
последовательно соединенных пружин
обратная эквивалентной жесткости
пружины keq равно сумме всех
обратных величин индивидуальной
коэффициенты жесткости пружины ki:
Рис. 3.10. Эквивалентное соединение
двух последовательных пружин.

65.

Эквивалентная жесткость консольной балки
Соотношение силы и отклонения консольной балки можно найти в литературе по
механике. Это соотношение равно:
где x — прогиб на свободном конце балки, f — сила, приложенная к свободному концу
балки, E — модуль упругости материала балки, IA — момент инерции площади
относительно продольная ось балки. Для балки прямоугольного сечения шириной b и
толщина h, площадь момента инерции равна
Таким образом, соотношение сила-прогиб сводится к
Для эквивалентной системы
соотношение
сила-прогиб
имеет вид:
Таким образом, эквивалентная
жесткость пружины равна
Рис. 3.11. Изгиб балки под действием поперечной силы.

66.

Степени свободы
Число степеней свободы динамической системы – это число независимых
геометрических параметров однозначно определяющих положение всех масс системы.
На рис. 3.12а показана поступательная механическая система, в которой масса m движется
по горизонтали. направлении, а x — перемещение, измеренное от положения статического
равновесия масса. Перемещение x является обобщенной координатой, а число степеней
свободы система равна 1.
Когда маятник, состоящий из безмассового стержня
длины L и точки массы M, прикрепленный к бруску
массы m (рис. 3.12b), одной координаты перемещения
x недостаточно, чтобы описать движение системы. С
одной стороны маятник движется вместе с блоком в
горизонтальном направлении. С другой стороны,
маятник вращается, и вращательное движение может
быть описано с помощью углового смещения θ.
Таким образом, для системы на рис3.12b x и θ — это
две независимые обобщенные координаты, а число
степеней свободы системы равно 2.
Рис. 3.12. Механическая система с (а) перемещением в качестве
обобщенной координаты и (b) перемещениями типами
обобщенных координат.

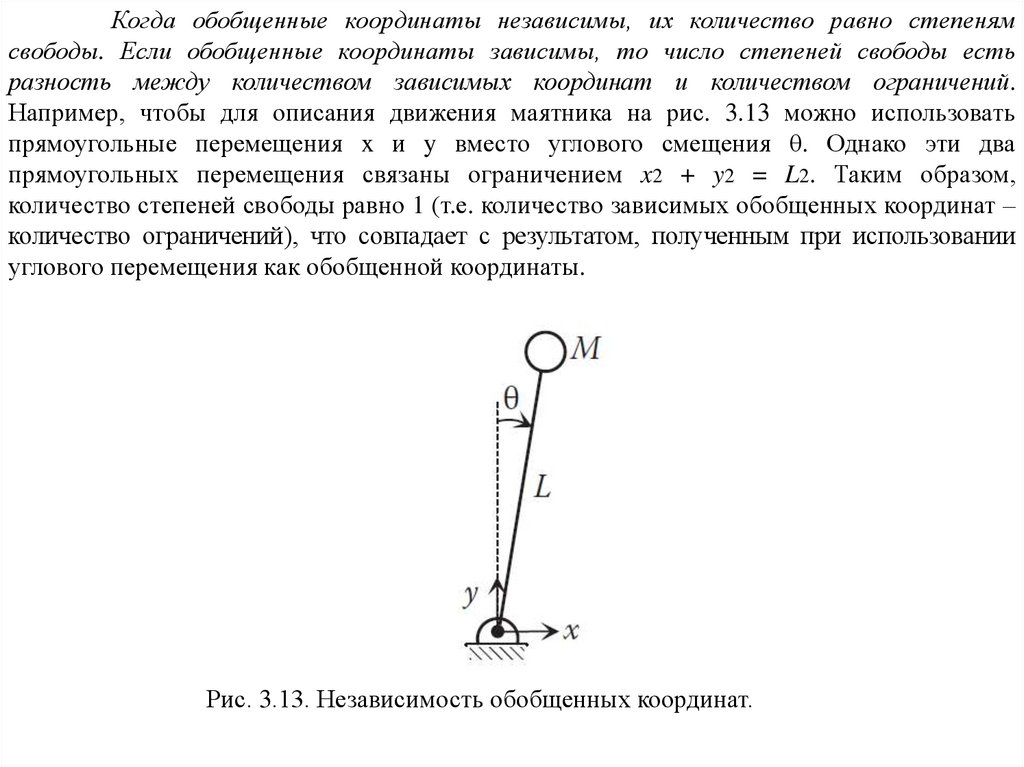
67.

Когда обобщенные координаты независимы, их количество равно степеням
свободы. Если обобщенные координаты зависимы, то число степеней свободы есть
разность между количеством зависимых координат и количеством ограничений.
Например, чтобы для описания движения маятника на рис. 3.13 можно использовать
прямоугольные перемещения x и y вместо углового смещения θ. Однако эти два
прямоугольных перемещения связаны ограничением x2 + y2 = L2. Таким образом,
количество степеней свободы равно 1 (т.е. количество зависимых обобщенных координат –
количество ограничений), что совпадает с результатом, полученным при использовании
углового перемещения как обобщенной координаты.
Рис. 3.13. Независимость обобщенных координат.

68.

Второй закон Ньютона
Второй закон Ньютона гласит, что ускорение массы пропорционально вектору
равнодействующей сил действующих на него и происходит в направлении действия этой
силы. Предположим, что поступательное движение частицы или твердого тела ограничено
в плоскости. Для частицы, представляющей собой массу пренебрежимо малых размеров,
Второй закон Ньютона можно представить в векторной форме.
или в скалярной форме
где ΣFx и ΣFy — суммы приложенных сил, разложенных по направлениям x и y,
соответственно, а ах и ау - x и y компоненты ускорения частицы соответственно. Для
твердого тела второй закон Ньютона имеет вид
где нижний индекс C обозначает центр масс. Во многих инженерных приложениях
гравитационное поле считается однородным, а центр масс совпадает с центром тяжести.

69.

Диаграммы свободного тела
Чтобы применить второй закон Ньютона к механической системе, полезно
нарисовать диаграмму свободного тела для каждой массы в системе, показывая все
внешние силы. Не вводимые силы могут быть описаны в терминах перемещений или
скоростей с использованием выражений, связанных с пружиной или демпфер. Построение
правильных диаграмм свободного тела — самый важный шаг в анализе механических
системы.
Рассмотрим простую систему масса-пружина-демпфер,
на которую действует входная сила f, как показано на
рисунке 3.14:
1) Составить дифференциальное уравнение движения
используя второй закон ньютона;
2) Определить передаточную функцию системы,
допустив, что начальное перемещение и скорость
равны нулю ;
3) Используя Simulink и Simscape, построить блоксхемы, чтобы найти выход перемещение x(t) системы,
на которую действует приложенная сила f(t) = 10u(t),
где u(t) — единичная ступенчатая функция. Значения
параметров: m = 1 кг, b = 2 Н·с/м, k = 5 Н/м.
Рис. 3.14. Система масса-пружинаПредположим, что Начальные условия нулевые.
демпфер: (а) физическая система и
(b) диаграмма свободного тела.

70.

Дифференциальные уравнения системы согласно второму Ньютона имеют вид:
которое можно преобразовать в стандартную форму дифференциального уравнения вводавывода
Преобразование Лапласа обеих частей с нулевыми начальными условиями приводит к
Таким образом, передаточная функция, связывающая вход f(t) с выходом x(t), равна

71.

Уравнение состояния, вход и выход имеют вид:
Таким образом, уравнения переменной состояния формируются как
Выходное уравнение
Запись уравнений переменной состояния и выходного уравнения в матричной форме дает

72.

Рис. 3.15. Модели и их переходные
процессы

73.

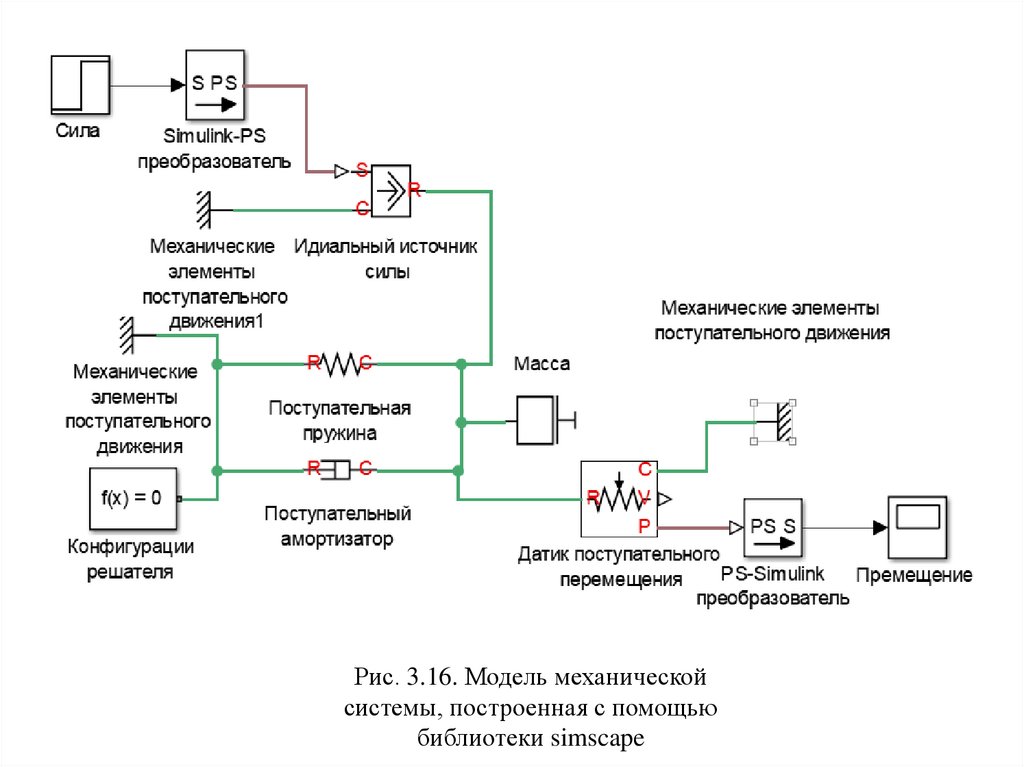
Рис. 3.16. Модель механической
системы, построенная с помощью
библиотеки simscape

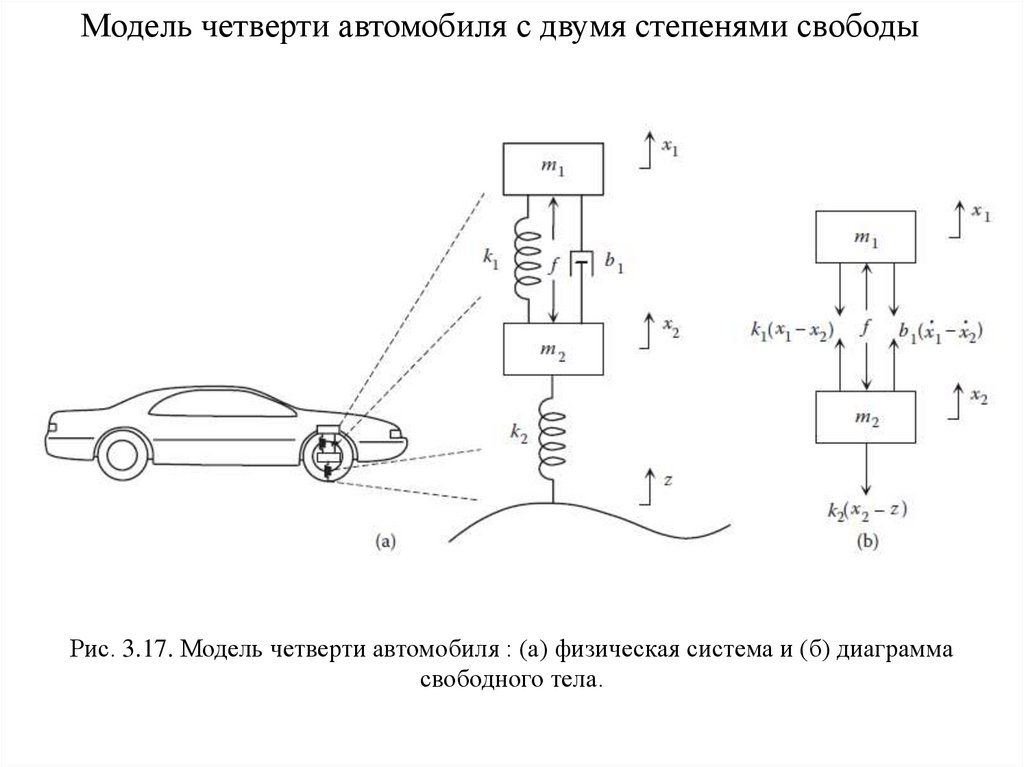
74.

Модель четверти автомобиля с двумя степенями свободы
Рис. 3.17. Модель четверти автомобиля : (а) физическая система и (б) диаграмма
свободного тела.

75.

Электрические цепи
Электрические системы или электрические цепи обычно можно рассматривать
как соединения сосредоточенных элементов, такие как источники, резисторы, катушки
индуктивности и конденсаторы. Источниками являются активные электрические
элементы, которые могут снабжать цепь энергией и служить входами. Резисторы,
катушки индуктивности и конденсаторы могут накапливать или рассеивать энергию,
доступную в цепи. Элементы которые не могут производить энергию называют
пассивными электрическими элементами. Две основные переменные, используемые для
описания
Двумя основными переменными, используемыми для описания динамического
поведения электрической цепи, являются ток и напряжение. Ток – скорость изменения
заряда во времени,
где q — заряд в кулонах (Кл), а i — ток в амперах (А).
Напряжение в точке цепи является мерой разности электрических потенциалов
между заданной точкой и точкой отсчета, называемой землей. Единицей напряжения
является вольт (В).

76.

Рис. 4.1. Двухполюсный электрический элемент.
Рис. 4.2. Активные электрические элементы: (а) идеальный источник
напряжения и (б) идеальный источник тока.
Мощность, подаваемая на пассивный элемент или генерируемый активным элементом

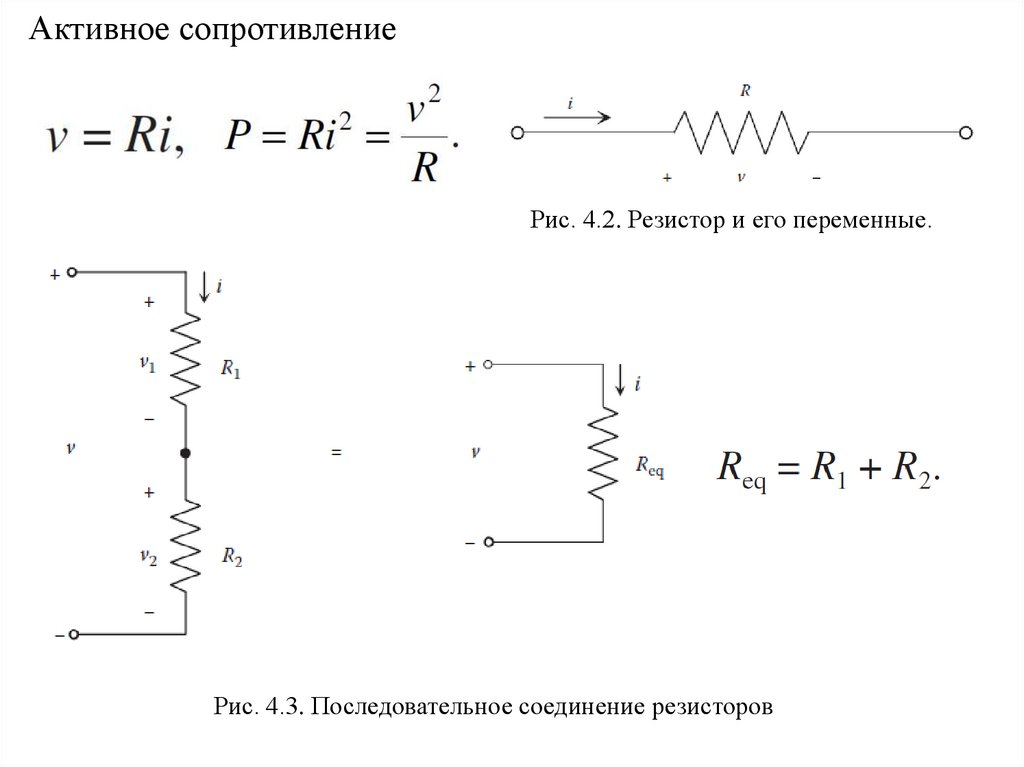
77.

Активное сопротивление
Рис. 4.2. Резистор и его переменные.
Рис. 4.3. Последовательное соединение резисторов

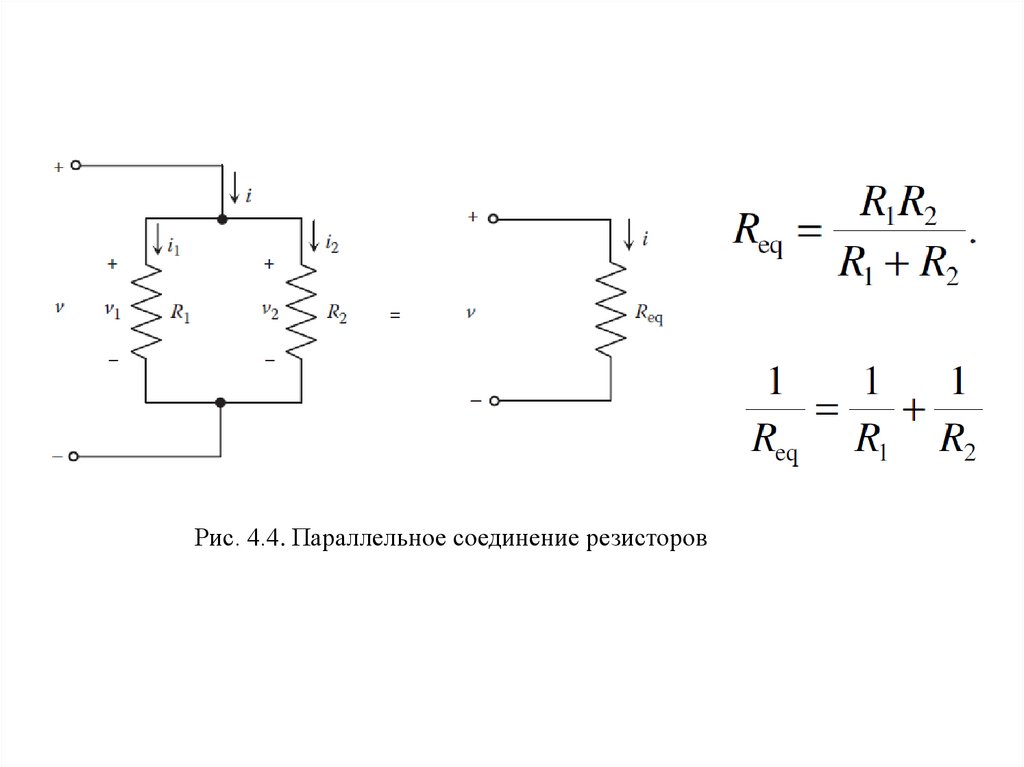
78.

Рис. 4.4. Параллельное соединение резисторов

79.

Индуктивность
На рис. 6.6 показан символ катушки индуктивности. Соотношение напряжение-ток для
линейного индуктора:
Рис. 4.5. Катушка индуктивности
Энергия, подводимая к индуктору, сохраняется в его магнитном поле. Запасенная
энергия может быть полученный путем интегрирования мощности
В уравнении предполагается, что ток через катушку индуктивности равен нулю
при t = 0. Обратите внимание, что энергия, запасенная в катушке индуктивности, зависит
от квадрата тока через катушку индуктивности и не зависит от того, как направлен ток.

80.

Емкость
На рис. 4.6. показано обозначение конденсатора, где С — емкость в фарадах (Ф). Емкость
— это мера того, сколько заряда может храниться на обкладках конденсатора в
зависимости от заданного напряжения, а математическое описание имеет вид: q = Cv или
v = q/C. Таким образом, зависимость напряжения от тока для конденсатора имеет вид
выражается как
Рис. 4.6. Конденсатор
В уравнении предполагается, что напряжение на конденсаторе равно нулю при t = 0.
Обратите внимание, что энергия, запасенная в конденсаторе, зависит от квадрата
напряжения на конденсаторе и не зависит от полярности напряжения.

81.

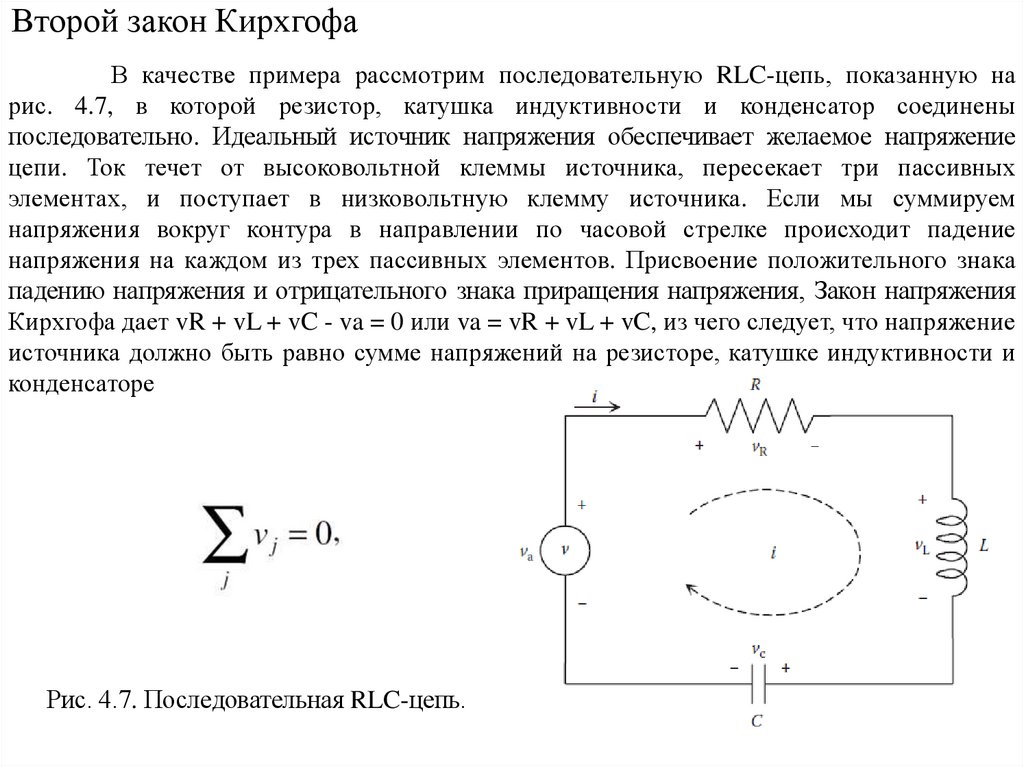
Второй закон Кирхгофа
В качестве примера рассмотрим последовательную RLC-цепь, показанную на
рис. 4.7, в которой резистор, катушка индуктивности и конденсатор соединены
последовательно. Идеальный источник напряжения обеспечивает желаемое напряжение
цепи. Ток течет от высоковольтной клеммы источника, пересекает три пассивных
элементах, и поступает в низковольтную клемму источника. Если мы суммируем
напряжения вокруг контура в направлении по часовой стрелке происходит падение
напряжения на каждом из трех пассивных элементов. Присвоение положительного знака
падению напряжения и отрицательного знака приращения напряжения, Закон напряжения
Кирхгофа дает vR + vL + vC - va = 0 или va = vR + vL + vC, из чего следует, что напряжение
источника должно быть равно сумме напряжений на резисторе, катушке индуктивности и
конденсаторе
Рис. 4.7. Последовательная RLC-цепь.

82.

Пример - Последовательная цепь RLC: Рассмотрим последовательную цепь RLC,
показанную на рис. 4.7. 1) Выведите дифференциальное уравнение относительно тока
контура i. 2) Определите передаточную функцию I(s)/Va(s), которая связывает напряжение
источника Va(t) с током i(t), текущем в контуре. Предположим, что все начальные условия
равны нулю. 3) Определите передаточную функцию VC(s)/Va(s), которая связывает
напряжение источника Va(t) с напряжение на конденсаторе VC(t). Предположим, что все
начальные условия равны нулю.
Для последовательного контура через каждый элемент протекает один и тот же
ток. Выразим для VR,VL и VC
Тогда
Обратите внимание, что приведенное выше уравнение является
интегро-дифференциальным
уравнением,
а
не
дифференциальным
уравнением.
Чтобы
исключить
интегральный член, мы берем производную по времени от
обеих частей уравнения. Преобразование приводит к
которое представляет собой дифференциальное уравнение
второго порядка

83.

Преобразование Лапласа приведенного выше дифференциального уравнения дает
Передаточная функция, связывающая входное напряжение Va(t) и выходной ток i(t),
имеет вид
Обратите внимание, что напряжение конденсатора VC не фигурирует явно в
дифференциальном уравнении. Определим передаточную функцию VC(s)/Va(s), используем
результат передаточной функции I(s)/Va(s)и применим соотношение напряжение-ток для
конденсатора
Таким образом, передаточная функция, связывающая входное напряжение va(t) и
напряжение конденсатора VC(t), имеет вид

84.

Электрические цепи
Первый закон Кирхгофа
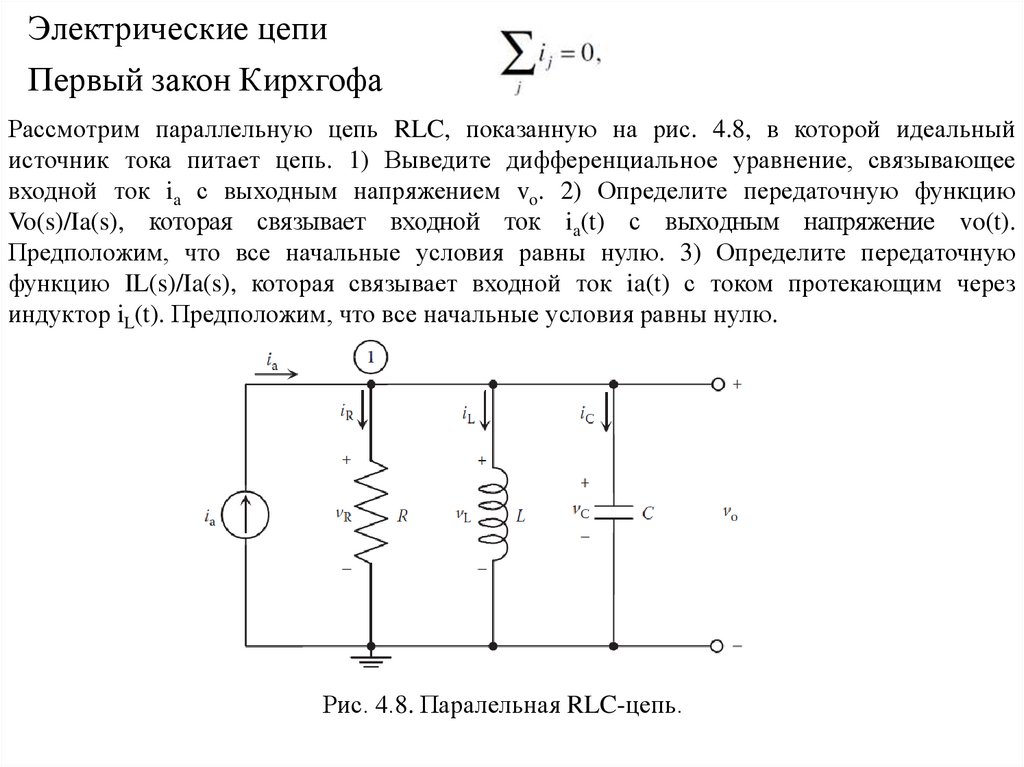
Рассмотрим параллельную цепь RLC, показанную на рис. 4.8, в которой идеальный
источник тока питает цепь. 1) Выведите дифференциальное уравнение, связывающее
входной ток ia с выходным напряжением vo. 2) Определите передаточную функцию
Vo(s)/Ia(s), которая связывает входной ток ia(t) с выходным напряжение vo(t).
Предположим, что все начальные условия равны нулю. 3) Определите передаточную
функцию IL(s)/Ia(s), которая связывает входной ток ia(t) с током протекающим через
индуктор iL(t). Предположим, что все начальные условия равны нулю.
Рис. 4.8. Паралельная RLC-цепь.

85.

Тогда мы имеем
которое является интегро-дифференциальным уравнением.
интегральный член, мы продифференцируем обе части
преобразования получим
Чтобы исключить
уравнения. После
которое представляет собой дифференциальное уравнение второго порядка для выходного
напряжения vo(t).
Преобразование Лапласа приведенного выше дифференциального уравнения дает
Передаточная функция, связывающая входной ток ia(t) и выходное напряжение vo(t), имеет
вид

86.

Чтобы найти передаточную функцию IL(s)/Ia(s), обратите внимание, что
Тогда
Приведенные выше два простых примера иллюстрируют, как можно составить
дифференциальное уравнение для последовательно или параллельной RLC цепи с
использованием закона напряжения Кирхгофа или закона тока Кирхгофа. Однако, если
схема компоненты последовательно соединены в одних частях и параллельны в других, мы
должны избирательно применять Закон напряжения Кирхгофа и закон тока Кирхгофа,
чтобы получить желаемое дифференциальное уравнение.

87.

ЭЛЕКТРОМЕХАНИЧЕСКИЕ СИСТЕМЫ
Многие полезные устройства, такие как моторы, генераторы, динамики, микрофоны и
акселерометры, построены путем объединения электрических элементов и механических
элементов. Для таких электромеханических систем, мы должны применять как
электрические принципы (например, законы Кирхгофа), так и механические
принципы(например, второй закон Ньютона) для разработки динамической модели
системы. В этом разделе мы обсуждим моделирование двигателей постоянного тока (DC),
которые могут генерировать силы или крутящие моменты с помощью электрических
подсистем и являются важными исполнительными механизмами в системах управления.
В различных электромеханических системах электрические и механические подсистемы
связаны магнитное поле. На рис. 5.1 показан двигатель постоянного тока, который
состоит из основных элементов (включая статор, ротор, якорь и коллектор).
Рис. 5.1 Щеточный двигатель постоянного тока.

88.

Для простоты сначала рассмотрим провод, по которому течет ток в магнитном поле.
Предполагать, что провод представляет собой либо прямой проводник, перпендикулярный
к однородному магнитному полю, либо круговой проводник в радиальном магнитном поле.
Это две распространенные ситуации во многих приложениях. Потомна провод будет
действовать сила, и соотношение между силой f и током i равно
где B — плотность магнитного потока в теслах (1 Тл = 1 Вб/м2), а L — длина проводника
в магнитное поле. Направление силы можно определить с помощью правила правой руки,
как показано на рисунке 5.2а. Согните четыре пальца от положительного направления
тока к положительному направлению магнитное поле, а большой палец будет указывать
на положительное направление силы. Если проводник движется относительно магнитного
поля, то в проводнике будет индуцироваться напряжение.
Рис. 5.2 Направление (а) силы, действующей на проводник, и (б) напряжения,
индуцируемого в движущемся проводнике.

89.

На рис. 5.2б показан прямой проводник, движущийся вверх в магнитном поле.
Предположим, что направление движения перпендикулярно направлению магнитного поля.
Тогда скаляр связи между наведенным напряжением eb и скоростью v проводника есть
где Kt = nBLr — постоянная момента двигателя. Обратите внимание, что линейная
скорость катушек пропорциональна угловой скорости, v = ωr. Тогда, согласно уравнению,
противо-ЭДС, генерируемая в якоре за счет вращательного движения
где Ke = nBLr — постоянная противо-ЭДС двигателя. Две константы, Kt и Ke, имеют
одинаковые значения. Данные уравнения используются для моделирования связи между
электрическими и механическими подсистемы двигателя постоянного тока. Два основных
типа двигателей постоянного тока, двигатели постоянного тока с управлением током якоря
и двигатели постоянного тока с управлением полем.

90.

Математическая модель двигателя состоит из электрической и механической частей,
описываемых системой уравнений:
Первое уравнение системы (1) - баланс напряжений в электрической части двигателя.
Второе - уравнение движения для механической части. Третье и четвертое - уравнения
связи электрической и механической частей двигателя. ua - напряжение источника
питания, подаваемое на электрическую часть якоря двигателя (1 – подано номинальное
напряжение, 0 – отключено); ea - ЭДС, наводимая в обмотке якоря при пересечении
проводников потока φ, создаваемого неподвижными полюсами; ia - электрический ток в
якорной цепи; ra - полное электрическое сопротивление якорной цепи, включая
сопротивление дополнительных полюсов и щеток; Та- постоянная времени якорной цепи;
m, mс - электромагнитный и статический моменты; ω - скорость вращения якоря; φ - поток
полюсов; Tj - инерционная постоянная времени двигателя. Параметры двигателя:
ra = 0,107; Ta = 0,034; Tj =0,72; φ = 1/

91.

Модель ДПТ НВ в Matlab-Simulink
Произведем прямое преобразование Лапласа дифференциального уравнения ДПТ НВ.
Из первого уравнения слагаемые с токами ia перенесем в левую часть, а ЭДС ea и
напряжение ua - в правую:
Далее вынесем за скобки
и определим ток :

92.

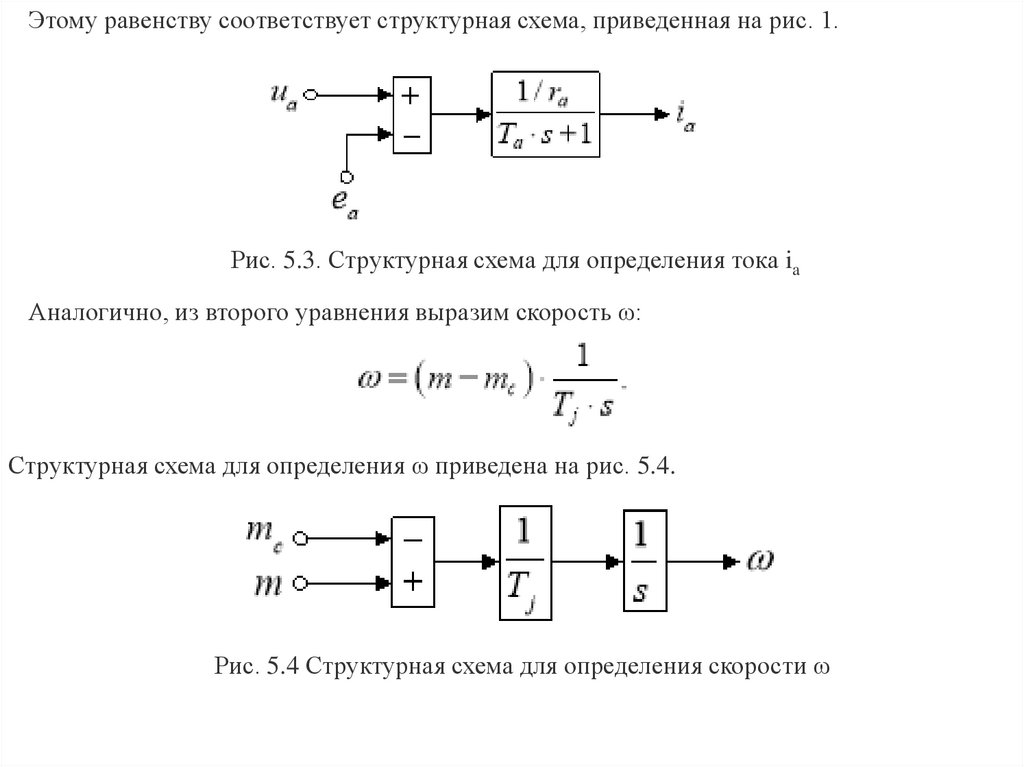
Этому равенству соответствует структурная схема, приведенная на рис. 1.
Рис. 5.3. Структурная схема для определения тока ia
Аналогично, из второго уравнения выразим скорость ω:
Структурная схема для определения ω приведена на рис. 5.4.
Рис. 5.4 Структурная схема для определения скорости ω

93.

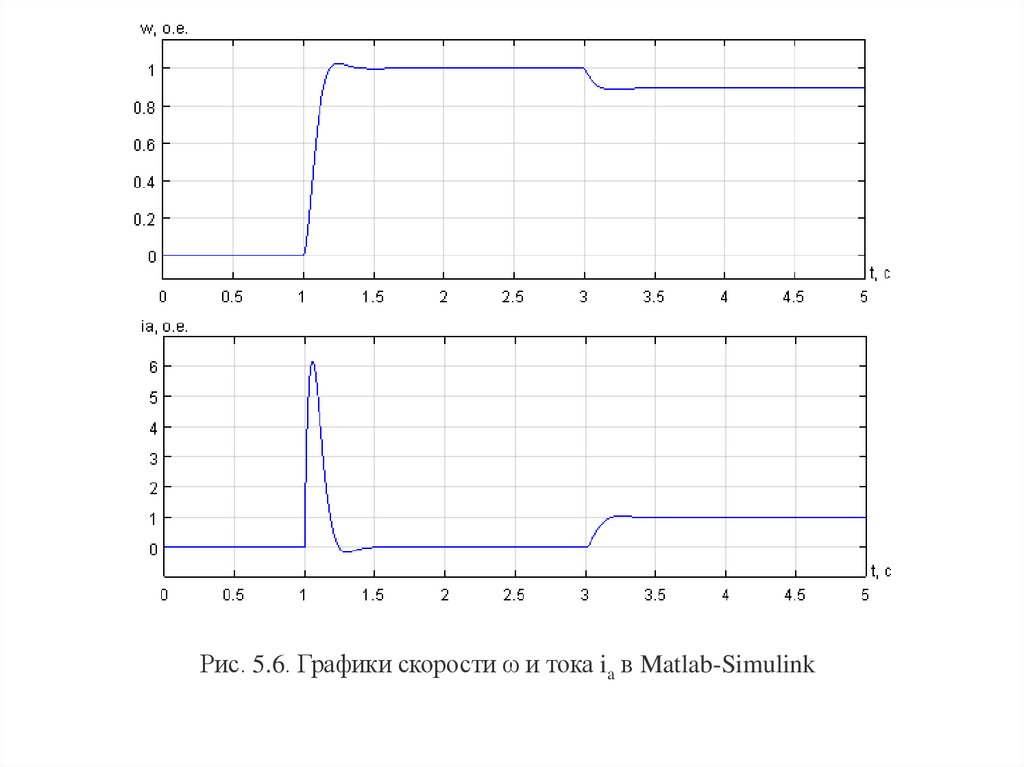
Математическая модель ДПТ НВ в Matlab-Simulink представлена на рис. 5.5.
Рис. 5.5. Математическая модель ДПТ НВ в Matlab-Simulink

94.

Рис. 5.6. Графики скорости ω и тока ia в Matlab-Simulink