Похожие презентации:
Описание линейных непрерывных САР. (Тема 1)
1.
ОПИСАНИЕ ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ САРПонятие оператора
Оператор – любое соответствие между функциями одного множества и
функциями другого множества
A
Например (рис. а), пусть A – оператор,
отражающий коэффициент передачи
(усиления) некоторого устройства
а)
A k
x t X
y t Y
x, y
y(t)=k*x(t)
x(t)
t
0
б)
Оператор A связывает все входные функции
x(t) с выходными y(t), воздействуя на
входной сигнал (умножая его в каждый
момент времени на коэффициент k, т.е.
усиливая его). Такое звено в результате
формирует выходную функцию y(t),
отличающуюся от входной x(t) на
постоянный множитель (рис. б).
Понятие оператора широко используется в
ТАУ.
2.
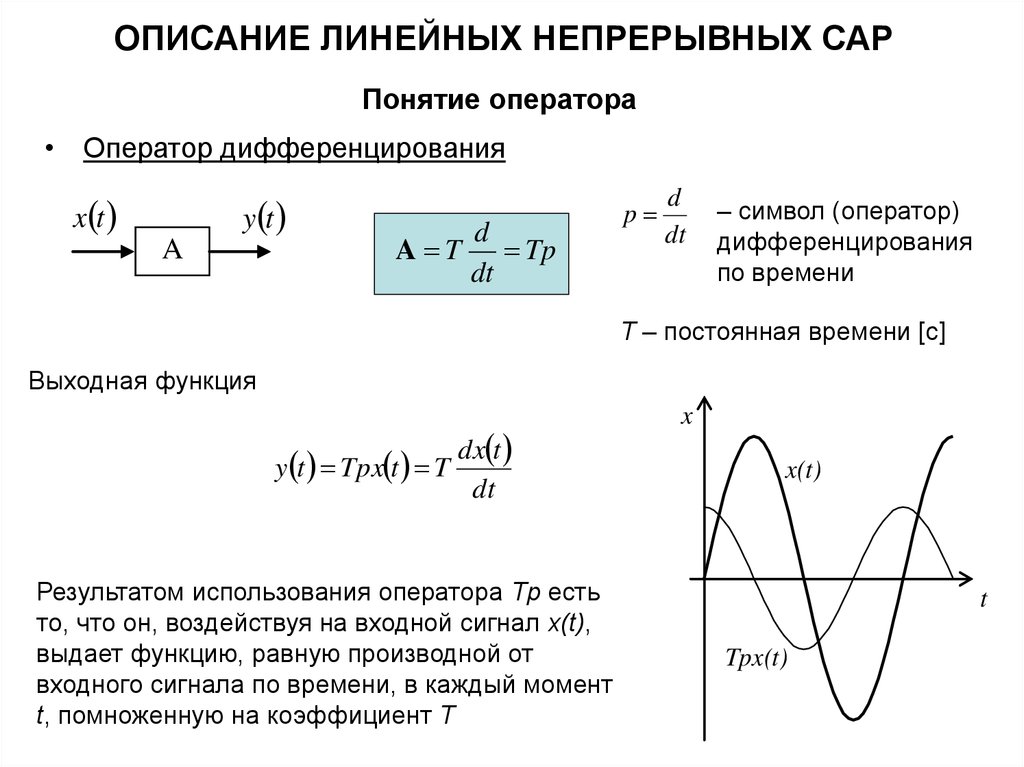
ОПИСАНИЕ ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ САРПонятие оператора
• Оператор дифференцирования
x t
y t
A
A T
d
Tp
dt
p
d
dt
– символ (оператор)
дифференцирования
по времени
T – постоянная времени [c]
Выходная функция
y t Tpx t T
dx t
dt
Результатом использования оператора Tp есть
то, что он, воздействуя на входной сигнал x(t),
выдает функцию, равную производной от
входного сигнала по времени, в каждый момент
t, помноженную на коэффициент T
x
x(t)
t
Tpx(t)
3.
ОПИСАНИЕ ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ САРПонятие оператора
• Оператор интегрирования
x t
p 1
y t
A
A
1 1
dt
Tp T
Выходная функция
y t
1
1
x t x t dt
Tp
T
Результатом использования оператора
интегрирования есть то, что он,
воздействуя на входной сигнал x(t),
выдает для каждого нового значения t,
новое значение площади.
1
– символ (оператор)
p интегрирования
T – постоянная времени [c]
1
x(t)
Тр
x
t
x(t)
4.
Математические модели системДля того чтобы изучить свойства сложной физической системы и
научиться управлять ей, необходимо получить ее математическую модель. Для
этого
требуется
установить
все
взаимосвязи
между
переменными,
характеризующими поведение системы.
Поскольку все реальные
динамическими,
то
для
их
дифференциальные уравнения.
системы по своей природе являются
описания
естественно
использовать
Если эти уравнения могут быть линеаризованы, то тогда можно
воспользоваться преобразованием Лапласа.
В действительности, сложность системы и игнорирование ряда факторов обуславливают возникновение некоторых допущений, связанных с
функционированием данной системы. Поэтому часто бывает полезным игнорировать эти допущения и произвести линеаризацию системы.
В результате на основании физических законов, описывающих поведение
эквивалентной
линейной
системы,
мы
можем
получить
систему
дифференциальных уравнений.
Наконец, используя математический аппарат (преобразование Лапласа),
сможем получить решение, характеризующее поведение данной системы.
5.
Математические модели системДифференциальные уравнения, описывающие динамику физической
системы, получаются на основании фундаментальных физических законов. Этот
метод в равной степени применим к механическим, электрическим,
гидравлическим и термодинамическим системам.
i t
Механический амортизатор (автомобильный)
описывается вторым законом Ньютона
R
L
С
u t
Согласно второму закону Кирхгофа
du t u t 1
C
u t dt i t
dt
R L0
t
Трение
Масса
о стенки, b
m
y
F t
Динамика массы m описывается
диф. уравнением:
d 2 y t
dy t
m
b
ky t F t
2
dt
dt
k – коэффициент упругости пружины;
b – коэффициент трения;
v t
dy t
dt
- скорость
dv t
m
bv t k v t dt F t
dt
0
t
Уравнения эквивалентны – системы подобные
6.
ОПИСАНИЕ ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ САРМатематическое определение линейных САР
Для линейных САР, в отличие от нелинейных, справедлив принцип суперпозиции
g(t)
A
x(t)
Пусть известно, что
реакцией САР на воздействие g1(t) является сигнал x1(t)=Ag1(t),
реакцией САР на воздействие g2(t) является сигнал x2(t)=Ag2(t),
…
реакцией САР на воздействие gn(t) является сигнал xn(t)=Agn(t).
САР является линейной, если ее реакция на линейную комбинацию функций
(сигналов) gi(t), i=1,2,…,n
g t k1 g1 t k 2 g 2 t k n g n t
где ki – произвольные
действительные числа
является также линейной комбинацией сигналов xi(t), i=1,2,…,n:
x t k1 x1 t k 2 x2 t k n xn t A k1 g1 t k 2 g 2 t k n g n t
Признаки линейной системы:
1. Реакция линейной САР на сумму сигналов равна сумме реакций на каждый
сигнал в отдельности.
2. Если все элементы САР являются линейными, то и САР в целом будет
линейной.
7.
ОПИСАНИЕ ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ САРЛинеаризация динамических САР
Пусть процессы в реальной САР (как в установившихся, так и в переходных
режимах) описывается нелинейным уравнением динамики:
F x, y , z 0
x, y и z – переменные состояния, воздействия на САР,
либо их производные.
В установившемся режиме уравнение принимает вид (уравнение статики):
F x0 , y0 , z0 0
x0, y0 и z0 – значения воздействий в установившемся
режиме
В реальном режиме, близкому к заданному установившемуся
x x0 x
y y0 y
z z0 z
Подстановка этих выражений в исходную функцию (уравнение динамики),
после разложения в ряд Тейлора и пренебрежения составляющими высших
порядков малости дает
F x, y, z F x0 , y0 , z0
F
x
x
x x0
F
y
y
y y0
F
z
z z0
z F x0 , y0 , z0 F x, y, z
8.
ОПИСАНИЕ ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ САРЛинеаризация динамических САР
Вычитая это уравнение из уравнения статики, получают линеаризованное
уравнение САР в приращениях:
F x, y, z 0
После указанных преобразований САР считается линейной.
x
x
O1
x=f(g)
g
g
O
Геометрический смысл линеаризации
(на примере функции одной
переменной) состоит в замене
исходной кривой касательной в точке
О1, соответствующей заданному
режиму работы, и параллельном
переносе начала координат в эту точку.
После линеаризации символы
приращений переменных обычно
опускают.
9.
10.
Преобразование ЛапласаДифф.
ур-ние
1
решение во временной области
L
Алгебр.
ур-ние
x(t)
L-1 3
решение в s-области
2
X(s)
11.
ОПИСАНИЕ ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ САРПреобразование Лапласа
Преобразованием Лапласа называют соотношение:
F p L f t f t e pt dt
0
которое ставит функции f(t) действительного переменного в соответствие
функцию F(p) комплексного переменного p j
Функция f(t), подвергающаяся преобразованию Лапласа, называется
оригиналом, и должна обладать следующими свойствами:
• f(t) определена и кусочно-дифференцируема на интервале 0;
f t Mect
• f(t) 0 при t<0;
• существуют такие положительные числа c и M, что при любом 0 t ∞ выполняется неравенство
Функция F(p) называется изображением. Оператор L называют оператором
преобразования Лапласа.
Обратным преобразованием Лапласа называют соотношение:
j
1
f t L F p
F p e pt dp
2 j j
1
определяющее по известному изображению его
оригинал
L-1 – оператор обратного преобразования Лапласа.
Обратное преобразование Лапласа обычно находят путем разложения F(p) на простые дроби с
помощью правила Хевисайда. Этот метод полезен при анализе и синтезе систем управления, т.к.
позволяет легко выявить влияние каждого корня характеристического уравнения системы.
12.
ОПИСАНИЕ ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ САРПреобразование Лапласа
Все физически реализуемые сигналы имеют преобразование Лапласа.
Название функции
1
Единичная ступенчатая
функция
t
Преобразования Лапласа [6]
Название
f(t)
F(p)
f(t)
функции
1
1 t
Синусоида
sin bt
p
Единичная импульсная
t
функция
1
Косинусоида
cos bt
1
Затухающая
синусоида
e at sin bt
t
Единичная линейная
функция
t
t
n
Степенная функция
t
Экспонента
at
Экспонента n-го
порядка
e
2
p
n!
p n 1
Затухающая
косинусоида
1
p a
Расходящаяся
синусоида
n!
t n e at
p a n 1
Расходящаяся
косинусоида
e
at
F(p)
b
p2 b2
p
p2 b2
b
p a 2 b 2
p a
cos bt
t sin bt
t cos bt
p a 2 b 2
p
2bp
2
b
2 2
p2 b2
p
2
b2
2
13.
ОПИСАНИЕ ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ САРПреобразование Лапласа
Теоремы преобразования Лапласа [6]
Название операции
Умножение
оригинала на
коэффициент k
Сумма
Производная
Производная
n-го порядка
Интеграл
Формулировка теоремы
L k f t k F p ,
k=const
L f1 t f 2 t F1 p F2 p
df t
L
pF s f 0
dt
df n t
n
n 1
L
p
F
s
p
f 0
n
dt
p n 2 f 0 f n 1 0
t
F p
L f d
p
0
Название
операции
Формулировка теоремы
Чистое
запаздывание
L f t 1 t t 0 e t0 p F p
lim f t lim pF p
Начальное
значение
t 0
s
lim f t lim pF p
Конечное
значение
t
Умножение оригинала на
экспоненту
s 0
L e at f t F p a
t
L F1 p F2 p f1 t f 2 d
-1
Интеграл
свертки
0
t
f1 f 2 t d
0
14.
Преобразование ЛапласаМеханический амортизатор
Динамика массы m описывается дифф. уравнением:
d 2 y t
dy t
m
b
ky t f t
2
dt
dt
Трение
Масса
о стенки, b
m
Необходимо получить решение этого уравнения, т.е. выражение y(t).
y
dy 0
m p 2Y p py0
b pY p y0 kY p F p
dt
f t
Если f t 0
Преобразование Лапласа для этого уравнения имеет вид:
получим:
mp 2Y p mpy0 bpY p by0 kY p 0
H p
mp bp k Q p
Если полином Q(p) приравнять к нулю, то получим характеристическое уравнение. Его корни определяют
характер движения системы. Корни характеристического уравнения также называют полюсами системы.
Корни полинома H(p) называют нулями системы.
Выражая Y(p) получим:
Y p
mp b y0
Например, выражение Y(p) имеет нуль
2
p b m
В полюсах функция Y(p) обращается в бесконечность, а в
нулях она становится равной нулю. Расположение
полюсов и нулей на комплексной плоскости определяет
характер собственного (свободного) движения системы.
Когда
k m 2
b m 3
Y p
p 3 y0
p 1 p 2
Расположение полюсов и нуля на комплексной плоскости
15.
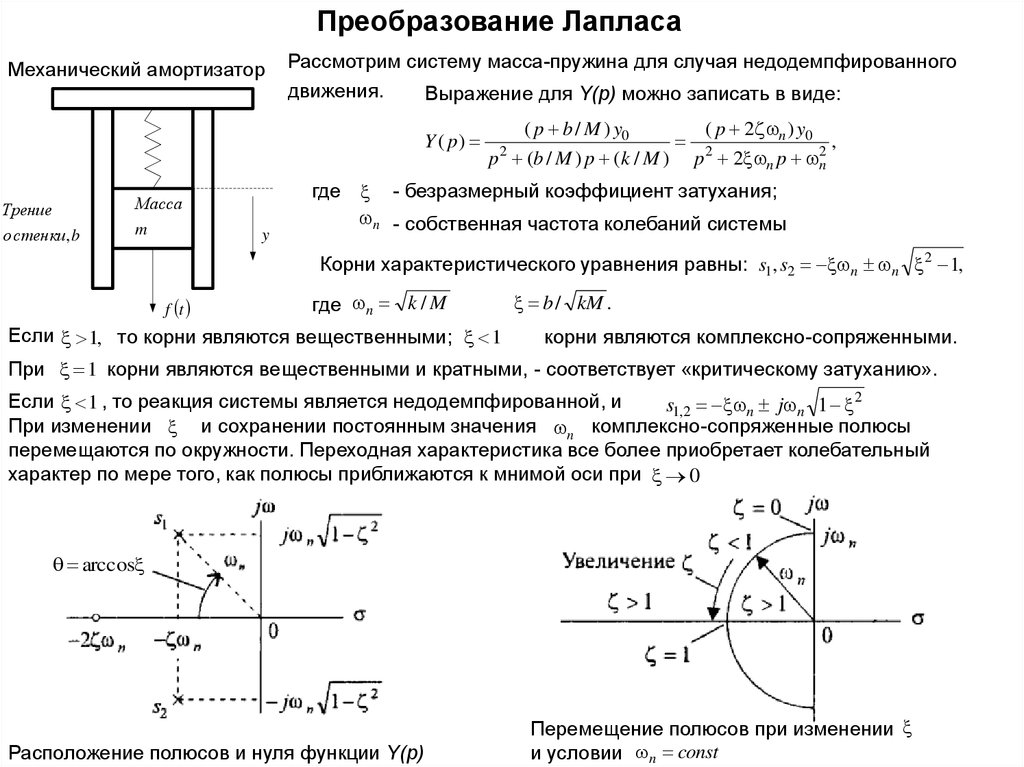
Преобразование ЛапласаМеханический амортизатор
Рассмотрим систему масса-пружина для случая недодемпфированного
движения.
Выражение для Y(p) можно записать в виде:
Y ( p)
Трение
Масса
о стенки, b
m
y
( p b / M ) y0
( p 2 n ) y0
2
,
p (b / M ) p (k / M ) p 2 n p 2n
2
где - безразмерный коэффициент затухания;
n - собственная частота колебаний системы
Корни характеристического уравнения равны: s1, s2 n n 2 1,
f t
где n k / M
Если 1, то корни являются вещественными; 1
b / kM .
корни являются комплексно-сопряженными.
При 1 корни являются вещественными и кратными, - соответствует «критическому затуханию».
Если 1 , то реакция системы является недодемпфированной, и
s1,2 n j n 1 2
При изменении и сохранении постоянным значения n комплексно-сопряженные полюсы
перемещаются по окружности. Переходная характеристика все более приобретает колебательный
характер по мере того, как полюсы приближаются к мнимой оси при 0
arccos
Расположение полюсов и нуля функции Y(p)
Перемещение полюсов при изменении
и условии n const
16.
Преобразование ЛапласаМеханический амортизатор
Решение можно получить с помощью таблицы обратного преобразования
Лапласа
1 2 ,
Введя обозначение
Трение
Масса
о стенки, b
m
y
f t
y (t ) k1e p1t k2e p2t
y0
2 1
y0
1 2
2
получим:
(e j ( / 2)e n t e j n t e j ( / 2 )e n t e j n t )
e j n t sin( n 1 2 t )
Переходные характеристики для случаев
передемпфированной ( 1 ) и
недодемпфированной ( 1 ) системы
Переходной характеристике при 1 свойственно уменьшение со временем амплитуды колебаний,
поэтому она носит название затухающих колебаний.
17.
ОПИСАНИЕ ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ САРПередаточная функция
Передаточной функцией САР называется отношение изображения выходной
переменной к изображению входной переменной при нулевых начальных
условиях.
Пусть САР описывается ДУ:
где
u t – входное воздействие;
Q p x t H p u t
П.ф. системы однозначно
описывает динамическую связь
между переменными.
x t – выходная переменная;
H p b0 b1 p b2 p 2 bm p m – оператор воздействия;
p – оператор
дифференцирования
Q p a0 a1 p a2 p 2 an p n – собственный оператор САР.
Применим к обеим частям этого уравнения преобразование Лапласа,
используя свойство линейности преобразования:
a0L x a1L x a2L x an L x n b0 L u b1L u b2 L u bmL u m
При нулевых начальных условиях
a
0
a1 p a2 p 2 an p n X p b0 b1 p b2 p 2 bm p m U p
Отсюда находим передаточную функцию (п.ф.)
X p b0 b1 p b2 p 2 bm p m
W p
U p a0 a1 p a2 p 2 an p n
p – комплексная
переменная
18.
ОПИСАНИЕ ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ САРПередаточная функция
Параметры передаточной функции
X p b0 b1 p b2 p 2 bm p m
W p
U p a0 a1 p a2 p 2 an p n
П.ф. системы описывает поведение
системы в терминах вход-выход и не
несет никакой информации о
внутренних переменных и характере
их изменения.
Характеристический полином п.ф. – полином знаменателя Q(p);
Порядок п.ф. – степень полинома знаменателя n;
Относительный порядок п.ф. – разность n-m между порядком полиномов
знаменателя и числителя;
Нули п.ф. – значения переменной р, при которых п.ф. обращается в нуль, т.е.
корни уравнения
H(p)=0
Полюсы п.ф. – значения переменной р, при которых п.ф. обращается в
бесконечность, т.е. корни уравнения
Q(p)=0,
называемого характеристическим уравнением.
19.
ОПИСАНИЕ ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ САРПередаточная функция
Свойства передаточной функции
1. Можно показать, что п.ф. САР (или звена) равна отношению оператора
воздействия к собственному оператору после замены в указанных операторах
оператора дифференцирования на комплексную переменную р и сокращения
общих множителей в числителе и знаменателе (если таковые имеются):
X p H p b0 b1 p b2 p 2 bm p m
W p
U p Q p a0 a1 p a2 p 2 an p n
Данное утверждение справедливо только для стационарных САР.
2. П.ф. САР (или звена) не может иметь равные между собой нули и полюсы.
3. П.ф. САР (или звена) в общем случае не может служить математическим
описанием САР (при произвольных начальных условиях).
4. Для работоспособных ОУ и прочих элементов САР, а также для САР в целом
необходимым является выполнение условия физической реализуемости
m n
причем реально отношение равенства возможно лишь применительно к
отдельным элементам САР в случаях m=n=0 (реже 1, очень редко 2).
20.
Передаточная функцияМеханический амортизатор
Передаточная функция системы масса-пружина получается, если в
исходном уравнении все начальные условия положить равными нулю:
mp 2Y ( p) bpY ( p) kY ( p) F ( p)
Трение
Масса
о стенки, b
m
Откуда находим передаточную функцию
y
выход
Y ( p)
1
G ( p)
2
вход
F ( p) Mp bp k
f t
Передаточная функция RC-цепи получается путем записи в
операторной форме уравнений Кирхгофа относительно напряжений:
V1( p) ( R
1
) I ( p)
Cp
Выражая I(p) и подставляя его в V2(p), получим:
V ( p)
V2 ( p) I ( p)
1
Cp
1/ Cp
V1( p)
R 1/ Cp
Тогда передаточная функция будет иметь вид:
V ( p)
1
1
1/
G ( p) 2
где RC есть постоянная времени цепи.
V1( p) RCp 1 p 1 p 1/
Единственный полюс функции G(p) равен p 1/
П.ф. можно получить сразу, если рассматривать цепь, как обычный делитель напряжения:
V2 ( p)
Z 2 ( p)
где Z1( p) R
Z 2 ( p) 1/ Cp
V1 ( p) Z1( p) Z 2 ( p)
21.
ОПИСАНИЕ ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ САРМатематическое описание и передаточные функции двигателя
постоянного тока как объекта управления
Для математического описания САР выделяют
ее отдельные элементы, которые обладают
однонаправленными свойствами: выходной
сигнал формируется в зависимости от входного,
и не влияет на него. Согласно с таким
принципом однонаправленности, в САР можно
выделить следующие элементы:
1. Генератор (Г). В качестве входа
рассматриваем напряжение возбуждения UВГ, в
качестве выхода – ЭДС генератора ЕГ. Условно
записываем:
U
Е
ВГ
(вход выход)
2. Двигатель (Д):
ОУ
Г
Г
EГ
ТГ
АД
ОВГ
UТГ
+ ОВД –
UВГ
Г
УМ
ЕГ
3. Тахогенератор (ТГ):
UТГ
4. Усилитель мощности (УМ) считаем идеальным
(внутреннее сопротивление равно нулю):
UУ UВГ
5. Узел сравнения (электрическая цепь) (УС):
UУ = UЗ – UТГ – UK
6. Корректирующая цепь (КЦ):
ЕГ UK
Д
СК
RК
UУ
UЗ
–
U0
САР регулирования скорости ДПТ по схеме
«генератор – двигатель»
+
22.
ГенераторU ВГ
di
d
iВГ RВГ LВГ ВГ iВГ RВГ 2 z pWВГ
dt
dt
R
d
U ВГ ВГ 2 z pWВГ
k ВГ
dt
E Г k KГ Г
U ВГ
ОУ
Г
Г
1
TВГ p 1 E Г
kГ
J
T
Я TM
ТГ
ОВГ
di
dt
1
EГ
cД
RК
–
U0
САР регулирования скорости ДПТ по схеме
«генератор – двигатель»
+
U ТГ kТГ
U ВГ kУ UУ
Цепь корректирования
TK p 1 U K
СК
UУ
UЗ
Усилитель мощности
UУ U З U ТГ U K
+ ОВД –
УМ
Тахогенератор
Узел сравнения
UТГ
UВГ
d
M MC
dt
p 2 TM p 1
Д
EГ
АД
Двигатель
E Г E Д iR Я LЯ
TK pE Г
УС
UЗ
–
–
UУ
УМ
UВГ
Г
UK КЦ
UTГ
ТГ
Блок-схема САР
EГ
Д
23.
ГенераторU ВГ
1
TВГ p 1 E Г
kГ
W Г s
E Г s
kГ
U ВГ s TВГ s 1
Двигатель
T
Я TM
p 2 TM p 1
1 cД
1
E Г W Д s s
cД
E Г s TЯ TM s 2 TM s 1
Тахогенератор
WTГ s
U ТГ kТГ
UУ
–
–
УМ
UВГ
Г
EГ
Д
UK КЦ
UTГ
Усилитель мощности
U ВГ kУ UУ
U TГ s
kТГ
s
УС
UЗ
WУМ s
ТГ
Блок-схема САР
U BГ s
kУ
U У s
Узел сравнения
UУ U З U ТГ U K
U У s U З s U ТГ s U K s
–
Цепь корректирования
TK p 1 U K
TK pE Г
УС
UЗ(s)
U s
T s
WГ s K
K
E Г s TK s 1
UУ(s)
UВГ(s)
EГ(s)
WУМ(s)
WГ(s)
WД(s)
– U (s)
K
UTГ(s)
WК(s)
WТГ(s)
Структурная схема САР
(s)





















 Физика
Физика








