Похожие презентации:
Алгебра высказываний. Лекция 2
1.
ЛЕКЦИЯ 2. АЛГЕБРАВЫСКАЗЫВАНИЙ
2.
■ Логическое высказывание – это повествовательное предложение, относительнокоторого можно однозначно сказать, истинно оно или ложно. Высказывание не может
быть выражено повелительным или вопросительным предложением, оценка
истинности или ложности которых невозможна. Высказывания могут выражаться с
помощью математических, физических, химических и прочих знаков.
■ Умозаключение - форма мышления, посредством которой из одного или нескольких
суждений, называемых посылками, по определенным правилам вывода получаем
суждение-заключение (вывод умозаключения)
■ Предложения типа "В городе A более миллиона жителей", "У него голубые глаза" не
являются высказываниями, так как для выяснения их истинности или ложности
нужны дополнительные сведения: о каком конкретно городе или человеке идет речь.
Такие предложения называются высказывательными формами.
■ Высказывания имеют определенную логическую форму. Понятие о предмете мысли
называется субъектом и обозначается буквой S, а понятие о свойствах и отношениях
предмета мысли называется предикатом и обозначается буквой P. Оба эти понятия субъект и предикат называются терминами суждения.
Отношения между субъектом и предикатом выражается связкой «есть», «не
есть», «является», «состоит» и т.д.
■ Таким образом, каждое высказывание состоит из трех элементов субъекта, предиката и связки (двух терминов и связки). Состав суждения можно
выразить общей формулой «S есть P» или «S не есть P».
3.
■ Высказывательная форма — это повествовательное предложение, которое прямоили косвенно содержит хотя бы одну переменную и становится высказыванием,
когда все переменные замещаются своими значениями.
■ Алгебра логики рассматривает любое высказывание только с одной точки зрения
— является ли оно истинным или ложным. Заметим, что зачастую трудно
установить истинность высказывания. Так, например, высказывание "Площадь
поверхности Индийского океана равна 75 млн кв. км" в одной ситуации можно
посчитать ложным, а в другой — истинным. Ложным — так как указанное
значение неточное и вообще не является постоянным. Истинным — если
рассматривать его как некоторое приближение, приемлемое на практике.
4.
Употребляемые в обычной речи слова и словосочетания "не", "и", "или", "если . . . , то","тогда и только тогда" и другие позволяют из уже заданных высказываний строить новые
высказывания. Такие слова и словосочетания называются логическими связками.
Высказывания, образованные из других высказываний с помощью логических связок,
называются составными. Высказывания, не являющиеся составными, называются
элементарными (простыми).
Истинность или ложность получаемых таким образом составных высказываний зависит
от истинности или ложности элементарных высказываний.
Чтобы обращаться к логическим высказываниям, им назначают имена. Пусть через А
обозначено высказывание "Тимур поедет летом на море", а через В — высказывание
"Тимур летом отправится в горы". Тогда составное высказывание "Тимур летом
побывает и на море, и в горах" можно кратко записать как А и В. Здесь "и" —
логическая связка, А, В — логические переменные, которые мoгут принимать только два
значения — "истина" или "ложь", обозначаемые, соответственно, "1" и "0".
Каждая логическая связка рассматривается как операция над логическими
высказываниями и имеет свое название и обозначение: отрицание, конъюнкция,
дизъюнкция, импликация, эквивалентность.
Если составное высказывание выразить в виде формулы, в которую войдут логические
переменные и знаки логических операций, то получится логическое выражение,
значение которого можно вычислить. Значением логического выражения могут быть
только ЛОЖЬ или ИСТИНА.
5.
Логическое отрицаниеВ естественном языке ему соответствует выражение "неверно, что . . .", относящееся
ко всему высказыванию, или присоединение союза "не" к некоторой части простого
высказывания.
Например, высказывание "Число 10 – четное"= ИСТИНА, отрицанием его является
высказывание "Число 10 – нечетное"= ЛОЖЬ.
Или высказывание "Число 10 - отрицательное" = ЛОЖЬ, его отрицание "Неверно, что
число 10 - отрицательное" = ИСТИНА.
6.
Логическое умножение(Конъюнкция)В естественном языке ему соответствуют союзы "и“, “а“, “но". Применяется если в
тексте идут подряд независимые предложения
Например, из двух простых высказываний А="На улице светит солнце" и В="На улице
ясная погода" построим сложное, используя союз-связку "и".
Получим "На улице светит солнце и ясная погода".
7.
Логическое сложение (Дизъюнкция)В естественном языке ему соответствует союз "или".
Например, из двух простых высказываний А="На улице светит солнце" и В="На улице
пасмурная погода" построим сложное, используя союз-связку "или".
Получим "На улице светит солнце или пасмурная погода".
8.
Исключающее илиВ естественном языке ему соответствует связки "или", "либо … либо".
Например, из двух простых высказываний А=«Его зовут Петя" и В=" Его зовут Дима"
построим сложное, используя союз-связку "или".
Получим "Его зовут Петя или Дима".
9.
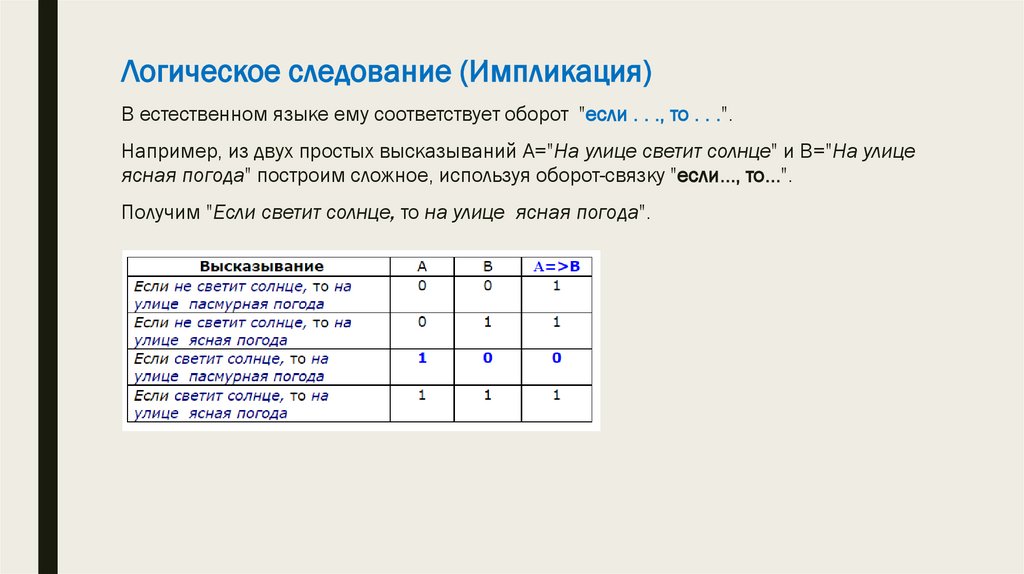
Логическое следование (Импликация)В естественном языке ему соответствует оборот "если . . ., то . . .".
Например, из двух простых высказываний А="На улице светит солнце" и В="На улице
ясная погода" построим сложное, используя оборот-связку "если..., то...".
Получим "Если светит солнце, то на улице ясная погода".
10.
Логическое равенство (Эквивалентность)В естественном языке ему соответствует оборот "... тогда и только тогда, когда ...".
Например, из двух простых высказываний А="На улице ясная погода" и В="На улице
светит солнце" построим сложное, используя оборот-связку "...тогда и только тогда,
когда...".
Получим "На улице ясная погода тогда и только тогда, когда светит солнце".
11.
Примеры высказываний12.
13.
14.
■ Формулы алгебры высказываний будем называть просто формулами. Есть идругие названия для понятия формулы: правильно построенная формула или
правильно построенное выражение, но они представляются менее
предпочтительными. Само определение формулы, носящее индуктивный
характер, на первых порах кажется непривычным. Определения такого типа вам
ранее не встречались. Лучшее понимание этого определения наступит, когда вы
научитесь применять его для определения того, является или не является
формулой последовательность символов (слово), составленная из
пропозициональных переменных, символов логических операций и скобок.
15.
Формулы алгебры высказываний подразделяются на следующие типы: выполнимые,тавтологии, опровержимые и тождественно ложные.
16.
17.
■ Тавтологии представляют собой схемы построения истинных высказываний,независимо от содержания и истинности составляющих высказываний. Так, если
для установления того, истинны или нет высказывания "Саратов основан в 1590
году", "Солнце вращается вокруг Земли", необходимо обладать специальными
знаниями или заглянуть в специальную литературу, то для выяснения значения
истинности высказываний "Треугольник ABC прямоугольный, или треугольник ABC
не прямоугольный", "Неверно, что информация о наследственных признаках
хранится в генах, и эта информация в генах не хранится" уже не нужно обладать
знаниями ни в математике, ни в генетике. Вывод об истинности последних
высказываний делаем, исходя не из их содержания, а из их формы, структуры.
■
Основное значение тавтологий состоит в том, что некоторые из них
предоставляют правильные способы построения умозаключений, т.е. такие
способы, которые от истинных посылок всегда приводят к истинным выводам. А
ведь именно такие рассуждения углубляют наши знания и обогащают их
истинными сведениями. В частности, любая тавтология алгебры высказываний
вида F -> G соответствует некоторой общей схеме логического умозаключения.
18.
Основные тавтологии в математическойлогике
19.
■ В математической теории доказуемые высказывания называются теоремами.Теоремы выводятся из некоторых фиксированных истинных высказываний
(тавтологий), которые называются аксиомами. Подобные математические теории
называют аксиоматическими.
■ В математической логике минимальное множество первичных аксиом, из
которых следуют все тавтологии, называют схемами аксиом. Логика
высказываний является аксиоматической теорией исчисления высказываний.
Теоремами этой теории являются тавтологии.
■ Известны различные схемы аксиом [13, 14], например, схемы аксиом Гильберта
и Аккермана:
20.
■ Формальное доказательство (схема вывода) – последовательность формул,каждая из которых:
- аксиома;
- получена подстановкой формул в аксиому;
- результат применения правила МР.
■ Все формулы в последовательности – тавтологии и последняя формула в этой
последовательности - логическое следствие или теорема.
■ Из схемы аксиом выводятся только тавтологии, которые обозначаются
-> В
■ Вывод - доказательство теорем – нетривиальная задача, требующая
изобретательности и интуиции.
■ Вывод альтернатива алгебраическому доказательству и доказано, что он всегда
существует.
21.
Пример вывода теоремы из аксиом22.
■ Гипотезы – истинные по определению, убеждению или опыту утверждения внекоторой области. В отличие от аксиом теории высказываний гипотезы Г не
обязательно тавтологии, но непротиворечивы.
■ В отличие от вывода в аксиоматической теории, вывод формулы В из гипотез (Г L
B) подтверждает не общезначимость формулы В, а только ее истинность при
интерпретациях, в которых истинны гипотезы Г. Формула В вне этой области
истинности конкретных гипотез может быть ложной.
■ Следовательно, правильные рассуждения имеют смысл только в данной
конкретной области знаний. Причем тавтология не может быть получена при
выводе из гипотез, которые не являются тавтологиями - что следует из полноты и
непротиворечивости теории исчисления высказываний.
23.
24.
Методы доказательств теорем25.
26.
Математическая индукцияДокажем следующее утверждение: Если мы суммируем нечетные
натуральные числа то сумма такого ряда будет n^2

























 Математика
Математика








