Физика колебаний и волн. Квантовая физика. Лекция №1

1. Физика колебаний и волн. Квантовая физика.

2. Лекция № 1

1. Общие представления о волновых
процессах. Волновое движение.
2. Фазовая скорость и фронт волны.
3. Плоские и сферические волны.
4. Скалярное волновое уравнение.

3.

Виды и признаки колебаний
В физике особенно выделяют колебания двух
видов – механические и электромагнитные и их
электромеханические комбинации, поскольку они
чрезвычайно актуальны для жизнедеятельности
человека.
Для колебаний характерно превращение одного
вида энергии в другую – кинетической в
потенциальную, магнитной в электрическую и т.д.
Колебательным движением (или просто
колебанием)
называются
процессы,
повторяющиеся во времени.
Существуют общие закономерности этих
явлений.

4.

При распространении волны, частицы среды не
движутся вместе с волной, а колеблются около своих
положений равновесия.
Вместе с волной от частицы к частице, передается
лишь состояние колебательного движения и его энергия.
Поэтому основным свойством всех волн независимо от их
природы является перенос энергии без переноса вещества.

5.

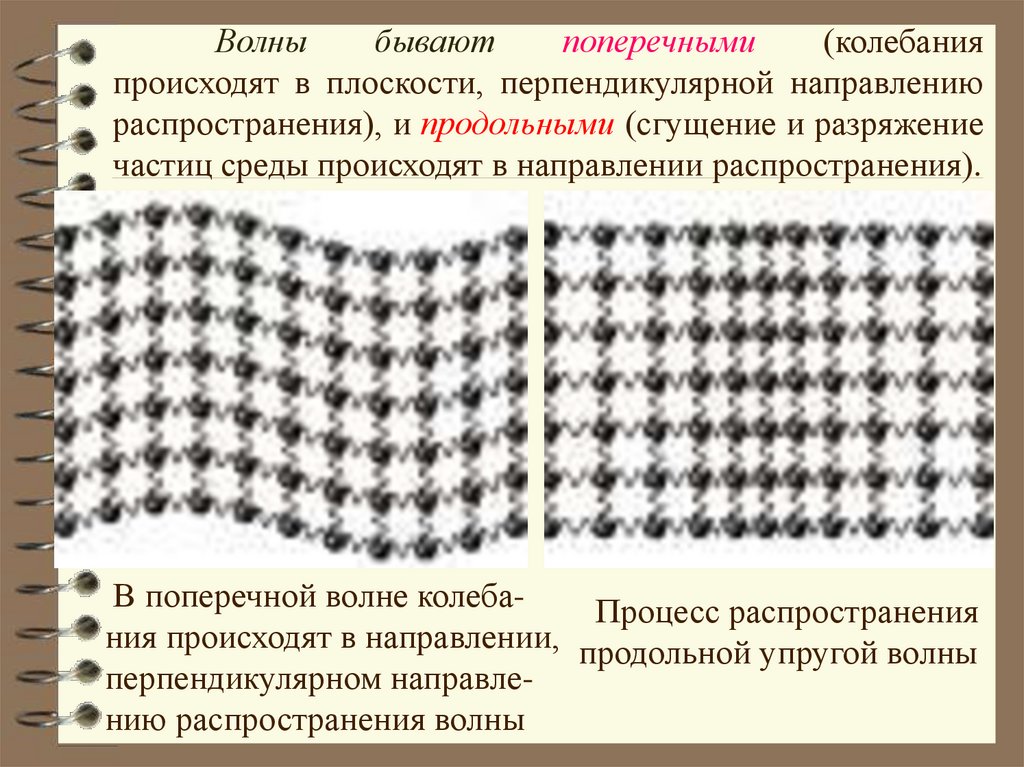
Волны
бывают
поперечными
(колебания
происходят в плоскости, перпендикулярной направлению
распространения), и продольными (сгущение и разряжение
частиц среды происходят в направлении распространения).
В поперечной волне колебаПроцесс распространения
ния происходят в направлении, продольной упругой волны
перпендикулярном направлению распространения волны

6.

Движение молекул в волне на поверхности
жидкости
У поверхностных волн взаимосвязь между
соседними молекулами при передаче колебаний
осуществляется не силами упругости, а силами
поверхностного натяжения и тяжести. В случае малой
амплитуды волны каждая молекула движется по
окружности, радиус которой убывает с расстоянием от
поверхности. Нижние молекулы находятся в покое.

7.

Волна на поверхности жидкости –
суперпозиция продольного и поперечного
движения молекул

8.

Наложение продольной и поперечной волн равной
амплитуды, сдвинутых по фазе на π/2.
В результате каждая масса совершает круговые
движения.

9.

Волновая функция-это
ξ ξ( x, y, z, t )
смещение точек из положения равновесия.
Расстояние между ближайшими частицами, колеблющимися
в одинаковой фазе, называется длиной волны :
1
T
ν
λ υT
– период,
– частота.
υ λν – скорость распространения волны.
В среде без дисперсии скорость распространения
волны
есть фазовая скорость или скорость
распространения поверхности постоянной фазы.
υ

10.

Фазовая скорость
– это скорость распространения фазы волны.
dx
υ
dt
– скорость распространения фазы есть
скорость распространения волны.
Для синусоидальной волны скорость переноса
энергии равна фазовой скорости.
10

11.

Фронт волны – геометрическое место точек, до
которых доходит возмущение в момент времени t :
это та поверхность, которая отделяет часть
пространства, уже вовлеченную в волновой процесс, от
области, в которой колебания еще не возникли.
(В однородной среде направление распространения
перпендикулярно фронту волны )
Волновая (фазовая) поверхность – геометрическое место
точек, колеблющихся в одинаковой
фазе.
Число волновых поверхностей –
бесконечно.
Фронт волны – один.
Волновые поверхности
неподвижны,
Фронт волны все время переме-

12.

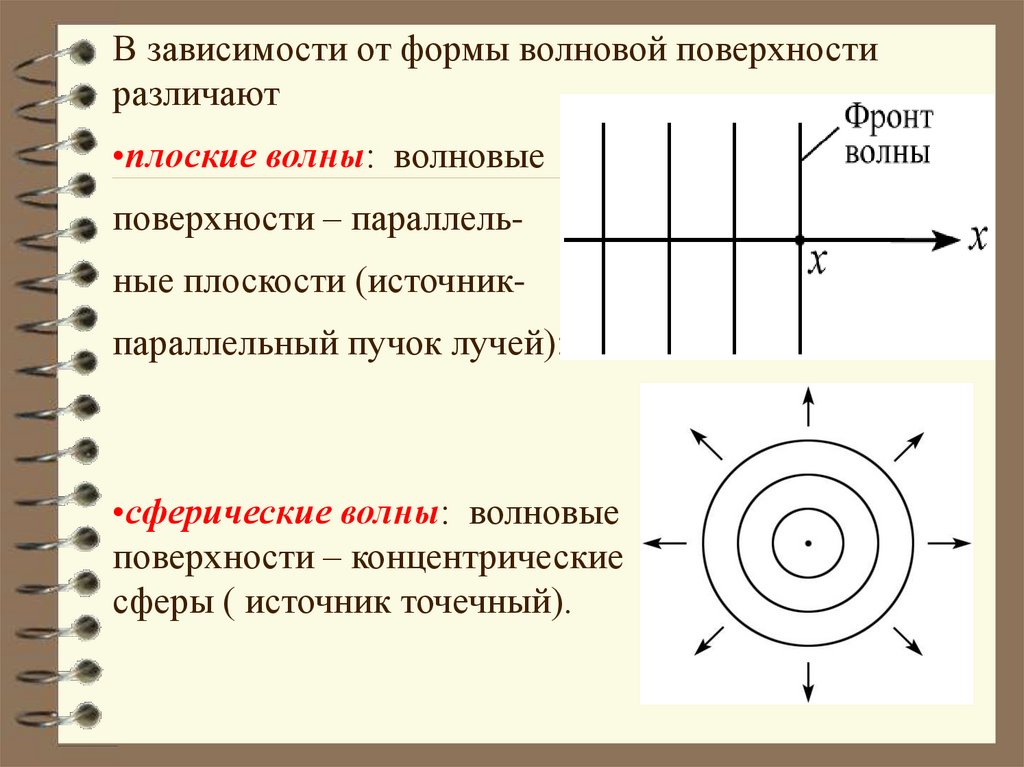
В зависимости от формы волновой поверхности
различают
•плоские волны: волновые
поверхности – параллельные плоскости (источникпараллельный пучок лучей):
•сферические волны: волновые
поверхности – концентрические
сферы ( источник точечный).

13.

Уравнение плоской волны
Найдем вид волновой функции, в случае плоской
волны предполагая, что колебания источника носят
гармонический характер:
A cos( t 0 )
Пусть
φ0 0
ξ ξ(0, t ) A cosωt
x
Чтобы пройти волне путь x нужно время: τ
υ
x
ξ ( x, t ) A cosω t
υ
– это уравнение плоской волны
(смещение частиц в волне).

14.

Введем волновое число
2π
k
λ
2π
или в векторной форме волновой вектор: k
n
λ
2
π
2
πν
ω
Длина волны: λ υT , то k
υT
υ
υ
ω
Фазовая скорость: υ
k
Тогда уравнение плоской волны запишется:
ξ A cos(ωt kx)
Скорость смещения частиц в упругой волне будет:
d
ux
A sin( t kx)
dt

15.

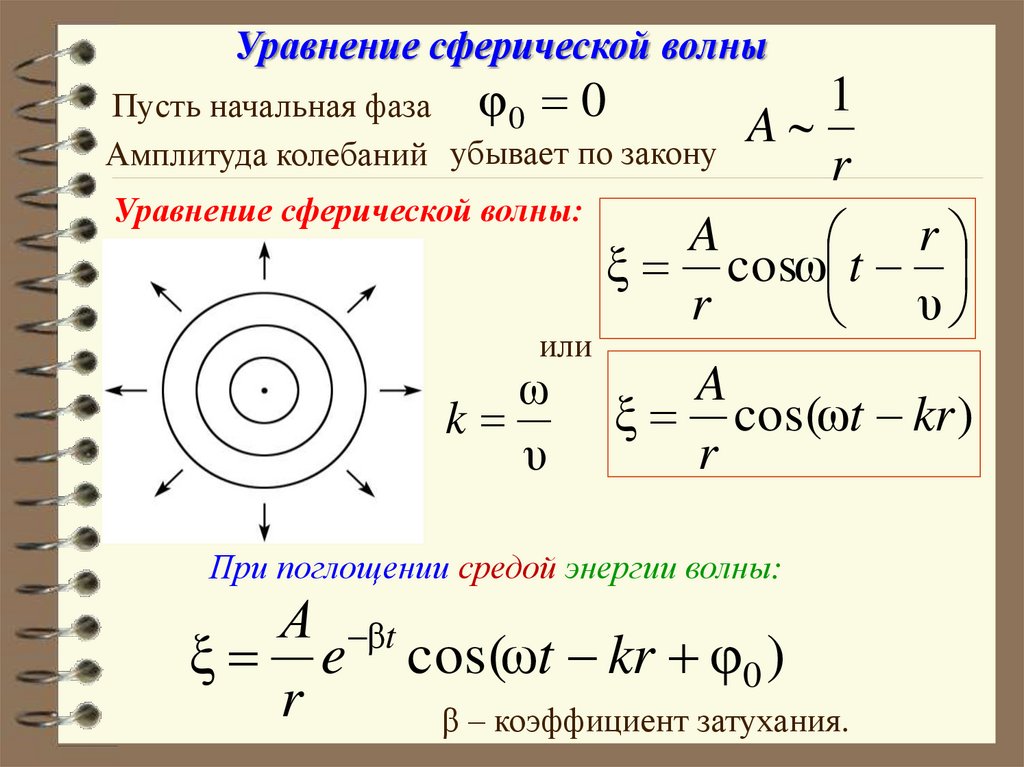
Уравнение сферической волны
Пусть начальная фаза φ 0 0
Амплитуда колебаний убывает по закону
1
A
r
Уравнение сферической волны:
A
r
ξ cosω t
r
υ
или
A
ω
ξ cos(ωt kr )
k
r
υ
При поглощении средой энергии волны:
А βt
ξ e cos(ωt kr φ0 )
r
β – коэффициент затухания.

16.

Волновое уравнение
Распространение волн в однородной среде в
общем случае описывается волновым уравнением –
дифференциальным уравнением в частных
производных (скалярное волновое уравнение):
1
2 2 2 2 0
2
x
y
z t
2
или
2
2
2
2
1
2
2 2 0
t
Всякая функция, удовлетворяющая этому
уравнению, описывает некоторую волну, причем
υ -фазовая скорость волны.

17.

Решением волнового уравнения
2
1
2
2 2 0
t
является уравнение любой волны, например:
сферической:
A
ξ cos(ωt kr )
r
или плоской :
A cos( t kr)
Для плоской волны, распространяющейся
вдоль оси x, волновое уравнение упрощается:
1
2 2 0
2
x t
2
2
2
2
2
где 2 2 2 2
x y z
- оператор Лапласа.

18.

ЛЕКЦИЯ ЗАКОНЧЕНА!