Сезонная декомпозиция и рекуррентное прогнозирование стационарных временных рядов. Лекция 4 (часть 1)

1. Лекция 4 (часть первая)

Сезонная декомпозиция и
рекуррентное
прогнозирование
стационарных временных
рядов

2. Реализуемые компетенции

ОПК-1 готовностью к самостоятельной работе
ОПК-2 способностью использовать современные математические методы и
современные прикладные программные средства и осваивать современные технологии
программирования
ПК-1 способностью использовать стандартные пакеты прикладных программ для
решения практических задач на электронных вычислительных машинах, отлаживать,
тестировать прикладное программное обеспечение
ПК-9 способностью выявить естественнонаучную сущность проблем, возникающих в
ходе профессиональной деятельности, готовностью использовать для их решения
соответствующий естественнонаучный аппарат
ПК-10 готовностью применять математический аппарат для решения поставленных
задач, способностью применить соответствующую процессу математическую модель и
проверить ее адекватность, провести анализ результатов моделирования, принять
решение на основе полученных результатов
ПК-11 готовностью применять знания и навыки управления информацией
ПК-12 способностью самостоятельно изучать новые разделы фундаментальных наук
2

3. Цель лекции

Цель лекции - формирование теоретических
знаний о моделях стационарных одномерных
временных рядов, позволяющих прогнозировать
социально-экономические явления и процессы на
краткосрочную
перспективу,
а
также
формирование навыков реализации указанных
моделей и методов в пакетах прикладных
программ
3

4. План лекции

1. Метод
постоянной
средней
сезонной
декомпозиции стационарных временных
рядов
2. Понятие экспоненциальной средней
3. Математическое ожидание и дисперсия
сглаженного ряда
4. Выбор значения параметра адаптации
5. Выбор начальных условий сглаживания
4

5. График стационарного ряда с сезонностью (без тренда и с аддитивной сезонностью)

3,5
3
2,5
2
1,5
1
0,5
0
1
4
7
10 13 16 19 22 25 28 31 34 37 40 43 46
5

6. Метод постоянной средней

Метод постоянной средней применяется для расчета сезонных
индексов при отсутствии тенденции во временном ряду, то есть для рядов,
уровни которых можно представить как:
t vt t
Данный метод используется только при аддитивной сезонности. На
первом этапе рассчитывается значение выборочной средней y . На втором
этапе находят отношения между уровнями временного ряда и значением
выборочной средней:
xt
yt
y
(1)
6

7. Метод постоянной средней

На третьем этапе рассчитывают показатели (индексы) сезонности как
среднее для одноименных периодов j, j=1,…,k; k=4 для квартальных данных,
k=12 для помесячных данных. Другими словами временной ряд длиной
N=m*k, где m-число лет.
Тогда сезонный индекс для j-ого сезона
m
vˆ j
x
i 0
j ik
m
,
(2)
j=1,…,k
Прогнозное значение для временного ряда:
yˆ N L у * vˆ j ,
(3)
где N+L соответствует периоду j.
7

8. Пример метода постоянной средней

Имеются данные по объему продаж газированных напитков магазина
за период с января 2009 по март 2014 года. Исследование показало
отсутствие тренда в ряду динамики и наличие сезонности, а среднегодовой
объем продаж напитков составил 400 тыс.руб. Оценки показателей
сезонности представлены в таблице.
Таблица 1 – Индексы сезонности
№ месяца, 1
j
Сезонный 0,5
индекс, vj
2
3
4
5
0,4
0,6 0,8 1,0
6
7
8
9
10
11
12
1,4
2,1
2,2
1,2
0,8
0,4
0,6
Найдем прогноз на апрель- июнь 2014 года.
8

9. Пример метода постоянной средней

Решение.
Длина
временного
ряда
N=5*12+3=63.
Прогноз
осуществляется на периоды 64,65,66 с номерами месяцев (j) 4,5,6.
yˆ 64 400 * v4 400 * 0,8 320 тыс.руб.
yˆ 65 400 * v5 400 *1 400 тыс.руб.
yˆ 66 400 * v6 400 *1,4 560 тыс.руб.
Домашнее задание. Записать алгоритм метода постоянной средней с
использованием сезонных показателей.
9

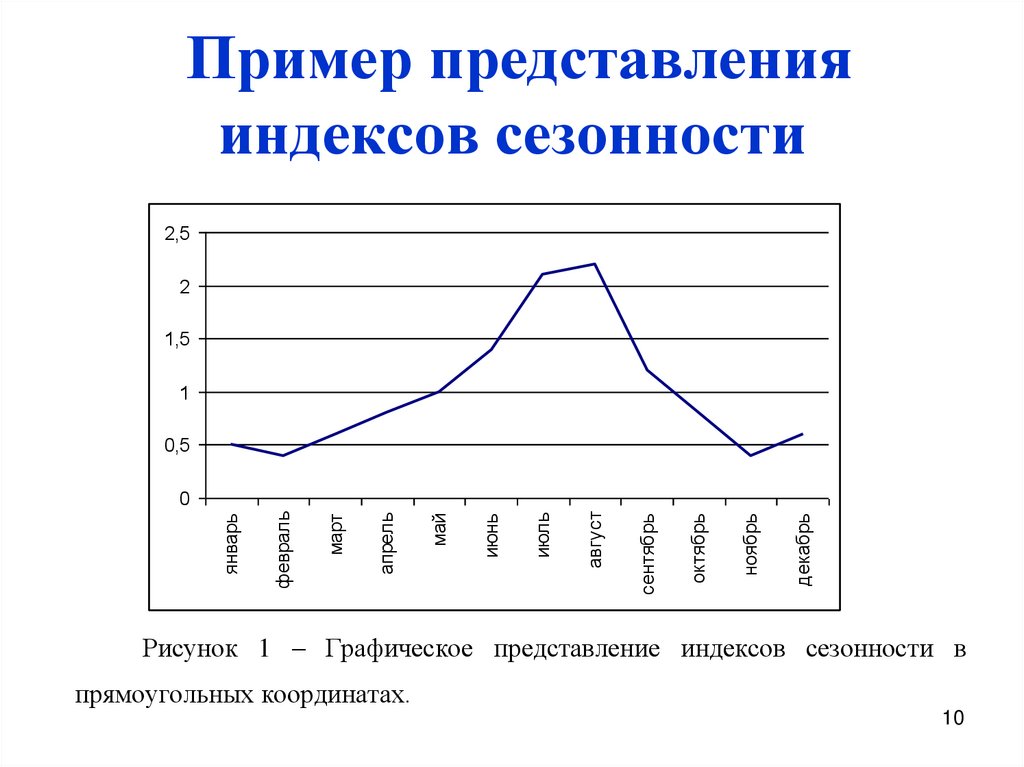
10. Пример представления индексов сезонности

2,5
2
1,5
1
0,5
декабрь
ноябрь
октябрь
сентябрь
август
июль
июнь
май
апрель
март
февраль
январь
0
Рисунок 1 – Графическое представление индексов сезонности в
прямоугольных координатах.
10

11. Пример представления индексов сезонности

декабрь
январь
2,5
2
февраль
1,5
ноябрь
март
1
0,5
октябрь
0
апрель
сентябрь
май
август
июнь
июль
Рисунок
2
-
Изображение
индексов
сезонности
в
полярных
координатах
11

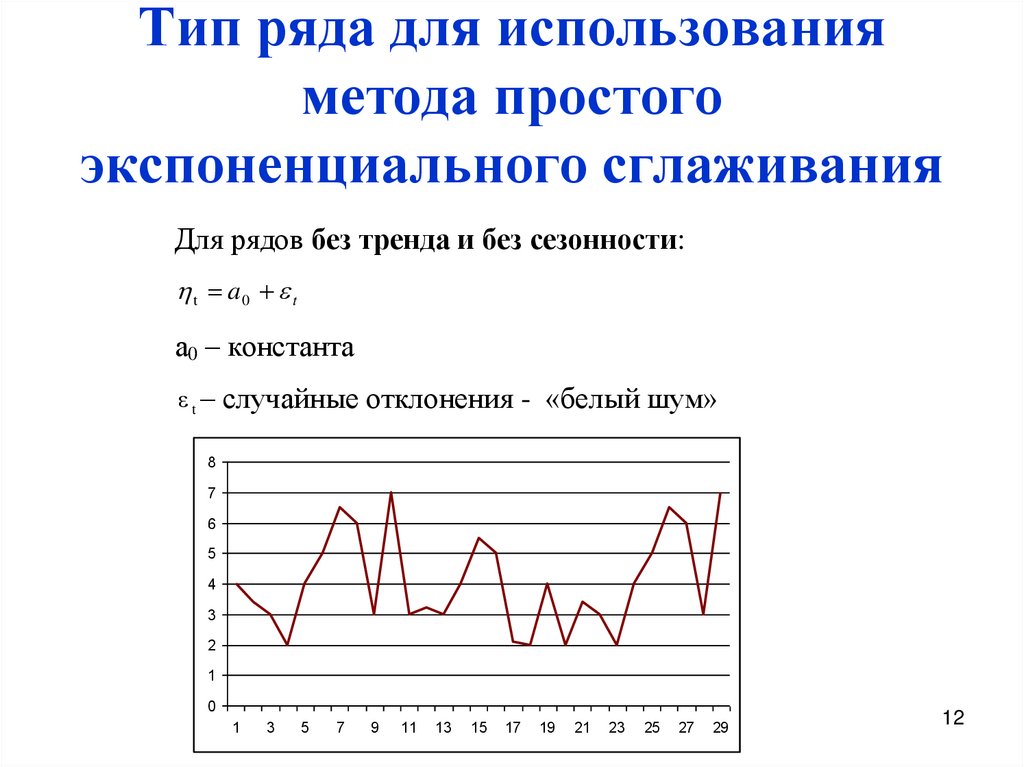
12. Тип ряда для использования метода простого экспоненциального сглаживания

Для рядов без тренда и без сезонности:
t a0 t
а0 – константа
t – случайные отклонения - «белый шум»
8
7
6
5
4
3
2
1
0
1
3
5
7
9
11
13
15
17
19
21
23
25
27
29
12

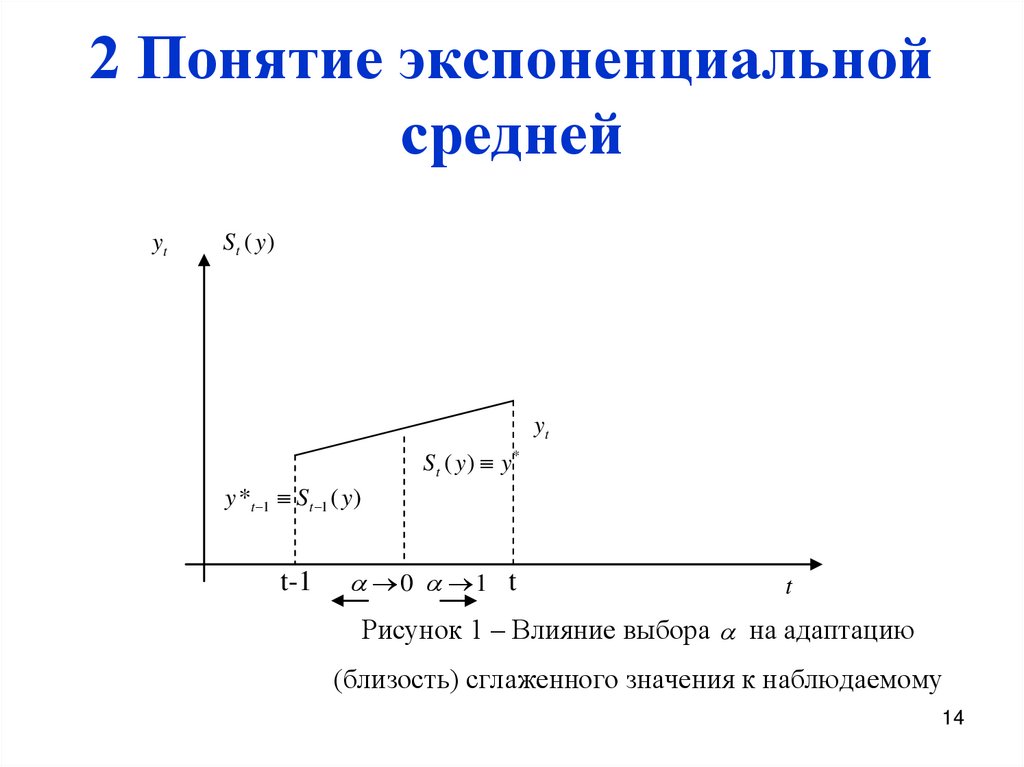
13. 2 Понятие экспоненциальной средней

Сущность метода заключается в последовательном использовании
вычислительного алгоритма:
S t ( y) y t (1 )S t 1 ( y) = y t St 1 ( у)
(4)
где S t - значение экспоненциальной средней;
- параметр сглаживания (адаптации), 0< <1. На рисунке 1
продемонстрирована суть экспоненциального сглаживания при разных
;
- параметр затухания.
13

14. 2 Понятие экспоненциальной средней

yt
St ( y)
yt
St ( y) y *
y *t 1 St 1 ( y)
t-1
0 1 t
t
Рисунок 1 – Влияние выбора на адаптацию
(близость) сглаженного значения к наблюдаемому
14

15. 2 Понятие экспоненциальной средней

Распишем (4) в виде:
St ( y) y t (1 )St 1 ( y) (1а)
St -1 ( y) y t 1 (1 )St 2 ( y) (1б)
St -2 ( y) y t 2 (1 )St 3 ( y) (1в)
St ( y) yt (1 )St 1 ( y) yt yt 1 2St 2 ( y)
yt yt 1 2 yt 2 3St 3 ( y) ...
(5)
15

16. 2 Понятие экспоненциальной средней

Тогда:
t
St ( y ) i y t i
(5а)
i 0
Таким образом, величина St ( у) - представляет собой взвешенную
сумму всех членов ряда с весами i , где i возрастает по мере старения
информации, другими словами отдельных уровней ряда убывают по
мере их удаления в прошлое в соответствии с показательной
закономерностью (в зависимости от возраста наблюдений).
16

17. 3 Математическое ожидание и дисперсия сглаженного ряда

Пусть рассматривается ряд динамики вида:
t a0 t
а0 – константа
t – случайные отклонения - «белый шум», то есть
M ( t ) 0;
D( t ) const 2 ;
cov( t t ) 0, 0.
17

18. 3 Математическое ожидание и дисперсия сглаженного ряда

Применим процедуру экспоненциального сглаживания.
t
t
S t ( y ) yt i i (a0 t i ) a0
i
i 0
i 0
i
1
(1 )i геом.прогр.
i t i
(6)
t
a 0 i t i
i 0
18

19. 3 Математическое ожидание и дисперсия сглаженного ряда

M St ( y) М( a 0 i t i ) а 0
t
то есть математическое ожидание
i 0
сглаженного ряда равно математическому ожиданию исходного ряда
динамики. Найдем дисперсию сглаженного ряда:
t
D(St ( y)) M(St a 0 ) M (a0 i t i a0 ) 2
2
i 0
2 2
2 2
M( t i )
2.
2
1 1 2
1
i 0
i 0
t
t
i
2
2
2i
2
(7)
2
Таким образом, сглаженный ряд имеет то же математическое ожидание, что
и исходный ряд, но меньшую дисперсию – уменьшение дисперсии в
2
раза.
19

20. 4 Выбор значения параметра адаптации

Если стремится к 1 – это означает, что при прогнозе в основном
учитывается влияние только последних уровней временного ряда.
Если стремится к 0 – это означает, что при прогнозе учитывается
влияние прошлых уровней временного ряда.
Если =0 – отсутствие адаптации, полная фильтрация.
Если =1 – «наивная» модель, согласно которой прогноз в каждый
момент времени равен начальному уровню.
20

21. 4 Выбор значения параметра адаптации

Однозначного
параметра
критерия
сглаживания
выбора
компромиссного
значения
нет.
Автор
простого
метода
экспоненциального сглаживания Р.Г. Браун предложил следующую
формулу расчета .
=2/(N+1)
(8)
где N - число уровней временного ряда, вошедших в интервал
сглаживания.
В литературе иногда рекомендуется брать в пределах от 0,1 до
0,3 по умолчанию. Однако, наилучшее значения в общем случае
должно зависеть от срока прогнозирования.
21

22. 4 Выбор значения параметра адаптации

Возраст текущего наблюдения
равен
0, возраст предыдущего
наблюдения равен 1 и т.д. Средний возраст – это сумма взвешенных
возрастов данных, использованных для подсчета сглаженной величины.
Причем возраста имеют те же веса, что и соответствующая информация.
Средний возраст информации равен:
k 0 1 2 ... i i i i 1 (признаки сходимости рядов )
2
i 1
1
1
i
i 0
1
(9)
Таким образом, чем меньше , тем больше средний возраст
информации. Для конъюнктурных прогнозов значение , как правило, надо
брать большим, а для более долгосрочных – малым.
22

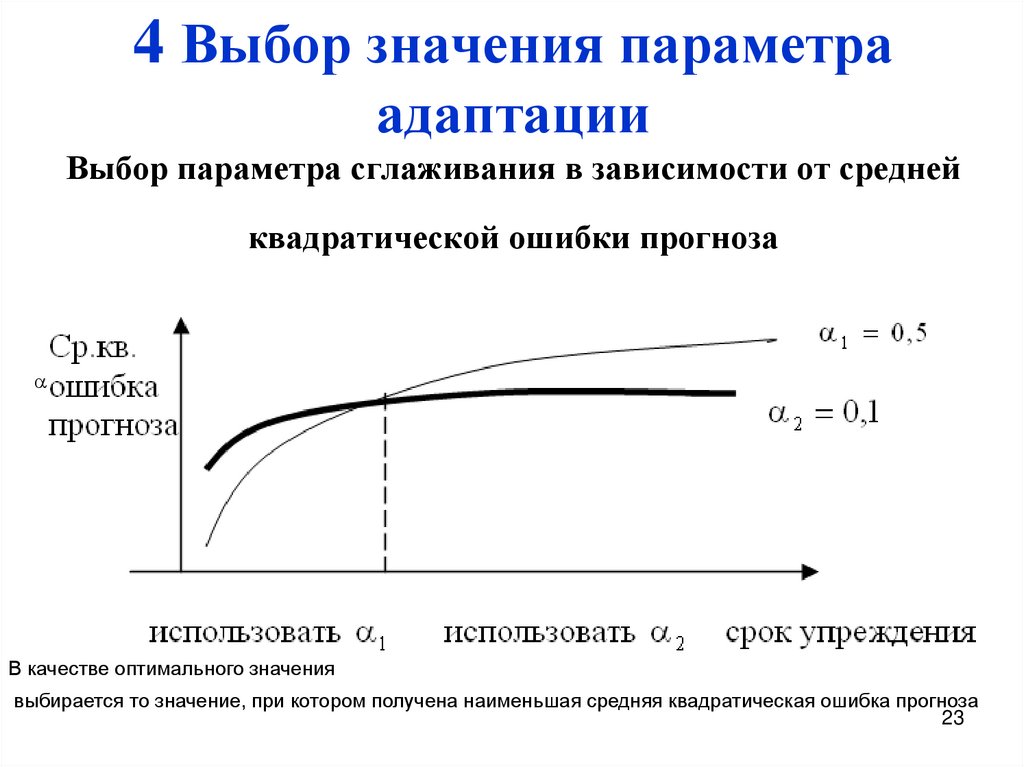
23. 4 Выбор значения параметра адаптации Выбор параметра сглаживания в зависимости от средней квадратической ошибки прогноза

В качестве оптимального значения
выбирается то значение, при котором получена наименьшая средняя квадратическая ошибка прогноза
23

24. 5 Выбор начальных условий сглаживания

Прежде чем приступать к определению экспоненциальных средних,
необходимо, кроме параметра определить St -1 ( y) (при t=1 необходимо
определить S0 ( y) ), то есть возникает проблема определения начальных
условий.
S1 ( y) y1 (1 )S0 ( y)
Таким
образом,
прогнозирование
методом
простого
экспоненциального сглаживания может быть реализовано в двух возможных
вариантах:
- начальные условия известны;
- начальные условия неизвестны.
24

25. 5 Выбор начальных условий сглаживания

Начальные условия известны. Возможны два случая реализации
этого варианта:
- в качестве начального условия S0 может быть использована средняя
арифметическая, определенная по всем значениям уровней исходного
временного ряда. Использование средней арифметической возможно, если
есть данные о развитии изучаемого социально-экономического явления в
прошлом.
- в качестве начального условия возможно использование первого
уровня исходного временного ряда. При этом вес данного уровня будет
уменьшаться по мере скольжения по уровням исходного временного ряда от
уровня к уровню, а, следовательно, будет уменьшаться влияние каждого
следующего уровня на величину экспоненциальной средней.
25

26. 5 Выбор начальных условий сглаживания

Начальные условия неизвестны. Они могут быть определены по
формулам, разработанным Брауном (см. Учебник Лукашин. Адаптивные
методы краткосрочного прогнозирования).
Прогнозная модель имеет вид:
x̂ (t ) â 0, t
Средством
экспоненциальная
оценки
единственного
средняя
â 0, t S t .
параметра
Таким
модели
образом,
служит
свойства
экспоненциальной средней распространяются на прогнозную модель. В
частности если S t -1 ( y) рассматривать как прогноз на 1 шаг вперед, то
разность yt и S t -1 ( y) есть погрешность этого прогноза, а новый прогноз
получается в результате корректировки предыдущего прогноза с учетом его
ошибки.
26

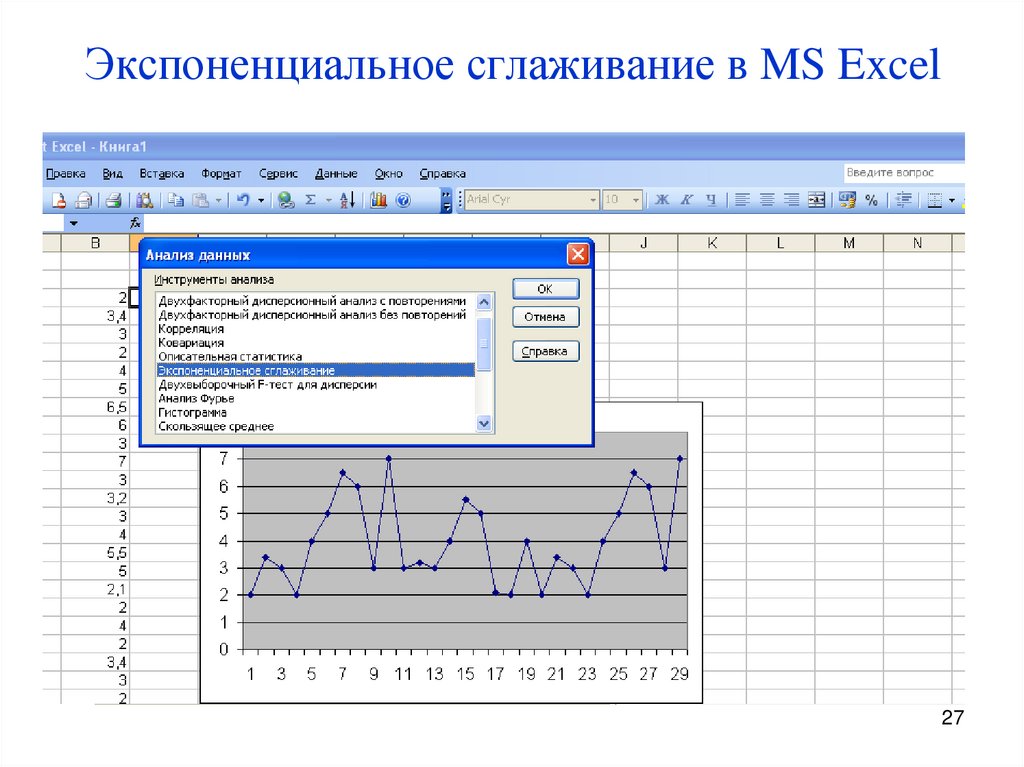
27. Экспоненциальное сглаживание в MS Excel

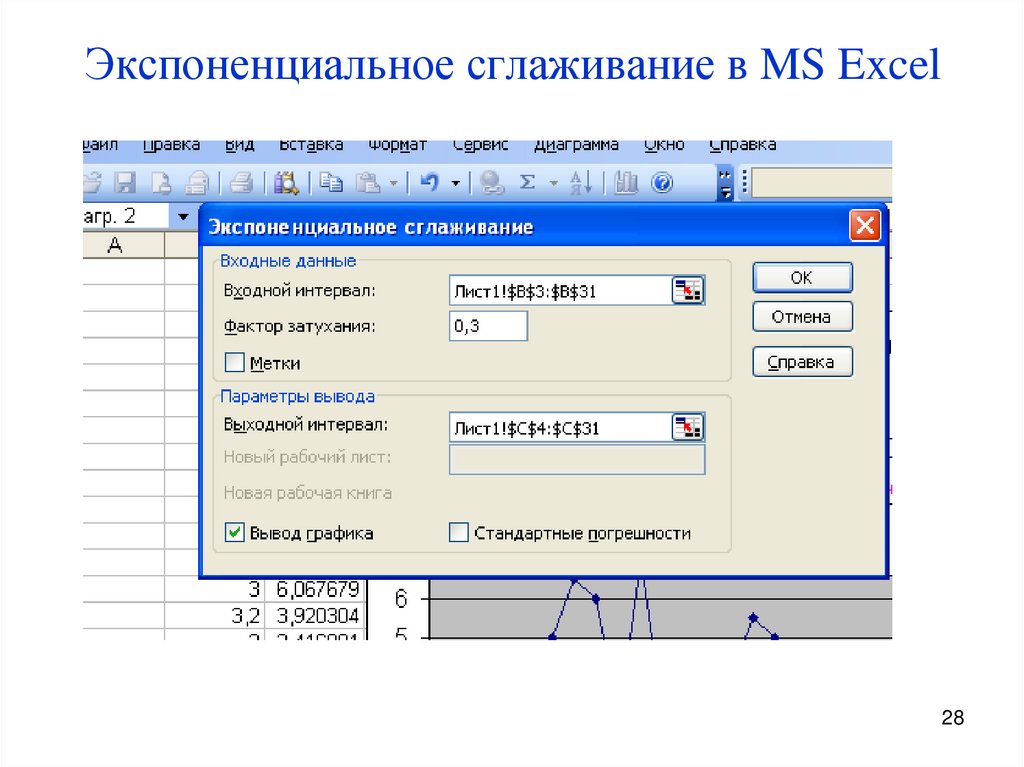
27

28. Экспоненциальное сглаживание в MS Excel

28

29. Экспоненциальное сглаживание в MS Excel

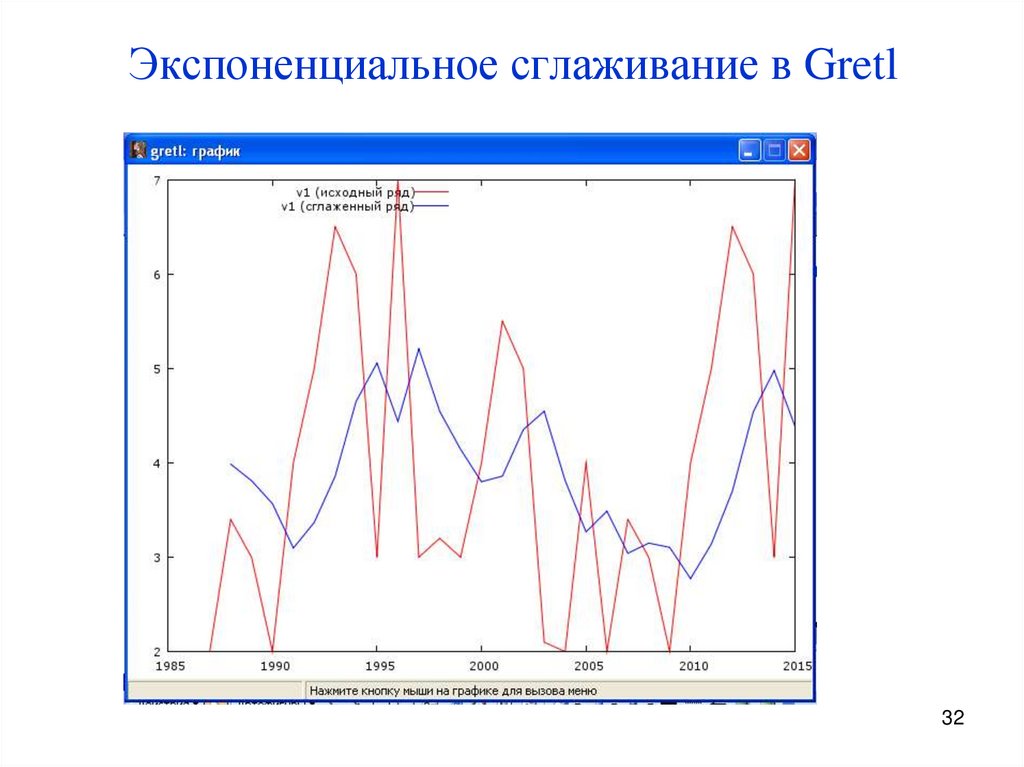
29

30. Экспоненциальное сглаживание в Gretl

30

31. Экспоненциальное сглаживание в Gretl

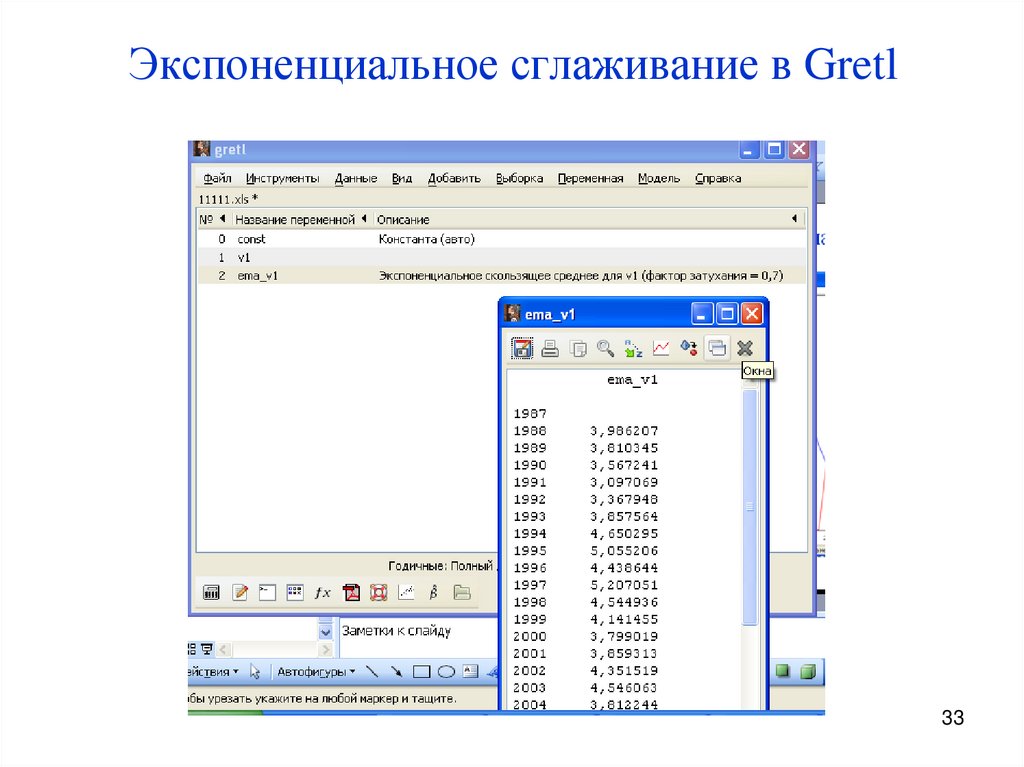
31

32. Экспоненциальное сглаживание в Gretl

32

33. Экспоненциальное сглаживание в Gretl

33

34. Задание на практическое занятие

1. Опрос по лекции
2. Рассчитать во сколько раз уменьшится
дисперсия сглаженного ряда для значения
параметра адаптации 0,25; 0,5; 0,8; 0,9.
3. Найти средний возраст данных при
параметре затухания равным 0,7; 0,2; 0,9.
34

35. Литература к лекции

1. Дуброва, Т. А. Статистические методы
прогнозирования[Текст] : учебное
пособие / Т. А. Дуброва. - Москва :
ЮНИТИ-ДАНА, 2003. - 206 с.
2. Лукашин, Ю. П. Адаптивные методы
краткосрочного прогнозирования
временных рядов [Текст] : учеб. пособие
для вузов / Ю. П. Лукашин. - М. :
Финансы и статистика, 2003. - 416 с.
35