Похожие презентации:
Параллельные плоскости
1.
2.
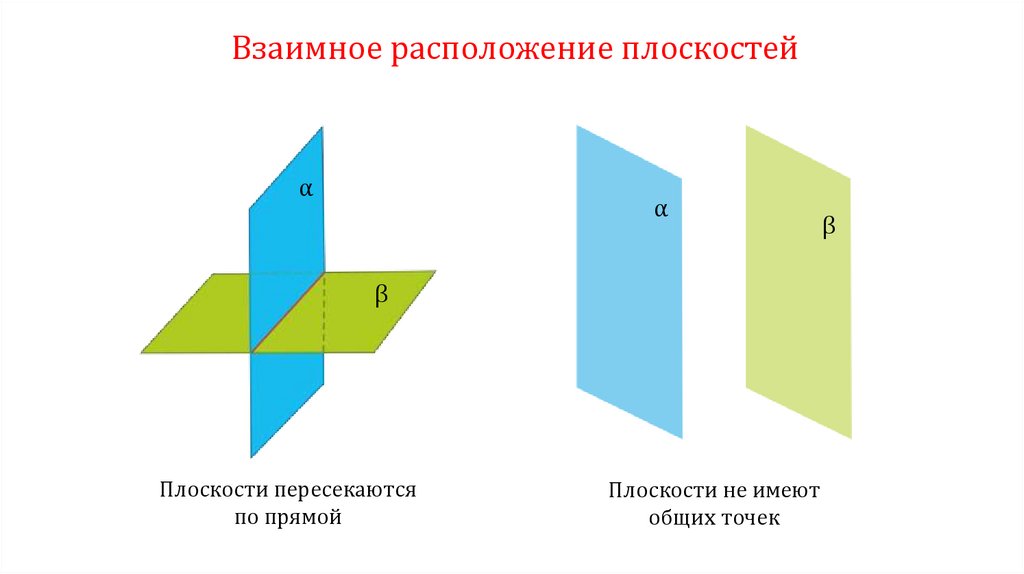
Взаимное расположение плоскостейα
α
β
Плоскости пересекаются
по прямой
Плоскости не имеют
общих точек
β
3.
ОпределениеДве плоскости называются параллельными, если они
не пересекаются
α
β
α∥β
4.
Теорема(признак параллельности плоскостей)
Если две пересекающиеся прямые одной
плоскости соответственно параллельны
двум пересекающимся прямым другой
плоскости, то эти плоскости параллельны
5.
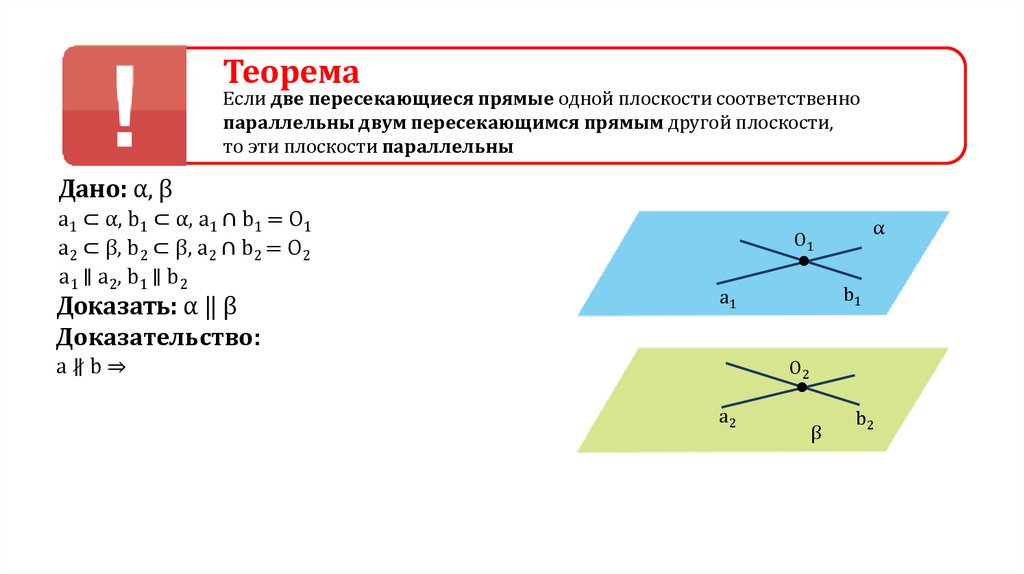
ТеоремаЕсли две пересекающиеся прямые одной плоскости соответственно
параллельны двум пересекающимся прямым другой плоскости,
то эти плоскости параллельны
Дано: α, β
a1 ⊂ α, b1 ⊂ α, a1 ∩ b1 = O1
a2 ⊂ β, b2 ⊂ β, a2 ∩ b2 = O2
a1 ∥ a2, b1 ∥ b2
Доказать: α ‖ β
α
O1
b1
a1
O2
a2
β
b2
6.
ТеоремаЕсли две пересекающиеся прямые одной плоскости соответственно
параллельны двум пересекающимся прямым другой плоскости,
то эти плоскости параллельны
Дано: α, β
a1 ⊂ α, b1 ⊂ α, a1 ∩ b1 = O1
a2 ⊂ β, b2 ⊂ β, a2 ∩ b2 = O2
a1 ∥ a2, b1 ∥ b2
Доказать: α ‖ β
Доказательство:
α
O1
b1
a1
a∦b⇒
O2
a2
β
b2
7.
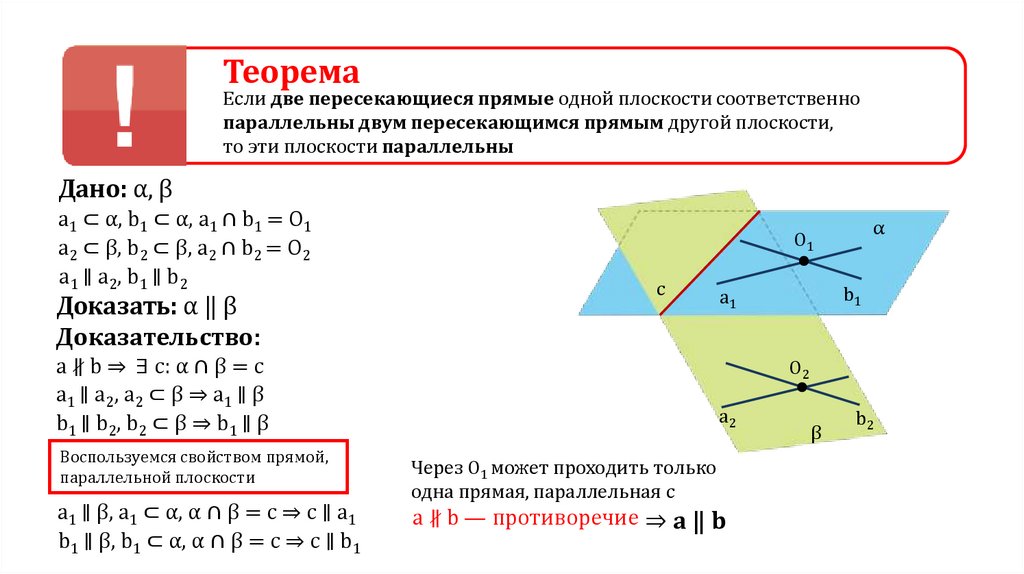
ТеоремаЕсли две пересекающиеся прямые одной плоскости соответственно
параллельны двум пересекающимся прямым другой плоскости,
то эти плоскости параллельны
Дано: α, β
a1 ⊂ α, b1 ⊂ α, a1 ∩ b1 = O1
a2 ⊂ β, b2 ⊂ β, a2 ∩ b2 = O2
a1 ∥ a2, b1 ∥ b2
Доказать: α ‖ β
Доказательство:
c
a ∦ b ⇒ ∃ c: α ∩ β = c
a1 ∥ a2, a2 ⊂ β ⇒ a1 ∥ β
b1 ∥ b2, b2 ⊂ β ⇒ b1 ∥ β
Воспользуемся свойством прямой,
параллельной плоскости
a1 ∥ β, a1 ⊂ α, α ∩ β = c ⇒ c ∥ a1
b1 ∥ β, b1 ⊂ α, α ∩ β = c ⇒ c ∥ b1
α
O1
b1
a1
O2
a2
Через O1 может проходить только
одна прямая, параллельная с
a ∦ b — противоречие ⇒ a ‖ b
β
b2
8.
ТеоремаЕсли две пересекающиеся прямые одной плоскости соответственно
параллельны двум пересекающимся прямым другой плоскости,
то эти плоскости параллельны
Дано: α, β
a1 ⊂ α, b1 ⊂ α, a1 ∩ b1 = O1
a2 ⊂ β, b2 ⊂ β, a2 ∩ b2 = O2
a1 ∥ a2, b1 ∥ b2
a ∦ b ⇒ ∃ c: α ∩ β = c
a1 ∥ a2, a2 ⊂ β ⇒ a1 ∥ β
b1 ∥ b2, b2 ⊂ β ⇒ b1 ∥ β
a1 ∥ β, a1 ⊂ α, α ∩ β = c ⇒ c ∥ a1
b1 ∥ β, b1 ⊂ α, α ∩ β = c ⇒ c ∥ b1
b1
a1
Доказать: α ‖ β
Доказательство:
Воспользуемся свойством прямой,
параллельной плоскости
α
O1
O2
a2
β
b2
Через O1 может проходить только
одна прямая, параллельная с
a ∦ b — противоречие ⇒ a ‖ b
Теорема доказана
9.
Задача 1Дано: A1A2, B1B2 и C1C2 не лежат
в одной плоскости
O — общая середина
C1
A1
B2
O
Доказать:
(A1B1C1) ∥ (A2B2C2)
Доказательство:
A1B1 ∩ A1C1 = A1, A2B2 ∩ A2C2 = A2
A2
B1
C2
⇒ A1B1 ∥ A2B2
Аналогично из A1C1A2C2: A1C1 ∥ A2C2
(A1B1C1) ∥ (A2B2C2)
По признаку параллельности
плоскостей
Что и требовалось доказать
10.
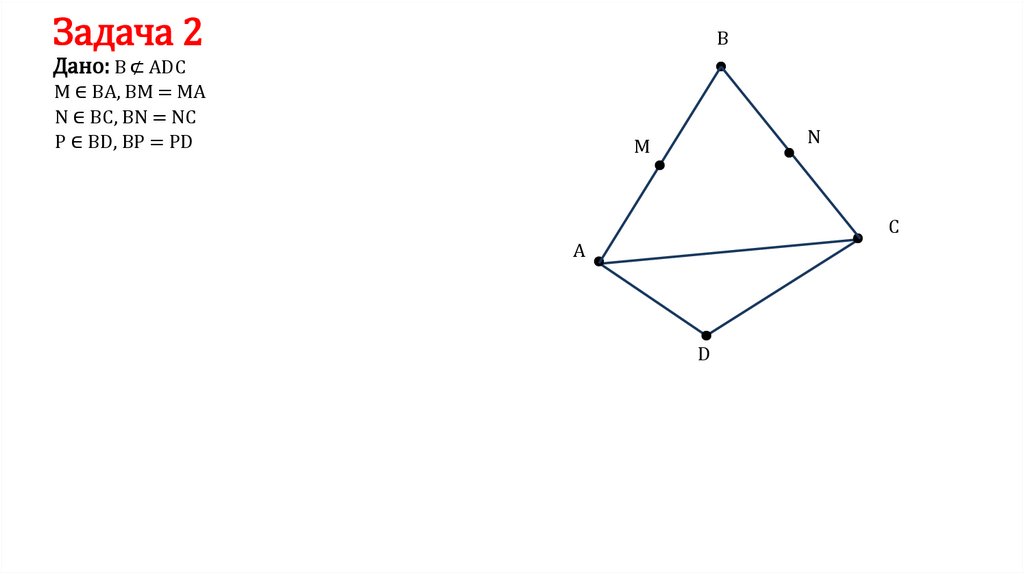
Задача 2B
Дано: B ⊄ ADC
M ∈ BA, BM = MA
N ∈ BC, BN = NC
P ∈ BD, BP = PD
N
M
C
A
D
11.
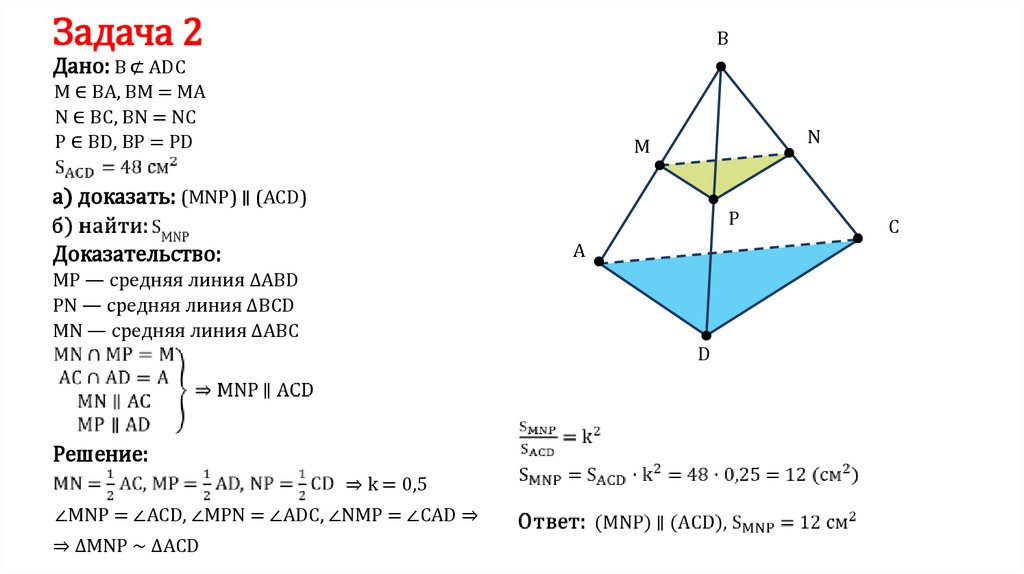
Задача 2B
Дано: B ⊄ ADC
M ∈ BA, BM = MA
N ∈ BC, BN = NC
P ∈ BD, BP = PD
N
M
а) доказать: (MNP) ∥ (ACD)
P
A
Доказательство:
MP — средняя линия ∆ABD
PN — средняя линия ∆BCD
MN — средняя линия ∆ABC
D
Решение:
⇒ k = 0,5
∠MNP = ∠ACD, ∠MPN = ∠ADC, ∠NMP = ∠CAD ⇒
⇒ ∆MNP ∼ ∆ACD
C






 Математика
Математика








