Параллельность плоскостей

1.

2.

Согласно аксиоме A3, если две
плоскости имеют общую точку, то они
пересекаются по прямой.
Отсюда следует, что плоскости либо
пересекаются по прямой, либо не
пересекаются, т. е. не имеют ни одной
общей точку.

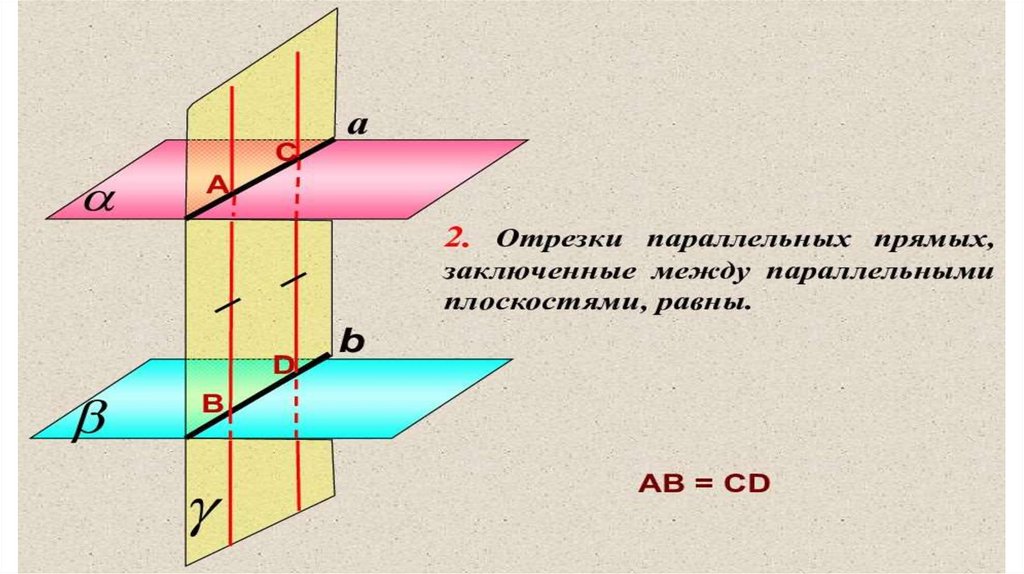
3.

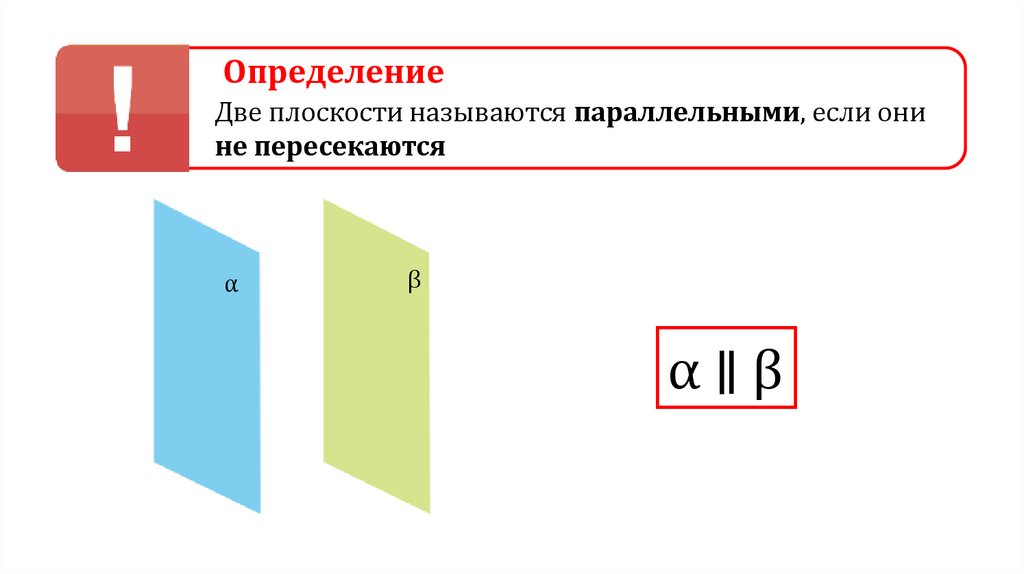
Определение
Две плоскости называются параллельными, если они
не пересекаются
α
β
α∥β

4.

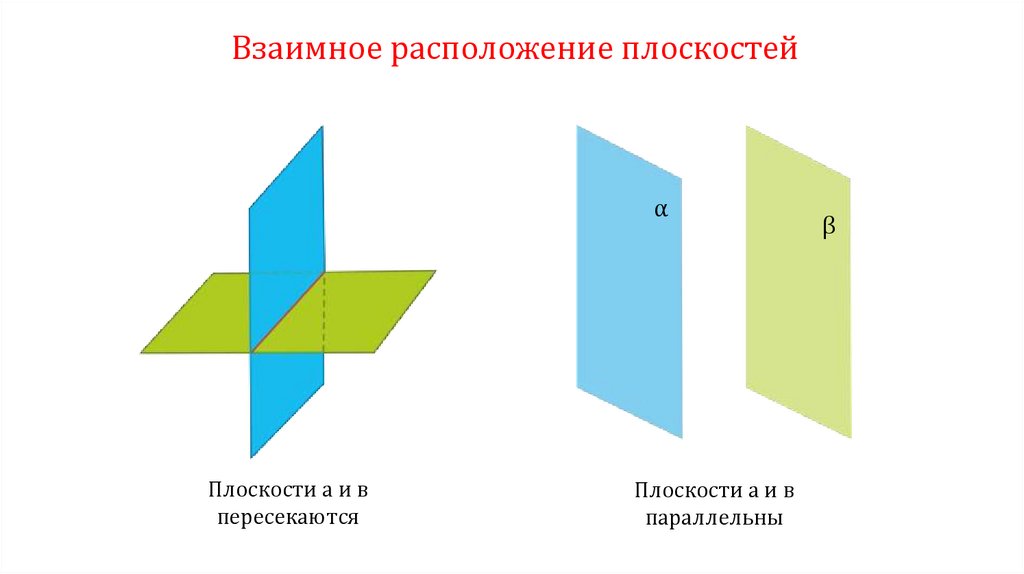
Взаимное расположение плоскостей
α
α
β
Плоскости а и в
пересекаются
Плоскости а и в
параллельны
β

5.

Теорема
(признак параллельности плоскостей)
Если две пересекающиеся прямые одной
плоскости соответственно параллельны
двум пересекающимся прямым другой
плоскости, то эти плоскости параллельны

6.

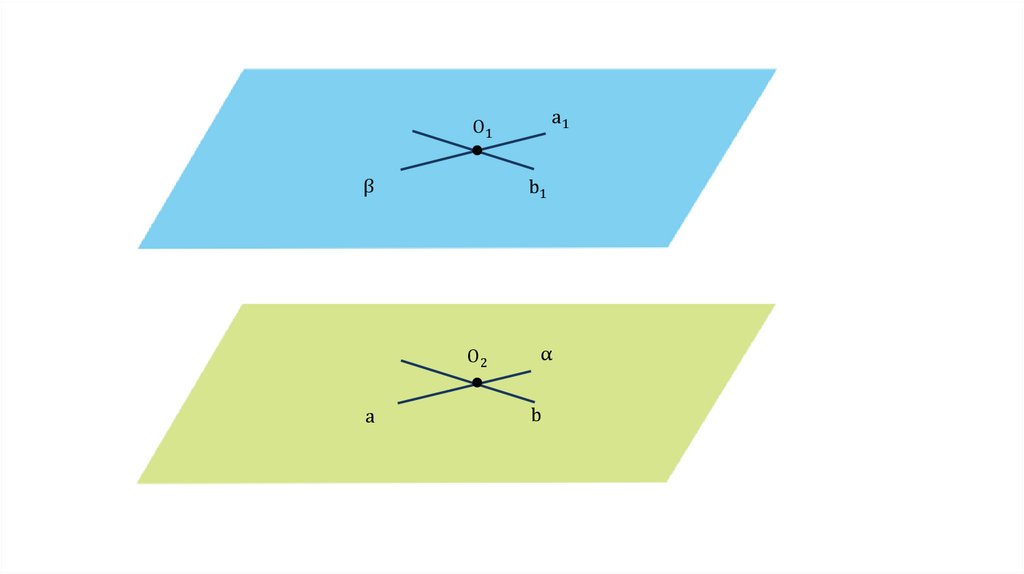
Доказательство.
Рассмотрим две плоскости:
.
В плоскости лежат пересекающиеся прямые a1 и b1, а в плоскости
пересекающиеся прямые a2и b2.
Докажем, что
.
параллельные им
Доказательство. Рассуждаем методом от противного.
Предположим, что плоскости
некоторой они пересекаются.
не параллельны. Тогда существует прямая c, по
Так как прямая a1 параллельна прямой a2 , лежащей в плоскости , то прямая a1
параллельна плоскости .
Аналогично, прямая b1 параллельна плоскоcти
.
Теперь можно воспользоваться свойством прямой, параллельной плоскости.

7.

a1
O1
β
b1
O2
a
α
b

8.

Так как плоскость проходит через прямую a1, параллельную другой плоскости , и
пересекает эту плоскость, то линия пересечения плоскостей c будет параллельна прямой
a1, т.е.
Но плоскость проходит и через прямую b1, параллельную плоскости , поэтому
Таким образом, через точку O1 проходят две прямые a1 и b1 , параллельные прямой c.
Но это невозможно, через O1 может проходить только одна прямая, параллельная с.
Предположив, что
Теорема доказана.
мы пришли к противоречию. Следовательно,
.
.

9.

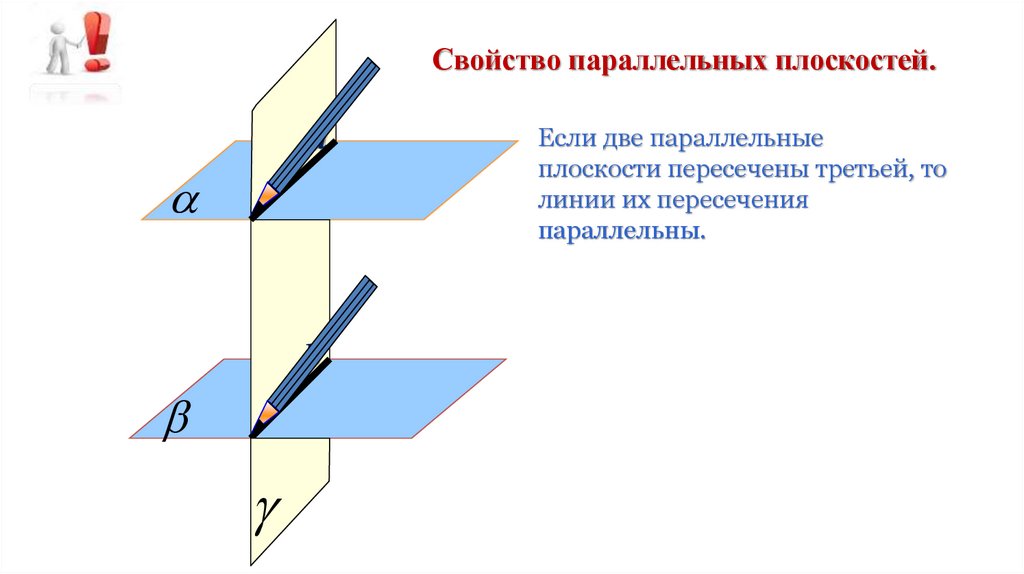
Свойство параллельных плоскостей.
а
b
Если две параллельные
плоскости пересечены третьей, то
линии их пересечения
параллельны.