Основные понятия теории моделирования. Лекция №1

1. ЛЕКЦИЯ №1

Курс: Модели информационных процессов и систем
Тема: Основные понятия теории моделирования
1. Основные понятия
2. Понятие системы
3. Имитационная модель
4. Общие принципы построения моделей
5. CALS - технология
6. Информационные технологии

2. 1. Основные понятия

2
Моделирование – это метод познания окружающего мира, состоящий в создании и
исследовании моделей.
Моделирование представляет собой исследование каких-либо явлений, процессов
или систем объектов путем построения и изучения их моделей, а также
использование моделей для определения или уточнения способов построения
вновь создаваемых объектов.
Модель – некий новый объект, который отражает существенные особенности
изучаемого объекта или процесса.
Один и тот же объект может иметь множество моделей, а разные объекты могут
описываться одной моделью.
Процесс - последовательное изменение состояния системы.
Следует заметить, что одной из важнейших проблем современной науки и техники
является разработка и внедрение в практику проектирования систем различного
назначения новейших методов и моделей исследования их характеристик,
включая сложные информационно-управляющие и информационновычислительные системы различных уровней.
Для описания данной проблемы выделим следующие понятия: система, модель
системы, информационная система, информационная технология

3. 1. Основные понятия

3
Преимущества моделирования:
1. в модели выбирается лишь часть свойств (только существенные свойства) –
все свойства оригинала не рассматриваются, поэтому – экономия ресурсов.
Обычно при моделировании число факторов велико. К сожалению, чем
меньше мы знакомы с изучаемым оригиналом, тем больше стараемся учесть
факторов, которые, как нам представляется, способны влиять на результаты
исследования. «Как правило, степень понимания явления обратно
пропорциональна числу переменных, фигурирующих в его описании».
Большинство исследуемых систем работает в соответствии с принципом
Парето – существенны лишь некоторые из множества факторов.
Действительно, в большинстве систем 20% факторов определяют 80%
свойств системы, а остальные 80% факторов определяют лишь 20% ее
свойств.
2. разрабатываемые модели могут быть систематизированы и храниться в базе. На
основе уже разработанных моделей могут быть созданы новые модели,
происходит накопление опыта исследователей.

4. 1. Основные понятия

4
Классический и системный подходы к математическому моделированию
На начальной стадии появления моделирования для построения модели
исследуемого объекта использовались фундаментальные законы природы,
которые проявляются в виде функциональных связей между небольшим
количеством факторов.
Явления и объекты, достаточно точно и однозначно описываемые небольшим
количеством факторов, получили название простых систем или хорошо
организованных систем. Для такого класса объектов исследование самого
объекта можно заменить исследованием отдельных его частей,
изолированных друг от друга. Экспериментальные исследования хорошо
организованных систем заключались в наблюдении за результатом изменения
одного фактора при постоянстве прочих.
Такой подход вполне соответствует человеческой логике, поддается осмыслению и
объяснению, передаче накопленных знаний, и получил название
индуктивного или классического подхода к математическому
моделированию. Примерами построения моделей на основе классического
подхода могут служить классические законы механики, физики, химии.

5. 1. Основные понятия

5
Классический и системный подходы к математическому моделированию
Однако при исследовании объектов, описываемых в виде сложных динамических
систем или трудно формализуемых систем, в которых нельзя разделить
отдельные явления и процессы, необходимо создавать модель объекта с
учетом цели его функционирования, т.е. учитывать так называемое
интегративное свойство объекта. В этом случае, вместо моделей,
построенных на законах природы, приходится применять модели,
учитывающие закономерности, свойственные исследуемому объекту.
Такой подход к созданию модели объекта получил название системного подхода.
Построенная в соответствии с этим принципом модель объекта, позволяет
исследовать поведение объекта для различных условий его работы и выбрать
наиболее оптимальный вариант его использования, исходя из заданных целей
функционирования

6. 1. Основные понятия

6
Классификация моделей
Физическое моделирование
Физическое (или натурное) моделирование. Этот вид моделирования основан на
изучении явлений на моделях одной физической природы с оригиналом. При
физическом моделировании сохраняют особенности поведения объекта
исследования, что существенно облегчает получение требуемых результатов,
так как для модели выбирают наиболее удобные геометрические размеры и
диапазоны изменения физических величин. Метод физического
моделирования имеет очень важное значение в том случае, когда в комплекс
явлений, характеризующих исследуемый процесс, входят такие явления,
которые не поддаются математическому описанию.

7. 1. Основные понятия

7
Классификация моделей
Математическое моделирование
Математическое моделирование можно определить как совокупность
математических соотношений, определяющих процесс изменения состояния
объекта в зависимости от внешних воздействий, начальных условий и
момента времени.
Главное преимущество математического моделирования перед физическим
заключается в возможности исследования явлений природы, трудно
поддающихся изучению, используя хорошо изученные явления. При
математическом моделировании более наглядно, чем при физическом,
осуществляется индикация и регистрация результатов исследований: можно
просто варьировать в широких пределах исходные данные задачи для выбора
оптимальных (по заданному критерию) параметров исследуемой системы,
время решения задачи, по желанию исследователя, может быть изменено в
широких пределах.
По принципам построения математические модели разделяются на
аналитические, компьютерные и имитационные

8. 1. Основные понятия

Классификация моделей
Аналитические модели
Линейные математические модели
В качестве примера построения аналитической модели рассмотрим построение
простейшей модели популяций, называемая моделью Мальтуса или простой
экспоненциальной моделью роста народонаселения.
В основе построения данной модели находится простое утверждение – скорость
изменения населения со временем t пропорциональна его текущей
численности N(t), умноженной на сумму коэффициентов рождаемости α(t) и
смертности β(t). В результате получим следующее линейное
дифференциальное уравнение:
dN (t )
(t ) (t ) N (t )
dt
8

9. 1. Основные понятия

Классификация моделей
Аналитические модели
Линейные математические модели
Интегрирование данного уравнения приводит к следующему решению:
t
N (t ) N (0) exp (t ) (t ) dt
0
где:
N (0) N (t t0 )
начальная численность населения.
Сформируем исходные данные и проведем расчеты для следующих
вариантов:
1 - (N(0)=2; α=4; β=1); 2 - (N(0)=2; α=3; β=1); 3 - (N(0)=2; α=2; β=1);
4 - (N(0)=2; α=1; β=1);
5 - (N(0)=2; α=1; β=2); 6 - (N(0)=2; α=1; β=3); 7 - (N(0)=2; α=1; β=4).
9

10. 1. Основные понятия

Классификация моделей
Аналитические модели
Линейные математические модели
На рисунке приведены графики функций N(t) при постоянных значениях α и β.
1. - (N(0)=2; α=4; β=1);
2. - (N(0)=2; α=3; β=1);
3. - (N(0)=2; α=2; β=1);
4. - (N(0)=2; α=1; β=1);
5. - (N(0)=2; α=1; β=2);
6. - (N(0)=2; α=1; β=3);
7. - (N(0)=2; α=1; β=4).
N(t)
4
2
0
0
0.2
0.4
0.6
t
0.8
1
10

11. 1. Основные понятия

11
Классификация моделей
Аналитические модели
Линейные математические модели
При α = β численность населения остается постоянной. В этом случае решением
уравнения является равновесная величина N(0).
Равновесие между рождаемостью и смертностью является неустойчивым. Даже
небольшое нарушение равенства α = β приводит к большому отклонению
функции N(t) от равновесного значения N(0).
Верхняя часть графика, находящаяся выше равновесного значения N(0)
соответствует α > β, нижняя часть - α < β. В первом случае значение N(t)
стремится к бесконечности, что приводит к перенаселению, а во втором
случае к вымиранию.

12. 1. Основные понятия

12
Классификация моделей
Аналитические модели
Линейные математические модели
Такие выводы послужили основанием для опасения Мальтуса о грядущем
демографическом кризисе. Полученная модель роста населения является
линейной моделью, поскольку получена на основе анализа линейного
дифференциального уравнения. Поэтому и рассмотренная модель тоже
относится к классу линейных. Это простейший в смысле получения
аналитических результатов класс моделей.
Понятие линейности в этом случае означает, что выполняется принцип
суперпозиции, т.е. любая линейная комбинация решений (например, их
сумма) также является решением задачи. Пользуясь принципом
суперпозиции, можно легко найти решение в каком-либо частном случае, а
затем построить решение для более трудной задачи. О качественных
свойствах общего более трудного решения можно судить из анализа частного.

13. 1. Основные понятия

13
Классификация моделей
Аналитические модели
Нелинейные математические модели
Большинство реальных процессов и соответствующих им математических
моделей – не линейны. В этом случае для этих моделей не выполняется
принцип суперпозиции и поэтому знание о поведении части объекта не
гарантирует знания о поведении всего объекта.
Рассмотрим следующую модель популяции при ограниченности доступных
ресурсов. Предположим, что численность популяции ограничена ресурсами,
которыми может обеспечит окружающая среда. Обозначим эту равновесную
численность популяции – Np. Тогда будем считать, что и скорость изменения
численности популяции пропорционально самой численности, умноженной
(в отличие от модели Мальтуса) на величину ее отклонения от равновесного
значения. В соответствии с данными требованиями скорость изменения
популяции может быть записана в виде следующей формулы:
N (t )
dN (t )
1
N (t )
Np
dt

14. 1. Основные понятия

Классификация моделей
Аналитические модели
Нелинейные математические модели
dN (t )
N (t )
1
N (t )
N
dt
p
Выражение в скобках (1-N/Np) обеспечивает насыщение численности – скорость
роста не постоянна (в отличие от модели Мальтуса) и стремится к нулю при
N (t ) N p
Полученное уравнение представим в следующем виде:
dN
dN
dt
Np N N
Проинтегрировав это уравнение, получим следующее:
ln N p N ln N t C
14

15. 1. Основные понятия

Классификация моделей
Аналитические модели
Нелинейные математические модели
Постоянная интегрирования С может быть найдена из условия
N (0) N (t t0 )
отсюда получим :
ln N p N ln N t C
N (0)
C ln
N N (0)
p
Подставляя полученное значение для С в уравнение получим следующее
выражение
N (t ) N p
N (0)
N (0)
e t N (t )
e t
N p N (0)
N p N (0)
15

16. 1. Основные понятия

16
Классификация моделей
Аналитические модели
Нелинейные математические модели
Окончательное решение нашей задачи может быть записано в следующем виде:
N (0) e t
N (t ) N p
N p N (0) 1 e t
Полученная функция N(t) называется логистической.

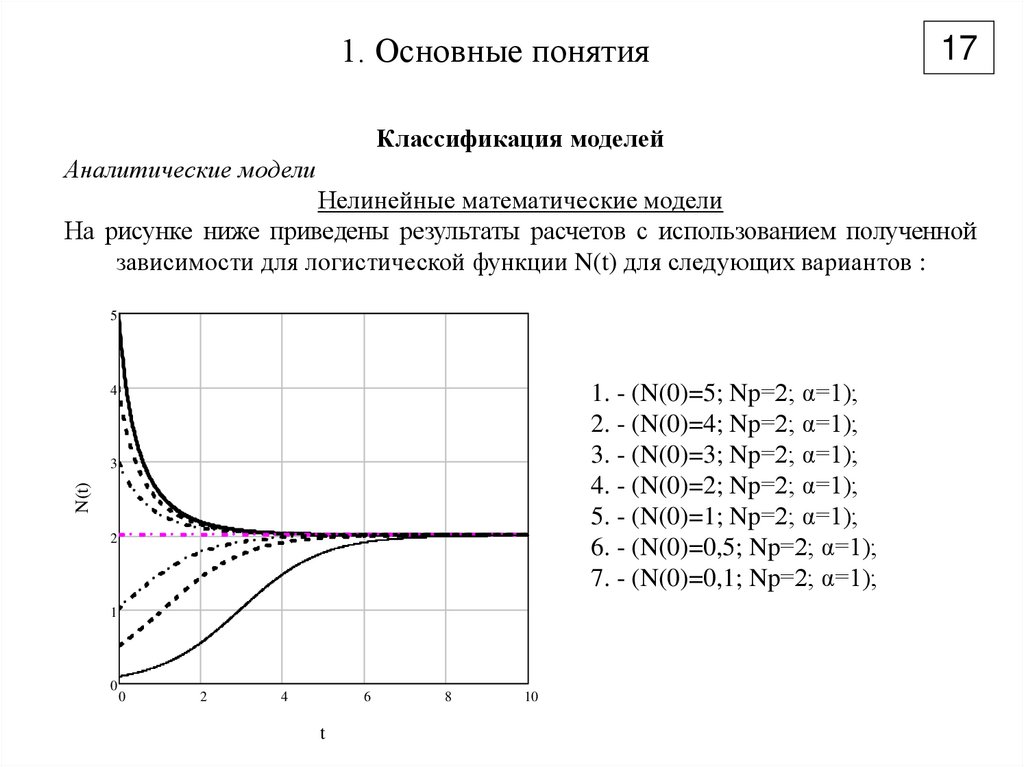
17. 1. Основные понятия

17
Классификация моделей
Аналитические модели
Нелинейные математические модели
На рисунке ниже приведены результаты расчетов с использованием полученной
зависимости для логистической функции N(t) для следующих вариантов :
5
1. - (N(0)=5; Np=2; α=1);
2. - (N(0)=4; Np=2; α=1);
3. - (N(0)=3; Np=2; α=1);
4. - (N(0)=2; Np=2; α=1);
5. - (N(0)=1; Np=2; α=1);
6. - (N(0)=0,5; Np=2; α=1);
7. - (N(0)=0,1; Np=2; α=1);
4
N(t)
3
2
1
0
0
2
4
6
t
8
10

18. 1. Основные понятия

18
Классификация моделей
Аналитические модели
Нелинейные математические модели
Для данной модели независимо от начального значения N(0) численность
популяции стремится к равновесному состоянию Np. Тем самым доказывая,
что равновесие в данном случае имеет устойчивый характер.
В отличие от модели Мальтуса логистическая модель более реалистична. Однако
является более сложной.
Следует заметить, что еще более реалистичной может быть построена
имитационная модель с использованием многоагентной методологии и
программной системы AnyLogic.

19. 1. Основные понятия

19
Классификация моделей
Компьютерные модели
Подводя итог выше сказанному можно сделать вывод, что Модель является
базовым понятием для любых областей знаний, использующих аппарат
математики, поскольку каждая попытка работать в точных терминах с
реальным явлением должна начинаться с описания его формальной Модели.
Именно Модель представляет Объект исследования и определяет характер
формального аппарата, используемого для описания Задачи и выполнения
необходимых вычислений
Модель является наиболее естественной формой спецификации реальной Задачи.

20. 1. Основные понятия

20
Классификация моделей
Компьютерные модели
Если использование аналитических методов для решения полученной Задачи
невозможно, то приходится прибегать к численным методам.
В этом случае для получения необходимой информации об Объекте исследования
для имеющейся Модели необходимо иметь Метод (как правило, численный)
и
Алгоритм (представляющий собой инструмент, являющейся ключом к
используемому компьютеру) .
Объединение понятий: математической модели, численных методов и алгоритмов,
реализованных в виде компьютерных программ, приводит к понятию
Компьютерной модели.

21. 1. Основные понятия

21
Классификация моделей
Компьютерные модели
Вычислительный алгоритм, используемый в Компьютерной модели, должен
удовлетворять определенным требованиям.
Во первых, решение должно быть получено с заданной точностью и за разумное
по возможности за минимальное число действий.
Во вторых объемы обрабатываемой информации не могут превышать емкости
машинной памяти.
В третьих в процессе вычислений нельзя допускать появления больших или
малых чисел, которые не воспринимаемы компьютером.
Создание Компьютерной модели дает возможность провести полноценное
обследование объекта получить исчерпывающую информацию
количественных характеристик и изучить основные качественные его
свойства.

22. 1. Основные понятия

22
Классификация моделей
Компьютерные модели
Компьютерная модель - модель, исследуемого объекта, выполненная в
компьютерной (вычислительной) среде и представляющая собой
совокупность данных и программного кода, необходимого для работы с
данными. (ГОСТ Р 57412-2017. Компьютерные модели в процессах
разработки, производства и эксплуатации изделий.)
Данный ГОСТ устанавливает общие требования к Компьютерной модели на всех
этапах жизненного цикла промышленной продукции.

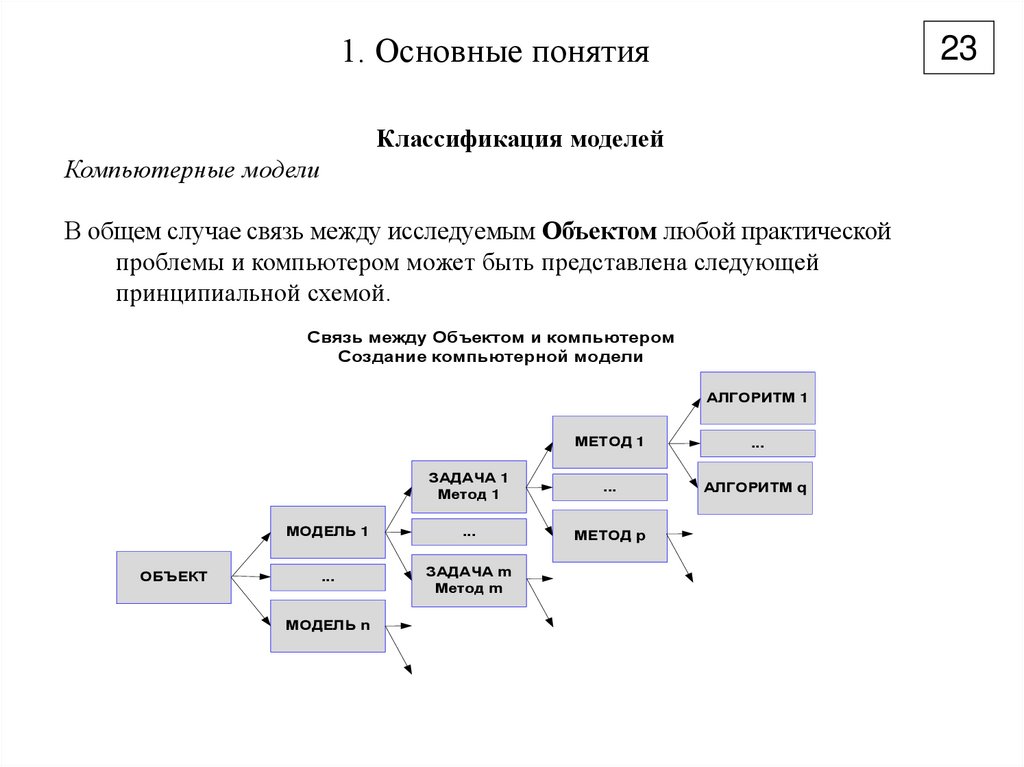
23. 1. Основные понятия

23
Классификация моделей
Компьютерные модели
В общем случае связь между исследуемым Объектом любой практической
проблемы и компьютером может быть представлена следующей
принципиальной схемой.
Связь между Объектом и компьютером
Создание компьютерной модели
АЛГОРИТМ 1
ОБЪЕКТ
МЕТОД 1
...
ЗАДАЧА 1
Метод 1
...
АЛГОРИТМ q
МОДЕЛЬ 1
...
МЕТОД p
...
ЗАДАЧА m
Метод m
МОДЕЛЬ n

24. 1. Основные понятия

Классификация моделей
Компьютерные модели
В качестве примера рассмотрим непрерывный производственный процесс, для
управления которого выделены специальные параметры управления,
участвующие в описании технологической части модели рассматриваемого
процесса. В качестве одного из факторов выделенной группы параметров
выделим – температуру T, как один из важных параметров для обеспечения
регулирования условий протекания производственного процесса.
Для описания распределения температуры в сплошной среде известно
математическое уравнение параболического типа:
2U 2U 2U U
x 2 y 2 z 2
t
где U – искомая функция (в рассматриваемом случае - температура),
x, y, z – пространственные координаты,
t- время протекания процесса
24

25. 1. Основные понятия

25
Классификация моделей
Компьютерные модели
Приведенное выше уравнение в нашем представлении будет являться
математической Моделью для определения заданного параметра T.
Исходное уравнение совместно с условиями однозначности, включающими
геометрические, физические, граничные и начальные условия, определяют
Задачу.
Для решения сформированной Задачи необходимо выбрать численный Метод.
В качестве Метода можно выбрать Метод конечных разностей или Метод
конечных элементов.
На основе выбранного Метода строится дискретная модель, приводящая к
системе линейных алгебраических уравнений.
Для решения системы полученных уравнений должен быть реализован Алгоритм
в виде программы, либо использована стандартная математическая
библиотека.

26. 2. Понятие системы

Система – сложный объект, состоящий из взаимосвязанных частей
(элементов). Всякая система имеет определенное назначение (цель).
Кроме того, всякая система определяется не только составом своих частей, но и
порядком и способом объединения этих частей в единое целое, т.е.
структурой.
Структура – совокупность связей между элементами системы. Структура
систем зависит от поставленной цели.
Отметим важный фактор в определении системы – ее сложность. В связи с этим,
перечислим основные отличительные признаки сложных систем:
1. Сложность функции, выполняемой системой и направленной на достижение
заданной цели функционирования. Заметим, что цель функционирования
может быть не одна, а несколько, т.е. целевая функция может оказаться
многоцелевой (многокритериальной).
26

27. 2. Понятие системы

Отличительные признаки сложных систем (продолжение):
2. Наличие большого количества связей - взаимно связанных и
взаимодействующих между собой элементов.
Понятие элемента при разбиении системы является относительным. Заметим, что
внутренняя структура элемента в этом случае, т.е. при разбиении системы на
элементы, не интересна, существенными для элемента являются лишь такие
свойства, которые определяют взаимодействие с другими элементами, или
влияют на свойства самой системы.
Под “связями” между элементами понимается некоторый виртуальный канал, по
которому осуществляется обмен между элементами и внешней средой
веществом, энергией, информацией.
27

28. 2. Понятие системы

28
Отличительные признаки сложных систем (продолжение):
3. Возможность разбиения системы на подсистемы, цели функционирования
которых подчинены общей цели функционирования всей системы.
Очень часто элементы системы объединяют в группы, которые называют
подсистемами. Отличительными характеристиками подсистем является
выполнение ими самостоятельных функций, которые могут быть
использованы в дальнейшем, при изменении структуры системы.
4. Наличие управления (имеющего, в свою очередь, иерархическую
структуру), разветвленной информационной сети и интенсивных потоков
информации.
В сложных системах, большое значение играют функции, связанные с
управлением системой. Управление включает: сбор, переработку информации
о системе и принятие решений. Управление может быть централизованным,
децентрализованным и иерархическим, при котором имеется несколько
уровней управления. .

29. 2. Понятие системы

Связи между элементами системы могут быть представлены в виде
математического описания:
1. функциональной связи вектор – функций
y f x, t
2. неявной функциональной связи вектор – функций
F y, x, t 0
3. системы линейных алгебраических уравнений,
4. системы обыкновенных дифференциальных уравнений,
5. дифференциальных уравнений с частными производными.
29

30. 3.Имитационная модель

30
Для моделирования сложных систем с возможностью моделирования случайных
процессов используются имитационные модели.
Имитационная модель позволяет получить информацию о поведении реальной
системы на основе разработанной компьютерной модели. Отметим, также
важную особенность имитационных моделей – возможность моделирования
не только детерминированных, но и случайных факторов. В этом случае, при
возможности моделирования случайных факторов, модель называется
стохастической моделью.
Источниками возникновения случайных факторов являются внешние воздействия
(это воздействия внешней среды), и внутренние воздействия, связанные с
возникновением различных ошибок, шумов внутри самой системы.

31. 3. Имитационная модель

31
В общем виде имитационное моделирование совмещает в себе как особенности
экспериментального подхода, так и возможности использования
вычислительных средств. По сути, исследователь проводит вычислительные
эксперименты с имитационной моделью. Полученные в этом случае
результаты требуют специальной статистической обработки. Поэтому при
проведении имитационного моделирования важную роль играют также
планирование эксперимента с имитационной моделью и статистическая
обработка и анализ результатов исследования.
Во многих случаях имитационное моделирование является мощным средством
исследования поведения реальных систем, дает возможность получить
требуемую информацию о поведении реальной системы из анализа работы ее
компьютерной модели. Полученная таким образом информация используется
для проектирования реальной системы, выделяя при этом проблемные места
в системе и предлагая оптимальные решения.

32. 4. Общие принципы построения моделей

32
Различают следующие принципы построения моделей:
1. феноменологический,
2. системный.
Феноменологический принцип основан на представлении модели в виде
«черного ящика».
вход
выход
модель
X
Y
В этом случае модель можно представить в виде:
Y=F(X),
где Y– вектор выходных характеристик,
X- вектор входных характеристик,
F(X) - оператор преобразования входных характеристик в выходные
Как правило, нахождение оператора F(x) для феноменологических
моделей основано на методах математической статистики – регрессионный
анализ.

33. 4. Общие принципы построения моделей

33
Системный принцип построения моделей предполагает построение
структуры модели в виде системы.
Важным свойством системы является то, что она обладает
интегративным свойством, т.е. таким свойством, которое не является суммой или
средним совокупности элементов.
Интегративное свойство имеет информационную природу. Это значит, что
система тоже имеет информационную природу. Чтобы совокупность элементов стала
системой, она должна структурироваться, т.е. на совокупность элементов должна
быть нанесена информация.
Пример. ЭВМ состоит из множества деталей. Объединяя (связывая) эти объекты мы
еще не приходим к интегративному свойству – необходима настройка. Еще более
процесс усложняется, если рассматривать вычислительную систему (ВС),
включающую аппаратное обеспечение и программное обеспечение. В этом случае
необходимо настраивать и аппаратное обеспечение и программное обеспечение.
Процесс настройки означает, что на совокупность элементов наносится информация.

34. 4. Общие принципы построения моделей

34
Представленное выше определение системы показывает, когда объект надо
моделировать как систему, а когда нет.
Если исследователя интересует интегративное свойство, то объект надо
рассматривать как систему.
Если интегративное свойство исследователю не интересно, то объект как
система не рассматривается.
Создание и поддержание структуры системы требует ресурсы. Ресурсы
расходуются на доставку материи (энергии) и на внесение информации. Материю
(энергию) надо доставить в нужное время в строго определенную точку.
Можно подобрать оптимальное соотношение между вложенной в систему
материей и информацией, чтобы количество ресурса для получения интегративного
свойства было минимальным. Это задача является задачей моделирования.

35. 4. Общие принципы построения моделей

35
Описание системы может быть:
- внешним – когда исследуются элементы системы и их связи,
- внутренним – когда исследуются функции системы, направленные на
достижение заданной цели.
Внешнее описание формирует понятие структурной модели системы,
которая дает описание компонентов системы, системообразующих связей и потоков,
идущих по этим связям.
Внутренне описание формирует понятие функциональной модели
системы, которая дает описание
последовательности действий системы для
достижения интегративного свойства. Функциональное описание оценивает
функции системы; является менее общим, чем структурное описание.
Структурная и функциональная модели – статичны, т.е. являются статическими
моделями.
Процессы
функционирования
описываются
динамическими
моделями.
Функционирование – переход системы из одного состояния в другое, проявление
функций во времени.
Динамическая модель дает описание зависимости свойств системы от времени, а
также от начальных и граничных условий, т.е. отображает причинно-следственные
связи.

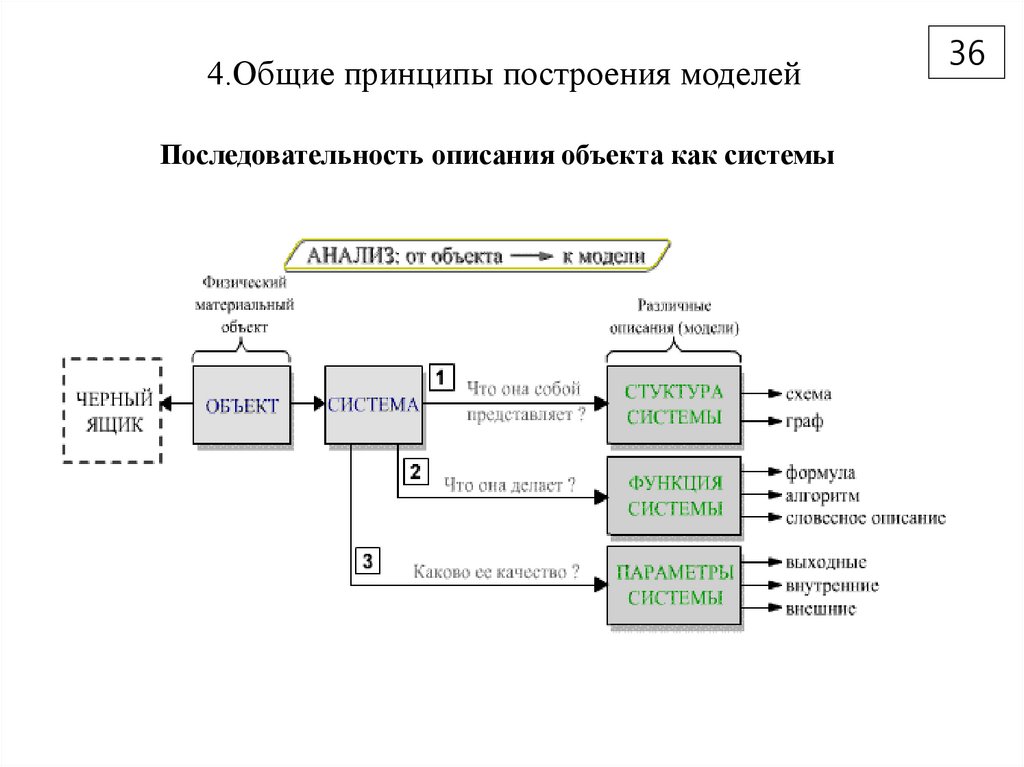
36. 4.Общие принципы построения моделей

Последовательность описания объекта как системы
36

37. 5.CALS – технология

Основные понятия
Особенностью современного развития общества является интенсивное внедрение
новых информационных технологий во все сферы его деятельности. Важное
место в структуре информационного общества занимают математические
модели, обеспечивающие надежные способы переработки исходного
информационного сырьевого продукта в конечный полезный информационный
продукт (информационный ресурс), представляющий самостоятельную
ценность. Накопление и использование полученного информационного ресурса
является важным показателем технологического уровня развития общества в
целом. Весьма перспективным направлением накопления и использования
информационного ресурса является компьютеризация производственной
деятельности. Информатизация технологических процессов позволяет
существенно повысить как производительность труда, так и качество
выпускаемой продукции.
В предлагаемом курсе «Модели информационных процессов и систем» будут
рассмотрены разнообразные математические модели, полезность изучения
которых необходима для разных специальностей.
3
7

38. 5.CALS – технология

3
8
Следует подчеркнуть, что рассмотренные математические модели получили также
широкое использование в том числе и в производственной деятельности, в
рамках так называемой CALS-технологии. Название CALS (Continuous
Acquisition and Life cycle Support) в переводе означает – непрерывная
информационная поддержка поставок и жизненного цикла производственных
изделий. Применение CALS-технологий позволяет предприятию существенно
сократить затраты и трудоемкости процессов технической подготовки и
освоения производства новых изделий, затраты на эксплуатацию,
обслуживание и ремонты изделий, которые для сложной наукоемкой
продукции подчас равны или превышают затраты на ее закупку.

39. 5.CALS – технология

3
9
Концептуальная модель CALS (ИПИ)
Основу CALS-технологии составляет Интегрированная Информационная Среда
(ИИС), которая формирует Единое Информационное Пространство (ЕИП).

40. 5.CALS – технология

4
0
Основу ИПИ составляет Интегрированная Информационная Среда (ИИС)
эквивалентное понятие – Единое Информационное Пространство (ЕИП). На
практике термин ИИС используют в основном применительно к конкретному
предприятию, а ЕИП – применительно к виртуальному предприятию
(консорциуму).
Стадии жизненного цикла изделия:
1. Определение и анализ потребности.
2. Изучение реализуемости.
3. Определение требований.
4. Разработка и проектирование.
5. Производство.
6. Развертывание.
7. Эксплуатация поддержка.
8. Утилизация.

41. 5.CALS – технология

41
В ИИС информация создается, преобразуется, хранится и передается от одного
участника ЖЦ к другому при помощи программных средств,
объединенных на схеме в блок «Инструментарий». К числу таких средств
относятся:
- автоматизированные системы конструкторского и технологического
проектирования (CAE/CAD/CAM);
- программные средства управления данными об изделии (изделиях) (PDM);
- автоматизированные системы планирования и управления производством и
предприятием (MRP/ERP);
- программно-методические средства анализа логистический поддержки и ведения
баз данных по результатам такого анализа (LSA/LSAR);
- программные средства управления потоками работ (WF);
- методология и программные средства моделирования и анализа бизнеспроцессов (SADT) .
ИПИ-технологии реализуются силами многопрофильных рабочих групп,
объединяющих в своем составе экспертов различных специальностей.
Нормативную базу разработок составляют международные и национальные
стандарты, регламентирующие различные аспекты ИПИ-технологий

42. 5.CALS – технология

42
Интегрированная Информационная Среда (ИИС)
Производство и все процессы в нем принадлежат физическому миру, а процессы,
протекающие в компьютере – миру информации. Следовательно, необходимо
преобразование производственных проблем в информационные, а также
обратный переход из информационного мира в физический. По сути, это
проблема адекватного моделирования, т.е. установления соответствия (по
возможности взаимно однозначного) между физическим и информационным
пространством.

43. 5.CALS – технология

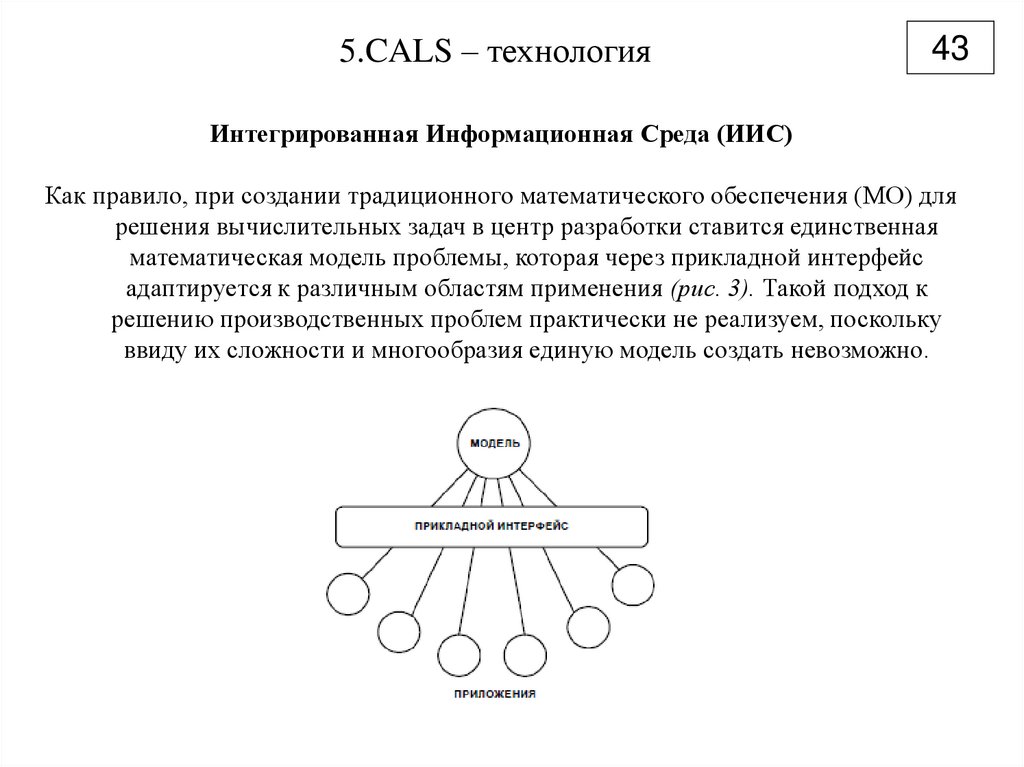
43
Интегрированная Информационная Среда (ИИС)
Как правило, при создании традиционного математического обеспечения (МО) для
решения вычислительных задач в центр разработки ставится единственная
математическая модель проблемы, которая через прикладной интерфейс
адаптируется к различным областям применения (рис. 3). Такой подход к
решению производственных проблем практически не реализуем, поскольку
ввиду их сложности и многообразия единую модель создать невозможно.

44. 5.CALS – технология

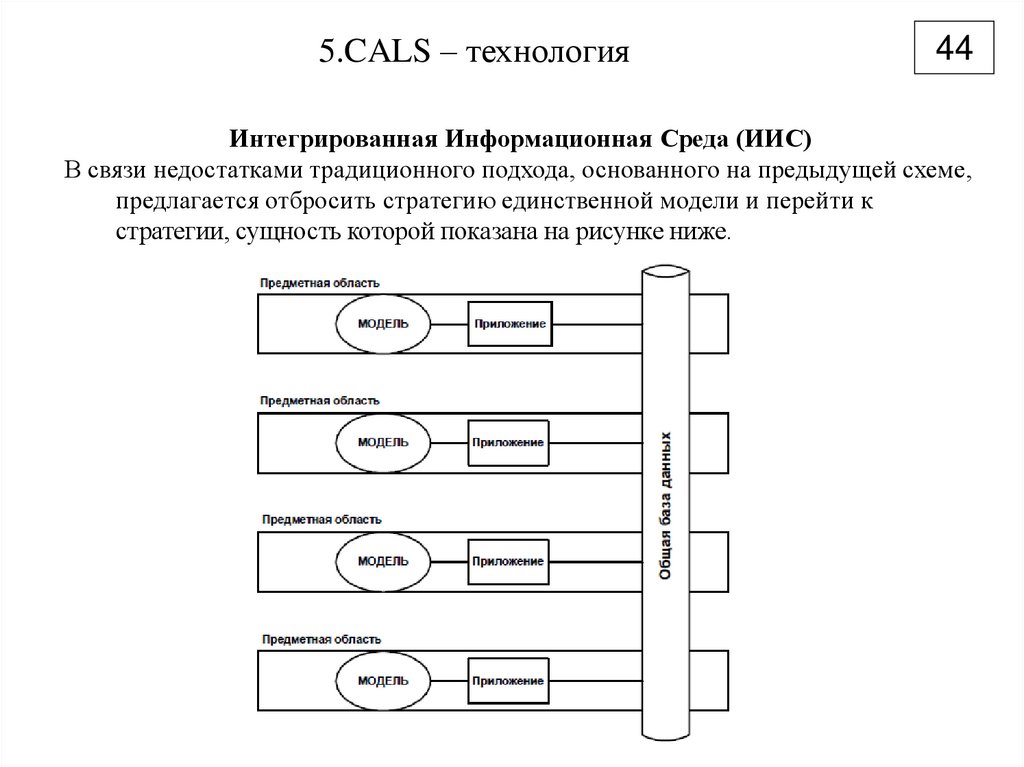
44
Интегрированная Информационная Среда (ИИС)
В связи недостатками традиционного подхода, основанного на предыдущей схеме,
предлагается отбросить стратегию единственной модели и перейти к
стратегии, сущность которой показана на рисунке ниже.

45. 5.CALS – технология

45
Интегрированная Информационная Среда (ИИС)
Здесь роль ядра системы играет не модель, а общая (интегрированная) база данных (ОБД),
к которой могут обращаться различные проблемно-ориентированные модели,
реализованные в форме программных приложений. Предполагается, что в ОБД
хранятся информационные объекты (ИО), адекватно отображающие в
информационном мире сущности физического мира: предметы, материалы, изделия,
процессы и технологии, разнообразные документы, финансовые ресурсы, персонал
подразделения и оборудование предприятия-изготовителя, эксплуатанта, сервисной и
ремонтной служб и т.д.
Используемые приложения обращаются в ОБД, находят в ней необходимые ИО,
обрабатывают их и помещают в ОБД результаты этой обработки.
Дальнейшее развитие информационных технологий (ИТ) привело к появлению объектноориентированного подхода, который позволил адекватно перевести многие процессы,
протекающие на предприятии, в виртуальное информационное пространство.
Сказанное относится, в частности:
1) к процессам конструкторской и технологической подготовки производства, в ходе которых
создается техническая документация различных видов и назначения,
2) к процессам управления на всех уровнях, в которых по необходимости приходится иметь
дело с большими объемами разнообразной информации.
На сегодняшний момент эти процессы в значительной мере состоят из операций создания,
преобразования, транспортировки и хранения информационных объектов в рамках
ИИС.

46. 6. Информационная система

46
В процессе развития вычислительной техники с появлением функции хранения
символьных данных и их обработки появляется возможность решения новых
задач (кроме чисто вычислительных), связанных с информационными
процессами управления производством.
Средства вычислительной техники стали внедряться в решение управленческих
задач, а системы, направленные на их решение стали называться
информационными. Появляется новое понятие информационная модель
предметной области.
На основе данной модели разрабатываются базы данных, позволяющие
организовать хранение, обработку и передачу информации в требуемом
формате. Данные функции, связанные с организацией хранения, обработки и
передачей информации, развиваются в новом нетрадиционные для
вычислительной техники направлениях, таких как – телекоммуникации, клиент
– серверная технология, интернет технология, корпоративные сети, OLAP –
технология, Data mining .

47. 6. Информационная система

47
В связи с этим, появляется система, структурными элементами которой являются
компьютеры, компьютерные сети, базы данных, технические и программные
средства связи, обслуживающий персонал, основная цель которой –
организация хранения, обработки и передачи информации. Такая система
получила название – информационная система.
Функциональная схема информационной системы представлена на рисунке.
ИМПО – информационная модель предметной области

48. 6. Информационная система

48
Информационная система представляет собой среду с организованной структурой,
в рамках которой осуществляется хранение, обработка и передача
информации.
Для решения этих задач и для обеспечения процесса обработки информации
необходимо иметь технические средства. Такими техническими средствами
являются аппаратное, программное и математическое обеспечение,
относящиеся к понятиям, связанным с информационными технологиями, т.е.
к понятию – процесса, состоящего из регламентированных правил и действий
над данными.

49. 6. Информационная технология

49
Выделим следующие информационные технологии, направленные на решение
различных задач, связанных с хранением, управлением и анализом
информационных ресурсов, а также комплексными задачами
информационной поддержки и управления производством:
OLAP – технология анализа информации,
Data Warehouse – хранилище данных,
Data Mining – анализ данных, установление связей между анализируемыми
данными,
MRP и ERP – системы поддержки управления производством,
CALS – информационная поддержка изделия на всех этапах его жизненного
цикла.

50. 6. Информационная технология

50
OLAP (OnLine Analytical Processing)
OLAP- это информационная технология, направленная на быстрый доступ к
большим данным и проведение многомерного анализа.
Следует заметить, что данные являются выборочными и имеют следующую
особенность: «набор классификационных атрибутов - число».
База данных OLAP состоит из одного или нескольких кубов, у которых ребра
соответствуют заданных атрибутам и каждая метка атрибута имеет свое
числовое значение (показатель). Кубы в зависимости от количества атрибутов
могут быть одномерными, двумерными или многомерными.

51. 6. Информационная технология

51
OLAP (OnLine Analytical Processing)
Сам по себе куб (многомерный) для непосредственного анализа не пригоден.
Поэтому из многомерного куба аналитик, проводящий анализ данных,
извлекает обычные двумерные таблицы, путем разрезания куба по
интересующим его меткам.
При проведении анализа данных с помощью OLAP аналитика, как правило,
интересуют исторические данные, которые отсутствуют в учетных
(операциональных) информационных системах. Поэтому в качестве
источника данных для OLAP используют не операциональные (учетные) базы
данных, ориентированные на обработку транзакций, а используют хранилища
данных Data Warehouse.
В настоящее время выпускается большое количество программных продуктов,
поддерживающих технологии OLAP.Среди поставщиков этих продуктов –
компании Oracle, IBM, Informix.

52. 6. Информационная технология

52
OLAP (OnLine Analytical Processing) Многомерный анализ данных
Пример использования технологии OLAP на основе программного модуля анализа данных SAP
Business Objects.
SAP Business Objects представляет аналитический модуль, предназначенный для проведения
многомерного анализа, формирования интегральной отчетности и подготовки данных для
конечного пользователя (руководителя) в удобном виде
На данном слайде приведен пример построения отчета в виде круговой диаграммы

53. 6. Информационная технология

OLAP (OnLine Analytical Processing)
Многомерный анализ данных
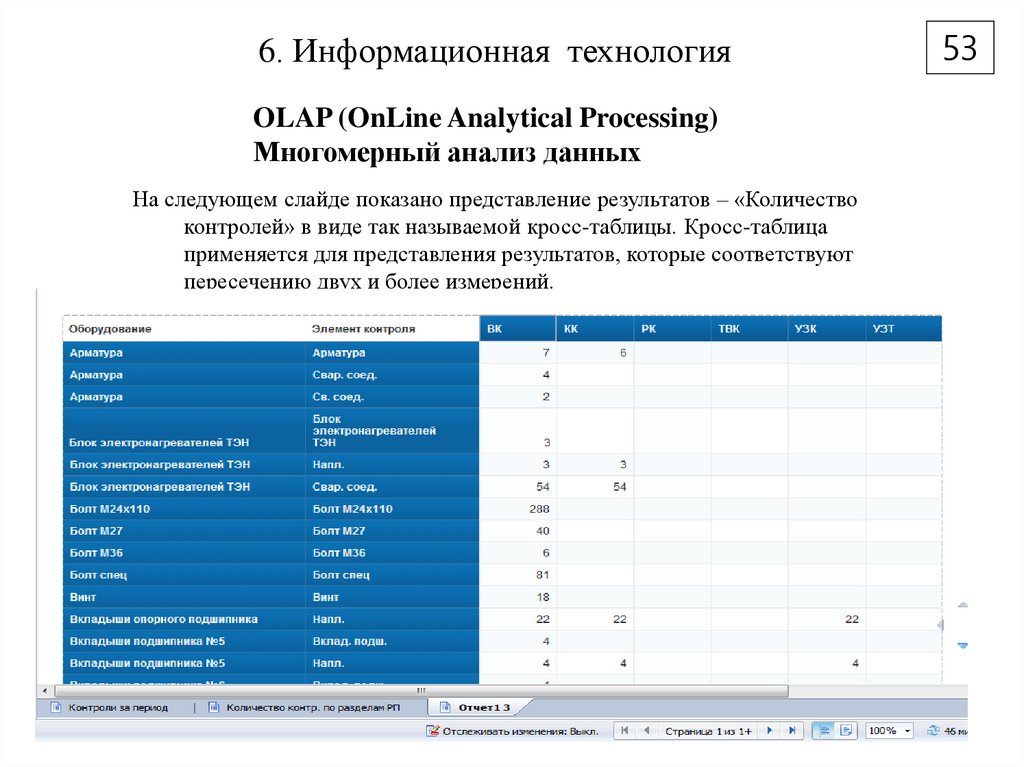
На следующем слайде показано представление результатов – «Количество
контролей» в виде так называемой кросс-таблицы. Кросс-таблица
применяется для представления результатов, которые соответствуют
пересечению двух и более измерений.
53

54. 6. Информационная технология

54
MRP и ERP – системы поддержки управления производством
В связи с развитием вычислительных систем, возникла идея использовать их
возможности для планирования деятельности предприятия, в том числе для
планирования производственных процессов.
Необходимость планирования обусловлена тем, что основная масса задержек
в процессе производства связана с запаздыванием поступления отдельных
комплектующих (точнее, с их поступлением позже или раньше требуемого
срока, в результате чего параллельно с уменьшением эффективности
производства на складах возникает недостаток или избыток материалов).
Кроме того, вследствие нарушения баланса поставок комплектующих,
возникают дополнительные осложнения с учетом и отслеживанием их
состояния в процессе производства, т. е. фактически невозможно было
определить, например, к какой партии принадлежит данный составляющий
элемент в уже собранном готовом продукте.
С целью предотвращения подобных проблем, была разработана методология
планирования потребности в материалах MRP (Material Requirements
Planning).

55. 6. Информационная технология

MRP и ERP – системы поддержки управления производством
Вследствие усовершенствования систем MRP и их дальнейшего
функционального расширения появился класс систем ERP.
Системы класса ERP отличает набор следующих свойств:
универсальность с точки зрения типов производств;
поддержка многозвенного производственного планирования;
более широкая (по сравнению с MRP) сфера интегрированного
планирования ресурсов;
включение в систему мощного блока планирования и учета
корпоративных финансов;
внедрение в систему средств поддержки принятия решений.
55

56. Литература

56
1) В.Н.Волкова, В.Н.Козлов. Моделирование систем и процессов. – М:Юрайт, 2014.- 591 с.
2) Советов Б.Я., Яковлев С.А. Моделирование систем: Учеб. для вузов – 3-е изд., перераб.и доп.
– М: Высш.шк., 2001. – 343с.:ил
3) Самарский А.А., Михайлов А.П. Математическое моделирование: Идеи. Методы. Примеры.
– 2-е изд., испр. – М: ФИЗМАТЛИТ, 2002. -320 с.
4) Бусленко Н.П. Моделирование сложных систем. Главная редакция физико-математической
литературы изд-ва «Наука», М., 1968, 356 стр.
5) Информационные системы и технологии: учебное пособие/ И.Л. Чудинов, В.В. Осипова;
Томский политехнический университет. – Томск: Изд-во Томского политехнического
университета. 2013 – 145 с.