Похожие презентации:
Алгебра. Задание №20
1.
Основной государственный экзамен2.
Задание 1.11
+
х2
Решите уравнение
2
–3= 0
х
y
x2
5
ОДЗ: x = 0.
1 + 2x – 3x2 = 0
– 3x2 + 2x + 1 = 0
(–1)
ГОТОВИМСЯ x
К ОГЭ
3x2 – 2x – 1 = 0
a = 3, b = – 2, c = – 1
D = b2 – 4ac
D = (–2)2 – 4 3 (–1) = 4 + 12 = 16 = 42
–b +
– D
x=
2a
2 +
– 4
x=
2 3
=
–2
1
= –
6
3
6
x2 =
=1
6
x1 =
ОДЗ
ОДЗ
1
Ответ: – ; 1.
3
3.
Задание 1.21
–
х2
Решите уравнение
ОДЗ: x = 0.
3
–4= 0
х
Применим способ введения
новой переменной (метод
замены)
t2 – 3t – 4 = 0
1
= t
х
a = 1, b = – 3, c = – 4
D = b2 – 4ac
–b +
– D
x=
2a
D = (–3)2 – 4 1 (–4) = 9 + 16 = 25 = 52
–2
+
t
=
= –1
3 – 5
1
2
t=
=
2 1
8
t2 =
=4
2
Вернёмся к замене.
1
= –1
х
x = –1
1
=4
х
ОДЗ
x=
1
4
ОДЗ
1
Ответ: –1; .
4
4.
Задание 1.3Решите уравнение
1
3
–
–4= 0
(х–3)2 х–3
ОДЗ: x = 3.
(x–3)2
1 – 3(x – 3) – 4(x – 3)2 = 0
1 – 3x + 9 – 4(x2 – 6x + 9) = 0
1 – 3x + 9 – 4x2 + 24x – 36 = 0
– 4x2 + 21x – 26 = 0
D = 212 – 4 (–4) (–26) = 441 – 416 = 25 = 52
–26 13
–21 +
5
x
=
–
x=
= 1 –8 = 4 = 3,25
2 (–4)
–16
x2 =
=2
ОДЗ
–8
ОДЗ
Ответ: 3,25;
2.
5.
Задание 2Решите уравнение
8 x 4 4 x x 2 3,5 2 x
2
8 x 2 x 3,5 2 x
8 x 2 x 3,5 2 x 0
2
2 x 8x 2 x 3,5 0
2
2 x 16 x 8x 3,5 0
2
8x 16 x 3,5 0
D 2 = kx – ac
Применим формулу
a2–2ab+b2 =(a – b)2
для трёхчлена 4–4x+x2=(2–x)2
Разложим левую часть на
множители. Вынесем за
скобки общий множитель –
двучлен (2–x)
2
4
D
–k +
x2= x –a 0 4
x 2
8x 2 16 x 3,5 0
Произведение равно
нулю, если один из
множителей равен нулю.
a=–8, k=8, c=–3,5
D 2
2
=8
–(–8)(–3,5)=64–28=36=6
4
–2 = 1
x
=
=0,25
1
–8
4
–8 +
6
– =
x=
–8
–14 = 7 =1,75
x2=
4
–8
Ответ:
2;
0,25;
1,75.
6.
Задание 3Решите уравнение
x 1 2 x 1 3 0
Применим способ введения
новой переменной (метод
замены)
Пусть (x – 1)22 =
4
1 t 2t 3 0
2
t >0
t1 t2 2
t1 t2 3
Это приведённое квадратное
уравнение (старший
коэффициент равен 1).
Найдем корни по теореме Виета.
(1)
x 1 2 1
нет решений
2
t1 1,
t 3
2
Вернемся к замене:
(2)
x 1 2 3
x 1 3
x 1 3
x 1 3
x 1 3
Ответ: 1– 3; 1+ 3.
7.
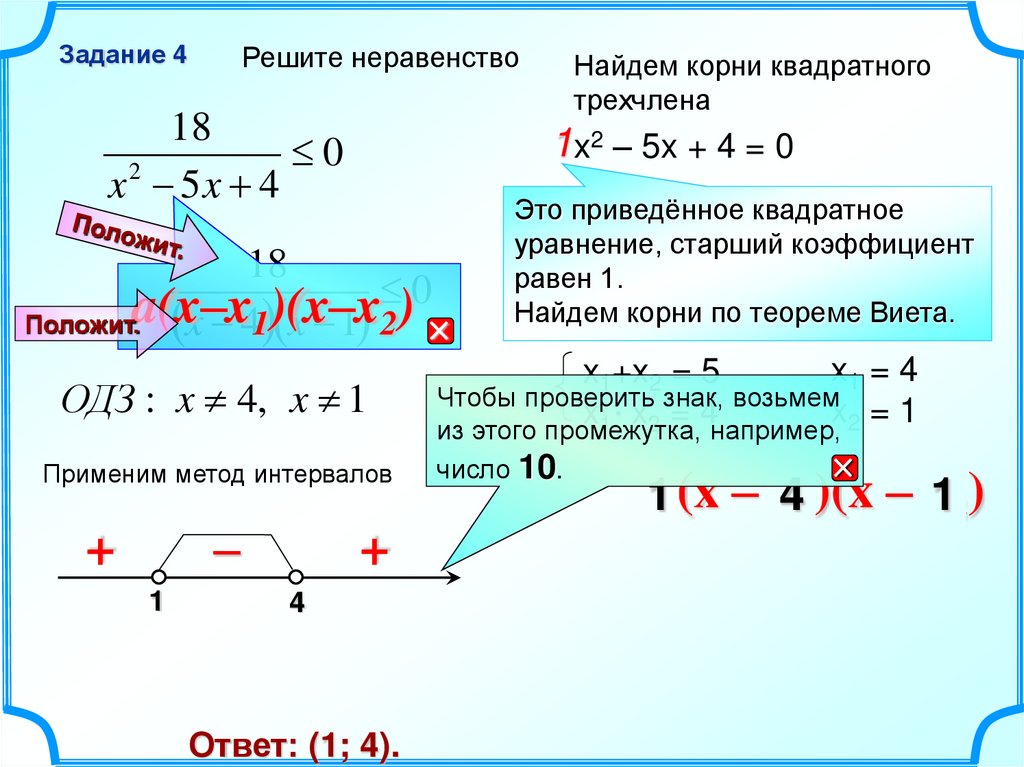
Задание 4Решите неравенство
18
0
2
x 5x 4
Найдем корни квадратного
трехчлена
1x2 – 5x + 4 = 0
18
)0
a(x–x
)(x–x
Положит. x 41 x 1 2
Это приведённое квадратное
уравнение, старший коэффициент
равен 1.
Найдем корни по теореме Виета.
ОДЗ : x 4, x 1
x1 = 4
x1+x2 = 5
Чтобы проверить знак, возьмем
x1 x2 = 4например,x2 = 1
из этого промежутка,
Применим метод интервалов
число 10.
–
+
1
+
4
Ответ: (1; 4).
1a(x – x41)(x – x12)
8.
Задание 5Решите неравенство
18
0
2
x 4 x 21
Найдем корни квадратного
трехчлена
18
)0
a(x–x
)(x–x
Положит. x 71
x 3 2
Это приведенное квадратное
уравнение, a = 1. Можно
применить теорему Виета.
x2 – 4x – 21 = 0
ОДЗ : x 7, x 3
Чтобы проверить
x1 = 7
x1 + x2знак,
= 4 возьмем
из этого промежутка, например,
x2 = – 3
x1 x2 = – 21
число 10.
Применим метод интервалов
–
–
+
–3
7
Ответ : ( ; 3); (7; )
1a(x – x71)(x – x32)
9.
19Решите неравенство
0
2
x 5 6
19
Разложить на множители
0
знаменатель можно по формуле
x 5 2 ( 66 )2
Задание 6
19
0
x 5 6 x 5 6
a2 – b2 =(a – b)(a+b)
ОДЗ : x 5 6 , x 5 6
Применим метод интервалов
–
–
+
–5– 6
Чтобы проверить знак,
возьмем из этого промежутка,
например, число 100.
–5+ 6
Ответ : ( 5 6 ; 5 6 )
10.
Задание 7Решите неравенство
x 5 3 x 5
2
x 5 3 x 5 0
Разложить на множители можно
способом вынесения за скобки
общего множителя – это двучлен
(x – 5)
2
x 5 x 5 3 0
x=5
x 5 0
x 5
x=5+ 3
–
5
+
5+ 3
Ответ : [5; 5 3 ]
x 5 3
Чтобы проверить знак,
возьмем из этого промежутка,
например, число 100.
Применим метод интервалов
+
x 5 3 0
11.
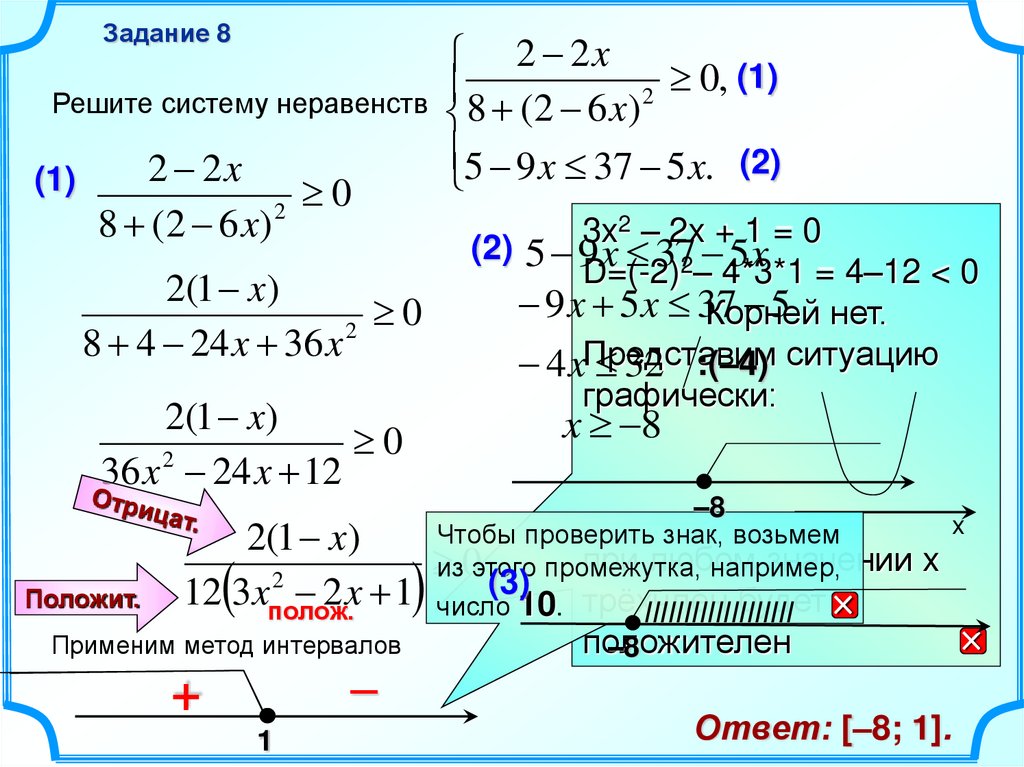
Задание 82 2x
0, (1)
2
Решите систему неравенств 8 (2 6 x)
5 9 x 37 5 x. (2)
2
2
x
(1)
0
2 – 2x + 1 = 0
8 (2 6 x) 2
3x
(2) 5 9x 372 5x
D=(-2) – 4*3*1 = 4–12 < 0
2(1 x)
9 x 5 x 37
5 нет.
Корней
0
8 4 24 x 36 x 2
4 xПредставим
32 :(–4) ситуацию
графически:
2(1 x)
x 8
0
36 x 2 24 x 12
–8
x
Чтобы проверить знак, возьмем
2(1 x)
при любом
значении x
из0этого
промежутка,
например,
2
(3)
12 3xполож.
2 x 1 число
Положит.
будет
10. трёхчлен
IIIIIIIIIIIIIIIIIII
положителен
Применим метод интервалов
–8
–
+
1
Ответ: [–8; 1].
12.
Задание 9Решите неравенство
3x 7
2
Разложить
на множители
2
можно по формуле
7знаменатель
x 3
a2 – b2 =(a – b)(a+b)
3x 7 7 x 3 0
3x 7 – 7 x 3 3x 7 7 x 3 0
3x 7 7 x 3 3x 7 7 x 3 0
2
2
4 x 4 11x 11 0
x=-1
x=1
Применим метод интервалов
–
–
+
-1
1
Ответ : ( ; 1)
3], (1
[3 ; )
Чтобы проверить знак,
возьмем из этого промежутка,
например, число 10.
13.
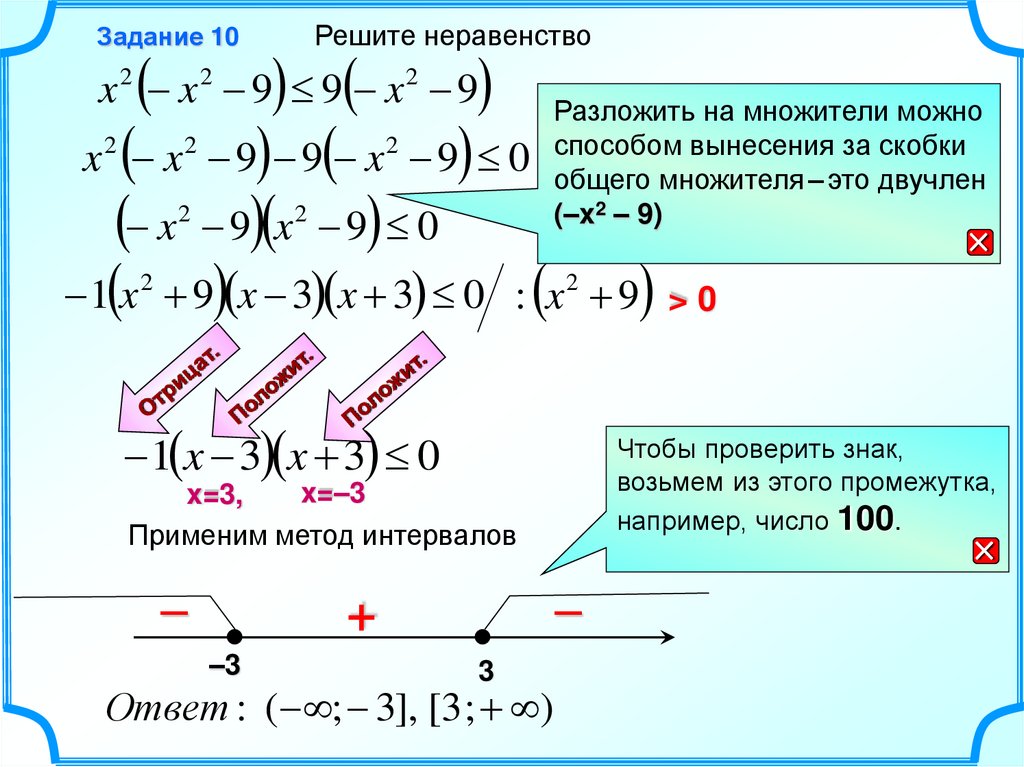
Решите неравенствоЗадание 10
Разложить на множители можно
вынесения за скобки
x x 9 9 x 9 0 способом
общего множителя – это двучлен
(–x – 9)
x 9 x 9 0
1 x 9 x 3 x 3 0 : x 9 > 0
x2 x2 9 9 x2 9
2
2
2
2
2
2
2
2
1 x 3 x 3 0
Чтобы проверить знак,
возьмем из этого промежутка,
например, число 100.
x=–3
x=3,
Применим метод интервалов
–
–
+
–3
3
Ответ : ( ; 3], [3 ; )
14.
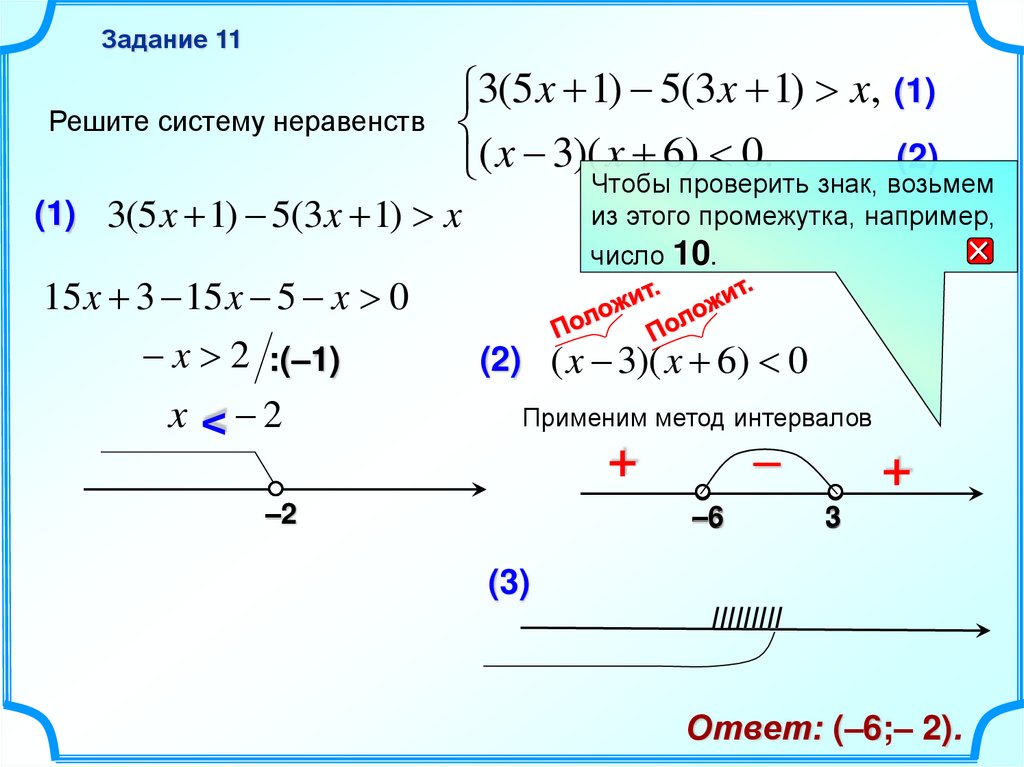
Задание 11Решите систему неравенств
3(5 x 1) 5(3x 1) x, (1)
(2)
( x 3)( x 6) 0.
Чтобы проверить знак, возьмем
из этого промежутка, например,
число 10.
(1) 3(5 x 1) 5(3x 1) x
15 x 3 15 x 5 x 0
x 2 :(–1)
x < 2
(2) ( x 3)( x 6) 0
Применим метод интервалов
–
+
–2
–6
+
3
(3)
IIIIIIIII
Ответ: (–6;– 2).
15.
Задание 1316 x 25 y
Найдите значение выражения
y , если x y 3
4 x 5 y
a2–b2 = (a-b)(a+b)
4 x 2 5 y 2
16 x 25 y
4 x 5 y 4 x 5 y
y
y
4 x 5 y
4 x 5 y
3
4 x 5 y y 4 x 4 y 4 x y
4 3 12
Ответ: 12.
16.
Задание 14.1100 n
2 n 1
n 2
5 4
Сократите дробь
(ab)n = anbn (am)n = amn
4 * 52
n
2 n
2
n
2 n
100
4 5
4 5
2 n 1 n 2
2 n 1
n 2 2 n 1
n
2
5 4
5 4
5 4
4 5 80
2
1
1
2n
4 5
2 n 1
5
2
n–2
на меньшее
Сокращаем наСокращаем
меньшее число:
52n–1 число: 4
Сокращаем,
т.е. делим
Сокращаем, т.е.
делим
n–n+2 = 42
4n : 4n–2
4n–(n–2)
52n : 52n–1 = 52n–(2n-1)
= 5=2n–2n+1
= 5=1 4
Ответ: 80.
17.
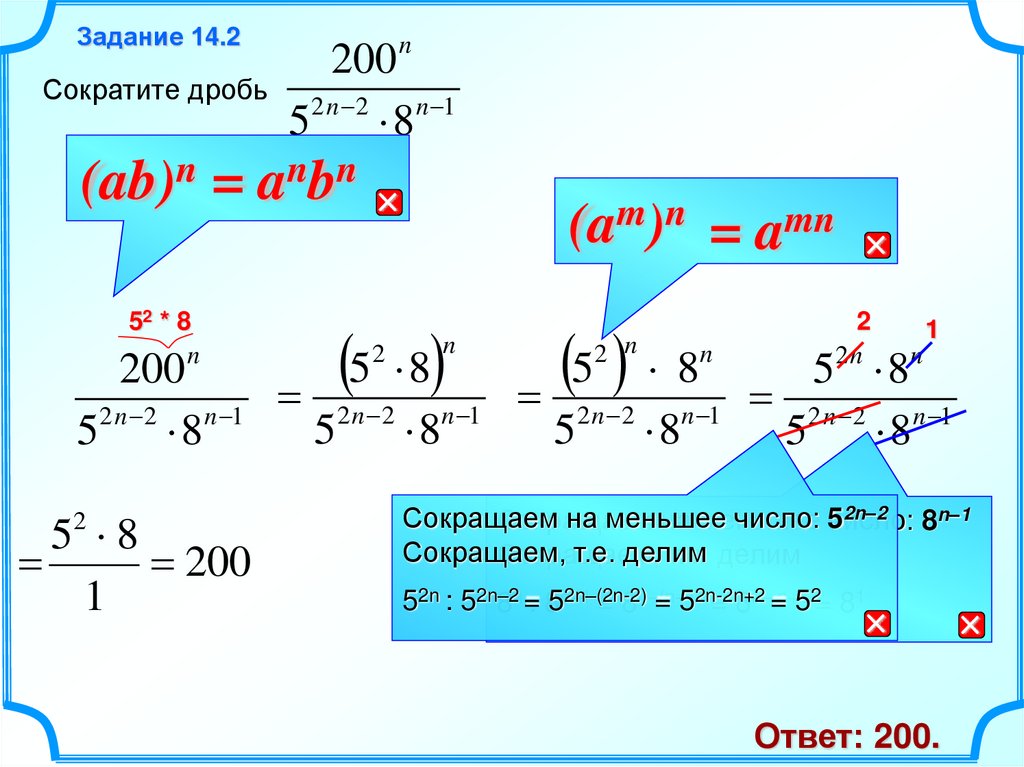
Задание 14.2n
200
Сократите дробь
52 n 2 8n 1
(ab)n = anbn
52 * 8
n
(am)n = amn
n
2 n
2
2n
1
5 8
5 8
200
5 8
2 n 2 n 1 2 n 2 n 1 2 n 2 n 1
2n 2
n 1
5
8
5
8
5
8
5
8
5 8
200
1
2
2
n
n
2n–2
Сокращаем
на меньшее
число: 5
Сокращаем
на меньшее
число:
8n–1
Сокращаем,
т.е. делим
Сокращаем,
т.е. делим
2n–(2n-2)
52n : 52n–2
= 52n-2n+2
52= 81
8n=: 85n–1
= 8n–(n–1)
= 8n–=n+1
Ответ: 200.
18.
65
x
x
Сократите дробь
Задание 14.3
2
9
x 2x
5
(ab)n = anbn ana m = an+m
5 x x
6
2 ( 6 )
4
25 x x
25 x
25 x 25
12,5
9
5
9 5
4
9
5
2
x 2x
2x
2x
x 2x
2
6
2
Ответ: 12,5.
19.
Задание 14.45
4
x
x
Сократите дробь
3
7
x 5x
5
(ab)n = anbn ana m = an+m
4 x x
5
5
3 ( 5 )
2
64 x x
64 x
64 x 64 12,8
7
5
7 5
7
5
x 5x
x 5x
5x
5 x 2 5
3
3
Ответ: 12,8.
20.
Задание 15Найдите значение выражения
p(a)
c(8 c)
, если p(c)
p(8 a)
c 4
ac (8 ac)
p (a
c)
ac 4
(8 a )(8 ( 8 a )) (8 a )(8 8 a )
p(8 a)
8 a 4
8 a 4
(8 a ) a
4 a
2
p(a)
8a a (8 a) a a(8 a) (a 4)
1
:
p(8 a)
a 4
4 a
(a 4) (8 a) a
Ответ: –1.
21.
Задание 16Найдите значение выражения
m(a)
2
1
, если m(b) b 2b
b
b
1
m
a
2
1
m(ab) a
b 2a
b
ab
ab
1 2
1 1
2
1 1
m 2 : 1 : 2 a a
a a
a a
a
a a
2
1
a 2a
a
a
m(a )
1
1
m
a
Ответ: 1.
22.
Задание 17.1если
Найдите значение выражения 31a – 4b + 55
a – 4b + 7
=8
4a – b + 7
Произведение средних членов
пропорции = произведению
крайних членов.
a – 4b + 7
= 8
1
4a –b + 7
a – 4b + 7 = 8(4a –b + 7)
Искомое выражение
31a – 4b + 55 = – 49 + 55 = 6
a – 4b + 7 = 32a – 8b + 56
32a – a – 8b + 4b + 56 – 7 = 0
31a – 4b + 49 = 0
31a – 4b = – 49
Ответ: 6.
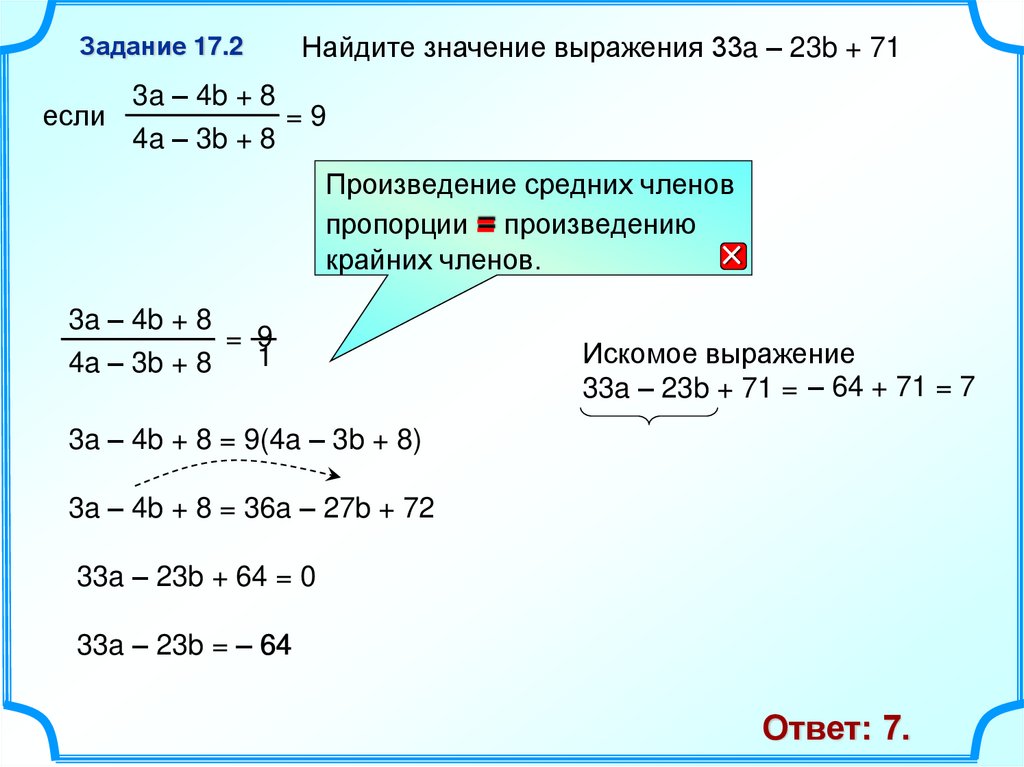
23.
Задание 17.2Найдите значение выражения 33a – 23b + 71
3a – 4b + 8
если
=9
4a – 3b + 8
Произведение средних членов
пропорции = произведению
крайних членов.
3a – 4b + 8
= 9
1
4a – 3b + 8
Искомое выражение
33a – 23b + 71 = – 64 + 71 = 7
3a – 4b + 8 = 9(4a – 3b + 8)
3a – 4b + 8 = 36a – 27b + 72
33a – 23b + 64 = 0
33a – 23b = – 64
Ответ: 7.
24.
Задание 18Найдите
f (5), если f ( x 2) 49 x
x 2 5
x 7
f (5) f (7 2) 49 7 4 2 16
Ответ: 16.
25.
Задание 19Решите уравнение
x 7 36 x 7
3
x 7 36 x 7 0
3
x 7 x 7 36 0
2
x 7 0
x 7
Разложим левую часть на
множители. Вынесем за
скобки общий множитель –
двучлен (x–7)
Разложим
Произведение
левую часть
равно
на множители.
Применим
нулю,формулу
если один из
равен нулю.
2 множителей
2
a – b = (a – b)(a + b)
x 7 36 0
x 7 6 x 7 6 0
2
x 13 x 1 0
x 13
x 1
Ответ: 1; 7; 13.
26.
Задание 20Решите уравнение
x3 – 20x2 = –5x2 – 13х – x3
+
+
+
2
x3 – 20x2 = – 5x –13х –x3 0
2x3 – 15x2 + 13х = 0
х=0
D = b2 – 4ac
–b +
– D
x=
2a
или
х(2x2 – 15x + 13) = 0
2x2 – 15x + 13 = 0
D = b2 – 4ac
a = 2, b = –15, c = 13,
D = (–15)2 – 4 2 13 = 225 – 104 = 121 = 112
–b +
– D
x=
2a
–(–15) + 11 15 + 11 26
= 6,5
x=
=
=
4
4
2 2
x=
–(–15) – 11 15 – 11
4
=
=
=1
4
4
2 2
Ответ: 0; 1; 6,5.
27.
Задание 21.1Решите уравнение
Применим способ группировки для
разложения левой части на
множители.
Обязательно сделайте
самопроверку: раскройте скобки,
получится ли исходное
выражение.
Произведение
C помощью
равно нулю,
самопроверки
если один из множителей
легко находить
свои
равен
ошибки.
нулю.
x3 3x 2 25x 75 0
x ( x 3) 25( x 3) 0
2
( x 3) x 2 25 0
( x 3) x 5 ( x 5) 0
x 3 0
x 5 0
x 5 0
x 3
x 5
x 5
Ответ: –3, 5, –5.
28.
Задание 21.2Решите уравнение
Применим способ группировки
для разложения левой части
на множители
2 x3 8x 2 9 x 36 0
2 x 2 ( x 4) 9( x 4) 0
Произведение равно нулю,
если один из множителей
равен нулю.
y
5
ГОТОВИМСЯ x
К ОГЭ
( x 4) 2 x 2 9 0
2x2 9 0
x 4 0
2 x 2 9
9
2
x
2
x 4
Нет корней
Ответ: 4.
29.
Задание 22Решите уравнение
x 1 x 2 4 x 4 4 x 2 Применим формулу
2+2ab+b2 =(a + b)2
2
a
x 1 x 2 4 x 2
для трёхчлена x +4x+4 = (x+2)
2
x 1 x 2 4 x 2 0
Разложим левую часть на
Вынесем за
x 2 x 1 x 2 4 0 множители.
скобки общий множитель –
x 2 x 2 2 x x 2 4 0 двучлен (x + 2)
2
x 2 x x 6 0
2
x 2 0
x 2
2
Произведение равно нулю, если
один из множителей равен нулю.
1x 2 x 6 0
1 x1 3 ,
x1 x2 квадратное
Это приведённое
(старший
уравнение
x 2
x
x
6
коэффициент
1 2равен 1). 2
Найдем корни по теореме Виета.Ответ: –3; –2; 2.
30.
Задание 23Решите уравнение
x 4 x 5 x 6 x 2 x 5 x 6
x 4 x 5 x 6 x 2 x 5 x 6 0
Разложим левую часть
x 5 x 6 x 4 ( x 2) 0 на множители.
Вынесем за скобки
x 5 x 6 x 4 x 2 0 общий множитель –
это двучлены
(x – 5)(x – 6)
x 5 x 6 ( 2) 0
Произведение равно нулю, если
один из множителей равен нулю.
x 5 0
x 6 0
x 5
x 6
2 0
Ответ: 5; 6.
31.
Задание 24Решите уравнение
Разложим левую часть
на множители.
Вынесем за скобки
общий множитель –
двучлены
(3x – 6)(x – 6)
3x 6 x 6 3x 6 x 6
2
2
3x 6 x 6 3x 6 x 6 0
3x 6 x 6 3x 6 (x 6) 0
3x 6 x 6 3x 6 x 6 0
Произведение равно нулю, если
3x 6 x 6 2x 0
один из множителей равен нулю.
2
2
3x 6 0
x 6 0
2x 0
3x 6
x 2
x 6
x 0
Ответ: 0, 2, 6.
:2
32.
Задание 25Решите уравнение
x x 12
2
4
x x 12 0
2
4
Разложим левую часть на множители.
Применим формулу
a2 – b2 = (a – b)(a + b)
x (x 12) x (x 12) 0
x x 12 x x 12 0
2
2
2
2
x x 12 0
2
D ( 1) 2 4 1 4 0
Произведение равно нулю,
если один из множителей
равен нулю.
x x 12 0
2
x1 x2 1
x1 x2 12
x1 4
x2 3
Ответ: – 4; 3.
33.
Задание 27ОДЗ :
Решите уравнение
2x2 4x 6
1
2
x 9
Применим основное свойство
пропорции: в верной пропорции
произведение средних членов равно
произведению крайних членов.
2x 4x 6
1
2
1
x 9
2
2x2 4x 6 x2 9
1x 4x 3 0
2
x1 x2 4
x1 x2 3
x2 9 0
x 3 x 3 0
x 3 !
Это приведённое квадратное
уравнение (старший
коэффициент равен 1).
Найдем корни по теореме Виета.
x1 1, ОДЗ
x 3 ОДЗ
2
Ответ: – 1.
34.
Задание 28Решите уравнение
x 2x 2 x 2 x 3
2
ОДЗ :
x2 2x 2 x 2 x 3 0
2 x 0
2
x
2x 3 0
1
x 2 : ( 1)
x <2!
Это приведённое квадратное
уравнение (старший
коэффициент равен 1).
Найдем корни по теореме Виета.
x1 x2 2
x1 x2 3
x1 1, ОДЗ
x 3 ОДЗ
2
Ответ: – 1.
35.
Задание 29Решите уравнение
x 25 x 3x 10 0
2
2
2
2
x 2 25 0
2
x 3 x 10 0
(1)
x 2 25 0
x 5 x 5 0
x 5,
(2)
Оба слагаемых в левой части
уравнения неотрицательны,
поэтому их сумма может быть
равна нулю только если они
оба равны нулю. Получаем
систему двух уравнений.
1 x 2 3x 10 0
x 5!
Это приведённое квадратное
уравнение (старший
коэффициент равен 1).
Найдем корни по теореме Виета.
x1 x2 3
x1 x2 10
x1 5!,
x 2.
2
Ответ: –5.
36.
Задание 30 Решите систему уравнений2
способ
(
2
)
4 x 2 y 9, Применим
8
x
2 y 18,
сложения. При сложении
+
2+
уравнений исключится y.
2
8 x y 3.
8 x y 3.
12 x 2 12
:12
x 1
2
x1 1,
3 y 15
y 5
y1 5,
x2 1, y1 5.
Ответ: (1; 5), (–1; 5).
37.
Задание 31 Решите систему уравненийx 3 y 31, ( 2)
2
2 x 6 y 2 31x.
2
2
2 x 2 6 y 2 62,
+
2
2 x 6 y 2 31x.
0 31x 62
31x 62
x1 2,
2
Подставимспособ
Применим
х = 2 в первое
алгебраического
уравнение,
чтобысложения.
найти
Сначала первое
значение
у.
2 уравнение
2
x
3
y
31
умножим на (–2).
x2 3 y 31
2
2
4 3 y 2 31
3 y 2 27
y2 9
: 31
y1 3
y2 3
Ответ: (2; 3), (2;–3).
:3
38.
Задание 32 Решите систему уравнений4 x 3 2 7 y, Вычтем из уравнения (1)
уравнение (2)
–
3x 4 2 7 y.
2
2
4 x 3 3x 4 0
Подставим x=1 в
первое уравнение
4 1 3 7 y
2
7 y 49
y 7
4x 3 3x 4 4x 3 (3x 4) 0
Подставим x=–1 в
первое уравнение
7 x 7 4x 3 3x 4 0
2
7 x 1 x 1 0
4 ( 1) 3 7 y
2
x1 1, 1
4 3 7 y
x2 1,
7y 1
2
1
Ответ: (1; 7), (–1; 7 )
1
у =7
39.
Задание 33Заметим, что правые части
Решите систему уравнений
равны, приравняем левые
части
2
Теперь подставим «х» во 2
5 х у 6 у,
2
5 х у 6 х. 2
6 у 6х : 6
уравнение вместо «у». Получим:
5 х х 6 х
2
6 х 6 х
2
36 х 6 х
у х
2
36 х 6 х 0
6 х(6 х 1) 0
6х 1 0
6х 0 : 6
6х 1 : 6
х 0; у 0
1
1
х ; у
Ответ: (0; 0); ( 1 ; 1 ).
6 6
6
6
2
40.
Задание 342
2
x у 5,
xy 2. 2
Решите систему уравнений
Используем способ
алгебраического сложения.
x у 5,
+
2
xy
4
2
2
x 2 2 xy у 2 9,
x у 2 9,
xy 2
x у 3,
xy 2
x у 3,
xy 2
(1; 2), (2;1)
(–1; –2), (–2;–1)
Ответ: (1; 2), (2;1), (–1;–2), (–2;–1).
41.
Задание 35 Решите систему уравненийПрименим способ
Подставим
х=2
–4ввпервое
первое
алгебраического
уравнение,
чтобысложения.
найти
Сначала первое
значение
у.
уравнение
2
умножим наx(–1).
2 y 1
( 1)
x 2 y 1,
2
x 15 2 y y 2 .
2
x 2 2 y 1,
+
2
x 15 2 y y 2 .
2
15 y 1
y 16
2
y 1
x 2 y4 1 x 2 (-4)
2
2
x 9
2
x1 3
x 7
2
x2 3
y1 4,
y2 4,
Ответ: (4; 3), (4;–3).



































 Математика
Математика








