Неравенства

1.

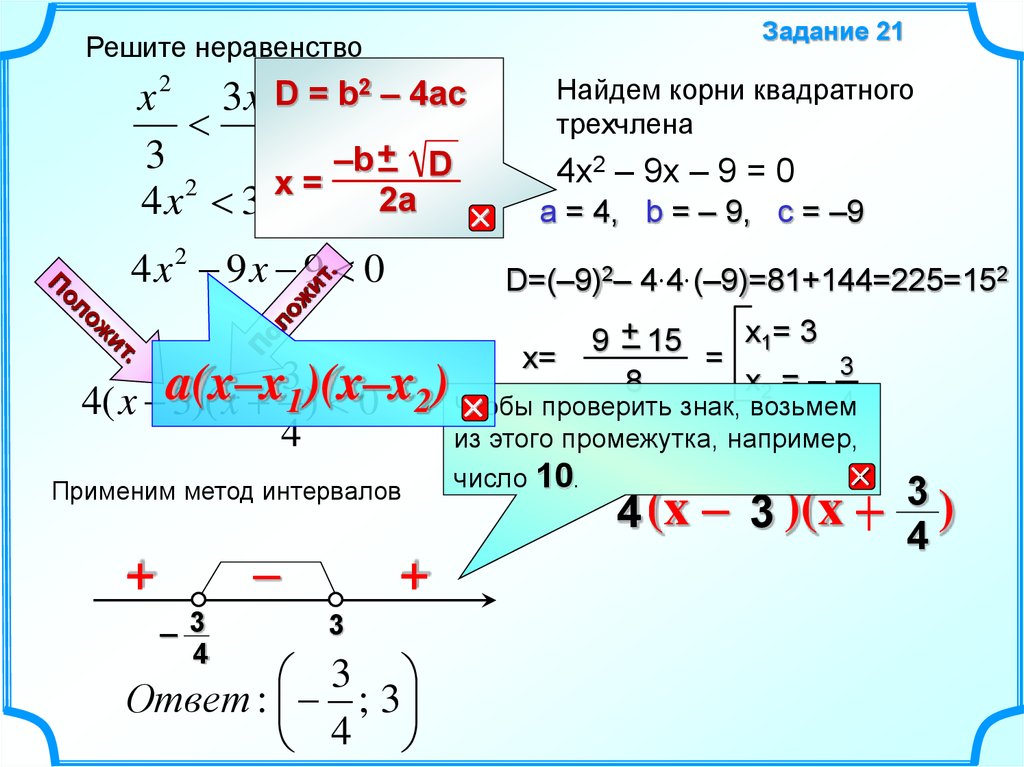
Задание 21
Решите неравенство
x 2 3x D3= b2 – 4ac
12
4 –b +– D
3
4 x 2 3(x3x= 3)2a
4x2 9x 9 0
Найдем корни квадратного
трехчлена
4x2 – 9x – 9 = 0
a = 4, b = – 9, c = –9
D=(–9)2– 4 4 (–9)=81+144=225=152
x=
9+
– 15 = x1= 3
x2 = – 3
8
3 )(x–x )
a(x–x
4( x 3)( x 1) 0 2 Чтобы
проверить знак, возьмем4
4
Применим метод интервалов
–
+
–3
4
+
3
3
Ответ : ; 3
4
из этого промежутка, например,
число 10.
4a(x – x31)(x –
3
x42)

2.

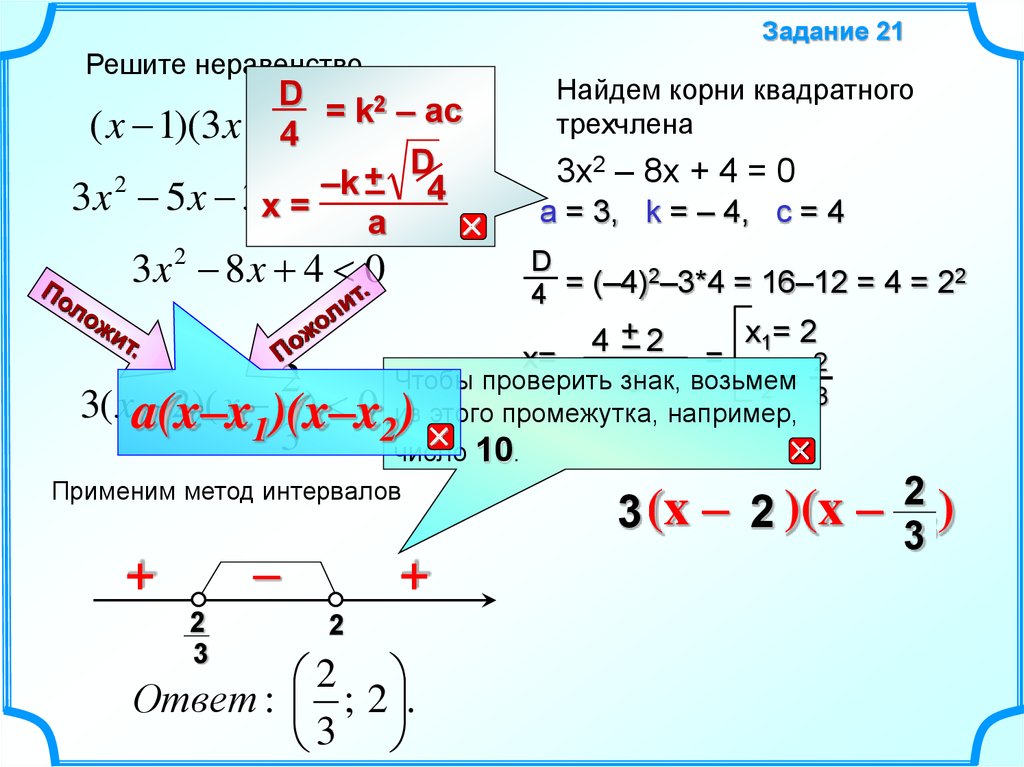
Задание 21
Решите неравенство
D = k2 – ac
( x 1)(3x 54) 1
D
+
2
3x 5 x 3xx = 5–k –1 40
a
3x 2 8 x 4 0
Найдем корни квадратного
трехчлена
3x2 – 8x + 4 = 0
a = 3, k = – 4, c = 4
D
2–3*4 = 16–12 = 4 = 22
=
(–4)
4
x1= 2
4+
2
–
x=
=
2
Чтобы проверить знак,
возьмем
x
=
3
2
3
2
3( xa(x–x
2)( x )(x–x
) 0 из
этого промежутка, например,
13
2)
число 10.
Применим метод интервалов
–
+
2
3
+
2
2
Ответ : ; 2 .
3
3a(x – x21)(x –
2
x32)

3.

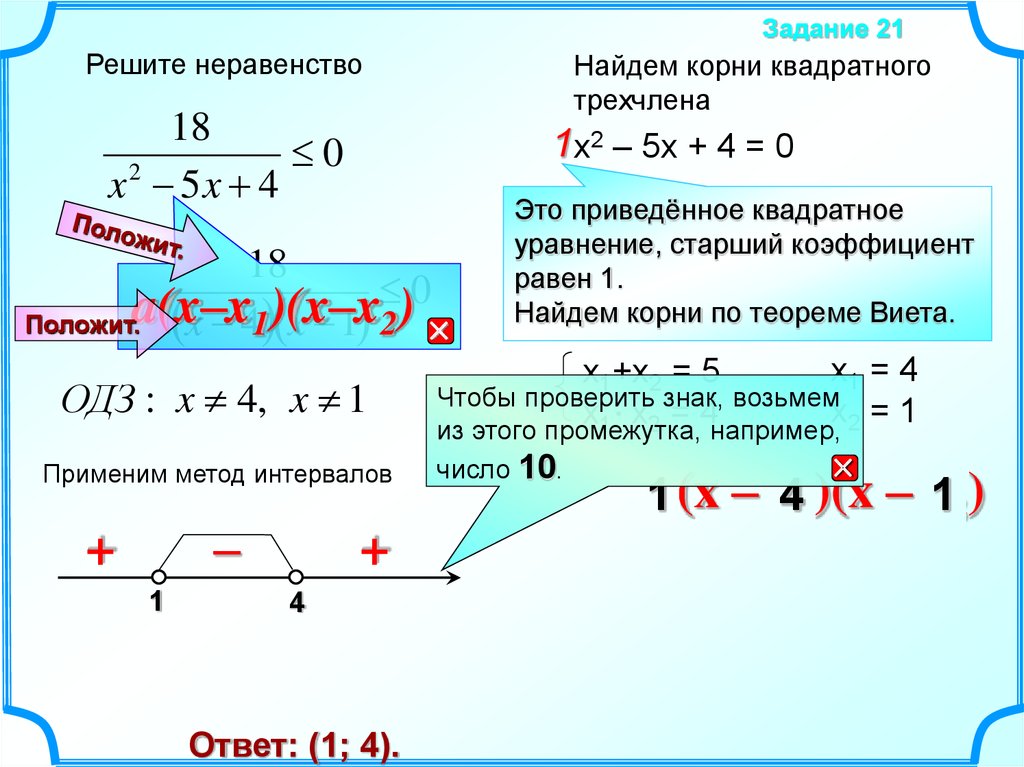
Задание 21
Решите неравенство
Найдем корни квадратного
трехчлена
18
0
2
x 5x 4
1x2 – 5x + 4 = 0
18
)0
a(x–x
)(x–x
Положит. x 41 x 1 2
ОДЗ : x 4, x 1
Применим метод интервалов
–
+
1
+
4
Ответ: (1; 4).
Это приведённое квадратное
уравнение, старший коэффициент
равен 1.
Найдем корни по теореме Виета.
x1 = 4
x1+x2 = 5
Чтобы проверить знак, возьмем
x1 x2 = 4например,x2 = 1
из этого промежутка,
число 10.
1a(x – x41)(x – x12)

4.

Задание 21
Решите неравенство
Найдем корни квадратного
трехчлена
18
0
2
x 4 x 21
x2 – 4x – 21 = 0
18
)0
a(x–x
)(x–x
Положит. x 71
x 3 2
ОДЗ : x 7, x 3
Это приведенное квадратное
уравнение, a = 1. Можно
применить теорему Виета.
Чтобы проверить
x1 =
x1 + x2знак,
= 4 возьмем
из этого промежутка, например,
x2 =
x1 x2 = – 21
число 10.
Применим метод интервалов
–
–
+
–3
7
Ответ : ( ; 3); (7; )
7
–3
1a(x – x71)(x – x32)

5.

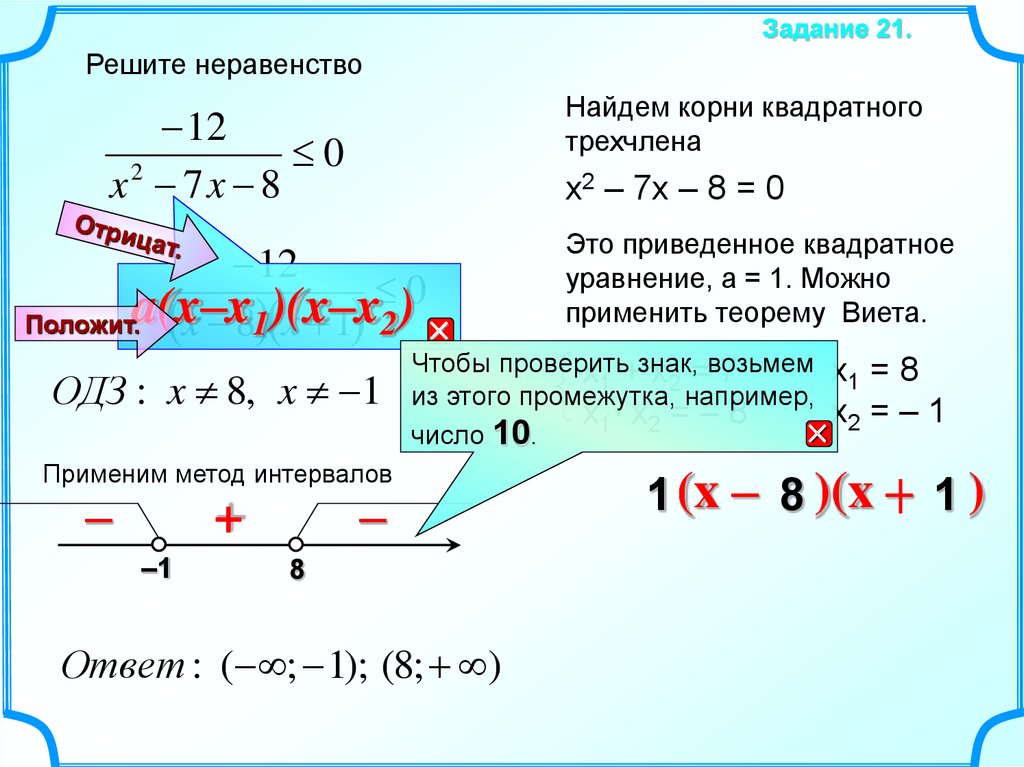
Задание 21.
Решите неравенство
Найдем корни квадратного
трехчлена
12
0
2
x 7x 8
x2 – 7x – 8 = 0
12
)0
a(x–x
)(x–x
Положит. x 81
x 1 2
ОДЗ : x 8, x 1
Чтобы проверить
x1
x1 +знак,
x2 =возьмем
7
из этого промежутка, например,
x2
x1 x2 = – 8
число 10.
Применим метод интервалов
–
–
+
–1
Это приведенное квадратное
уравнение, a = 1. Можно
применить теорему Виета.
8
Ответ : ( ; 1); (8; )
=8
=–1
1a(x – x81)(x – x12)

6.

Задание 21.
Решите неравенство
22
0
2
x 2 x 35
Т .к. числитель 22 0,
2
1
ОДЗ : x 7, x 5
x 7 x 5 0
Чтобы проверить
возьмемx
x1 + xзнак,
1
2 = 2
из этого промежутка, например,
x2
x1 x2 = –35
число 10.
Применим метод интервалов
–
+
–5
x2 – 2x – 35 = 0
Это приведенное квадратное
уравнение, a = 1. Можно
применить теорему Виета.
то a(x–x
x 2 x )(x–x
35 0)
2
Найдем корни квадратного
трехчлена
+
7
Ответ : ( ; 5); (7; )
=7
= –5
1a(x – x71)(x – x52)

7.

Задание 21 Решите неравенство
x 3 x 1 0
x2 4x 3
0,
4
6
x x
x 1 x
4
2
a(x–x1)(x–x2) x 3 x 1
ОДЗ :
x 0,
x 1 . !
x 1 x 1 x
4
0
x 3 1 x
0
4
x 1 x 1 x
Найдем корни квадратного
трехчлена
x2 – 4x + 3 = 0
Это приведенное квадратное
уравнение, a = 1. Можно
применить теорему Виета.
x1 + x2 = 4
x1 x2 = 3
x1 = 3
x2 = 1
1a(x – x31)(x – x12)
x 3
0 Чтобы проверить знак, возьмем
4
из этого промежутка, например,
x
1
x
0
–1
число 10.
При
переходе
через
«0»
Проверьте все ли условия из ОДЗ учтены!
знак не меняется!
Ответ :
+
–
–
+
( ; 1); [3; )
3
Применим метод
интервалов
Положит.
–1
0 1
3

8.

Задание 21
19
Решите неравенство
0
2
x 5 6
19
Разложить на множители
0
знаменатель можно по формуле
x 5 2 ( 66 )2
19
0
x 5 6 x 5 6
a2 – b2 =(a – b)(a+b)
ОДЗ : x 5 6 , x 5 6
Применим метод интервалов
–
–
+
–5– 6
Чтобы проверить знак,
возьмем из этого промежутка,
например, число 100.
–5+ 6
Ответ : ( 5 6 ; 5 6 )

9.

Задание 21
15
Решите неравенство
0
2
x 1 3 Разложить на множители
15
0
знаменатель можно по формуле
2
2
x 1 ( 33 )
a2 – b2 =(a – b)(a+b)
15
0
x 1 3 x 1 3
ОДЗ : x 1 3 , x 1 3
Применим метод интервалов
–
–
+
–1– 3
Чтобы проверить знак,
возьмем из этого промежутка,
например, число 100.
–1+ 3
Ответ : ( 1 3; 1 3 )

10.

x 5
2
Решите неравенство
x 5
2
3 x 5 0
x 5 x 5
x=5
3 x 5
Разложить на множители можно
способом вынесения за скобки
общего множителя – это двучлен
(x – 5)
3 0
x 5 0
x 5
x=5+ 3
–
5
+
5+ 3
Ответ : [5; 5 3 ]
x 5 3 0
x 5 3
Чтобы проверить знак,
возьмем из этого промежутка,
например, число 100.
Применим метод интервалов
+
Задание 21

11.

x 7
2
Решите неравенство
x 7
2
11 x 7 0
x 7 x 7
x=7
11 x 7
Разложить на множители можно
способом вынесения за скобки
общего множителя – это двучлен
(x – 7)
11 0
x=7+ 11
Чтобы проверить знак,
возьмем из этого промежутка,
например, число 100.
Применим метод интервалов
–
+
7
Задание 21
+
7+ 11
Ответ : (7; 7 11)

12.

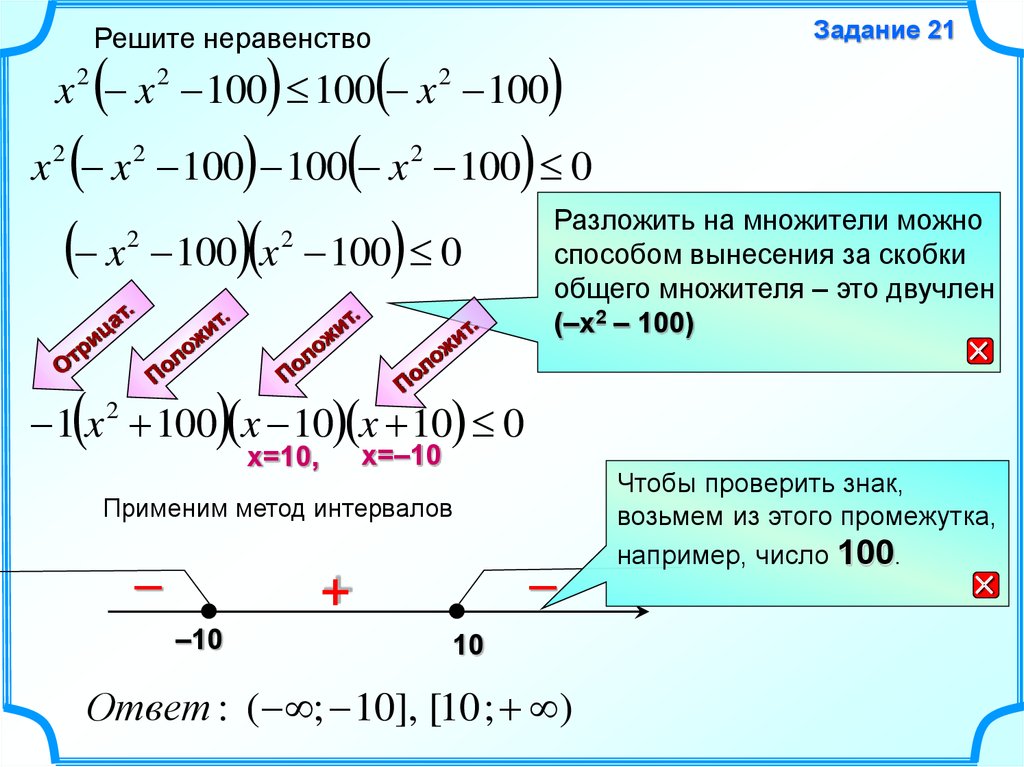
Решите неравенство
x 2 x 2 100 100 x 2 100
x
100 x
Задание 21
x 2 x 2 100 100 x 2 100 0
2
2
100 0
Разложить на множители можно
способом вынесения за скобки
общего множителя – это двучлен
(–x2 – 100)
x=10,
1 x 2 100 x 10 x 10 0
x=–10
Применим метод интервалов
–
–
+
–10
10
Ответ : ( ; 10], [10 ; )
Чтобы проверить знак,
возьмем из этого промежутка,
например, число 100.

13.

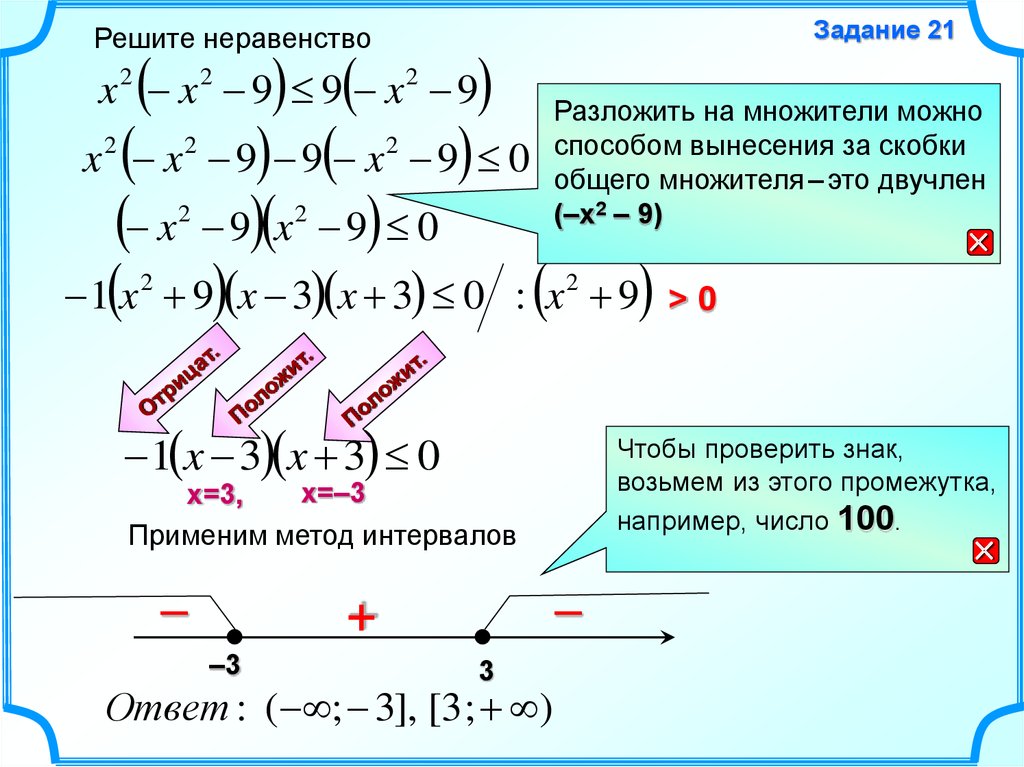
Задание 21
Решите неравенство
Разложить на множители можно
вынесения за скобки
x x 9 9 x 9 0 способом
общего множителя – это двучлен
(–x – 9)
x 9 x 9 0
1 x 9 x 3 x 3 0 : x 9 > 0
x2 x2 9 9 x2 9
2
2
2
2
2
2
2
2
1 x 3 x 3 0
Чтобы проверить знак,
возьмем из этого промежутка,
например, число 100.
x=–3
x=3,
Применим метод интервалов
–
–
+
–3
3
Ответ : ( ; 3], [3 ; )

14.

Задание 21
Решите неравенство
4x + 3x – 7 = 0
4x 3x 2 x 7D =2b –x 4ac
–b +
4x 3x 2 x 7x =2 x–2a D 0 a = 4, b = 3, c = –7
Разложить
на множители
можно
D=3
–4 4 (-7)=9+112=
вынесения за скобки
=121=11
2 x 4x 3x 7 0 способом
общего множителя – это двучлен
2
2
2
2
2
2
2
2
2
2
2
(–2– x2)
a(x–x1)(x–x2)
1 2 x 4 x 1,75 x 1 0
2
x=–1,75;
x=1
Применим метод интервалов
–
–1,75
–
+
1
Ответ : 1,75;1
2
–3 +
– 11 =
x=
2 4
3
14
7
x1= – = – 4 = –1 4
8
=
8
x2 = 8 = 1
Чтобы проверить знак,
возьмем из этого промежутка,
например, число 100.

15.

Задание 21
Решите неравенство
x3 2 x 2 4 x 8 0
Разложить на множители можно
способом вынесения за скобки
общего множителя – это двучлен
(x + 2)
x 2 ( x 2) 4( x 2) 0
x 2 x 2 4 0
x 2 x 2 x 2 0
x 2 x 2 0
2
Нули функции: x= –2,
Применим метод интервалов.
Рассмотрим функцию y=(х+2)2(х–2)
При переходе через «–2»
знак не меняется!
–
–
–2
Чтобы проверить знак,
возьмем из этого промежутка,
например, число 100.
x= 2
+
2
Ответ : { 2}, [2 ; )

16.

Найдите область определения выражения
Задание 21
1
1 2x x
2
1 2x x2 0
(1 2 x x 2 ) 0
Применим формулу
a2–2ab+b2 =(a–b)2
(1 x) 2 0 ( 1)
(1 x) 2 0
Нет решений
Ответ: нет решений.

17.

Задание 21.
Найдите наименьшее целое число, входящее в
область определения выражения
25 ( х 2)
2
( х 2) 2 25
Применим формулу
a2–b2 =(a–b)(a+b)
25 ( х 2) 0
2
5 ( х 2) 5 ( х 2) 0
5 х 2 5 х 2 0
3 х 7 х 0
–
–
+
–7
Чтобы проверить знак,
возьмем из этого промежутка,
например, число 100.
3
[–7; 3]
Ответ: –7.

18.

Найдите сумму целых отрицательных решений
неравенства
Задание 21
ОДЗ : x 4
x 2 5 x 18
2
x 4
x 5 x 18 2 x 8
0
x 4
2
a(x–x1)(x–x2)
x 2 7 x 10
0
x 4
–5
( x 2)( 5x 5)
0
( x5 4)
x–4
x 5 x 18
2 0
1
x 4
2
–2
4
–
+
–5 - 4 - 3 –2
–
5+
4
Чтобы
проверить знак,
2
1 xвозьмем
+ 7x +10
= 0 промежутка,
из этого
Это приведённое квадратное
например, число 5.
уравнение (старший
x ( 5;равен
2) 1).(4; )
коэффициент
Найдем корни по теореме Виета.
x1+х2 =–7
x1 х2 = 10
4 ( 3) 7
х1=–5
х2=–2
Ответ: –7.

19.

ОДЗ : x 4
2
х 1 1
0
4 x 4
2
2
1
х 1
4
4 xформулу
Применим
Решите неравенство
Задание 21.
4–x
2
a2–b2 =(a–b)(a+b)
2
3
4–x
х 1 1 х 1 1
0
4 x 2 4 x 2
2 х 2 4 x 2 х 2 4 x
0
2 4 x 2 4 x
3х 2 х 6 0
–6
–
+
–6
+
2
3
4
3х 2 х 6 0 22 4 x 2 > 0
2
2
2 4 x
Ответ: [–6; 2 ].
3