Похожие презентации:
Общие сведения о колебаниях. Тема 1
1. ФИЗИКА 0702907mts - Сайт «Физика» dist.donntu.org
ВОЛКОВАЛЕКСАНДР ФЁДОРОВИЧ
Профессор кафедры физики
Тел. 071 334 94 73
e-mail: afv.volkov@yandex.ru
1
2. ФИЗИКА
• 1. Лекции – один раз в неделю, здесь, вэтой аудитории.
• 2. Лабораторные работы – один раз в
неделю, кафедра физики.
• График выполнения лабораторных
работ смотри на сайте (или на стенде
кафедры)
• 3. Индивидуальные домашние задания
на сайте.
2
3. Домашнее задание
• Прочитать: Учебник, том 2• §§ 1- 3 Гармонические колебания (ГК).
• § 4 Энергия гармонических колебаний.
• Задачник, т. 2.
• Сделать задачи 23, 24 (стр. 173).
Образец решения смотри на сайте.
3
4. 2-й семестр КОЛЕБАНИЯ И ВОЛНЫ
Глава 1. Колебания• Колебаниями называются процессы
повторяющиеся во времени.
• Колебания называются
периодическими, если значения
физических величин, изменяющихся в
процессе колебания, повторяются
через равные промежутки времени.
4
5. §1 Общие сведения о колебаниях
• Система, совершающая колебания,называется колебательной
системой или осциллятором.
• Различают колебания:
• свободные (собственные);
• затухающие;
• вынужденные;
• автоколебания.
5
6. § 2 Гармонические колебания
• Гармонические колебания – этопроцессы, при которых изменение
физических величин с течением
времени происходит по закону синуса
или косинуса:
x t A cos t 0
• мы будем считать, что колеблющаяся
величина изменяется по закону косинуса.
6
7. График гармонического колебания
78. Характеристики колебаний
• Мгновенное значение колеблющейсявеличины
(t) (буква – кси)
t x t x t T
• Это значение физической величины
(смещения, угла отклонения, заряда,
напряжения, тока) в заданный момент
времени.
8
9. Характеристики колебаний
• Амплитуда колебаний (А) –максимальное значение колеблющейся
величины.
• Амплитуда – положительная величина.
A= Xmax
• Период колебаний (Т) – время одного
полного колебания.
• Единица измерения [ T ] = с (секунда)
9
10. Характеристики колебаний
• Частота колебаний ( ) – числоколебаний за единицу времени.
1
• Связь периода и частоты
T
• Единица измерения [ ] =1/ c = Гц (герц
• Угловая или циклическая частота
(ω) – число колебаний за 2π секунд
2
2
Т
10
11. Характеристики колебаний
• Фаза колебаний (φ) – величина,определяющая мгновенное состояние
колебательной системы:
t t 0
• где φ0 – начальная фаза (значение
фазы при t = 0).
• Единица измерения [ φ ] = рад (радиан).
11
12. Гармонические колебания
• Уравнение, описывающеегармонические колебания можно
записать так:
2
x t A cos t 0
T
• мы будем считать, что колеблющаяся
величина изменяется по закону косинуса.
12
13. График гармонического колебания (косинусоида)
1314. Гармонические колебания
• Гармонические колебания скалярнойвеличины определяются в целом тремя
независимыми постоянными
параметрами: частотой (периодом),
амплитудой и начальной фазой.
• Амплитуда колебаний и начальная
фаза определяются начальными
условиями, а частота и период –
свойствами колебательной системы.
14
15. 2.2 Дифференциальное уравнение гармонических колебаний (ДУГК)
• Дифференциа́льное уравне́ние — этоуравнение, в которое входят
производные функции, (может входить
и сама функция), независимая
переменная и параметры.
d
2
0
0
2
dt
2
15
16. Дифференциальное уравнение гармонических колебаний
• Представляет собой линейноеоднородное дифференциальное
уравнение второго порядка.
• Дифференцирование ведётся по
времени t - (независимая переменная).
16
17. Дифференциальное уравнение гармонических колебаний
• Решением такого дифференциальногоуравнения является функция
t A cos 0t 0
17
18. Дифференциальное уравнение гармонических колебаний
• Вывод: Если при анализе физическихпроцессов той или иной природы,
сделанных на основе законов и
приближений, возникает уравнение
подобного вида, то это означает, что
рассмотренная система может
совершать гармонические колебания.
• Частота (период) колебаний будет
определяться свойствами самой
18
системы.
19. лекционные демонстрации
• Посмотрим лекционныедемонстрации:
• Маятник запись колебаний песком
1.37
• Синусоида на осциллографе 1.58
19
20. .
§3 Примеры систем,совершающих
гармонические
колебания
20
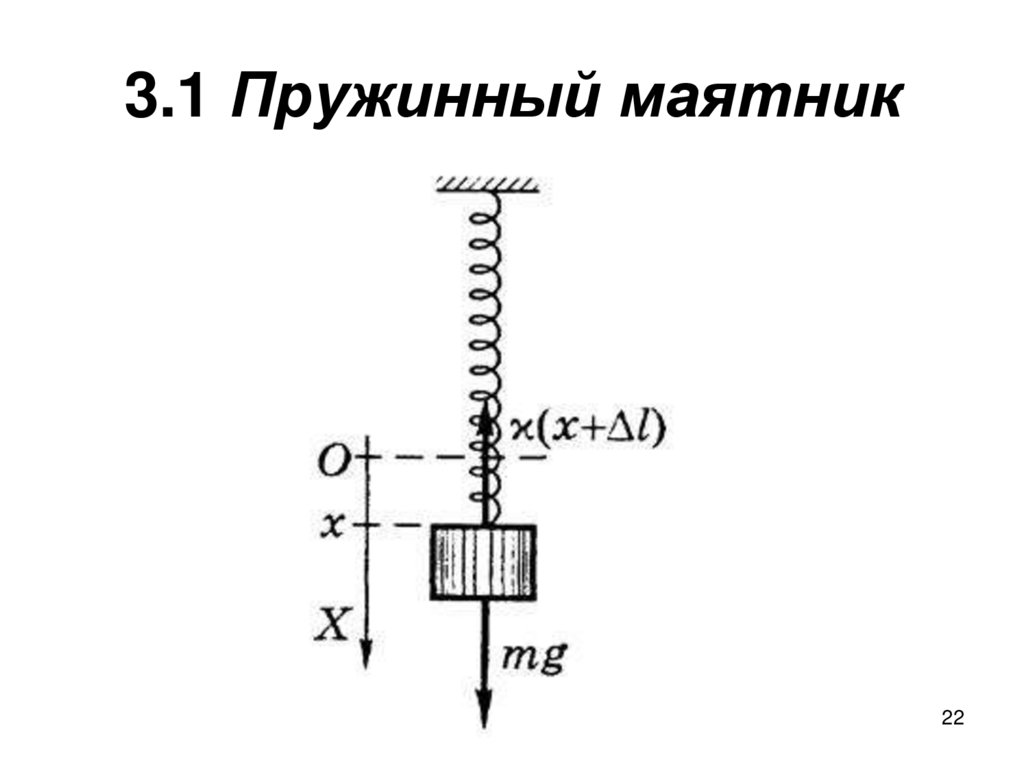
21. 3.1 Пружинный маятник
• Пружинный маятник – тело массойm, подвешенное на абсолютно упругой
пружине жёсткостью k и совершающее
колебания под действием силы
упругости.
21
22. 3.1 Пружинный маятник
2223. Пружинный маятник
2d x
kx m 2
dt
23
24. 3.1 Пружинный маятник
• Движение грузика описываетсяуравнением
2
d x k
x
0
2
m
dt
• движение шарика под действием
упругой силы описывается ДУГК.
k
2
0
m
24
25. 3.1 Пружинный маятник
• Общее решение уравнения имеет вид:x t A cos 0t 0
• Период колебаний пружинного
маятника:
2
m
T
2
0
k
25
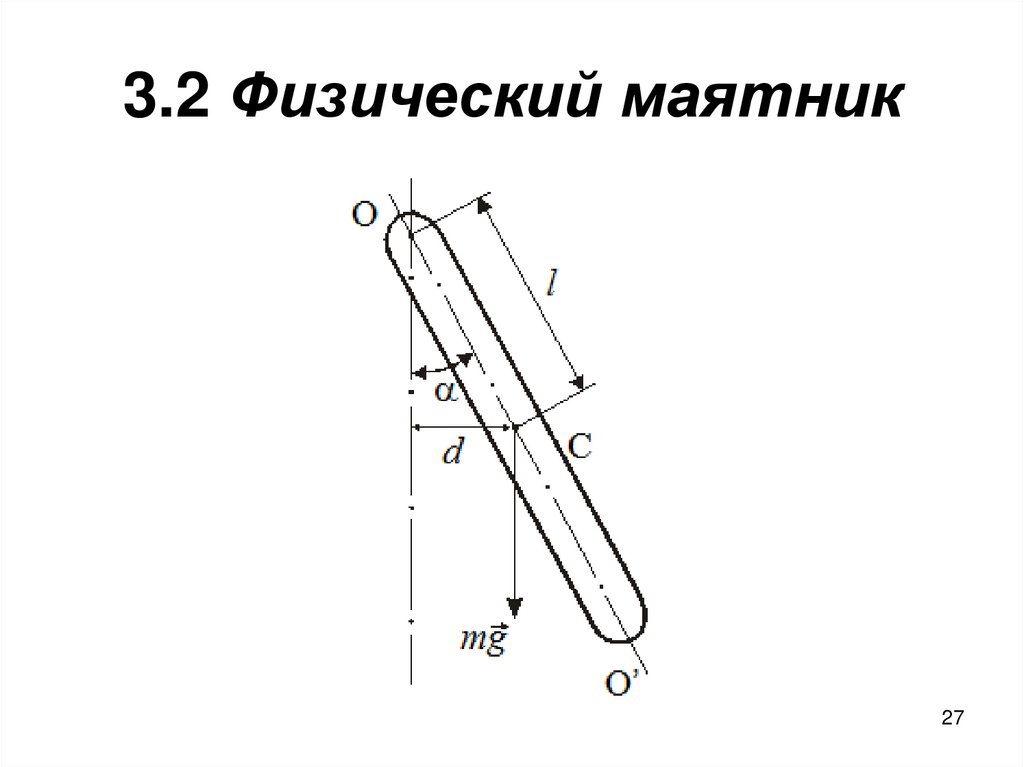
26. 3.2 Физический маятник
• Физический маятник – твёрдое тело,совершающее колебания под
действием силы тяжести относительно
неподвижной горизонтальной оси, не
проходящей через центр масс.
26
27. 3.2 Физический маятник
2728. 3.2 Физический маятник
• Возникает вращающий момент М,который стремится вернуть маятник в
положение равновесия:
M mgl sin
• Используя закон динамики
вращательного движения, получим
d mgl
sin
0
2
J
dt
2
28
29. 3.2 Физический маятник
• Это уравнение похоже на ДУГК, ноздесь sin !
• Уравнение является нелинейным
дифференциальным уравнением
второго порядка.
• Колебания, описываемые этим
уравнением, не будут гармоническими.
• НО! при малых углах sin
29
30. 3.2 Физический маятник
• В этом случае уравнение можнопривести к виду:
d mgl
0
2
J
dt
2
• Обозначив
mgl
02
J
• Получим ДУГК.
30
31. 3.2 Физический маятник
• Следовательно, малые колебанияфизического маятника являются
гармоническими.
• Период гармонических колебаний
физического маятника
2
J
T
2
0
mgl
31
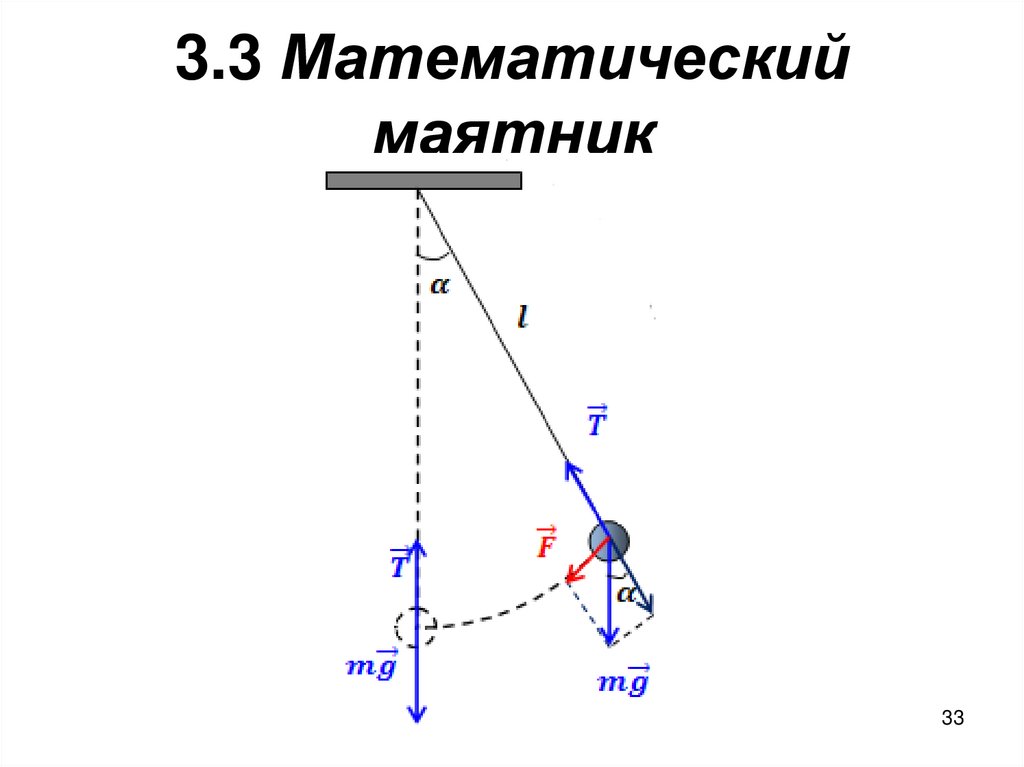
32. 3.3 Математический маятник
• Математический маятник –материальная точка, подвешенная на
невесомой нерастяжимой нити и
совершающая колебания в
вертикальной плоскости под действием
силы тяжести.
• Математический маятник можно рассматривать как
предельный случай физического маятника, масса
которого сосредоточена в одной точке.
32
33. 3.3 Математический маятник
3334. 3.3 Математический маятник
• Период колебаний математическогомаятника
l
T 2
g
34
35. Посмотрим лекционную демонстрацию
• Грузы на пружинах 3.52.• Физический маятник 2.46
• Математический маятник 4.27.
35
36. 3.4 Колебательный контур
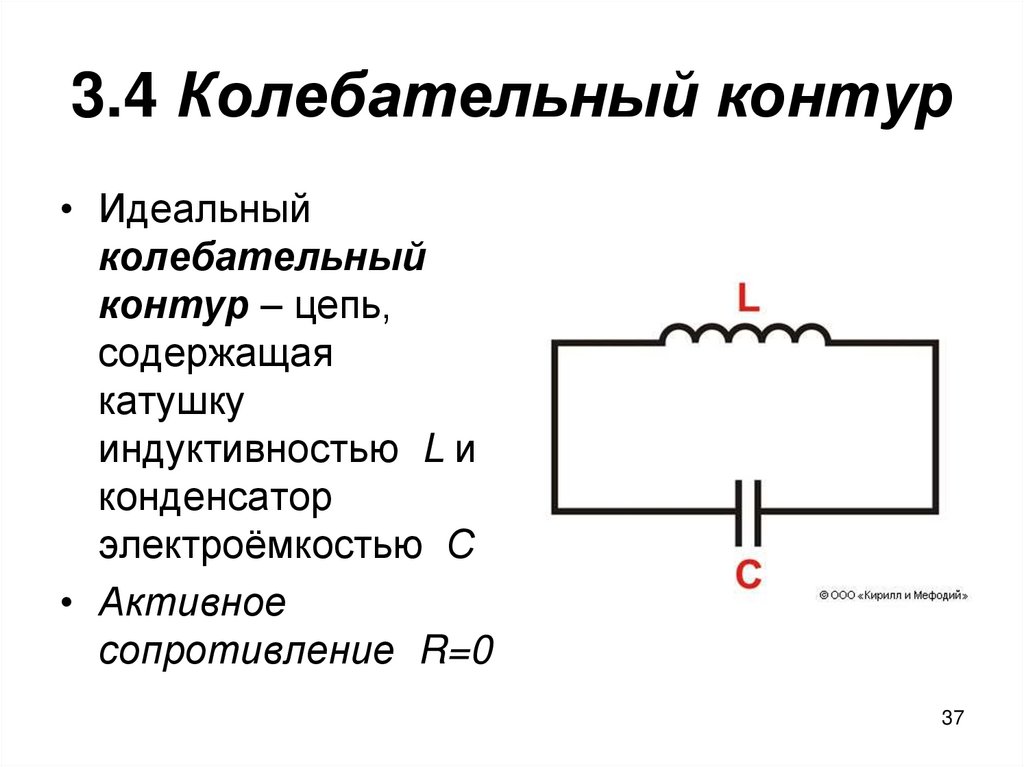
3637. 3.4 Колебательный контур
• Идеальныйколебательный
контур – цепь,
содержащая
катушку
индуктивностью L и
конденсатор
электроёмкостью С
• Активное
сопротивление R=0
37
38. Работа колебательного контура
3839. Колебательный контур
• Активное сопротивление R = 0, поэтомуполная энергия не расходуется на
нагревание проводов и остается
величиной постоянной
Wэл + Wмаг = const
2
2
q
Li
const
2C
2
39
40. Колебательный контур
• После преобразований получаемуравнение, которое является ДУГК
2
d q
1
q
0
2
LC
dt
1
2
• где
0 - собственная частота
LC
колебаний
40
41. Колебательный контур
• Решением этого уравнения являетсяфункция
q t qmax cos 0t 0
• Вывод: заряд на обкладках
конденсатора изменяется по
гармоническому закону.
41
42. Колебательный контур
• где qmax максимальное (амплитудное)значение заряда.
• Для периода колебаний получается
формула, которая называется
формулой Томсона
2
T
2 LC
0
42
43. Колебательный контур
• Также в колебательном контуре погармоническому закону изменяются
напряжение на конденсаторе
U t U max cos 0t 0
• И ток в катушке
i t I max cos 0t 0
2
43
44. Давайте подумаем!
• Как изменятся период и собственнаячастота колебаний колебательного
контура, если:
• 1) между обкладками воздушного
конденсатора контура ввести
диэлектрик;
• 2) в катушку ввести сердечник из
парамагнетика?
3) в катушку ввести сердечник из
ферромагнетика?
44
45. Давайте подумаем!
• Совпадают ли фазы колебанийнапряжения на обкладках
конденсатора и тока в идеальном
колебательном контуре?
• Если не совпадают, то каков сдвиг фаз?
45
46. §4 Энергия колебаний
• Характер изменения энергии напримере колебаний пружинного
маятника.
• Потенциальная энергия гармонического
колебания
2
2
kx
kA
2
Wп
cos 0t 0
2
2
46
47. §4 Энергия колебаний
• Кинетическая энергия гармоническогоколебания
2
mv
Wк
2
2 2
mA 0
2
sin 0t 0
2
• Полная энергия гармонического
колебания равна
2
kA
W Wп Wк
2
47
48. §4 Энергия колебаний
• Полная энергия гармоническогоколебания остается величиной
постоянной.
2
• Отметим, что полная энергия W ~ A
пропорциональна квадрату амплитуды.
• Аналогичные периодические превращения
энергии происходят и в колебательном
контуре. Энергия электрического поля
превращается в энергию магнитного поля и
наоборот.
48














































 Физика
Физика