Похожие презентации:
Гармонический осциллятор
1.
Динамика поступательногоФедеральное
агентстводвижения
по образованию
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
Институт цветных металлов и золота
Авторы: доценты кафедры физики, к.ф-м.н. Вершинина Н.И.,
к.т.н. Машукова А.Е.
ОПОРНЫЙ КОНСПЕКТ
по курсу физики
Тема: Гармонический осциллятор
Тема: Гармонический осциллятор
27.11.18
2.
Динамика поступательного движенияСодержание
5. Колебания
Колебания
5.
5.1. Механические
Механические
5.1.
5.2.Электромагнитные
Электромагнитные
5.2.
Тема: Гармонический27.11.18
осциллятор
2
3.
Динамика поступательного движенияСодержание
Введение. Виды колебаний
1. Математический маятник
2. Пружинный маятник
3. Скорость, ускорение, энергия
колеблющейся точки
4. Физический маятник
5. Колебательный контур
6. Гармонический осциллятор
Тема: Гармонический27.11.18
осциллятор
3
4. Виды колебаний
Динамика поступательногодвижения
Введение
Виды колебаний
Всякий периодически повторяющийся во
времени процесс называется КОЛЕБАНИЕМ.
Колебания
Механическ
ие
Электромагн
ит-ные
Свободные незатухающие
Затухающие
Вынужденные
4
Тема: Гармонический осциллятор
5. 1. Математический маятник
Динамикапоступательного движения
Математический
маятник
1. Математический маятник
Тема: Гармонический осциллятор
6. Вывод уравнения колебания
Динамикапоступательного движения
Математический
маятник
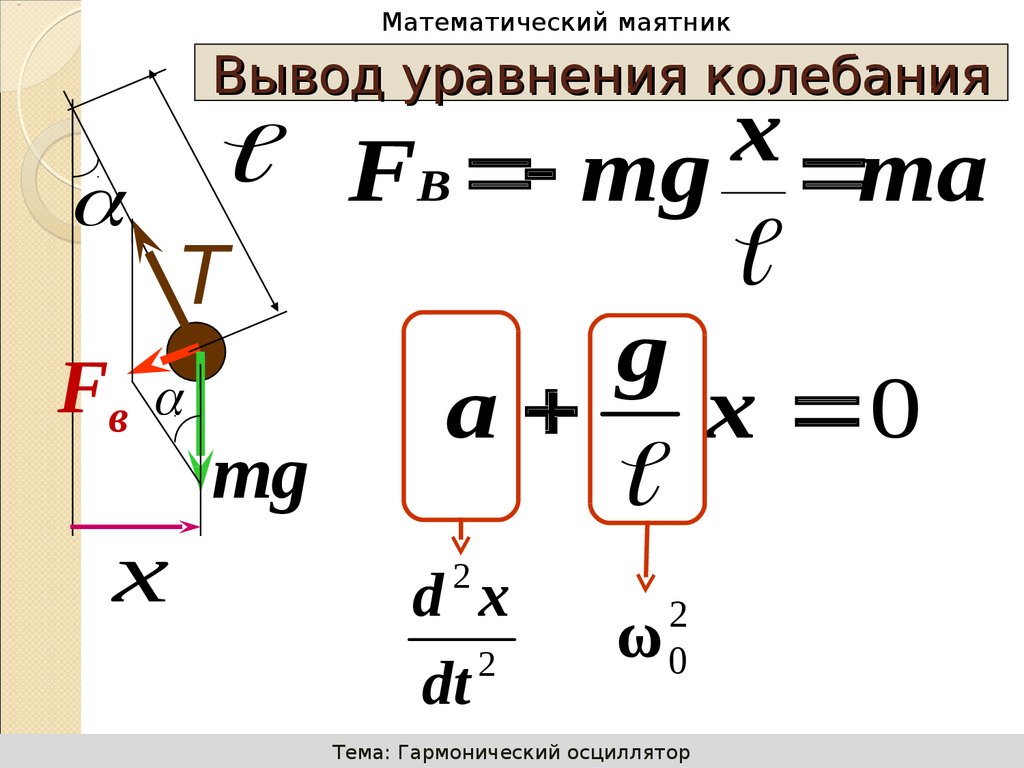
Вывод уравнения колебания
Fв
Т
x
mg
Fв- возвращающая сила
FB mg sin
x
sinα
- смещение точки от положения
равновесия
Тема: Гармонический осциллятор
7. Вывод уравнения колебания
Динамикапоступательного движения
Математический
маятник
Вывод уравнения колебания
FB mg x ma
Fв
Т
x
mg
g
a x 0
2
d x
2
dt
ω
2
0
Тема: Гармонический осциллятор
8. Дифференциальное уравнение колебаний
Динамикапоступательного движения
Математический
маятник
Дифференциальное уравнение
колебаний
22
d x
22
ω
x
0
00
22
dt
(1)
Тема: Гармонический осциллятор
9. Период колебаний
Динамикапоступательного движения
Математический
маятник
Период колебаний
2π
T 2 π
g
ω0
Тема: Гармонический осциллятор
10. Решение дифференциального уравнения:
Динамикапоступательного движения
Математический
маятник
2. Пружинный маятник
0
Тема: Гармонический осциллятор
x
11. 2. Пружинный маятник
ДинамикаПружинныйпоступательного движения
маятник
2. Пружинный маятник
0
x
F= ma = -kx
2
d x k x 0
2
2
dt
m
0
Тема: Гармонический осциллятор
12. 2. Пружинный маятник
ДинамикаПружинныйпоступательного движения
маятник
Дифференциальное уравнение
k 2
0
m
d 2 x 2 x 0
0
2
dt
Период
колебаний
(2)
m
T 2
k
Тема: Гармонический осциллятор
13. Дифференциальное уравнение
ДинамикаПружинныйпоступательного движения
маятник
Решение дифференциального
уравнения
x A sin( ω 0 t α );
Для (1)
и (2)
или
x A cos( ω 0 t α 0 )
А - амплитуда
смещения
0 90
ВОЗЬМЕМ 2-е УРАВНЕНИЕ И НАЙДЕМ
СКОРОСТЬ, УСКОРЕНИЕ И
ВОЗВРАЩАЮЩУЮ СИЛУ
Тема: Гармонический осциллятор
0
14. Решение дифференциального уравнения
3. Скоростьколеблющейся
Скорость, ускорение, энергия точки
точки
Динамика поступательного движения
dx
υ A 0 sin( 0 t 0 )
dt
υmax–
АМПЛИТУДА СКОРОСТИ
Амплитуда – это
максимальное значение
колеблющегося параметра
Тема: Гармонический осциллятор
15. 3. Скорость колеблющейся точки
Динамика поступательногодвижения
Скорость,
ускорение,
энергия точки
Ускорение колеблющейся точки
dυ
2
a A 0 cos( 0 t 0 )
dt
а – амплитуда ускорения
max
Тема: Гармонический осциллятор
16. Ускорение колеблющейся точки
Динамика поступательногодвижения
Скорость,
ускорение,
энергия точки
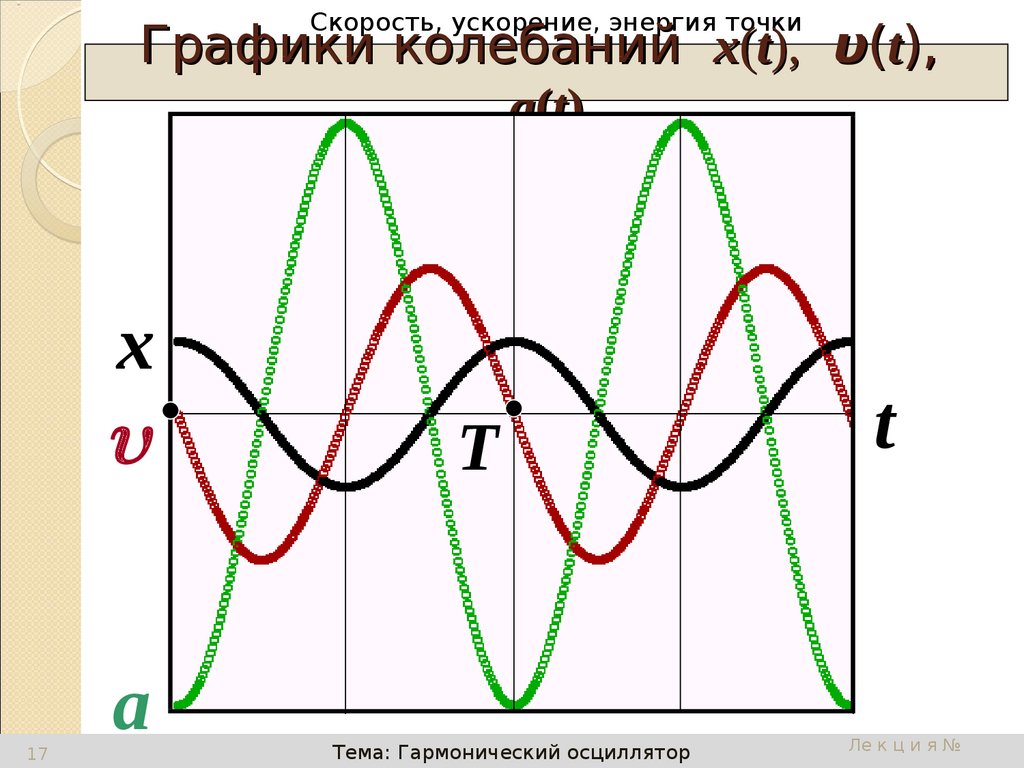
Графики колебаний х(t), υ(t),
a(t)
x
17
a
T
Тема: Гармонический осциллятор
t
Ле к ц и я №
17. Графики колебаний х(t), υ(t), a(t)
Динамика поступательногодвижения
Скорость,
ускорение,
энергия точки
Возвращающая сила
2
0
F ma m A cos( 0 t 0 )
Fmax –
амплитуда силы
Тема: Гармонический осциллятор
18. Возвращающая сила
Динамика поступательногодвижения
Скорость,
ускорение,
энергия точки
Энергия колеблющейся точки
потенциальная
2
2
0
2
mω x
kx
Wп
2
2
1
2 2
2
m ω 0 A сos (ω 0 t α 0 )
2
Тема: Гармонический осциллятор
19. Энергия колеблющейся точки
Динамика поступательногодвижения
Скорость,
ускорение,
энергия точки
Энергия колеблющейся точки
кинетическая
2
mυ
Wк
2
1
2
2
2
mA ω 0 sin (ω 0 t α 0 )
2
Тема: Гармонический осциллятор
20. Энергия колеблющейся точки
Динамика поступательногодвижения
Скорость,
ускорение,
энергия точки
Полная энергия
2
0
mω A
W Wк Wп
2
W Wк ,max Wп ,max
Тема: Гармонический осциллятор
2
21. Энергия
Динамика поступательногодвижения
Скорость,
ускорение,
энергия точки
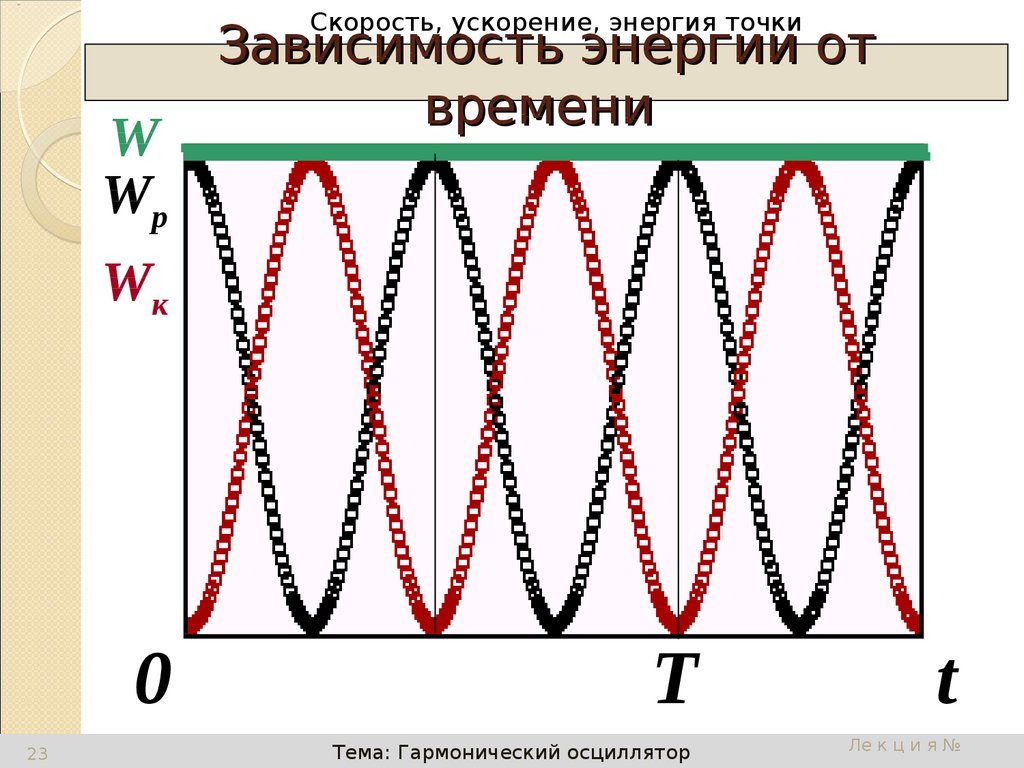
W
Wp
Зависимость энергии от
времени
Wк
0
23
T
Тема: Гармонический осциллятор
t
Ле к ц и я №
22. Полная энергия
Динамикапоступательного движения
Математический
маятник
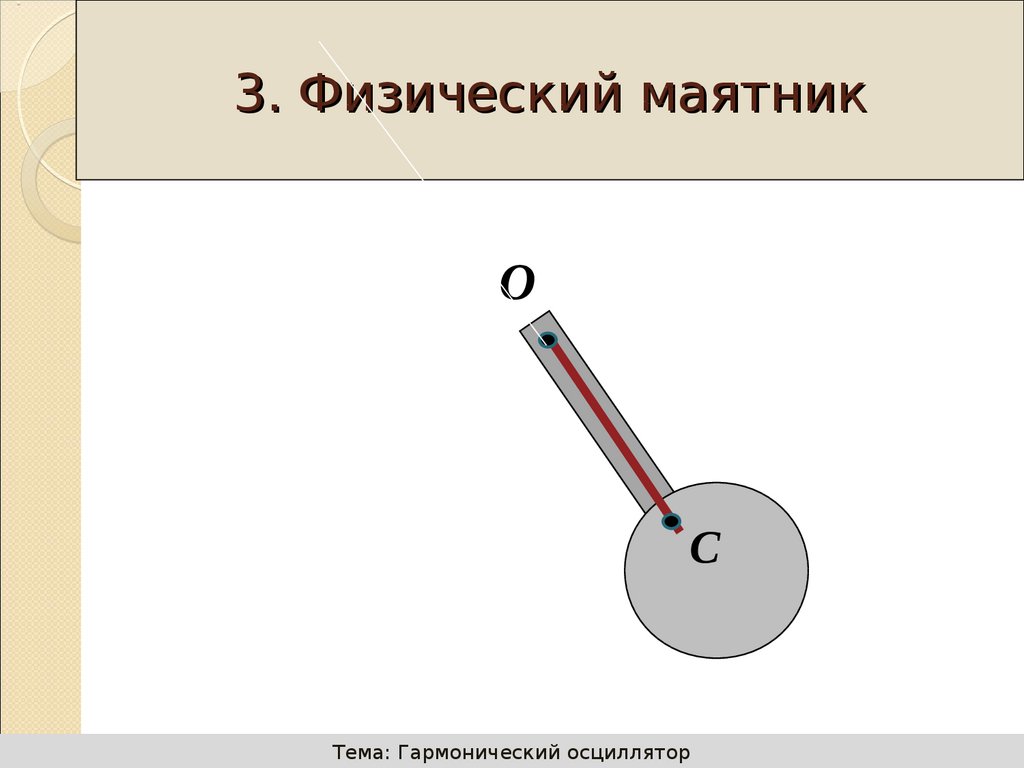
3. Физический маятник
О
С
Тема: Гармонический осциллятор
23. Зависимость энергии от времени
Динамика поступательногодвижения
Скорость,
ускорение,
энергия точки
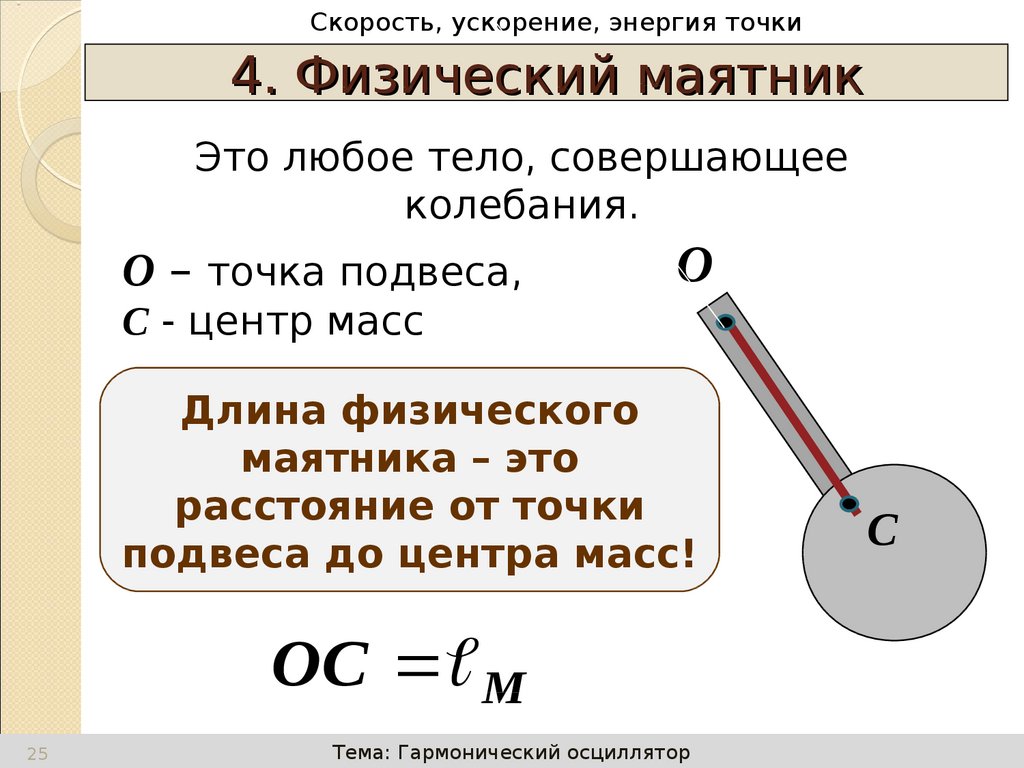
4. Физический маятник
Это любое тело, совершающее
колебания.
О – точка подвеса,
О
С - центр масс
Длина физического
маятника – это
расстояние от точки
подвеса до центра масс!
OC M
25
Тема: Гармонический осциллятор
С
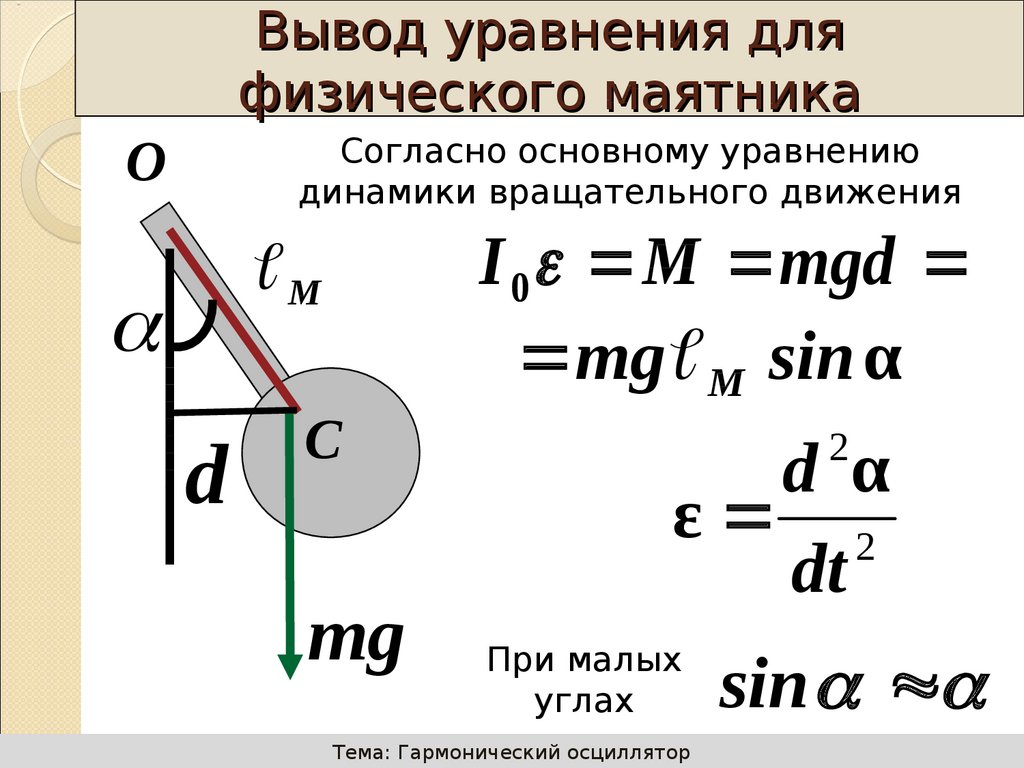
24. 3. Физический маятник
Вывод уравнения дляфизического маятника
Динамика
поступательного движения
Физический
маятник
О
Согласно основному уравнению
динамики вращательного движения
I 0 M mgd
mg M sin α
M
d
С
mg
2
d α
ε 2
dt
При малых
углах
Тема: Гармонический осциллятор
sin
25. 4. Физический маятник
Динамикапоступательного движения
Физический
маятник
Дифференциальное уравнение
2
2
d
mg MM
d mg
0
0
2
2
dt
II00
dt
или
22
d α
22
ω
α
0
00
22
dt
Тема: Гармонический осциллятор
26. Вывод уравнения для физического маятника
Динамикапоступательного движения
Физический
маятник
Частота, период, приведенная
длина
mg M
0
I0
Приведенная
длина
физического
маятника – это
длина
математического
маятника с таким
же периодом
I0
T 2π
m M g
I0
пр
m M
Тема: Гармонический осциллятор
27. Дифференциальное уравнение
Динамикапоступательного движения
Физический
маятник
Приведенная длина
физического маятника
По теореме
Штейнера
2
I 0 I c m M
Ic
пр
M M
m M
Приведенная длина всегда больше
длины физического маятника
Тема: Гармонический осциллятор
28. Частота, период, приведенная длина
Вывод:Динамика
поступательного движения
Физический
маятник
1. Дифференциальные
уравнения и их решения имеют
одинаковый вид для всех
маятников:
2
2
d x
d x
2
2
x
0
x
0
0
0
2
2
dt
dt
22
dd αα
22
ω
α
0
ω
α
0
00
22
dt
dt
2.
Циклическая
частота (и
период)
зависит от
параметров
колебательн
ой системы
Тема: Гармонический осциллятор
29. Приведенная длина физического маятника
Динамикапоступательного движения
Колебательный
контур
4. Колебательный контур
Тема: Гармонический осциллятор
30. Вывод:
5. Колебательный контурДинамика
поступательного движения
Электромагнитные
колебания
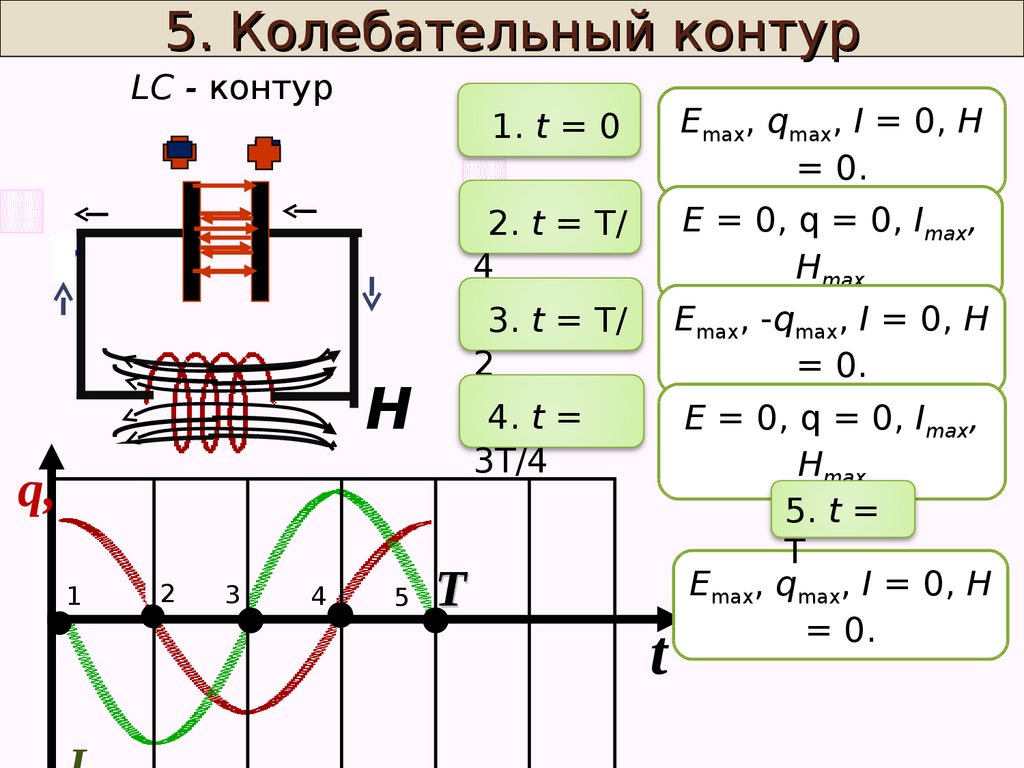
LC - контур
H
q,
1
2
3
4
5
Т
1. t = 0
Еmax, qmax, I = 0, H
= 0.
2. t = T/
4
Е = 0, q = 0, Imax,
Hmax
3. t = T/
2
Еmax, -qmax, I = 0, H
= 0.
4. t =
3T/4
Е = 0, q = 0, Imax,
Hmax
5. t =
Т
Еmax, qmax, I = 0, H
= 0.
t
Тема: Гармонический осциллятор
31. 4. Колебательный контур
Динамикапоступательного движения
Электромагнитные
колебания
По второму правилу Кирхгофа
Напряжение на
конденсаторе
ЭДС
самоиндукции
U c q / C ;
U c c ;
dI
s L
dt
q / C L dI
Тема: Гармонический осциллятор
dt
32. 5. Колебательный контур
Динамикапоступательного движения
Электромагнитные
колебания
Дифференциальное уравнение
2
d q
1
q
0
2
LC
dt
ω0
2
1
ω0
LC
Тема: Гармонический осциллятор
33. 5. Колебательный контур
Динамикапоступательного движения
Электромагнитные
колебания
Дифференциальное уравнение
свободных незатухающих
электромагнитных колебаний
2
d q
2
o q 0
2
dt
Тема: Гармонический осциллятор
34. 5. Колебательный контур
Динамикапоступательного движения
Электромагнитные
колебания
Период колебаний
T 2 LC
Формула Томсона-Кельвина
Тема: Гармонический осциллятор
35. 5. Колебательный контур
Динамикапоступательного движения
Электромагнитные
колебания
Решение дифференциального
уравнения
q qm cos( 0 t 0 )
- амплитуда заряда
Уравнение колебаний силы тока
I qm ω 0 sin( ω 0 t α 0 )
Im
- амплитуда тока
Тема: Гармонический осциллятор
36. 5. Колебательный контур
Динамикапоступательного движения
Электромагнитные
колебания
Уравнение колебаний
напряжения на конденсаторе
qm
U C cos( 0 t 0 )
C
- амплитуда
напряжения на
конденсаторе
Тема: Гармонический осциллятор
37. По второму правилу Кирхгофа
Динамикапоступательного движения
Электромагнитные
колебания
Энергия электрического и
магнитного полей
2
q
LI
WE ; WM
2C
2
2
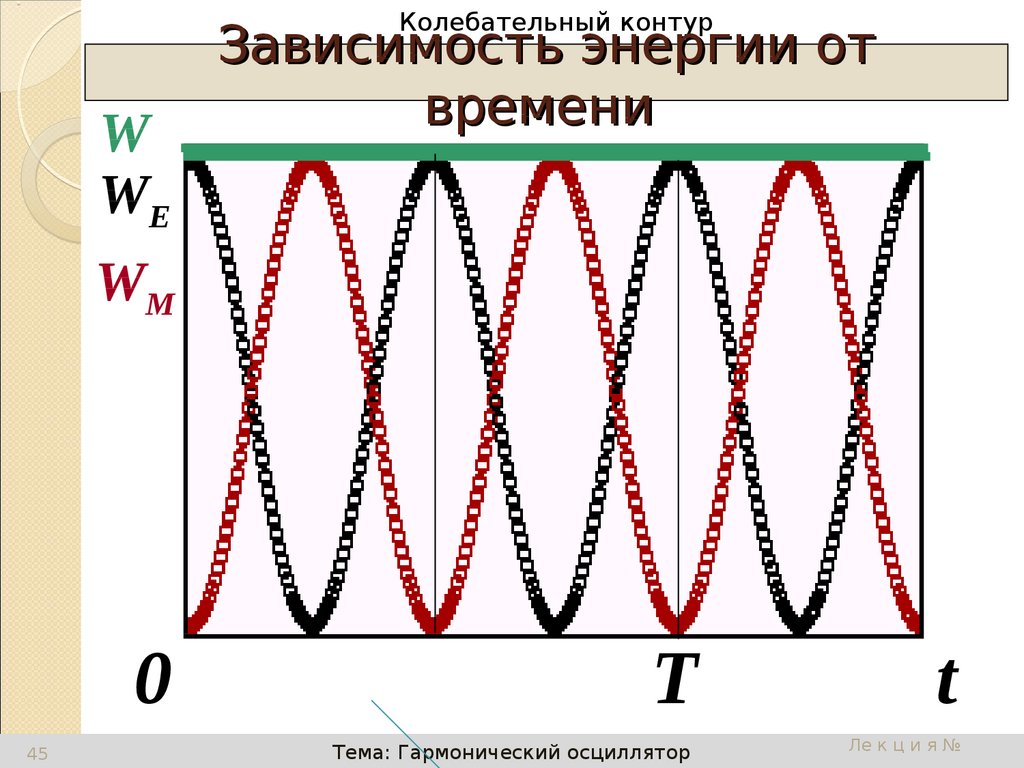
Когда одна из энергий максимальна,
другая равна нулю – происходит
переход энергии электрического поля
в энергию магнитного и наоборот.
Тема: Гармонический осциллятор
38. Дифференциальное уравнение
Динамикапоступательного движения
Электромагнитные
колебания
Полная энергия
W W E W M
22
m
m
22
m
m
q
LI
W
2C
2
Полная энергия остается
постоянной во времени (LC контур – идеальный)
Тема: Гармонический осциллятор
39. Дифференциальное уравнение свободных незатухающих электромагнитных колебаний
Динамикапоступательного движения
Колебательный
контур
W
WE
Зависимость энергии от
времени
WM
0
45
T
Тема: Гармонический осциллятор
t
Ле к ц и я №
40. Период колебаний
Динамикапоступательного движения
Гармонический
осциллятор
6. Гармонический осциллятор
Это система, совершающая
колебания, описываемые
уравнением вида
2
S
2
ω0 S 0
2
t
Тема: Гармонический осциллятор
(1)
41. Решение дифференциального уравнения
Динамикапоступательного движения
Гармонический
осциллятор
Примеры гармонического
осциллятора
1. Пружинный
маятник
2. Математический
маятник
3. Физический
маятник
4. Колебательный
контур
Тема: Гармонический осциллятор
42. Уравнение колебаний напряжения на конденсаторе
Динамикапоступательного движения
Гармонический
осциллятор
Уравнение гармонического
осциллятора
S S m с os(ω0 t α 0 )
ил
иS
(2)
S m sin(ω0 t α )
S - колеблющийся параметр
(x, υ, a, q, I, Uc , B, H, E и т. д.);
Sm=A - амплитуда колебаний
Тема: Гармонический осциллятор
43. Энергия электрического и магнитного полей
Динамикапоступательного движения
Гармонический
осциллятор
График колебаний
S
T
Sm
t
0
S S m cos(ω o t α 0 ) ; α 0 0
Тема: Гармонический осциллятор
44. Полная энергия
Динамикапоступательного движения
Гармонический
осциллятор
Основные параметры
(ω 0 t α 0 )
- фаза
колебаний;
Ед. изм. -радианы или градусы
α 0 (α )
- начальная
фаза;
- собственная
ω 0 циклическая
2
частота колебаний,
т.е.
число колебаний
Ед. изм. 1/cза
секунд
Тема: Гармонический осциллятор
45. Зависимость энергии от времени
Динамикапоступательного движения
Гармонический
осциллятор
ν
Частота и период колебаний
- частота колебаний, изм.
в герцах (Гц).
ω 0 2πν
Т - период колебаний - время
полного колебания.
Измеряется в секундах.
2π
1
T
ω0
ν
Тема: Гармонический осциллятор
46. 6. Гармонический осциллятор
Динамикапоступательного движения
Гармонический
осциллятор
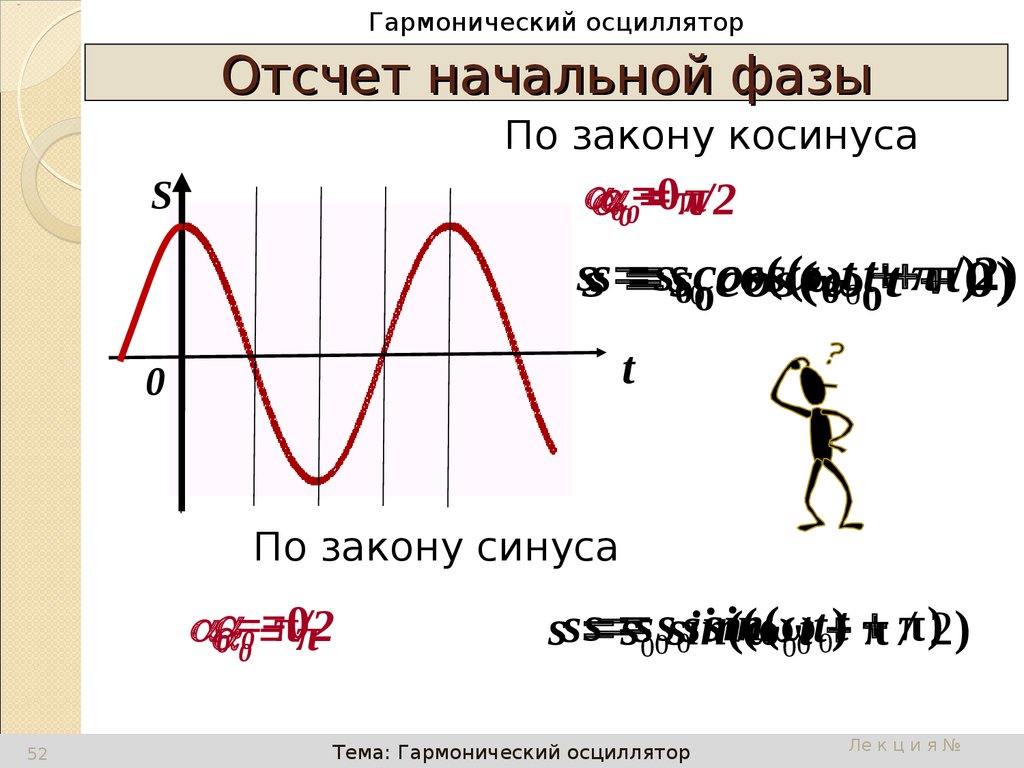
Отсчет начальной фазы
По закону косинуса
000=0
π
== π/2
S
sss
(
ω
t
π
/
2)
sss00cos
cos
(
ω
t
π
)
cos
(
ω
t
0)
0
0
0
0
t
0
По закону синуса
=0
π/2
0
=
π
0=
0
52
s
sin
(ω
t )t π)
ss
ss00ssin
((ωω
0sin
00t 0 π / 2)
Тема: Гармонический осциллятор
Ле к ц и я №















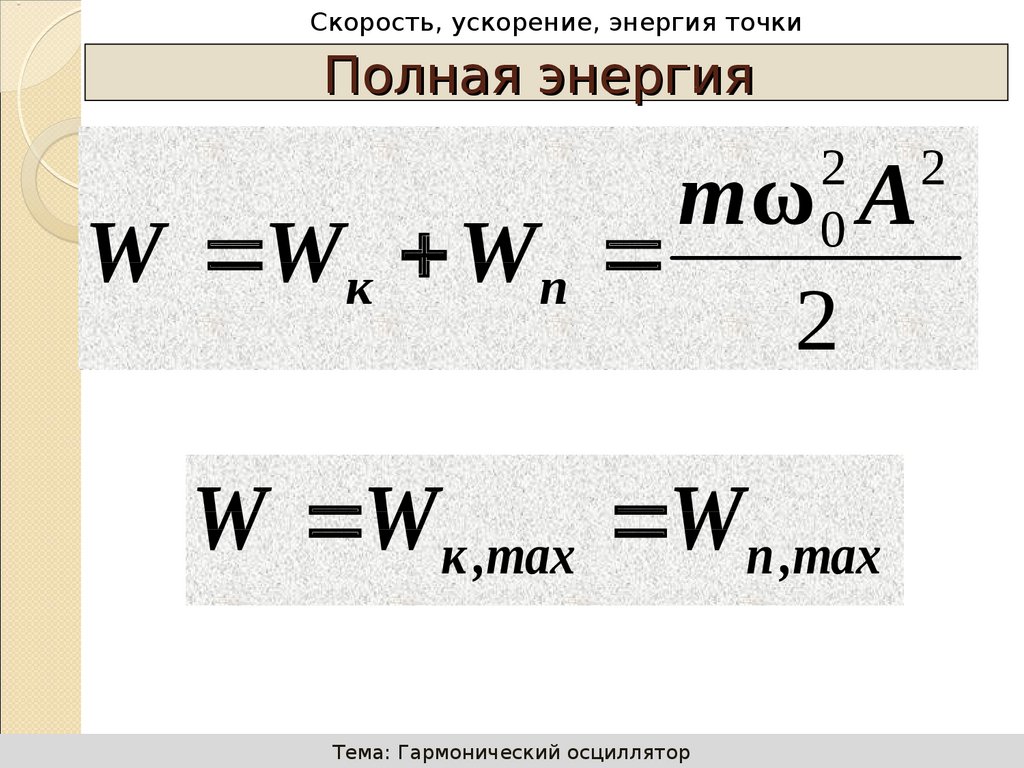



















 Физика
Физика








