Похожие презентации:
Колебания и волны. Лекция 14
1. Колебания и волны
2.
Колебаниями называются движения или процессы,которые обладают определенной повторяемостью
во времени.
3.
Колебания сопровождаютсяпопеременным превращением
энергии одного вида в энергию
другого вида.
4.
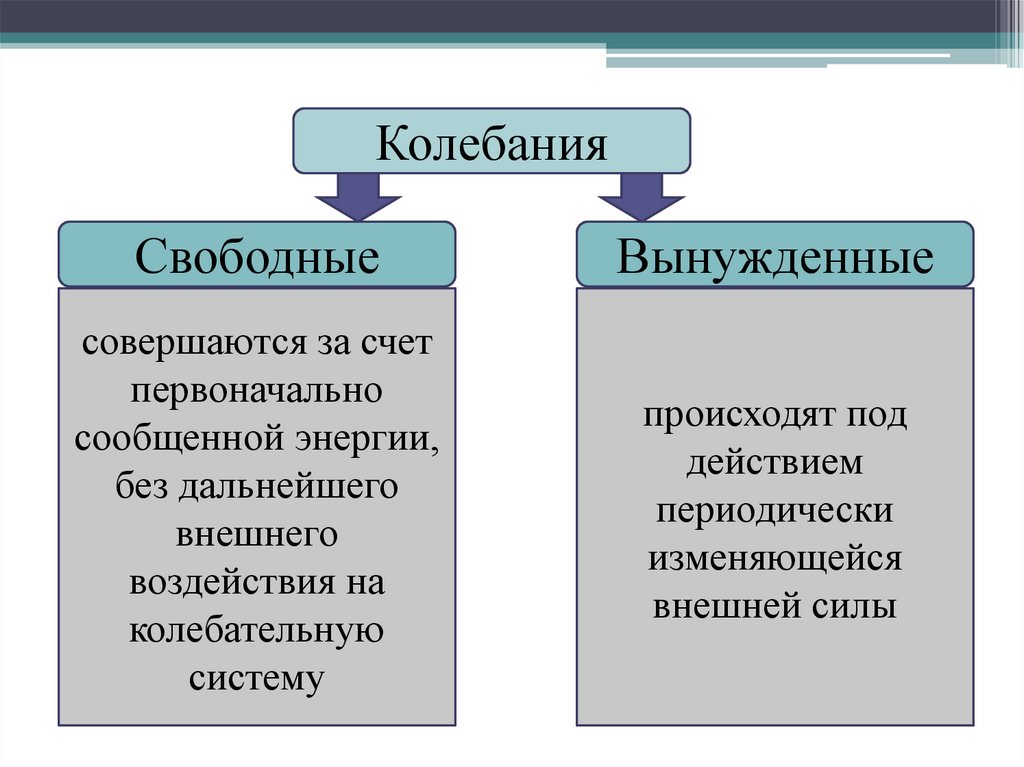
КолебанияСвободные
Вынужденные
совершаются за счет
первоначально
сообщенной энергии,
без дальнейшего
внешнего
воздействия на
колебательную
систему
происходят под
действием
периодически
изменяющейся
внешней силы
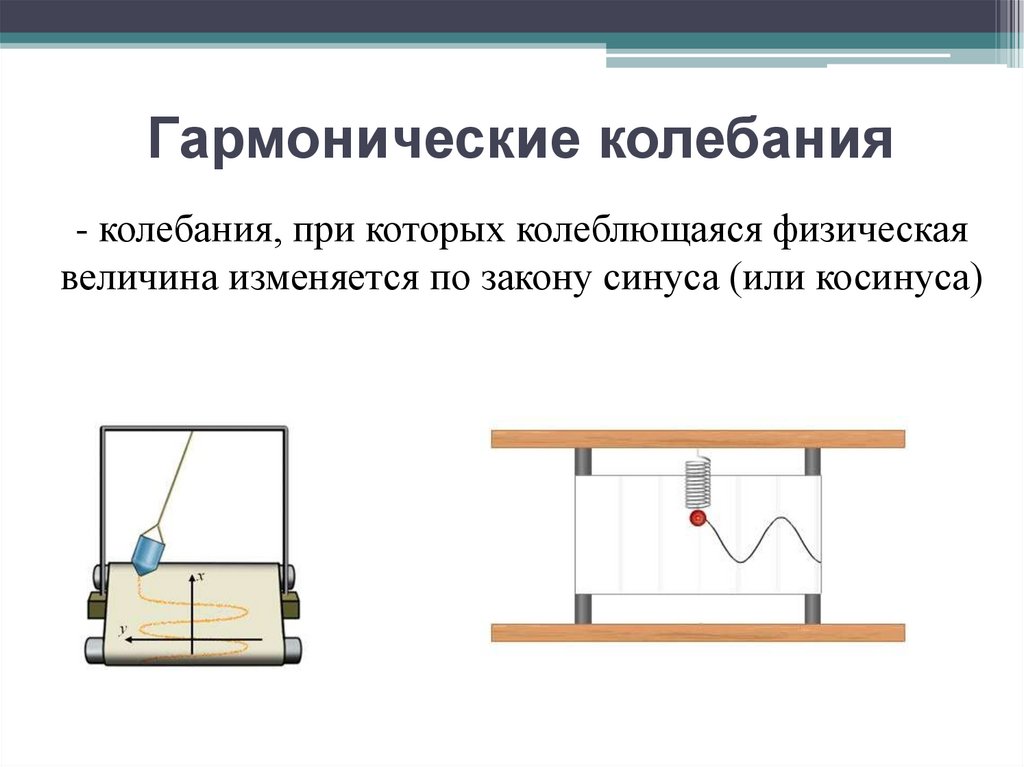
5. Гармонические колебания
- колебания, при которых колеблющаяся физическаявеличина изменяется по закону синуса (или косинуса)
6. Уравнение гармонических колебаний
s A cos( t 0 )• А – амплитуда колебания – максимальное
значение колеблющейся величины;
• – круговая (циклическая) частота;
• 0 – начальная фаза колебания;
• t 0 – фаза колебания в данный момент времени
7. Период колебаний
T – наименьший промежуток времени, по истечениикоторого повторяются состояния колеблющейся
системы (совершается одно полное колебание)
t
T
N
[T ] 1 c
(t T ) ( t ) 2
T
2
8. Частота колебаний
v – величина обратная периоду колебаний – числополных колебаний, совершаемых в единицу времени
N
t
[ ] 1 c 1 Гц
1
1 Герц – частота периодического процесса, при котором
за 1 с совершается один цикл колебаний
1
T
2
9. Дифференциальное уравнение гармонических колебаний
s A cos( t 0 )ds
s
A sin( t 0 ) A cos( t 0 )
dt
2
2
d s
s 2 A 2 cos( t 0 ) A 2 cos( t 0 )
dt
d 2s
2
s 0
2
dt
s 2 s 0
10. Решение дифференциального уравнения гармонических колебаний
d 2s2
s 0
2
dt
s A cos( t 0 )
11. Метод векторных диаграмм
s A cos( t 0 )12. Механические гармонические колебания
x A cos( t 0 )v x A cos( t 0
2
)
a x A 2 cos( t 0 )
13. Механические гармонические колебания
x A cos( t 0 )F ma mA 2 cos( t ) m 2 x
m 2 x 2 mA2 2
U Fdx
cos 2 ( t 0 )
2
2
0
x
mv 2 mA2 2
E
sin 2 ( t 0 )
2
2
mA2 2
1 cos 2( t 0 )
2
mA2 2 mA2 2
cos 2( t 0 )
2
2
14. Полная энергия
mA2 2Eполн E U
2
Полная энергия остается постоянной, с течением
времени происходит только превращение
кинетической энергии в потенциальную и обратно.
15. Гармонический осциллятор
система, совершающая колебания, описываемыедифференциальным уравнением
s 2 s 0
Примерами гармонического осциллятора являются
пружинный, математический и физический
маятники, электрический колебательный контур.
16. Пружинный маятник
- это груз массой m,подвешенный на абсолютно
упругой пружине и
совершающий
гармонические колебания
под действием упругой силы
F kx
где k – жесткость пружины
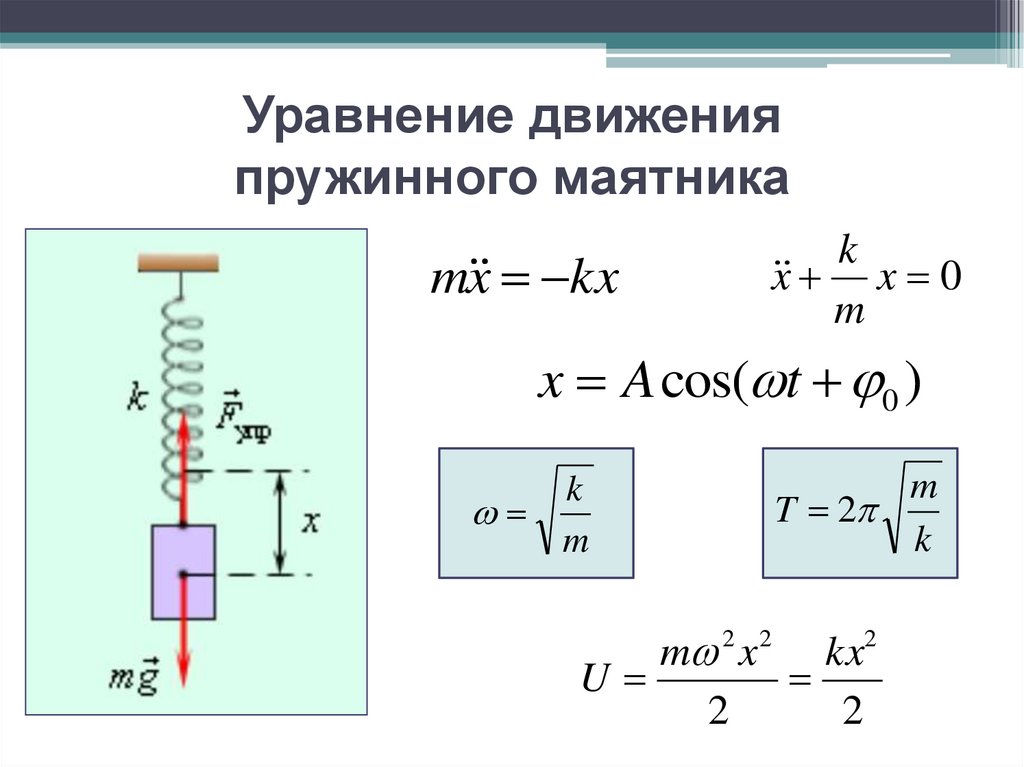
17. Уравнение движения пружинного маятника
m x kxk
x x 0
m
x A cos( t 0 )
k
m
m
T 2
k
m 2 x 2 kx2
U
2
2
18. Математический маятник
– идеализированная система,состоящая из материальной
точки массой m, подвешенной
на невесомой нерастяжимой
нити длиной l , и колеблющейся
под действием силы тяжести
без трения.
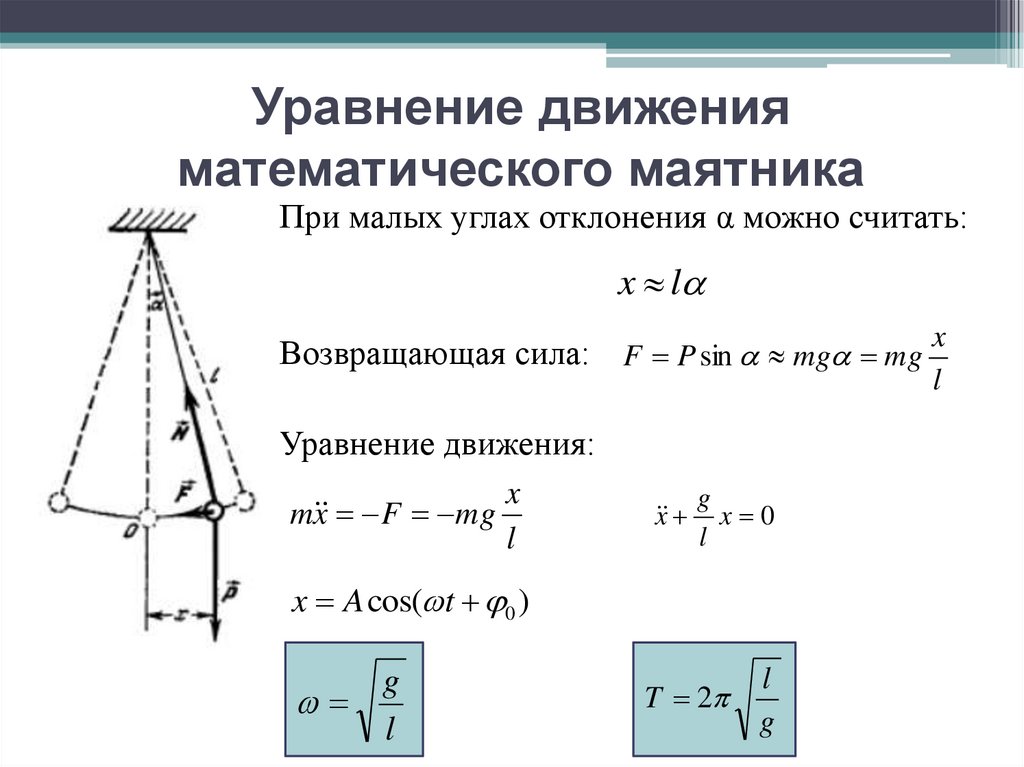
19. Уравнение движения математического маятника
При малых углах отклонения α можно считать:x l
Возвращающая сила: F P sin mg mg
Уравнение движения:
m x F mg
x
l
x
g
x 0
l
x A cos( t 0 )
g
l
l
T 2
g
x
l
20. Физический маятник
– твердое тело,совершающее под
действием силы тяжести
колебания вокруг
горизонтальной оси
подвеса, не проходящей
через центр масс тела.
21. Уравнение движения физического маятника
J mgd 0mgd
0
J
0 cos( t 0 )
mgd
J
J
T 2
mgd
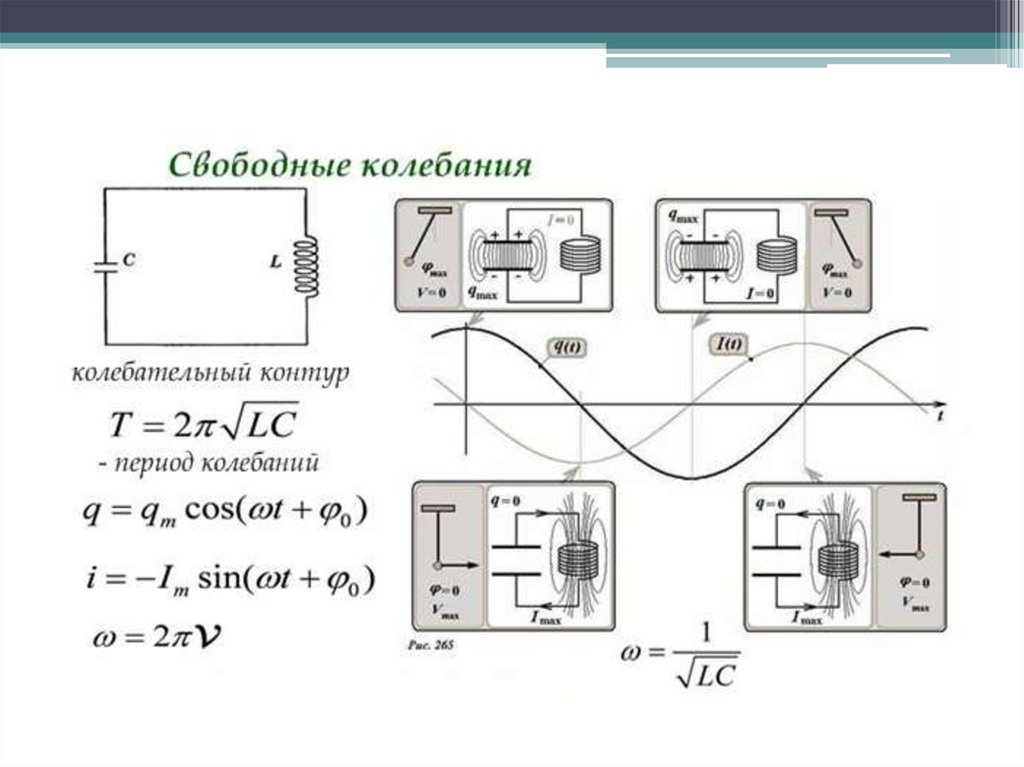
22. Электрический колебательный контур
- электрическая цепь, состоящаяиз включенных
последовательно катушки
индуктивностью L,
конденсатора емкостью С и
резистора сопротивлением R.
23. Дифференциальное уравнение свободных гармонических колебаний в колебательном контуре
d 2q 1q 0
dt LC
q qmax cos( t 0 )
1
LC
T 2 LC
24.
25. Затухающие колебания
- колебания, амплитуды которых из-за потерьэнергии реальной колебательной системой с
течением времени уменьшаются.
Идеализированные реальные системы, в которых
параметры определяющие физические свойства
системы, в ходе процесса не изменяются
называются линейными.
26. Дифференциальное уравнение свободных затухающих колебаний линейной системы
d 2sds
2
2
s 0
2
dt
dt
s – колеблющаяся величина,
δ= const – коэффициент затухания
ω – циклическая частота свободных незатухающих
колебаний той же колебательной системы (при δ=0)
27. Затухающие колебания
28. Период затухающих колебаний
- промежуток времени между двумя последующимимаксимумами колеблющейся физической
величины
T
2
2
2 2
29. Декремент затухания
A(t )e T
A(t T )
A(t) и A(t+T) – амплитуды двух последовательных колебаний,
соответствующих моментам времени, отличающихся на период
Логарифмический декремент затухания
A(t )
T 1
Θ ln
T
A(t T )
N
N – число колебаний, совершаемых за время уменьшения
амплитуды в e раз
30. Добротность колебательной системы
- безразмерная величина Q, равная произведению 2π наотношение энергии W(t) колебаний системы в произвольный
момент времени t к убыли этой энергии за промежуток
времени t к убыли этой энергии за промежуток времени от t до
t+T (за один условный период затухающих колебаний)
W (t )
Q 2
W (t ) W (t T )
31. Резонанс
- явление резкого возрастания амплитуды вынужденныхколебаний при приближении частоты вынуждающей силы
(или, в случае электрических колебаний, частоты
вынуждающего переменного напряжения) к частоте равной
или близкой собственной частоте колебательной системы.
рез 2 2 2
Aрез
Xm
2 2 2
32. Волны
Волновой процесс или волна – процесс распространенияколебаний в сплошной среде.
Основное свойство волн – перенос энергии без переноса
вещества (независимо от природы волн).
Сплошная среда – непрерывно распределенная в
пространстве и обладающая упругими свойствами.
Упругие (механические) волны – механические возмущения,
распространяющиеся в упругой среде
33.
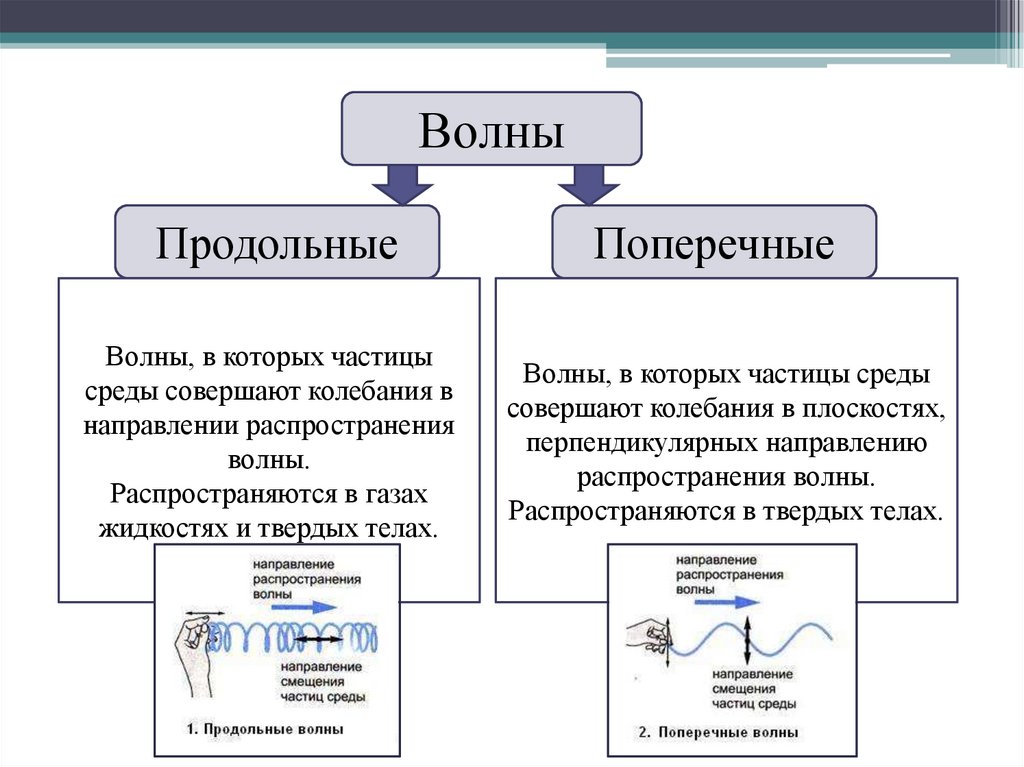
ВолныПродольные
Поперечные
Волны, в которых частицы
среды совершают колебания в
направлении распространения
волны.
Распространяются в газах
жидкостях и твердых телах.
Волны, в которых частицы среды
совершают колебания в плоскостях,
перпендикулярных направлению
распространения волны.
Распространяются в твердых телах.
34.
Волновая поверхность(фронт) – геометрическое
место точек до которых
доходят колебания к
моменту времени t.
Скорость распространения волны (фазовая скорость) –
физическая величина, определяемая расстоянием, проходимым
за единицу времени любой точкой волновой поверхности.
35. График гармонической поперечной волны, распространяющейся со скоростью v вдоль оси Х
График волныпредставляет зависимость
смещения всех частиц
среды от расстояния до
источника колебаний в
данный момент времени
( x, t )
36. Уравнение плоской волны
x( x, t ) A cos t 0
v
A = const – амплитуда волны
ω – циклическая частота
φ0 – начальная фаза
v – скорость распространения волны (фазовая скорость)
x – расстояние от источника колебаний до какой-либо точки
волны
x
t 0 – фаза плоской волны
v
37. Волновое число
22
k
vT v
Уравнение бегущей гармонической волны
( x, t ) A cos( t kx 0 )
38. Уравнение сферической волны
A(r , t ) cos( t kr 0 )
r
r – расстояние от центра волны до рассматриваемой точки
среды.
39. Волновое уравнение
2 2 2 1 22 2 2 2
2
x
y
z
v t
1 2
2 2
v t
Δ – оператор Лапласа
Решением волнового уравнения является уравнение
любой волны (в том числе плоская и сферическая)
40. Принцип суперпозиции
При распространении в линейной среде нескольких волнкаждая из них распространяется так, как будто другие волны
отсутствуют, а результирующее смещение частицы среды в
любой момент времени равно геометрической сумме
смещений, которые получают частицы, участвующие в каждом
из слагающих волновых процессов.
41. Когерентные волны
Когерентностью называется согласованноепротекание во времени и пространстве
нескольких колебательных или волновых
процессов.
Две волны называются когерентными, если их
разность фаз не зависит от времени.
42. Интерференция волн
Интерференцией волн называется явление наложенияволн, при котором происходит устойчивое во времени
их взаимное усиление в одних точках пространства и
ослабление в других в зависимости от соотношения
между фазами этих волн.
43.
44. Интерференционный максимум и минимум
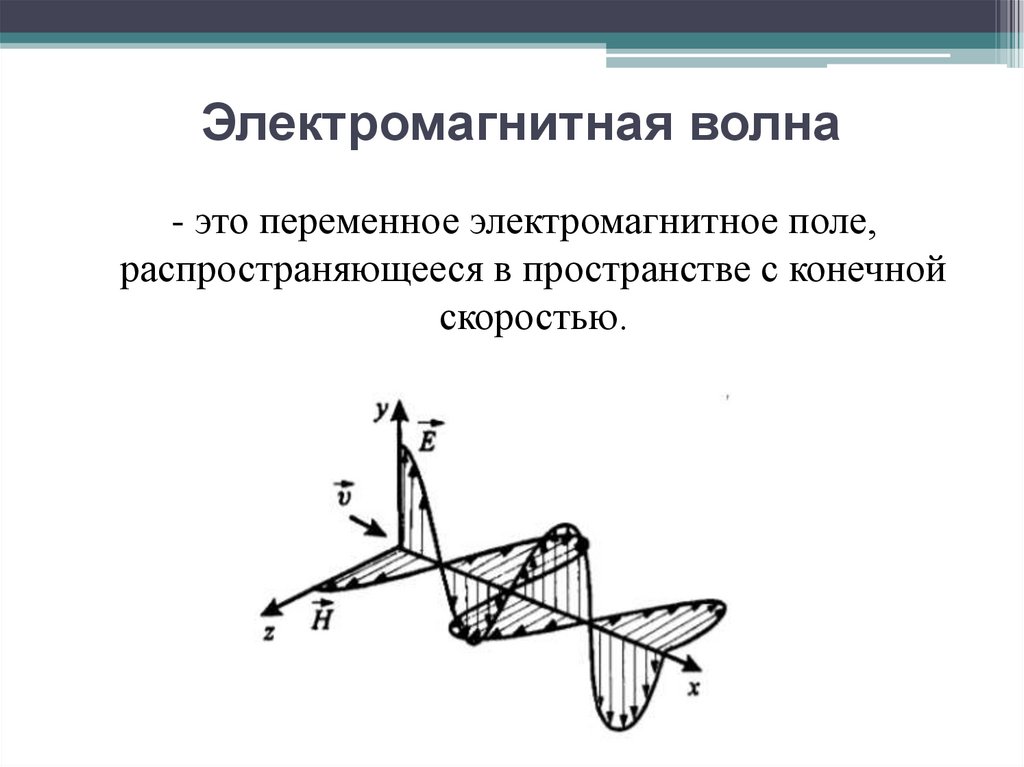
45. Электромагнитная волна
- это переменное электромагнитное поле,распространяющееся в пространстве с конечной
скоростью.
46. Свойства электромагнитных волн
• электромагнитная волна – поперечная• электромагнитные волны распространяются в
вакууме с конечной скоростью 3·108 м/с
• в электромагнитной волне векторы Е и Н
пропорциональны друг другу
0 E 0 H
47. Электромагнитная волна
2Eyx 2
2
1 Ey
2 2
v t
E y E0 cos( t kx )
2H z
1 2H z
2 2
2
x
v
t
H z H 0 cos( t kx )
E0 и H0 – амплитуды напряженностей электрического и
магнитного полей волны,
ω – циклическая частота волны,
k = ω/v – волновое число,
φ – начальная фаза колебаний.
48. Энергия электромагнитной волны
Объемная плотность энергии электромагнитной волныскладывается из объемных плотностей энергий электрического
и магнитного полей
0 E 2 0 H 2
w we wm
2
2
0 E 0 H
Плотность потока энергии
w 0 0 EH
S wv EH
49. Вектор Умова-Пойтинга
– вектор плотности потока энергии электромагнитной волныS [E, H ]
Вектор S плотности потока энергии электромагнитной
волны направлен в сторону распространения эмв, а его модуль
равен энергии, переносимой эмв за единицу времени через
единичную площадку, перпендикулярную направлению
распространения волны.
Скалярная величина I, модулю среднего значения вектора
Умова – Пойтинга, называется интенсивностью волны
I S










































 Физика
Физика








