Диэлектрики в электрическом поле. Лекция №4

1.

Лекция № 4
ДИЭЛЕКТРИКИ В
ЭЛЕКТРИЧЕСКОМ ПОЛЕ
56
1

2.

ВОПРОСЫ
12. Диэлектрики в электрическом
поле. Полярные и неполярные
диэлектрики. Поляризация
диэлектриков. Поляризованность.
Вектора E, D, P. Заряды связанные и
сторонние. Теорема Остроградского
Гаусса.
56
2

3.

13. Граничные условия. Граничные
условия на границе двух
диэлектриков. Граничные условия на
границе проводник-диэлектрик.
56
3

4.

12. Диэлектрики в электрическом
поле.
Полярные и неполярные
диэлектрики.
Поляризация диэлектриков.
Поляризованность.
Вектора E, D, P.
Заряды связанные и сторонние.
Теорема Остроградского-Гаусса.
56
4

5.

Известно, что все вещества в
электрическом отношении при
нормальных условиях делятся на
проводники, полупроводники и
диэлектрики.
Вещества, при нормальных
условиях, не проводящие
электрический ток, называют
диэлектриками (изоляторами).
56
5

6.

При внесении диэлектрика во
внешнее электрическое поле
происходит поляризация, т.е.
смещение зарядов, входящих в
состав молекул, в соответствии с их
знаком.
В результате на поверхности
диэлектрика возникают связанные
заряды, неспособные свободно
перемещаться по диэлектрику.
56
6

7.

Молекулы диэлектриков
электрически нейтральны.
Суммарный заряд электронов и
ядер, входящих в состав молекулы
равен нулю.
Их в первом приближении можно
рассматривать как электрический
диполь с дипольным моментом
p = qℓ,
56
7

8.

где q – суммарный положительный
заряд всех атомных ядер, равный по
абсолютной величине суммарному
заряду всех электронов в молекуле;
ℓ – вектор, проведенный из «центра
тяжести» отрицательного заряда,
созданного всеми электронами в
молекуле, в «центр тяжести»
положительного заряда атомных
ядер.
56
8

9.

В зависимости от внутреннего
строения диэлектрики относят к
неполярным, полярным, ионным,
сегнетоэлектрикам и др.
К неполярным диэлектрикам
относятся, например, молекулы
водорода Н2, азота N2, кислорода О2
и др.
56
9

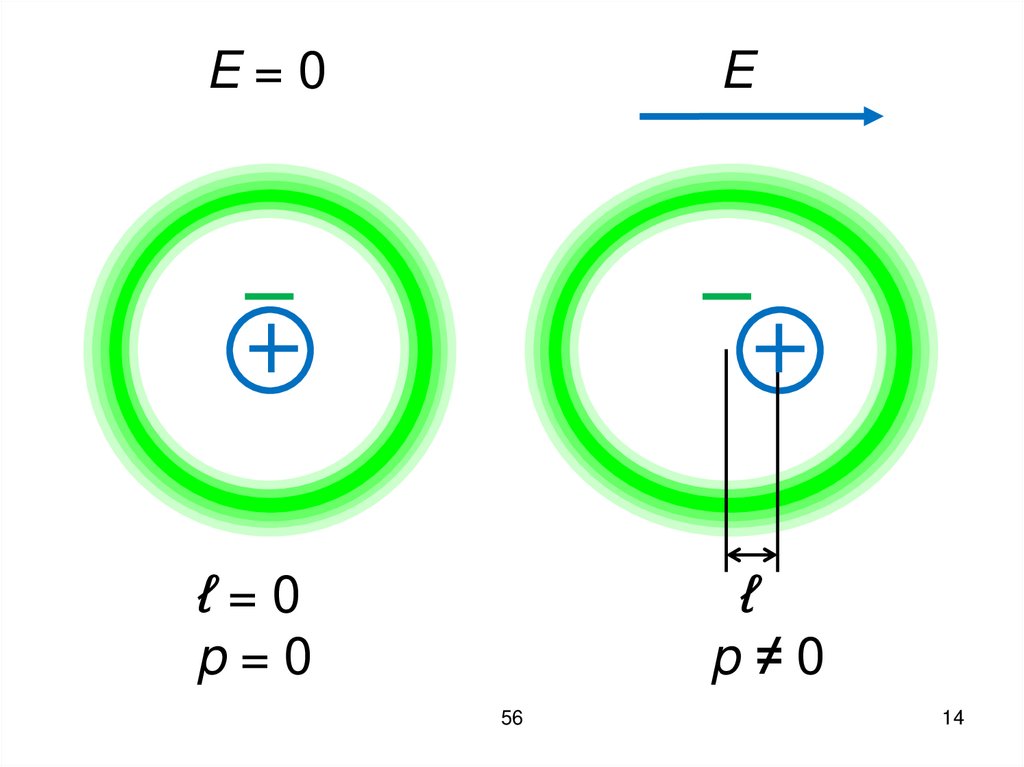
10.

В таких диэлектриках в отсутствии
внешнего электрического поля
(Е = 0) “центры тяжести”
положительных и отрицательных
зарядов совпадают (ℓ = 0) и
дипольный момент каждой молекулы
равен нулю.
Суммарный дипольный момент
диэлектрика в целом также равен
нулю.
56
10

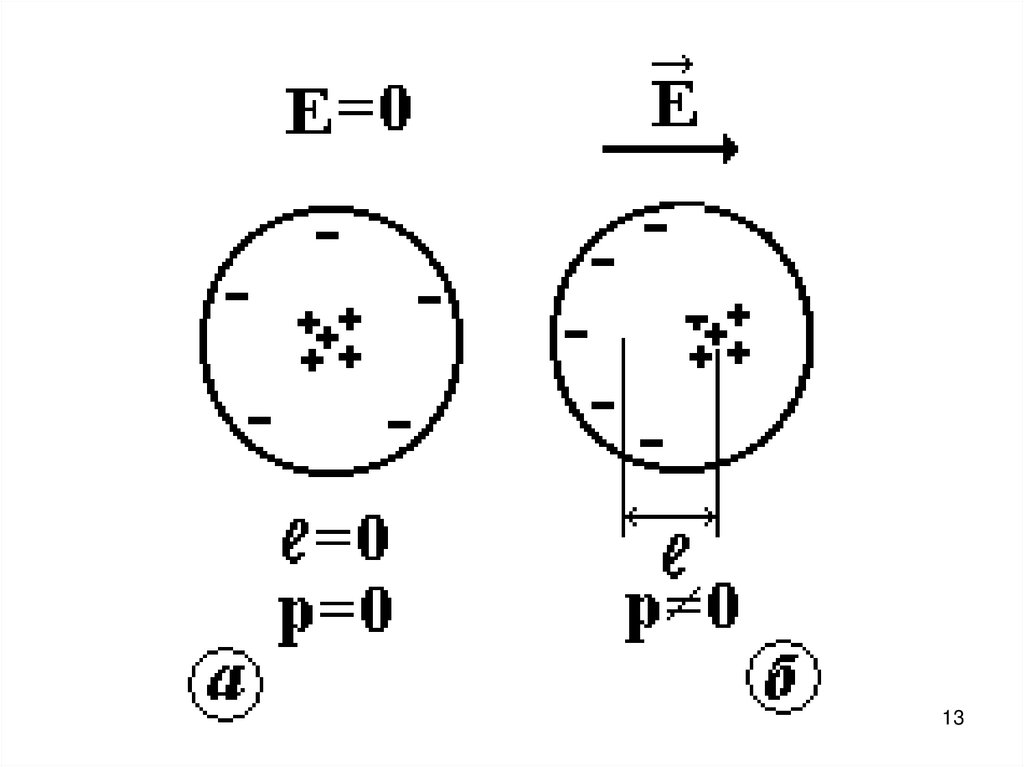
11.

При внесении неполярного
диэлектрика во внешнее
электрическое поле (Е 0)
происходит деформация
электронных оболочек атомов и
молекул.
«Центры тяжести» положительных и
отрицательных зарядов смещаются
друг относительно друга (ℓ 0).
56
11

12.

Поэтому молекулы неполярного
диэлектрика приобретают
наведенный дипольный момент
p E.
Такая поляризация называется
электронной.
56
12

13.

56
13

14.

E=0
E
ℓ=0
p=0
ℓ
p≠0
56
14

15.

К полярным диэлектрикам относятся
вода (Н2О), спирты и др.
Молекулы полярных диэлектриков
из-за особенностей своего строения
уже в отсутствии внешнего
электрического поля (Е = 0) имеют
дипольный момент, не равный нулю
(p 0). Из-за теплового хаотического
движения молекул суммарный
дипольный момент диэлектрика в
целом равен нулю.
56
15

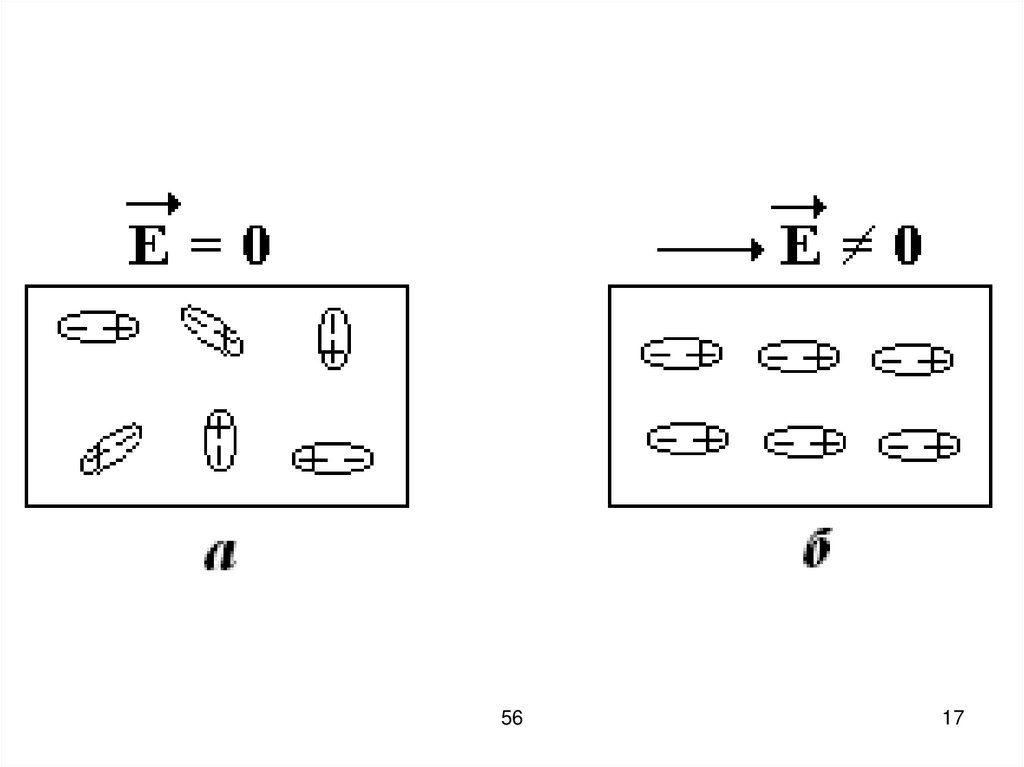
16.

При внесении полярного
диэлектрика во внешнее
электрическое поле молекулы
переориентируются, их дипольные
моменты выстраиваются по полю.
В итоге, суммарный дипольный
момент всех молекул полярного
диэлектрика уже не равен нулю.
Такая поляризация называется
дипольной или ориентационной.
56
16

17.

56
17

18.

Есть также ионная поляризация в
ионных кристаллах.
Ионная поляризация – смещение
ионов, положительных по полю,
отрицательных – против поля.
В результате появляется не
скомпенсированное распределение
зарядов в диэлектрике –
поляризация.
56
18

19.

Если диэлектрик однородный, то
нескомпенсированный заряд
появляется только на поверхности.
Для количественного описания
поляризации диэлектрика вводят
вектор поляризации P
(поляризованность).
56
19

20.

Поляризованностью называют
геометрическую сумму дипольных
моментов молекул единицы объема
диэлектрика.
n
1
P
pi
V i 1
В Си единицей измерения
поляризованности является Кл/м2.
56
20

21.

При внесении диэлектриков в
электрическое поле на их
поверхности и в объеме появляются
нескомпенсированные заряды
(заряды, связанные с молекулами
диэлектрика).
Такие нескомпенсированные заряды,
появившиеся в результате
поляризации диэлектрика, называют
связанными зарядами (q*, ρ* –
плотность связанных зарядов).
56
21

22.

Связанные заряды описывают
вектором поляризованности P.
Заряды, входящие в состав молекул
диэлектрика, называются
связанными.
56
22

23.

Заряды, которые не входят в состав
молекул диэлектрика, называют
сторонними.
Эти заряды могут находиться как
вне, так и внутри диэлектрика.
Для описания сторонних зарядов
(q, ρ) используют вектор
электростатической индукции D
(вектор электрического смещения),
который измеряется в Кл/м2.
56
23

24.

Теорема Гаусса для вектора
поляризации P
(и для связанных зарядов q*, ρ*)
в интегральной и
в дифференциальной форме.
Вектор P вне диэлектрика не
существует.
(
P
d
S
n
)
q
*
( P) ρ
56
24
*

25.

Теорема Гаусса для вектора
индукции D
(и для сторонних зарядов q, ρ)
в интегральной и
в дифференциальной форме.
(
D
d
S
n
)
q
( D) ρ
56
25

26.

Теорема Гаусса для вектора
напряжённости Е
в интегральной и
в дифференциальной форме.
ε
(
E
d
S
n
)
q
q
*
0
ε 0 ( E ) ρ ρ *
56
26

27.

Электрические свойства диэлектрика
описывают с помощью двух величин.
ε – диэлектрическая проницаемость,
которая равна отношению
напряжённости электрического поля
в вакууме Е0 к напряжённости
электрического поля в диэлектрике
Е.
E0
ε
E
56
27

28.

χ – диэлектрическая
восприимчивость, пропорциональна
отношению поляризации P к
напряжённости поля в вакууме E0
P ε
χ
ε -1
E0 ε 0
56
28

29.

Связь между векторами E, D, P
D ε o E P
ε
D P
χ
P ε o χ E
D ε oε E
56
29

30.

56
30

31.

13. Граничные условия.
Граничные условия на границе двух
диэлектриков.
Граничные условия на границе
проводник-диэлектрик.
56
31

32.

Введём единичный вектор n,
перпендикулярный плоскости
соприкосновения двух тел, и
единичный вектор τ, лежащий в
плоскости соприкосновения двух тел,
т.е. по касательной.
n
τ
56
32

33.

Рассмотрим два диэлектрика.
Одному диэлектрику присвоим
номер 1, другому – номер 2.
Все вектора, которые находятся
в 1-м диэлектрике будут иметь
индекс «1». Вектора во втором
диэлектрике будут иметь индекс «2».
У первого диэлектрика
диэлектрическая проницаемость ε1,
у второго – ε2.
56
33

34.

Найдем связь между
поляризованностью Р и
поверхностной плотностью *
связанных зарядов на границе
раздела двух изотропных
диэлектриков.
У таких диэлектриков нет объемного
избыточного связанного заряда, а
имеется только поверхностный
связанный заряд.
56
34

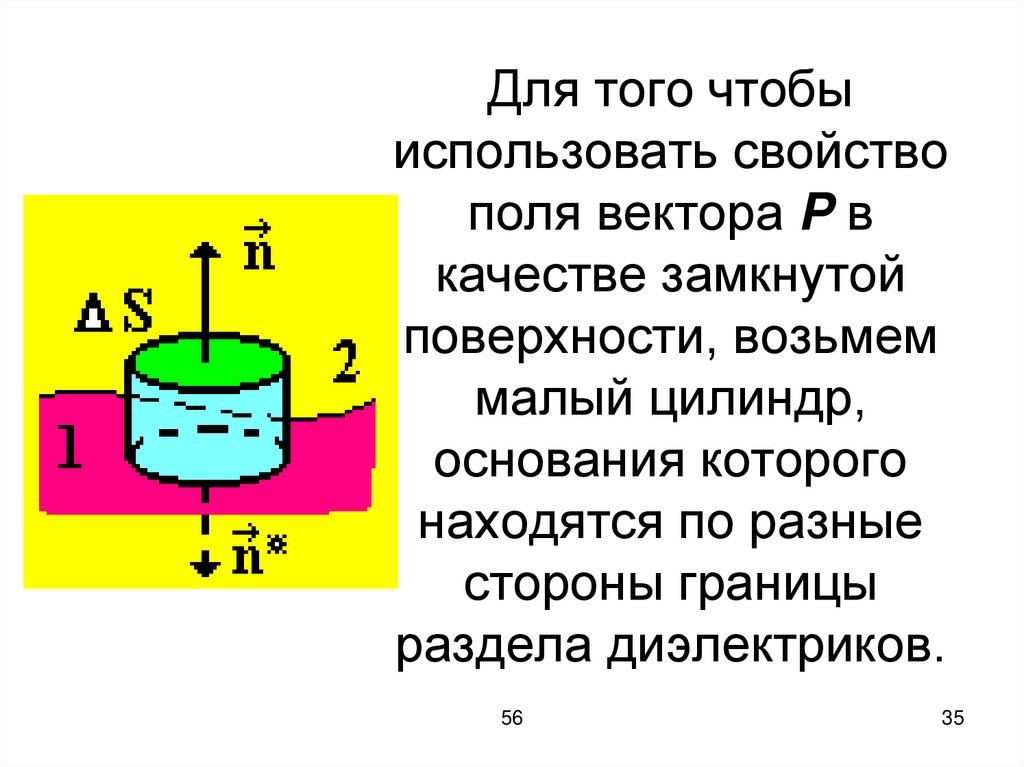
35.

Для того чтобы
использовать свойство
поля вектора P в
качестве замкнутой
поверхности, возьмем
малый цилиндр,
основания которого
находятся по разные
стороны границы
раздела диэлектриков.
56
35

36.

Найдем поток вектора P сквозь
цилиндрическую поверхность с
учетом того, что этот поток через
боковую поверхность цилиндра
равен нулю.
В этом случае будем учитывать
только поток сквозь основания
цилиндра, т. е.
(P*1n+ Р2n) S = * S,
56
36

37.

где P*1n и Р2n проекции вектора P в
диэлектрике 1 на нормаль n* и в
диэлектрике 2 на нормаль n.
Вследствие того, что P*1n = P1n,
предыдущее равенство перепишем
после сокращения на S в виде
Р2n P1n = *.
Вывод: На границе раздела двух
изотропных диэлектриков
нормальная составляющая вектора
P испытывает разрыв.
56
37

38.

Если второй средой является
вакуум, то Р2n= 0, тогда формула
принимает более простой вид:
Рn = *,
где Рn проекция вектора P на
нормаль к поверхности диэлектрика.
Знак проекции Рn определяет знак
поверхностного
связанного заряда *.
56
38

39.

Получим выражения для векторов
напряжённости Е и индукции D на
границе двух диэлектриков.
Пусть на границе раздела двух
диэлектриков находится сторонний
поверхностный заряд.
Для нахождения условия будем
использовать теорему о циркуляции
вектора Е и теорему Гаусса для
вектора D.
56
39

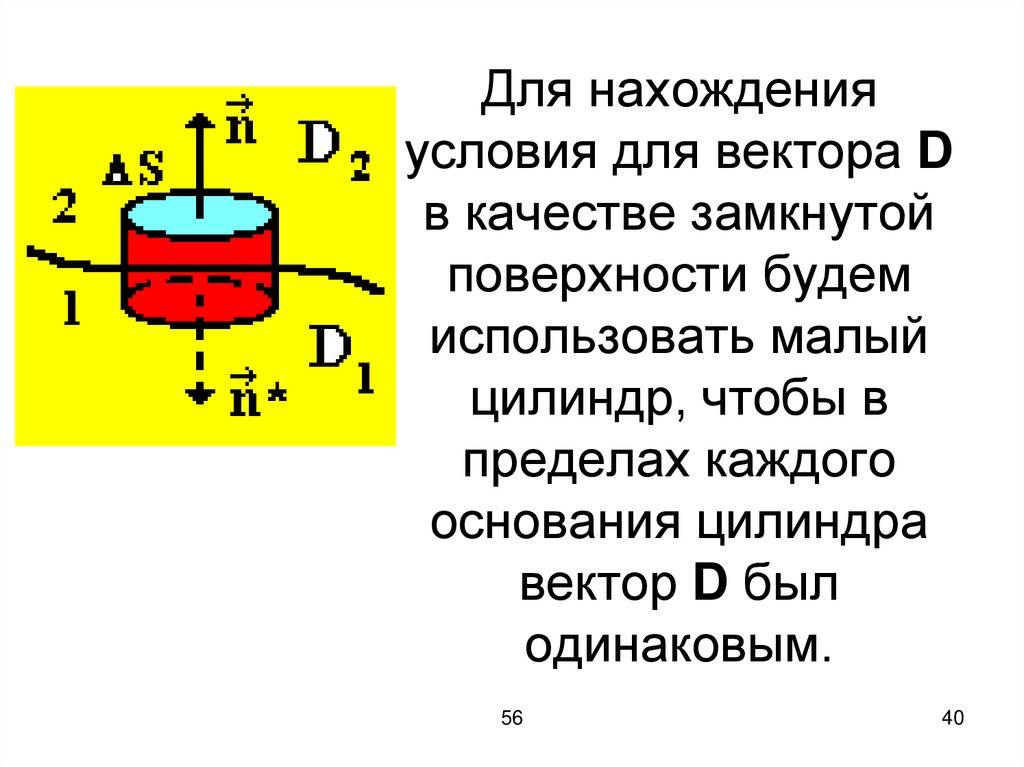
40.

Для нахождения
условия для вектора D
в качестве замкнутой
поверхности будем
использовать малый
цилиндр, чтобы в
пределах каждого
основания цилиндра
вектор D был
одинаковым.
56
40

41.

Используя теорему Гаусса для
вектора D, получаем
(D1n* + D2n) S = S,
где поверхностная плотность
стороннего заряда на границе
раздела.
С учетом того, что
D1n* = D1n
последнее равенство принимает вид:
D2n D1n = .
56
41

42.

Вывод: нормальная составляющая
вектора испытывает скачок на
границе раздела двух диэлектриков.
Если сторонние заряды отсутствуют
(σ = 0) на границе раздела, то
D2n = D1n
т. е. нормальная составляющая
вектора D скачка не испытывает.
56
42

43.

Воспользуемся формулой D = ε0εЕ и
для случая D2n = D1n получим
следующее выражение
ε 2 Е 2n = ε 1 Е 1n.
Отсюда
E1n ε 2
E2 n ε 1
Вектор Еn на границе испытывает
разрыв.
56
43

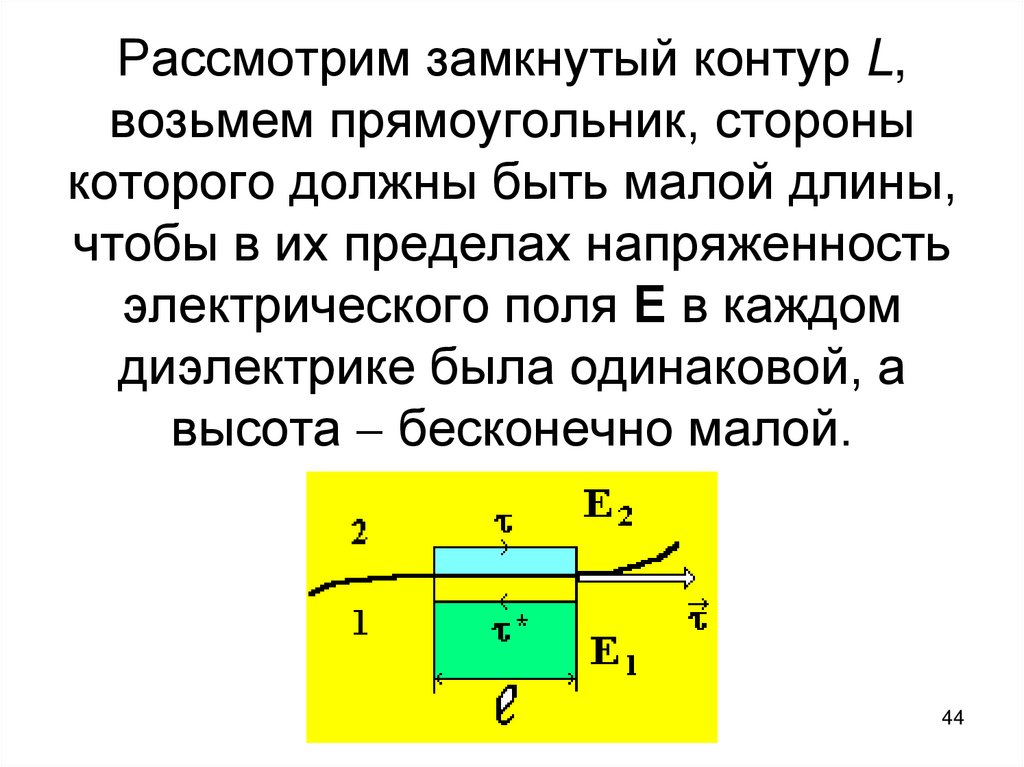
44.

Рассмотрим замкнутый контур L,
возьмем прямоугольник, стороны
которого должны быть малой длины,
чтобы в их пределах напряженность
электрического поля Е в каждом
диэлектрике была одинаковой, а
высота бесконечно малой.
56
44

45.

На основании теоремы о циркуляции
вектора Е имеем
(Е1 *+ Е2 ) = 0,
где Е1 * и Е2 проекции вектора Е
на единичный вектор касательной τ,
взяты в направлении обхода
контура.
Если использовать в качестве
общего единичный вектор τ, то
Е1 * = Е1 .
56
45

46.

Тогда предыдущее равенство
принимает вид
Е1 = Е2 .
Вывод: Тангенциальная
составляющая вектора Е одинакова
по разные стороны границы раздела,
т. е. не испытывает скачка.
56
46

47.

Воспользуемся формулой D /ε0ε = Е.
D1τ D2 τ
ε 0ε1 ε 0ε 2
Отсюда
D1τ ε1
D2 τ ε 2
Вектор D испытывает разрыв.
56
47

48.

Преломление линий E, D.
При переходе из одной
диэлектрической среды с
диэлектрической проницаемостью ε1
в диэлектрическую среду с
диэлектрической проницаемостью ε2
вектор электрической напряжённости
Е и вектор электрической индукции D
испытывают следующие изменения
на границе раздела двух сред.
56
48

49.

Тангенциальная составляющая
вектора напряжённости одинакова
по разные стороны границы раздела,
т. е. не испытывает скачка:
Е1 = Е2
Нормальная составляющая вектора
напряжённости различна по разные
стороны границы раздела, т. е.
испытывает скачок:
E1n ε 2
E2 n ε1
56
49

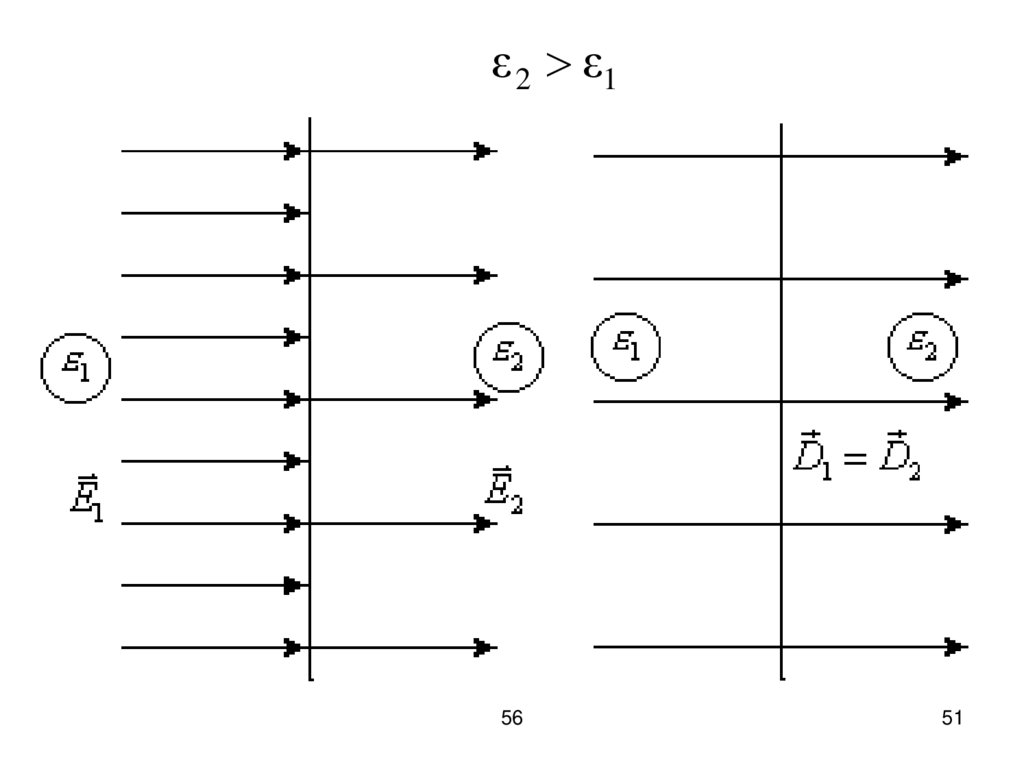
50.

Нормальная составляющая вектора
индукции одинакова по разные
стороны границы раздела, т. е. не
испытывает скачка:
D1n = D2n
Тангенциальная составляющая
вектора индукции различна по
разные стороны границы раздела,
т.е. испытывает скачок:
D1 ε1
D2 ε 2
56
50

51.

ε 2 ε1
56
51

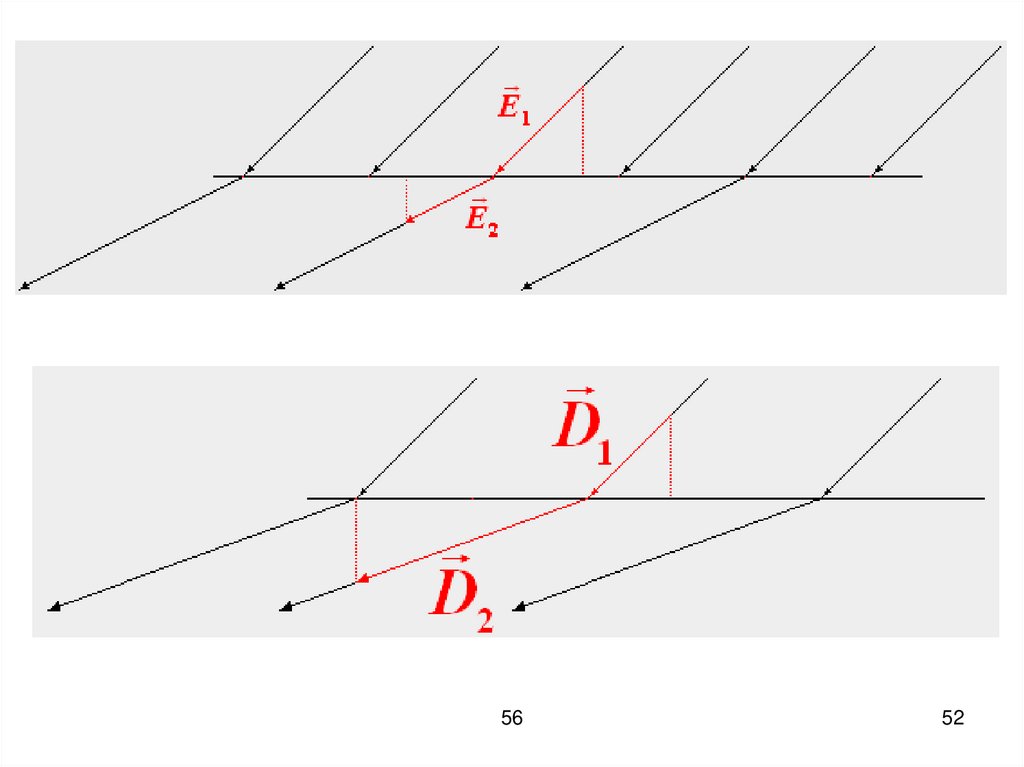
52.

56
52

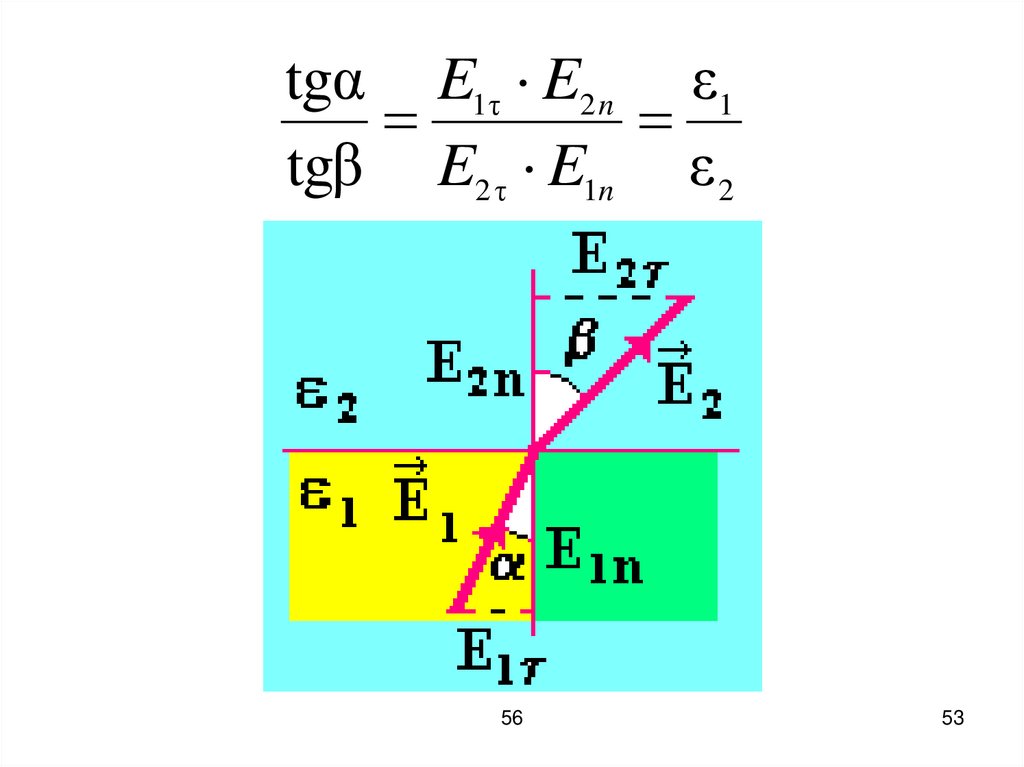
53.

tgα E1τ E2 n ε1
tgβ E2 τ E1n ε 2
56
53

54.

Граничные условия на поверхности
проводник-диэлектрик
На границе раздела:
проводник диэлектрик
(среда 1 проводник,
среда 2 диэлектрик) имеем
Dn = ,
где n внешняя нормаль к
поверхности проводника.
56
54

55.

Вывод: В состоянии равновесия
электрическое поле внутри
проводника отсутствует,
следовательно, и его
поляризованность равна нулю.
Поэтому электрическая индукция
равна нулю (D = 0) внутри
проводника.
56
55

56.

Замечание: Если к поверхности
заряженного проводника прилегает
однородный изотропный диэлектрик,
то на их границе появляются
связанные заряды плотности *
(объемная плотность связанных
зарядов * = 0).
56
56

57.

Но на границе проводник диэлектрик
есть сторонние и связанные заряды.
Поэтому, применяя теорему Гаусса
к вектору Е, получаем
σ σ
En
ε0
или
*
Dn
σ
En
εε 0 εε 0
56
57

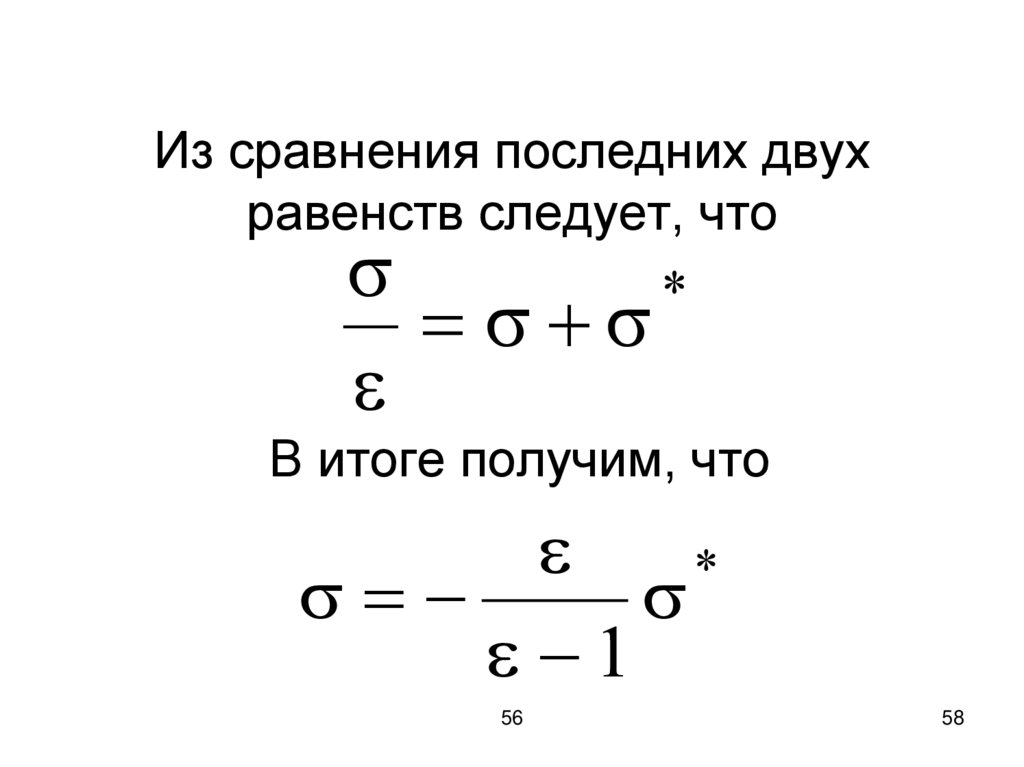
58.

Из сравнения последних двух
равенств следует, что
*
В итоге получим, что
*
1
56
58

59.

Вывод: Поверхностная плотность
сторонних зарядов на проводнике
однозначно связана с поверхностной
плотностью связанного заряда * в
диэлектрике, но знаки этих зарядов
противоположны.
56
59

60.

56
60