Похожие презентации:
Прикладні задачі. Розв’язування прямокутних трикутників
1.
Тема урокуПрикладні задачі.
Розв’язування прямокутних
трикутників.
2.
• Мета уроку:• закріпити знання тригонометричних функцій
гострого кута прямокутного трикутника,
• -навчитися знаходити невідомі елементи
прямокутного трикутника по відомих двом
його елементам,
• -застосовувати теоретичні знання для
вирішення практичних завдань,
• -удосконалювати уміння застосовувати
теорему Піфагора при рішенні прикладних
завдань;
• - показати учням на прикладах її практичне
вживання в повсякденному житті
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
Вірю чи не вірю1.У прямокутному
трикутнику квадрат
гіпотенузи дорівнює сумі
квадратів катетів.
14.
Вірю чи не вірю2.Сума гострих кутів
прямокутного
трикутника дорівнює
180 градусів
15.
Вірю чи не вірю3.Основна
тригонометрична
тотожність має
вигляд:
sin2α + cos2α = 1
16.
Вірю чи не вірю4. Трикутник, у якого є
прямий кут , називається
гострокутним
17.
Вірю чи не вірю5.Сторона прямокутного
трикутника, що лежить проти
прямого кута, називається
гіпотенуза
18.
Вірю чи не вірю6.Висота, проведена
до гіпотенузи, ділить
трикутник на три
подібних
трикутника
19.
Вірю чи не вірю7.Гіпотенуза
більша за будь-який
катет
20.
Вірю чи не вірю8.Відношення протилежного
катета до гіпотенузи в
прямокутному трикутнику
називається тангенсом кута
21.
Вірю чи не вірю9. Розв'язати прямокутний
трикутник означає знайти його
всі сторони і кути за відомими
сторонами і кутами
22.
Вірю чи не вірю10. Чи дорівнює катет, який
лежить проти кута 30° половині
гіпотенузи
23.
Тестові завданняІ варіант
1.У прямокутному трикутнику АВС (∠С=90°) знайдіть
∠А, якщо ВС = 3√3, АВ = 6.
А) 30° К) 45° С) 60 Ч) 35°
2. Знайти tg 45°.
А) √3
И) 1 К) √2/2
М) 1/√3
3. Знайдіть синус кута А(∠С=90°), якщо
АВ=6, ВС=3, АС=4.
Н) ½ ; К) 4/6; М) 6/2; В) ¾.
4. Оберіть, який з відрізків зображених на малюнку є
проекцією похилої на пряму a.
У) АВ; У) АВ; Р)АС;
5. Якщо катети прямокутного трикутника дорівнюють
6см і 8см, то його гіпотенуза дорівнює
В) 5 см; Г) 2√7 см; Д) 4√7 см; С) 10 см;
24.
Тестові завданняІІ варіант
1.У прямокутному трикутнику АВС (∠С=90°)
знайдіть АВ, якщо АС = 3, cosA = 1/3.
D) 6; М) 9; К) 8 ; Т) 3;
2. Знайти sin30°. А) √3/2; К) √2/2; С) 1/√3; І) ½;
3. Знайдіть косинус кута А
трикутнику АВС (∠С=90°),якщо АВ=6, ВС=3; АС=4. А)
½; Н) 2/3; В) 6/2; Д) ¾;
4.Оберіть, який з відрізків зображених на малюнку є
перпендикуляром до прямої a.
У) АС; А) ВС; Д) АВ;
5. Якщо гіпотенуза прямокутного трикутника дорівнює
4√3 см, а один з гострих кутів 60°, то катет,
протилежний іншому куту дорівнює
А) √3 см; С) 2√3см; В) 8 см; М) 4 см.
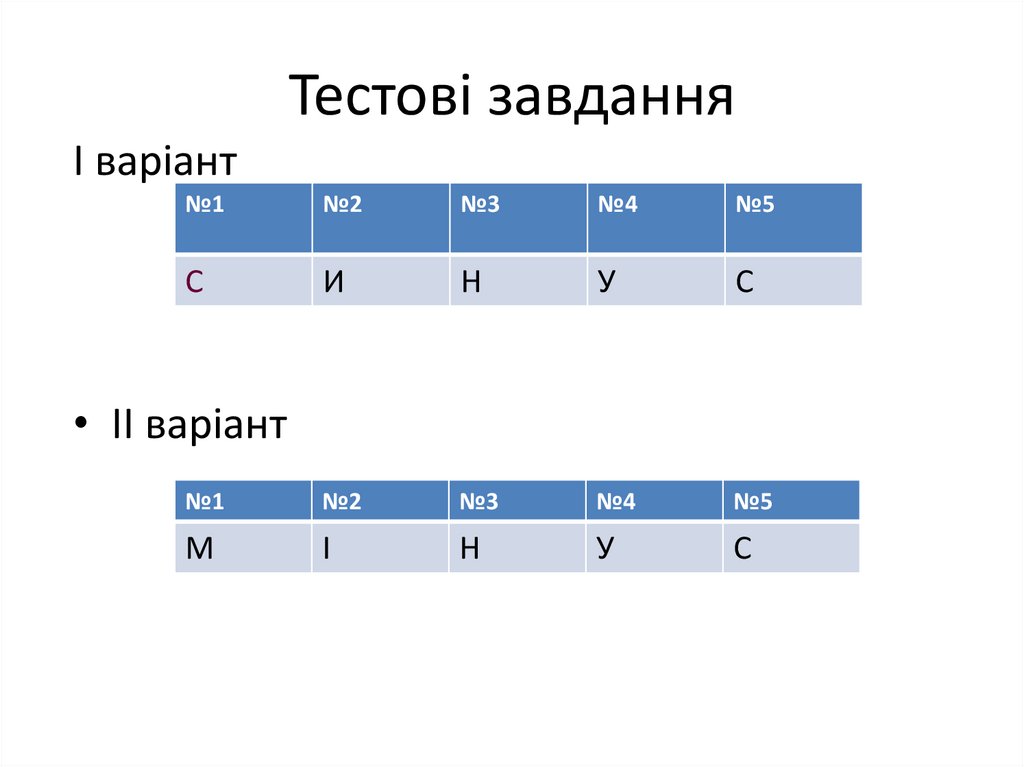
25. Тестові завдання
І варіант№1
№2
№3
№4
№5
С
И
Н
У
С
№1
№2
№3
№4
№5
М
І
Н
У
С
• ІІ варіант
26.
Пасажирський літак, який перебуває надпунктом А на висоті 400м, почав посадку на
злітну смугу аеродрому. Знайдіть кут α
приземлення літака, якщо аеродром
знаходиться на відстані 1,2 км від пункту А
С
В
α
А
Розв’язання:
АС=400м
АВ=1,2км=1200м
tgα=FC:AB=400:1200=1/3=0,3333
α=18
27. «Пізанська вежа»
556
• Визначити кут нахилу
вежі, якщо нам відома її
висота – 56 м і те, що
вершина
вежі
була
відхилена на відстань
приблизно 5 м від центру
28. Пізанська вежа
АС=5СВ=56
tgВ=АС/СВ=5/56=0,0893
За таблицею Брадіса
В=5
29. “Прилади для вимірювання кутів”
30.
.Теодоліт — прилад для
вимірювання кутів
(горизонтальних і
вертикальних) на
місцевості
31. Астролябія
• Астролябія – стародавній кутомірнийприлад для визначення широти і
довжини в астрономо-геодезичних
вимірах і навігації.
32.
33. Історична довідка
• Історія не зберегла ім’я вченого,який винайшовтранспортир. Можливо цей інструмент в давнині мав
зовсім другу назву. Сучасна назва походить від
французського слова «transporter»,що означає
«переносити»
• –Але давні вчені виконували виміри не тільки
транспортиром, адже він був незручним для вимірів на
місцевості і рішенню задач прикладного характеру.
Винахід першого інструменту,що дозволяв вимірювати
кути на місцевості, зв’язують з іменем давньогрецького
вченого Герона Александрійського(І ст.до н.е.). Він
описав інструмент «діоптр»,що дозволяв вимірювати
кути на місцевості і розв’язувати багато прикладних
задач.
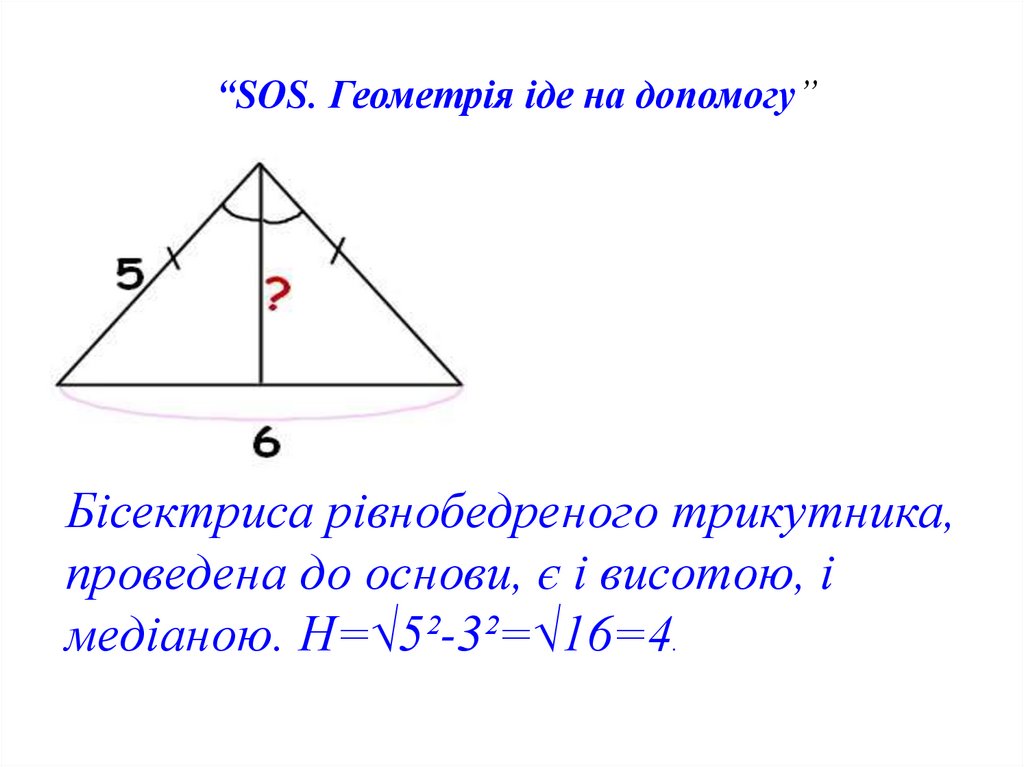
34. “SOS. Геометрія іде на допомогу”
Бісектриса рівнобедреного трикутника,проведена до основи, є і висотою, і
медіаною. Н=√5²-3²=√16=4
.
35. «Допомогла теорема Піфагора». Якої довжини має бути драбина, щоб її можна було приставити до вікна, розташованого на висоті 150
см, якщовідстань від нижнього кінця драбини до
будинку має дорівнювати 200 см?
36. «Допомогла теорема Піфагора»
Розв’язання:АС=200см =2м, ВС=150см=1,5м.
Тоді АВ=√2,25+4=2,5м.
Відповідь: 2,5м
37. «Допомогла теорема Піфагора».
• Покажемо як можна довести за допомогою теореми Піфагора невинністьабо винність підозрюваного. Цей епізод узятий з реальної слідчої практики.
Отримавши повідомлення про крадіжку Шерлок Холмс виїхав на місце
випадку. Заявник стверджував, що злочинець проник в приміщення, де
зберігалися цінності, через вікно. Огляд показав, що підвіконня знаходиться
на відстані 150 см від землі. Поверхня землі на відстані 200 см від стіни
будівлі покрита густою порослю, що не мала жодних слідів пошкоджень.
При огляді не було знайдено жодних технічних засобів типа сходів. Виникло
припущення, що злочинець проникав в приміщення через вікно, якимсь чином
здолавши відстань між зовнішнім краєм поросли і підвіконням. Воно було
визначене за допомогою теореми Піфагора.
38. «Допомогла теорема Піфагора».
Висновок Шерлока: Слідчий висунув версіюпро інсценування кражі,бо драбини коло
вікна не було,а перепригнути через кущі та
допригнути до високого вікна не реально.
39.
• АС=1150м• <А=90 – 9 = 81
• Знайти ВС
ВС=АСхsin81=1150х0,988=1136,2(м)
Відповідь: 1136,2м.
40.
41.
42.
43.
44.
45.
46. Домашнє завдання
• § 17-18 – прочитати та знати відповіді напитання після параграфів
• Законспектувати урок, розібрати усі задачі,
вивчити таблицю значень тригонометричнтих
значень 30, 45, 60 градусів, тригонометричних
тотожностей напам’ять






































 Математика
Математика








