Похожие презентации:
Трикутники
1.
2.
•Розширимо поняття про трикутники,їх види, елементи і властивості;
•Пригадаємо класифікацію трикутників;
Навчимося розв’язувати задачі з
використанням основних властивостей
трикутників.
3.
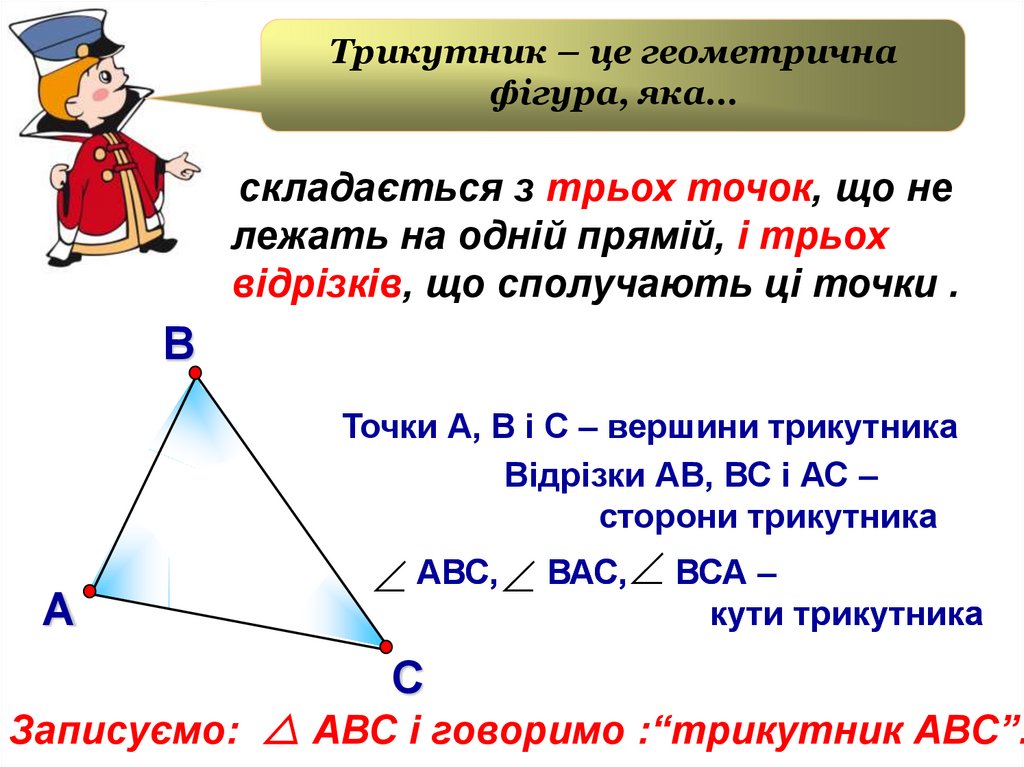
Трикутник – це геометричнафігура, яка…
складається з трьох точок, що не
лежать на одній прямій, і трьох
відрізків, що сполучають ці точки .
В
Точки А, В і С – вершини трикутника
Відрізки АВ, ВС і АС –
сторони трикутника
А
АВС, ВАС, ВСА –
кути трикутника
С
Записуємо: АВС і говоримо :“трикутник АВС”.
4.
Трикутник:А
С
АВ = c,
а
BC = a,
Вершини трикутника
позначаються А, В, С.
В
Сторони
позначаються АВ,
ВС, АС, або
маленькими буквами
а, b ,c , при цьому
дотримуються
правила:
AC = b
5.
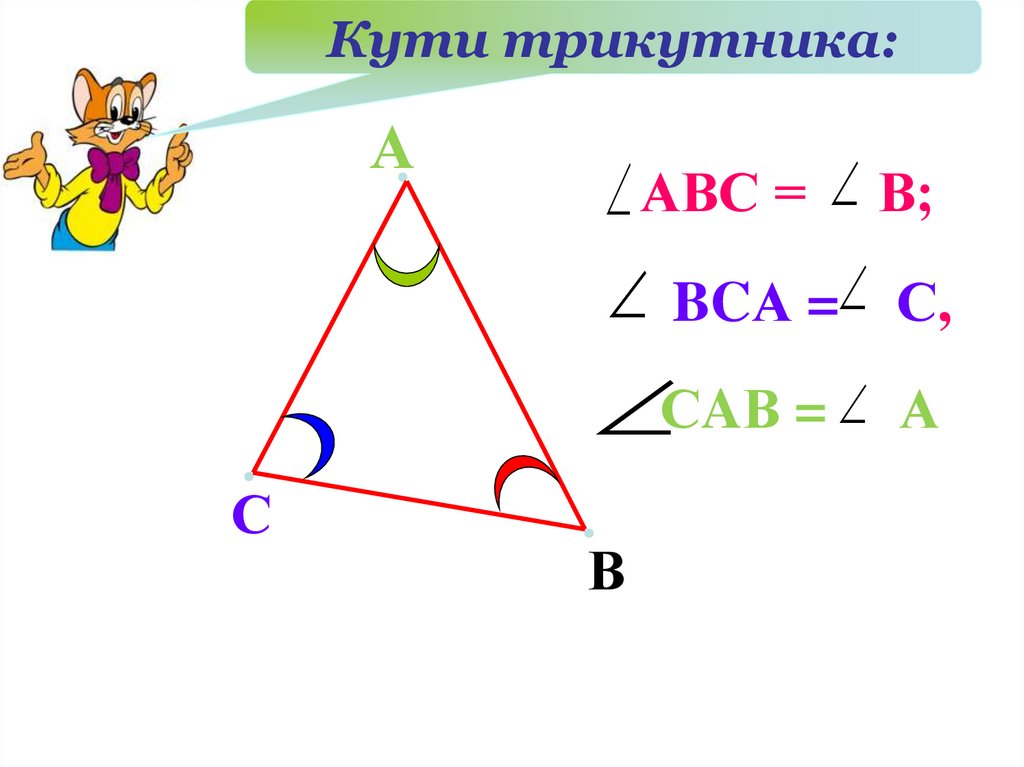
Кути трикутника:А
АВС = В;
BCА = С,
СAВ = А
С
В
6. Назвати трикутники,зобра-жені на малюнку.
Назвати трикутники,зображені на малюнку.1)Яка сторона лежить
проти кута С ?
D
А
2) Назвати сторони,
прилеглі до кута С.
В
С
7. Накреслити довільний трикутник АВС. Назвати:
• сторони,які лежать проти кутівА і В;
• кути, які лежать проти сторін
АВ і ВС ;
• кути, прилеглі до сторони АВ ;
• кут, що лежить між сторонами
АС і ВС.
8. Нерівність трикутника:
Будь-яка сторона трикутника меншавід суми двох інших його сторін.
В
8
5
А
С
11
11 < 5 + 8
АС < АВ + ВС
9.
Чи можуть відрізки бутисторонами трикутника:
1)
3 см
2 см
2)
5 см
3 см
5 см
3)
10 см
7 см
8 см
4)
4 см
7 см
12 см
9 см
10.
Класифікація трикутників:Трикутник
Залежно від довжини сторін
Залежно від міри кутів
різносторонній
гострокутний
рівносторонній
тупокутний
рівнобедрений
прямокутний
11.
Класифікація трикутників:А
С
Е
різносторонні, якщо всі
сторони мають різну
довжину : АВ≠ВС≠АС
рівносторонні, якщо всі
В
сторони рівні : KE = EF
К
= KF
F
N
рівнобедрені, якщо дві
сторони рівні .Рівні сторони
рівнобедреного трикутника
називаються бічними сторонами, а
третя сторона – основою
12.
АКласифікація трикутників:
госторокутні, якщо всі
кути гострі : < A < 900 ,
< B < 900 , <C < 900
С
В
Е
F
D
катет
К
тупокутні , якщо один з
кутів тупий : < E > 900.
прямокутні, якщо один
з кутів прямий : < M =900
катет
N
13.
Прямокутний трикутник:ВС= а – катет, АС=в – катет,
А
АВ=с – гіпотенуза.
Катети – це сторони, що
катет
утворюють прямий кут, а
гіпотенуза – це сторона, яка
лежить напроти прямого кута.
С
У прямокутному трикутнику АВС
прийнято прямий кут позначати
кут С (∟С = 90º), а гіпотенузу - с.
катет
В
14.
ВВизначити вид трикутника:
Дано:АВ = 4 см, ВС = 6 см, АС = 8см
АВС -різносторонній
С
А
Р
К
М
Дано:КР = РТ = КТ = 12 см
КРТ - рівносторонній
Т
Дано:ОМ = МД = 24см, ОД = 4см
ОМД – рівнобедрений
ОМ, МД – бічні сторони
О
Д
ОД - основа
15.
1) À 450 , Â 750 , Ñ 600- гострокутний
АВС
А 90 , B 90 , C 90
0
0
0
2) M 150 , N 250 , Ä 1400
ДMN- тупокутний
М 900 , N 900 , Д 900
3) Ê 900
EKF
- прямокутний
E 90 , F 90
0
0
16.
Уже кілька тисяч років тому єгиптяни знали, що коли сторонитрикутника дорівнюють 3, 4 і 5 одиничним відрізкам, то такий
трикутник прямокутний.
Землеміри Стародавнього Єгипту для побудови прямого кута ділили
мотузку вузликами на 12 рівних частин і кінці зав’язували. Потім
мотузку розтягували на землі так, щоб утворився трикутник зі
сторонами по 3, 4 і 5 поділок. Більший з кутів утвореного
трикутника – прямий. Ребра бічних граней єгипетських пірамід
утворюють майже рівносторонні трикутники.
17.
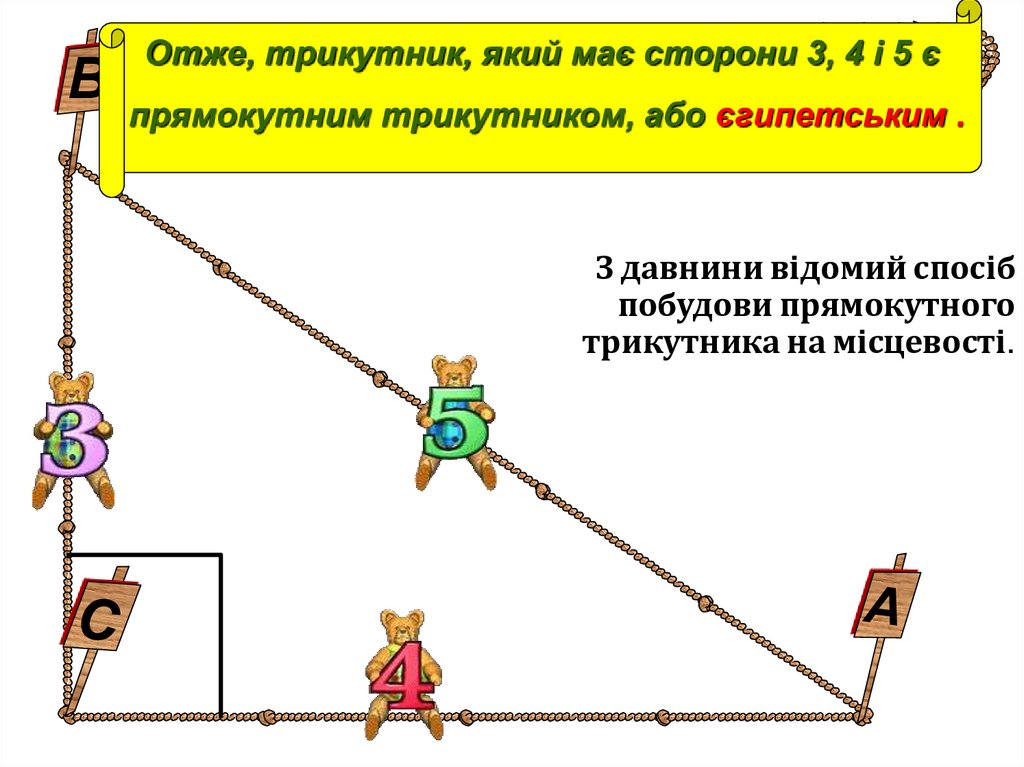
Отже, трикутник, який має сторони 3, 4 і 5 єВ прямокутним трикутником, або єгипетським .
З давнини відомий спосіб
побудови прямокутного
трикутника на місцевості.
18.
ВЦей спосіб використовували в давнину
при будівництві пірамід.
19. Периметр трикутника
Суму довжин усіх сторін трикутниканазивають його периметром.
Периметр позначають буквою Р.
Те, що периметр трикутника АВС
дорівнює 50 см, коротко можна
записати так:
= 50см.
ABC
P
P ABC = AB + BC + AC
20.
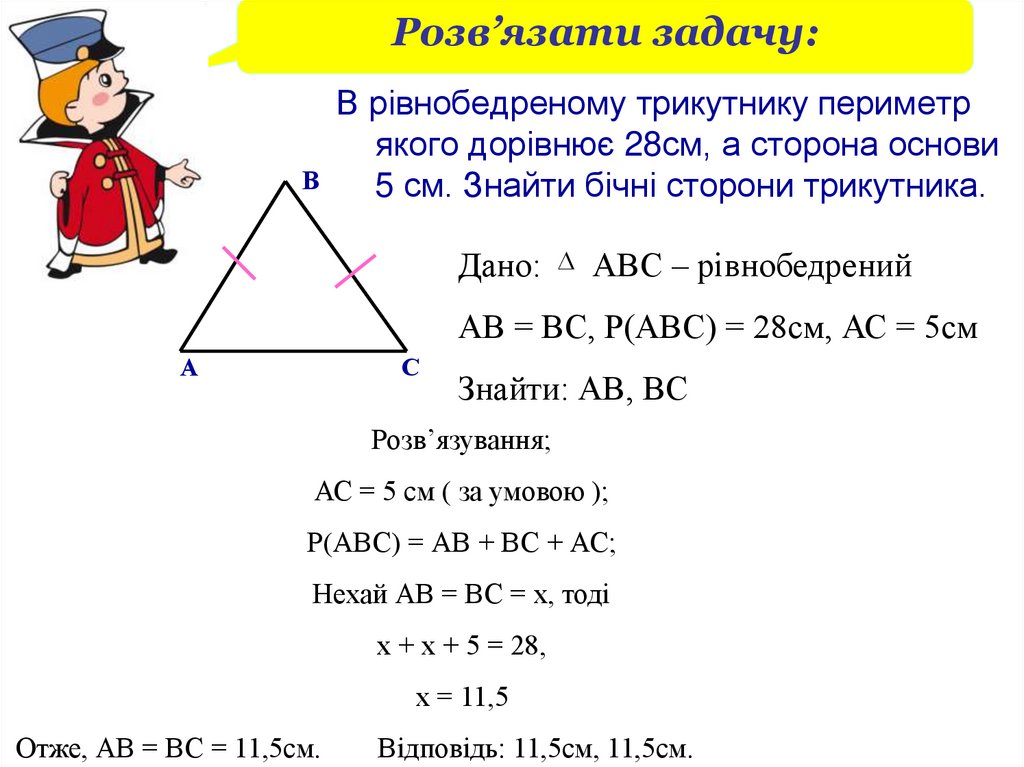
Розв’язати задачу:В рівнобедреному трикутнику периметр
якого дорівнює 28см, а сторона основи
В
5 см. Знайти бічні сторони трикутника.
Дано: АВС – рівнобедрений
АВ = ВС, Р(АВС) = 28см, АС = 5см
А
С
Знайти: АВ, ВС
Розв’язування;
АС = 5 см ( за умовою );
Р(АВС) = АВ + ВС + АС;
Нехай АВ = ВС = х, тоді
х + х + 5 = 28,
х = 11,5
Отже, АВ = ВС = 11,5см.
Відповідь: 11,5см, 11,5см.
21.
Розв’язати задачу:В
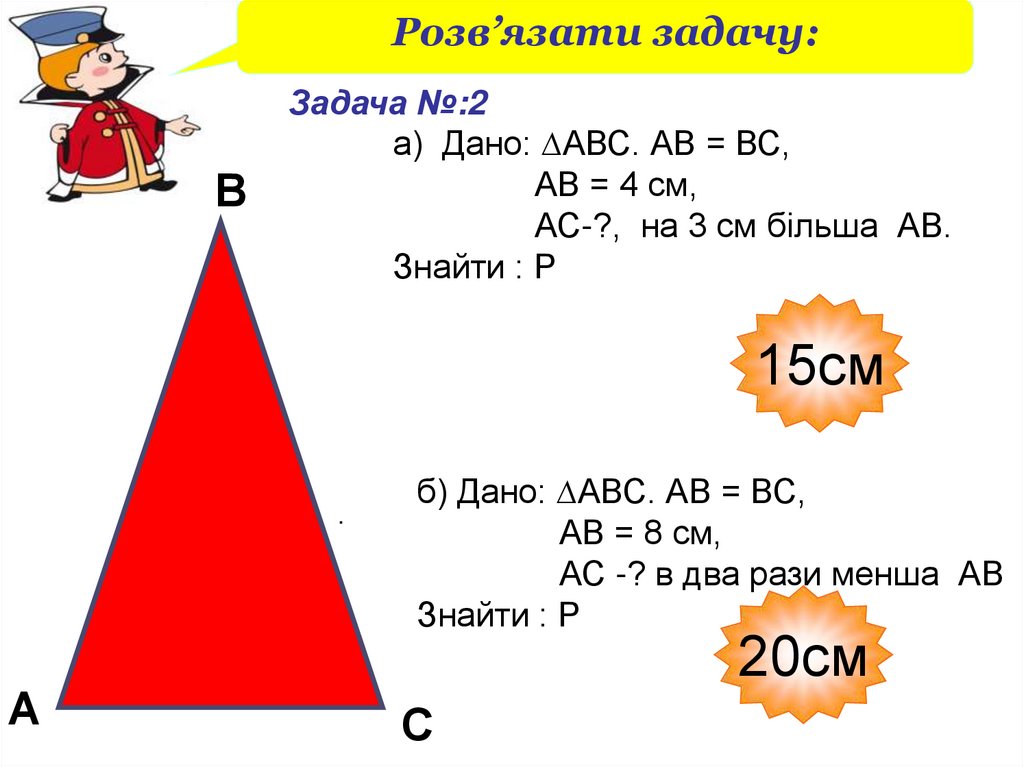
Задача №:2
а) Дано: ∆АВС. АВ = ВС,
АВ = 4 см,
АС-?, на 3 см більша АВ.
Знайти : Р
15см
.
А
б) Дано: ∆АВС. АВ = ВС,
АВ = 8 см,
АС -? в два рази менша АВ
Знайти : Р
20см
С
22.
Розв’язати задачу:Задача№:3
В
а) Дано:
∆АВС:
49см,
г)Дано
: ∆АВС
, РР==40
см
=2
ВС;
= 12 АС
см. ,
АВ- АВ
? на
смАС
менша
Знайти
: АВ,
АС-?
наВС
3 см менша ВС
14см
б)
Дано
:
∆АВС
,
Р
=
40
см
Знайти: АВ,ВС
АВ : ВС : АС = 2 : 2 : 4.
10см, 10 см
Знайти: АВ,ВС, АС
20см
в) Дано : ∆АВС , Р = 40 см
11см, 13 см
АВ : ВС : АС = 2 : 3 : 5. 16см
8см, 12 см
Знайти: АВ,ВС
20см
А
С
23.
Давайте пригадаємо:Що таке трикутник ?
Сформулюйте нерівність трикутника.
Як називають трикутники залежно від довжин їх
сторін?
Як називаються трикутники залежно від міри кутів ?
Як називаються сторони рівнобедреного трикутника?
Як називають сторони прямокутного трикутника?
Який трикутник називається рівностороннім?
Що таке периметр трикутника?
24.
Повторимо:Трикутник – це геометрична
фігура, яка…
ABC
В
Точки А, В і С – вершини трикутника
Відрізки АВ, ВС і АС –
сторони трикутника
АВС, ВАС, ВСА –
кути трикутника
Р = АВ + ВС + АС
периметр трикутника
А
С


















 Математика
Математика








