Согласованность оценивания работ

1.

Согласованность оценивания
работ

2.

Общие положения
• Читаем внимательно, наличие следов
решения должно быть оценено баллами.
• В противном случае выставляется «Не
приступал».
• При неверном ответе полный балл
выставлять нельзя.

3.

Задание 12. Общие замечания
1 балл
Верно решен пункта), в пункте б)
- на тригонометрической окружности не обозначен
промежуток из условия задачи;
- на тригонометрической окружности не установлено
соответствие между обозначенными точками и
найденными решениями;
- при отборе корней «организованным перебором» не
доказано отсутствие корней из данного промежутка при
других значениях целочисленного параметра;
- при решении двойного неравенства допущена ошибка;
В решении пункта а) присутствует вычислительная ошибка,
но последующее решение содержит верную
последовательность всех шагов решения обоих пунктов.

4.

0 баллов
- при переносе слагаемого в другую часть
уравнения его знак не поменяли
- неверно применена тригонометрическая
формула
- ошибка в формуле корней простейшего
тригонометрического уравнения
- неверно найдено значение
арккосинуса/арксинуса числа
- неверно решено квадратное уравнение

5.

Задание 12 (вариант 505)

6.

Задание 12 (вариант 111)

7.

Наиболее распространённые ошибки в 12(а).
• ОДЗ указана, но допущены ошибки в
решении. ДОПУСКАЕТСЯ написать ОДЗ, но
не находить.
• Преобразование тригонометрических
выражений.
• Запись серий корней: неверно указан
период; неверно найдено начальное
значение.

8.

При отборе корней в 12(б)
Для тригонометрической окружности:
-дуга обозначена любым способом, концы указаны
верно;
-есть соответствие корней и изображающих их точек;
-правильность вычислений.
Для отбора корней методом организованного
перебора для каждой серии есть «недолёт» и
«перелёт».
Для отбора корней с помощью двойного неравенства
внимательно проверяем все выкладки.

9.

Задание 14. Общие замечания
1 балл
Получен неверный ответ из-за вычислительной ошибки в результате
выполнения действия …., при этом имеется верная последовательность
всех шагов решения.
0 баллов
(1) Не найдена /не учтена/ область допустимых значений переменной;
ответ неверный, так как в ответ вошли точки, не являющиеся решением
неравенства.
(2) Выписаны не все неравенства для поиска ОДЗ (при наличии
аббревиатуры ОДЗ)
(3) Допущена ошибка в ходе преобразовании рационального выражения,
не являющаяся вычислительной.
(4) При решении неравенства методом интервалов неверно расставлены
знаки на числовой прямой.
(5) При решении неравенства перебором знаков множителей
рассмотрены не все возможные случаи
(6) Выполнен неравносильный переход от строки к строке.
(7) неверно выписаны/преобразованы ограничения на область
допустимых значений переменной

10.

Задание 14 (вариант 111)

11.

• Проверка правильности ответа.
• Если написано ОДЗ, то указываются все
условия.

12.

Задание 14 (вариант 505)

13.

Решение неравенства осуществляется
введением новой переменной и сведением
его к рациональному неравенству. Важно:
рациональное неравенство должно быть
решено верно. Если на новую переменную
введено ограничение, то его нужно
учитывать. На координатной прямой
отмечено верное решение рационального
неравенства: учтено введенное t>0 или
выколота точка 0. Примеры:

14.

2 балла

15.

0 баллов

16.

Преобразование показательного выражения, в
ходе которого числитель и знаменатель дроби
умножаем на 2х, считаем равносильным. Если
далее произвести замену переменной и
решить рациональное неравенство, то
выкалывать 0 не нужно.
Вывод: в ходе проверки нужно отслеживать, в
какой момент произведена замена
переменной, в зависимости от этого проверять
правильность решения рационального
неравенства. Требование t>0 не является
обязательным.

17.

Допустима рационализация
2 балла

18.

Задание 15. Общие замечания
1 балл
(1) Обоснованно составлена математическая модель,
в решении уравнения допущена ошибка
(2) Обоснованно составлена математическая модель,
решение уравнения отсутствует.
0 баллов
- Математическая модель отсутствует, так как нет
описания переменной.
- В решении задания нет соответствия между
единицами измерения.
- При решении задачи арифметическим способом
допущена вычислительная ошибка, математическая
модель не построена.

19.

Задание 15 (вариант 111)

20.

Задание 15 (вариант 505)

21.

Общие положения
• Описаны все переменные
• Указано, на сколько ежемесячно
уменьшается долг: S/n или введена
специальная переменная
• Таблица составлена правильно: заголовки
верны, строки читаемы (количество строк в
1 и последнем столбце одинаково, можно
установить соответствие в записях)
• Выражения в столбцах не содержат ошибок
• Запись r%/100 ошибочна

22.

0 баллов

23.

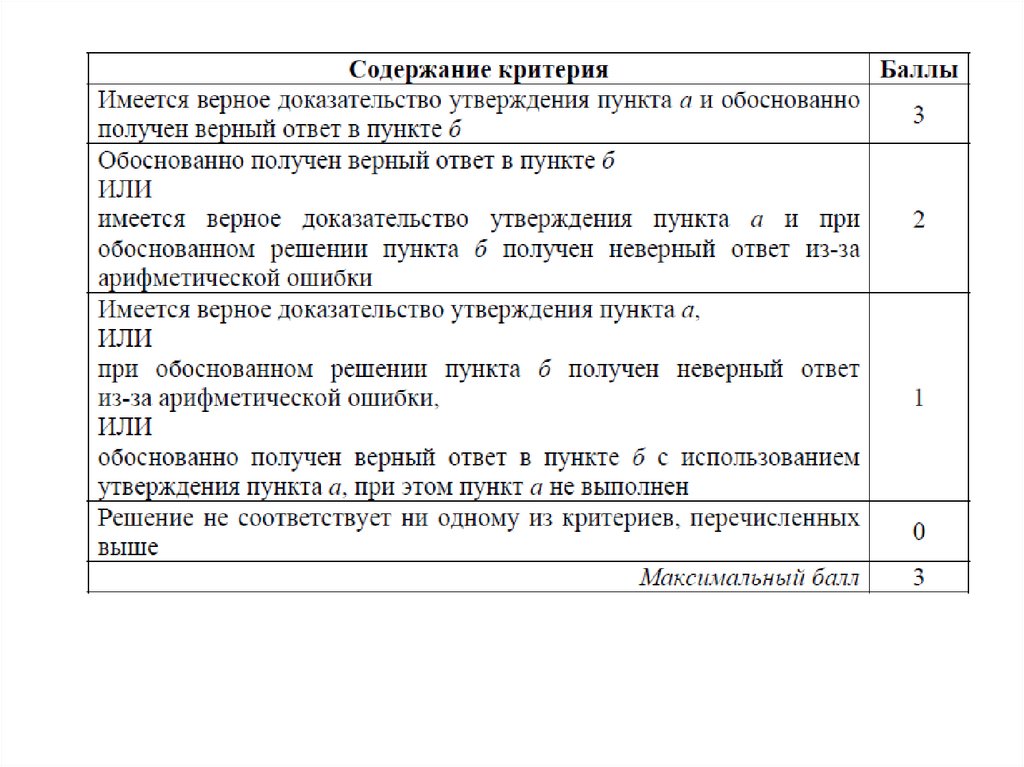
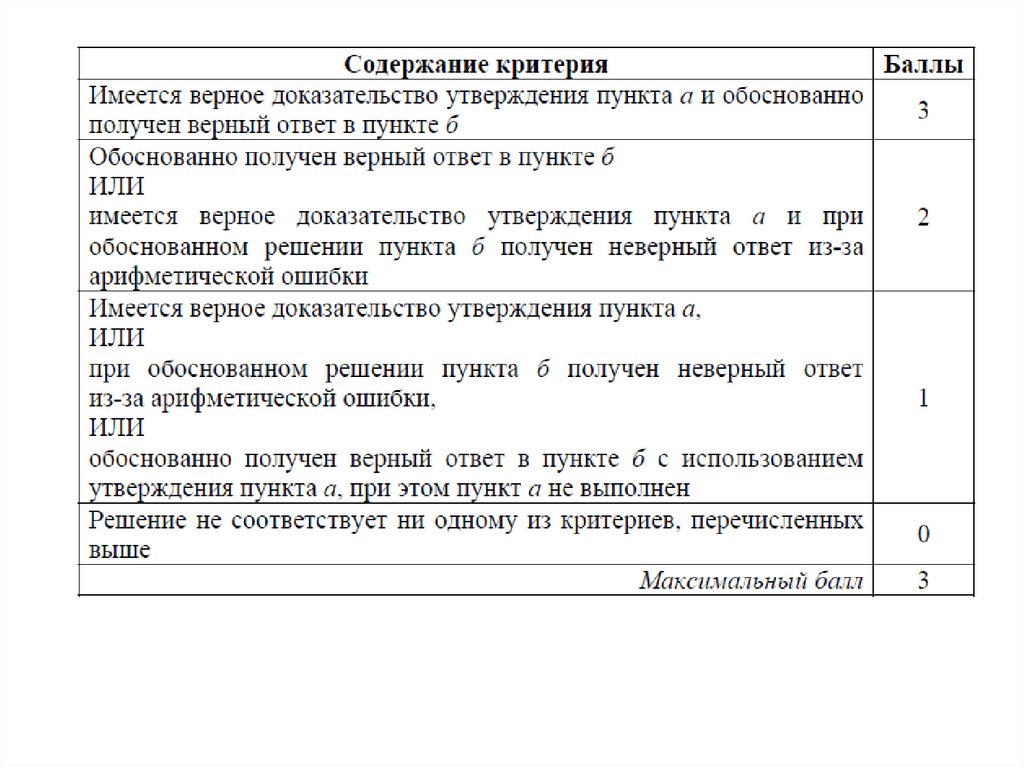
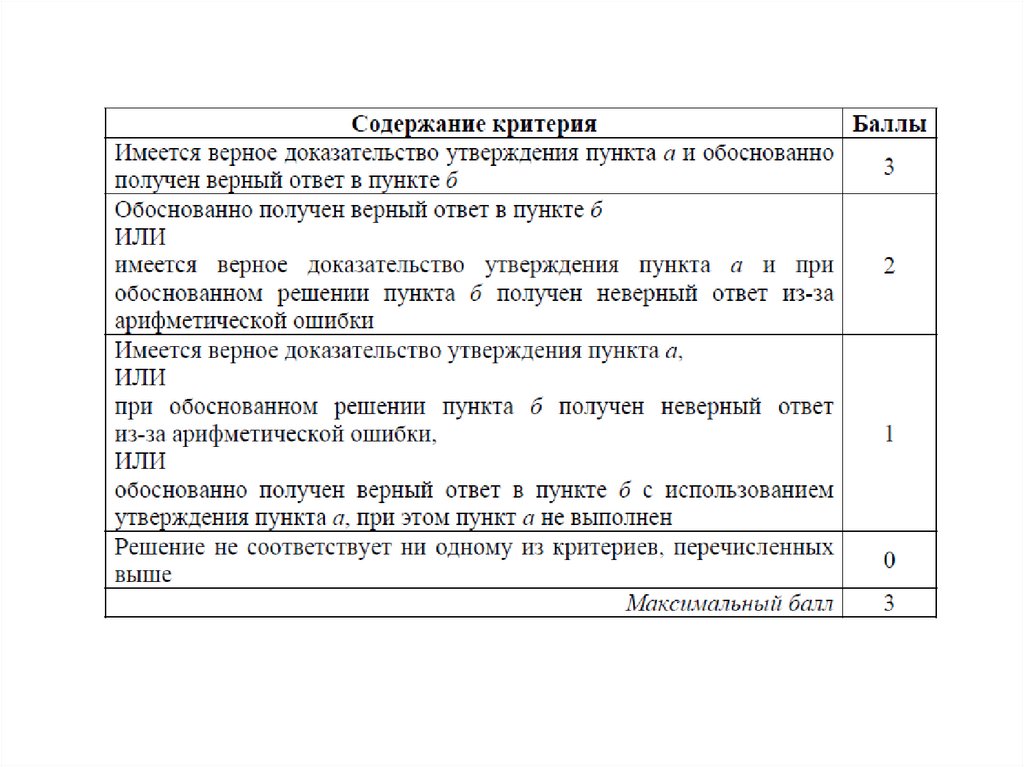
Задание 13. Общие замечания
2 балла
(1) В решении приведено верное доказательство утверждения пункта а).
(2) Все шаги решения пункта б) присутствуют, получен неверный ответ из-за
вычислительной ошибки.
(3) Доказательство утверждения пункта а) отсутствует, в пункте б) обоснованно
найден верный ответ.
(4) В пункте б) обоснованно получен правильный ответ без использования
утверждения пункта а).
Ошибки п. а)
(1) При решении задачи координатно-векторным способом неверно определены
координаты точки
(2) При решении задачи координатно-векторным способом неверно определены
координаты вектора
(3) При доказательстве утверждения координатно-векторным способом
допущена ошибка в формуле косинуса угла между прямыми: потерян знак
модуля в числителе.
(4) При доказательстве утверждения координатно-векторным способом
допущена ошибка в формуле косинуса угла между векторами: в числителе
стоит знак модуля.
(5) В доказательстве утверждения п. а) неверно применена теорема о трёх
перпендикулярах.

24.

1 балл
(1)В решении приведено верное доказательство утверждения пункта а).
Решение пункта б) отсутствует.
(2)В решении приведено верное доказательство утверждения пункта а).
При выполнении пункта б) …
- координатно-векторным способом допущены ошибки в формуле
расстояния от точки до плоскости;
- не доказано, что построенный отрезок является перпендикуляром к
плоскости;
- не доказано, что построенный отрезок является расстоянием от точки до
плоскости;
- допущена ошибка в формуле объёма пирамиды (не является
вычислительной);
- допущена ошибка при выражении высоты из формулы объёма
пирамиды.
В решении отсутствует доказательство утверждения пункта а), при
выполнении п. б) допущена вычислительная ошибка при нахождении
Доказательство утверждения п. а) содержит ошибки …, при выполнении
пункта б) допущена вычислительная ошибка при нахождении …

25.

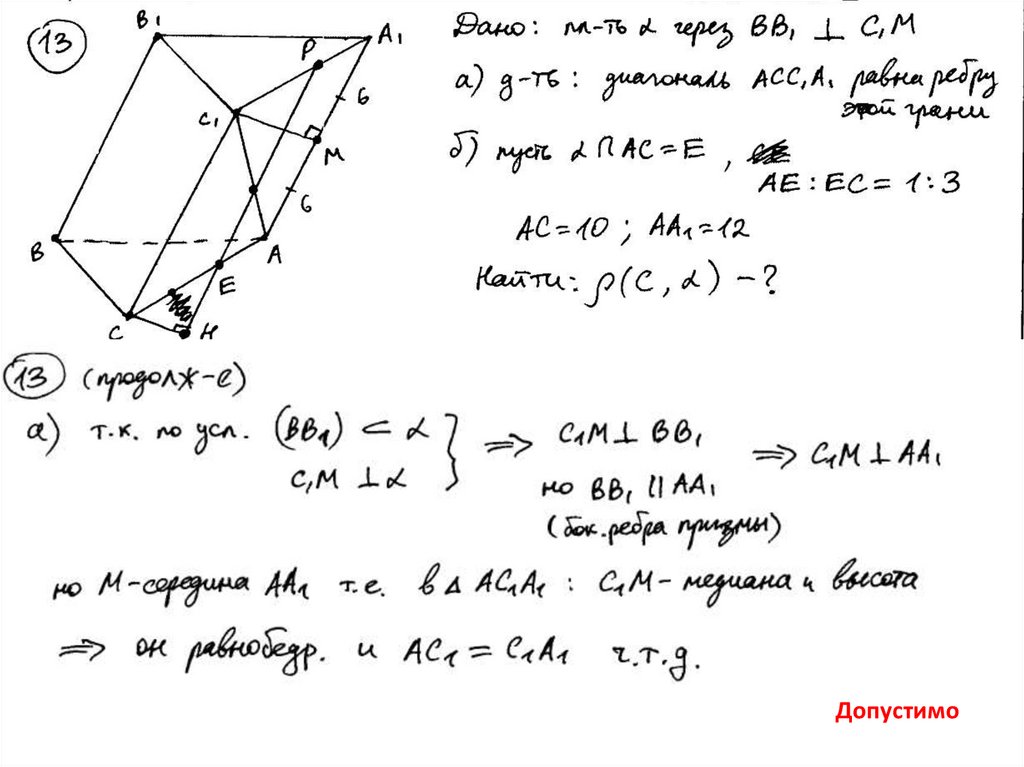
Задание 13 (вариант 111)

26.

Задание 13 (вариант 505)

27.

28.

Требует внимания при проверке
• Внимательно читаем утверждения
• Рассуждения должны содержать грамотные
обоснования
• В тексте указываются те объекты, о которых
идет речь, описки недопустимы

29.

Допустимо

30.

Задание 16. Общие замечания
2 балла
(1) В решении приведено верное доказательство
утверждения пункта а).
Все шаги решения пункта б) присутствуют, получен
неверный ответ из-за вычислительной ошибки при
нахождении ….
(2) Доказательство утверждения пункта а) отсутствует,
в пункте б) обоснованно найден верный ответ без
использования утверждения пункта а).
(3) Доказательство утверждения пункта а) нельзя
считать верным (обоснованным), так как …
В пункте б) обоснованно получен правильный ответ
без использования утверждения пункта а).

31.

1 балл
• В решении приведено верное доказательство утверждения пункта а).
Решение пункта б) отсутствует.
• В решении приведено верное доказательство утверждения пункта а).
При выполнении пункта б) допущены ошибки, не являющиеся
вычислительными
• Доказательство утверждения пункта а) отсутствует, в пункте б)
обоснованно найден верный ответ с использованием утверждения
пункта а).
• Доказательство утверждения пункта а) нельзя считать верным
(обоснованным), так как …
В пункте б) обоснованно найден верный ответ с использованием
утверждения пункта а).
• Доказательство утверждения пункта а) отсутствует, решение пункта б)
выполнено без использования утверждения пункта а), но получен
неверный ответ из-за вычислительной ошибки при нахождении ….
• Доказательство утверждения пункта а) нельзя считать верным
(обоснованным), так как …
Решение пункта б) выполнено без использования утверждения пункта
а), но получен неверный ответ из-за вычислительной ошибки при
нахождении ….

32.

Задание 16 (вариант 111)

33.

34.

Требует внимания при проверке
• Рассмотрены все возможные случаи
положения точек
• Решение полностью обосновано, не
содержит математических ошибок

35.

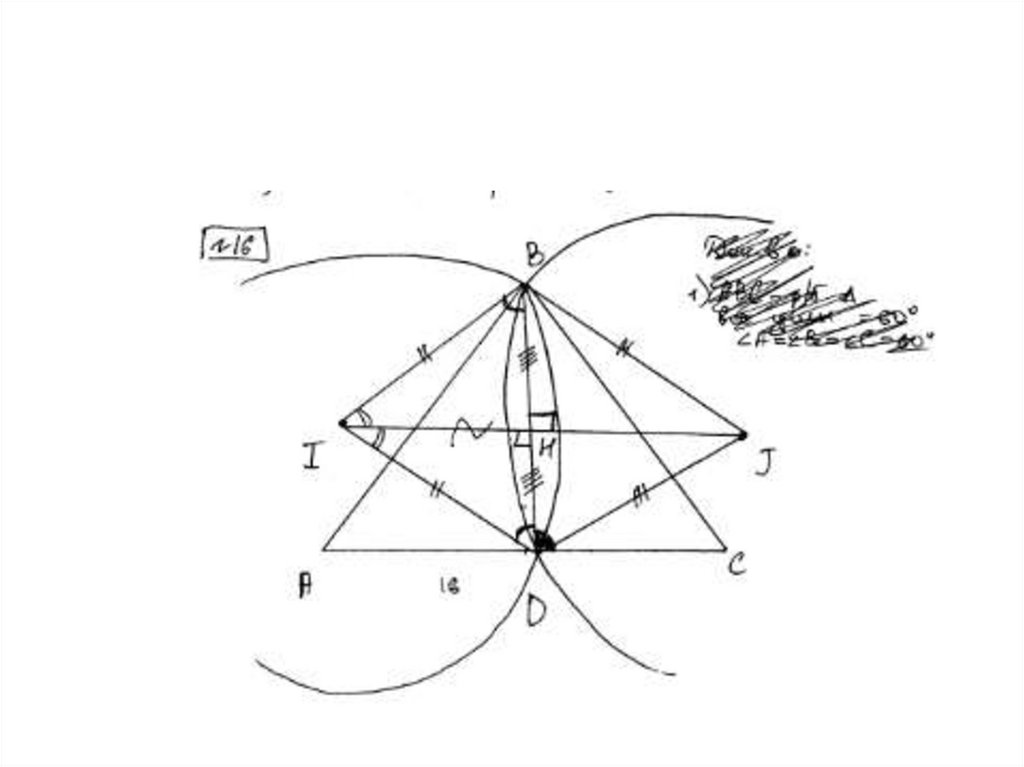
Задание 16 (вариант 505)

36.

37.

Требует внимания при проверке
• Перпендикулярность линии центров общей хорде
должна быть прописана, а не обозначена на рисунке
• Для доказательства пункта (а) положение точек центров
могут быть отмечены неверно (след. слайд)
• Если указано равенство конкретных углов с
обоснованием, что они опираются на одну дугу,
принимаем. Ошибочно общее утверждение: «Углы
равны, так как опираются на одну дугу».
• Внимательно читаем название углов
• Все утверждения должны быть обоснованы
• Наличие математических ошибок не позволяет
выставить балл за решение

38.

39.

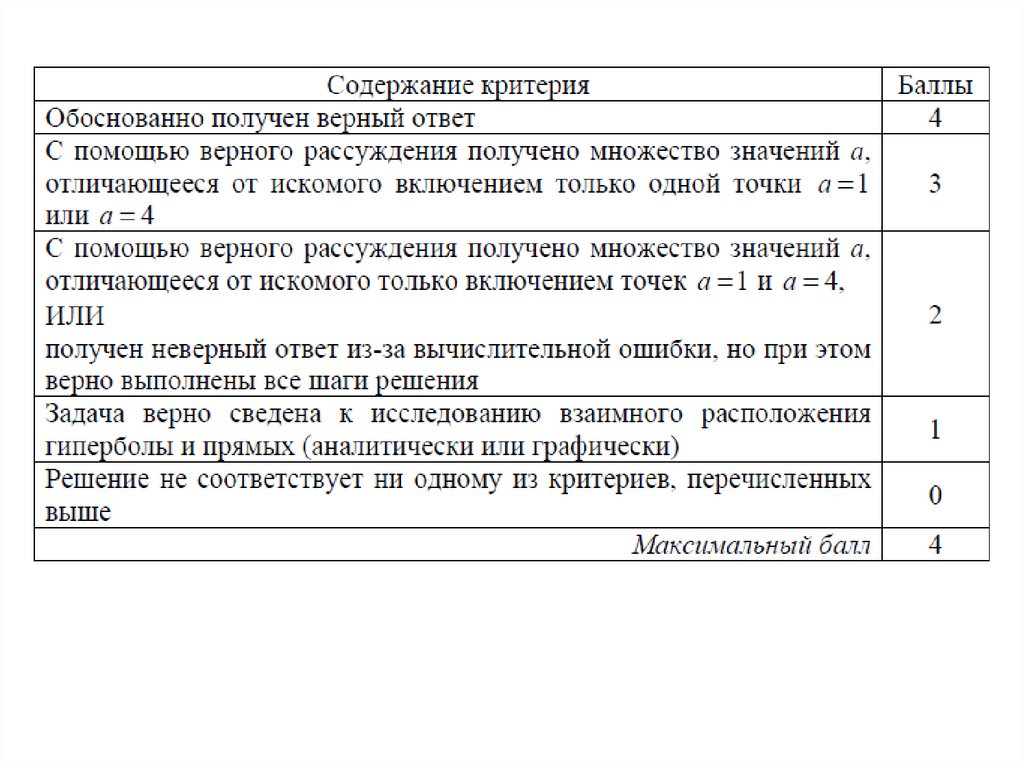
Задание 17. Общие замечания
3 балла
• Приведено полное обоснованное решение, дан ответ,
отличающийся от верного включением/исключением точки …
2 балла
• Приведено полное обоснованное решение, дан ответ,
отличающийся от верного включением/исключением точек …
• Все шаги решения выполнены, но допущена вычислительная
ошибка
• Задача верно сведена к исследованию взаимного
расположения… и найдены граничные значения параметра,
решение задачи не завершено.
• Задача верно сведена к исследованию взаимного
расположения… и найдены граничные значения параметра,
промежутки искомых значений параметра составлены
ошибочно.

40.

1 балл
Для графического метода.
-Верно раскрыт модуль, построены графики и
задача сведена к исследованию их взаимного
расположения, решение задачи не завершено.
- Верно раскрыт модуль, построены графики и
задача сведена к исследованию их взаимного
расположения, граничное значение параметра
найдено неверно.
- Верно раскрыт модуль, построены графики и
задача сведена к исследованию их взаимного
расположения, отсутствует обоснование
граничных значений параметра и выбора
промежутков значения параметра.

41.

1 балл
Для аналитического метода.
• Задача верно сведена к исследованию …: выписаны два
квадратных уравнения при условии
неотрицательности правой части и упоминается
положительность их дискриминантов. Решение задачи не
завершено.
• Задача верно сведена к исследованию …: выписаны два
квадратных уравнения, полученных при раскрытии модуля с
учетом знака подмодульного выражения, и упоминается
положительность их дискриминантов. Решение задачи не
завершено.
• В ходе решения рассмотрены не все случаи
• Верно раскрыт модуль при условии неотрицательности правой
части, задача сведена к исследованию корней квадратного
трёхчлена на промежутке. Решение задачи не завершено.
• Верно раскрыт модуль с учетом знака подмодульного
выражения, задача сведена к исследованию корней
квадратного трёхчлена на промежутке. Решение задачи не
завершено.

42.

0 баллов
-Не учитываются условия раскрытия модуля.
-При раскрытии модуля допущены ошибки…
-Верно раскрыт модуль, но исследование не начато.
- В решении отсутствует сведение к исследованию
взаимного расположения графиков
Для графического метода.
-Верно раскрыт модуль, график построен ошибочно.
-Верно раскрыт модуль, уравнение окружности
неверно преобразовано к каноническому виду.
-Верно раскрыт модуль, неверно определены
координаты центра/радиуса окружности.
-Верно раскрыт модуль, при определении
характеристик «ломаной» параболы допущены
ошибки.

43.

Задание 17 (вариант 111)

44.

45.

Задание 17(вариант 505)

46.

47.

Типичные ошибки
• В качестве ОДЗ указано условие на правую
часть уравнения.
• Не рассматривается случай совпадения
корней

48.

Ошибка
Допустимо

49.

Задание 18 (вариант 506)

50.

Задание 18. Общие замечания
Пункт а)
• Приведённый пример содержит
вычислительную ошибку.
• Пример явно не получен, описывается только
возможность получения числа.
• Решение пункта а) не содержит примера числа в
явном виде, доказательство его существования
проведено с использованием уравнений
относительно буквенных переменных,
обозначающих цифры.

51.

Пункт б)
• Решение строится на построении частного
случая, что не позволяет сделать вывод о том,
что нужного числа не существует.
• Если в решении используется метод перебора, то
он должен быть полным.

52.

Пункт в)
• - при решении пункта в) нет обоснования того,
что результаты применения операции к числам
из разных сотен, различны;
• - при решении пункта в) нет обоснования того,
что все получающиеся результаты различны.

53.

Задание 18

54.

Пункт 18(а)
Проверяем, что приведённый пример
удовлетворяет условиям задачи:
-суммарное количество камней равно
требуемому;
-массы камней в каждой кучке верно
вычислены и удовлетворяют неравенству.

55.

Общее количество камней не удовлетворяет условию (вариант 506, 38 камней)

56.

Пункт 18(б)
• В решении должна присутствовать обоснованность
ограничения камней в первой кучке.
• Если рассматриваются конкретные наборы, то их
должно быть два (при обоснованном ограничении
наибольшего количества камней в первой кучке).
• В решении аргументирован выбор равных масс
камней.
Ошибки.
- Доказательство, что конкретный пример не
удовлетворяет условию.
- Нет попыток оценки выражений.
- Количество камней в 1 и 3 кучках отличается на 2
(на 3), что никак не обосновывается. Доказательство
утверждения ведётся для частного случая.

57.

не рассмотрено 11- 12-15 (вариант 506, 38 камней)
0 баллов

58.

Пункт 18(в)
• Оценка и пример оцениваются независимо.
• Внимательно проверяем оценку, она не
должна сводиться к конкретному примеру
без обоснований.
• Вычисления для конструированного
примера нужно проверять.

59.

Задание 18 (вариант 111)

60.

Задание 18

61.

Пункт 18(а)
Проверяем, что приведённый пример
удовлетворяет условиям задачи:
- числа последовательные;
-сумма дробей равна данному числу.

62.

Числа не являются последовательными

63.

Пункт 18(б)
• В доказательстве рассматривается переход
через десяток, через сотню.
• Перебор случаев обоснован.

64.

Не доказано

65.

не рассмотрено 11- 12-15 (вариант 506, 38 камней)
0 баллов

66.

Пункт 18(в)
• Пункт оценивается неделимо.
• Все утверждения должны быть полностью
обоснованы.
• Доказано, что числа должны быть из
разных сотен.