Похожие презентации:
Определенный интеграл
1. Интегральное исчисление
2. Определенный интеграл
3.
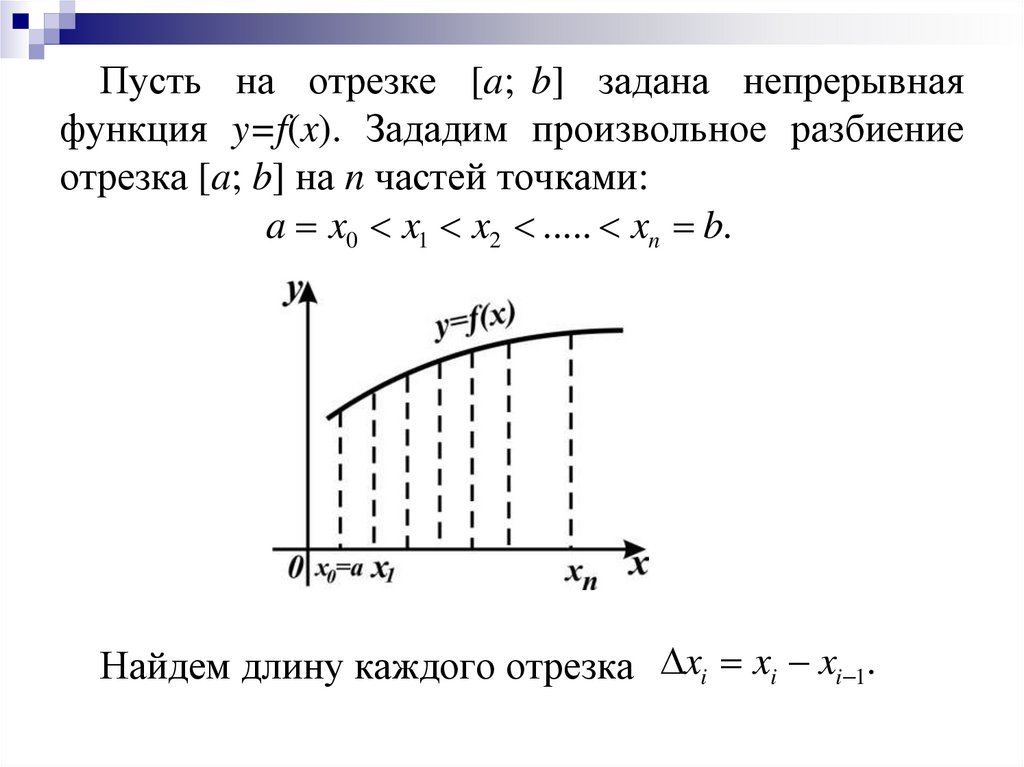
Пусть на отрезке [a; b] задана непрерывнаяфункция y=f(x). Зададим произвольное разбиение
отрезка [a; b] на n частей точками:
a x0 x1 x2 ..... xn b.
Найдем длину каждого отрезка xi xi xi 1.
4.
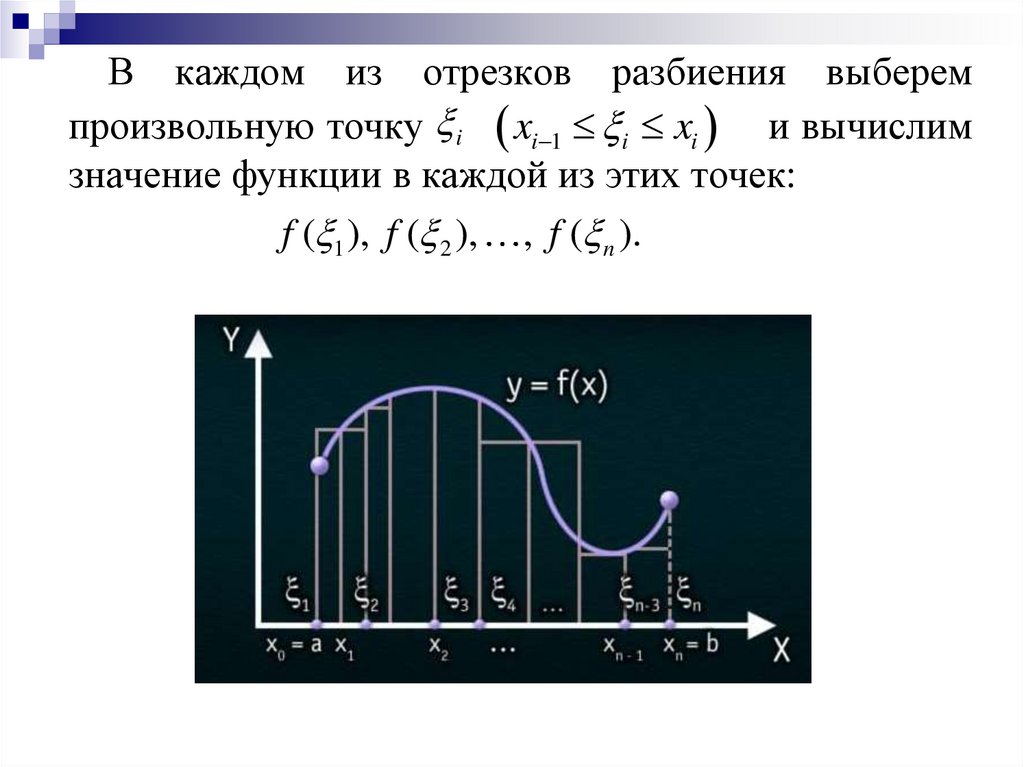
В каждом из отрезков разбиения выберемпроизвольную точку i xi 1 i xi и вычислим
значение функции в каждой из этих точек:
f ( 1 ), f ( 2 ), , f ( n ).
5.
Составим сумму вида:Sn f ( 1 ) x1 f ( 2 ) x2
n
f ( n ) xn f ( i ) xi .
i 1
Сумма Sn называется интегральной суммой для
функции y=f(x) на отрезке [a; b].
Сумма Sn зависит от способа разбиения отрезка
[a; b] на отрезки xi 1 , xi и от выбора точки i внутри
каждого отрезка.
6.
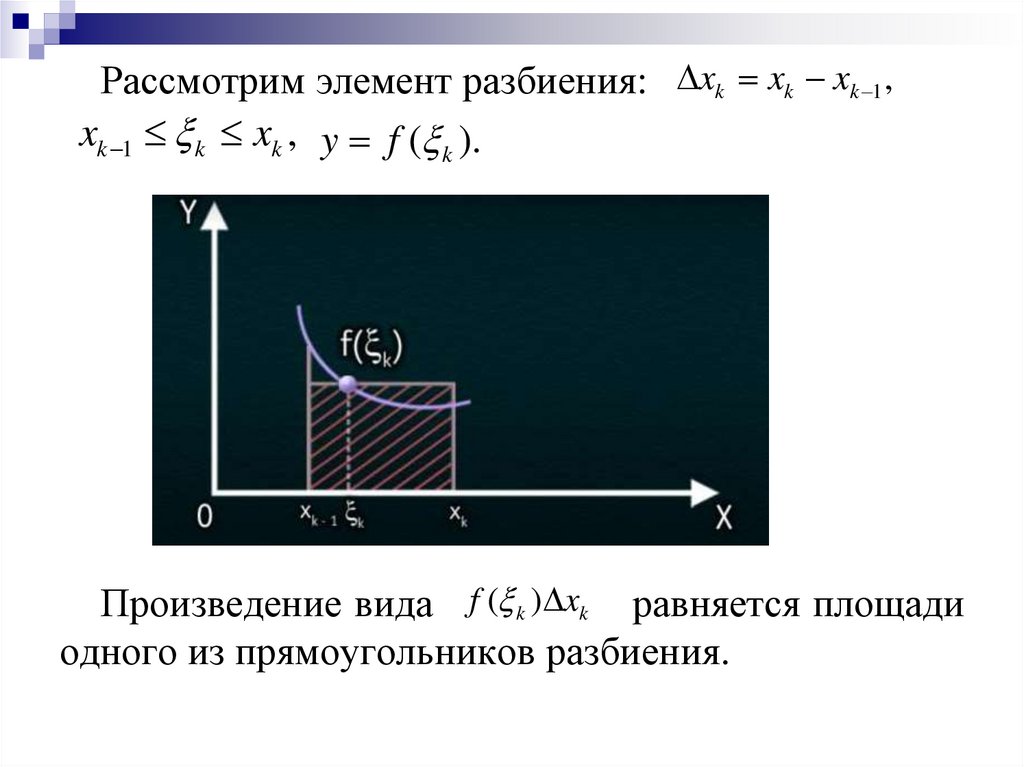
Рассмотрим элемент разбиения: xk xk xk 1 ,xk 1 k xk , y f ( k ).
Произведение вида f ( k ) xk равняется площади
одного из прямоугольников разбиения.
7.
Такимобразом,
геометрический
смысл
интегральной суммы состоит в том, что она
выражает площадь некоторой ступенчатой фигуры.
Зададим разбиения таким образом, чтобы
max xi 0, тогда число отрезков разбиения будет
стремиться к бесконечности n и составим
интегральную сумму:
Sn f ( i ) xi .
i 1
Предположим,
что
последовательность
интегральных сумм Sn стремится к некоторому
пределу S.
8.
Определение: Если при любом разбиении отрезка[a; b] таком, что max xi 0 и при любом выборе
точек i внутри отрезков xi 1 , xi
интегральная
сумма Sn стремится к одному и тому же пределу S, то
этот предел называют определенным интегралом от
функции y=f(x) на отрезке [a; b] и обозначают:
b
n
f ( x)dx lim f ( ) x .
a
max x 0
i 1
i
i
Числа а и b называют соответственно нижним и
верхним пределами интегрирования, [a; b] – отрезок
интегрирования, х – переменная интегрирования.
9.
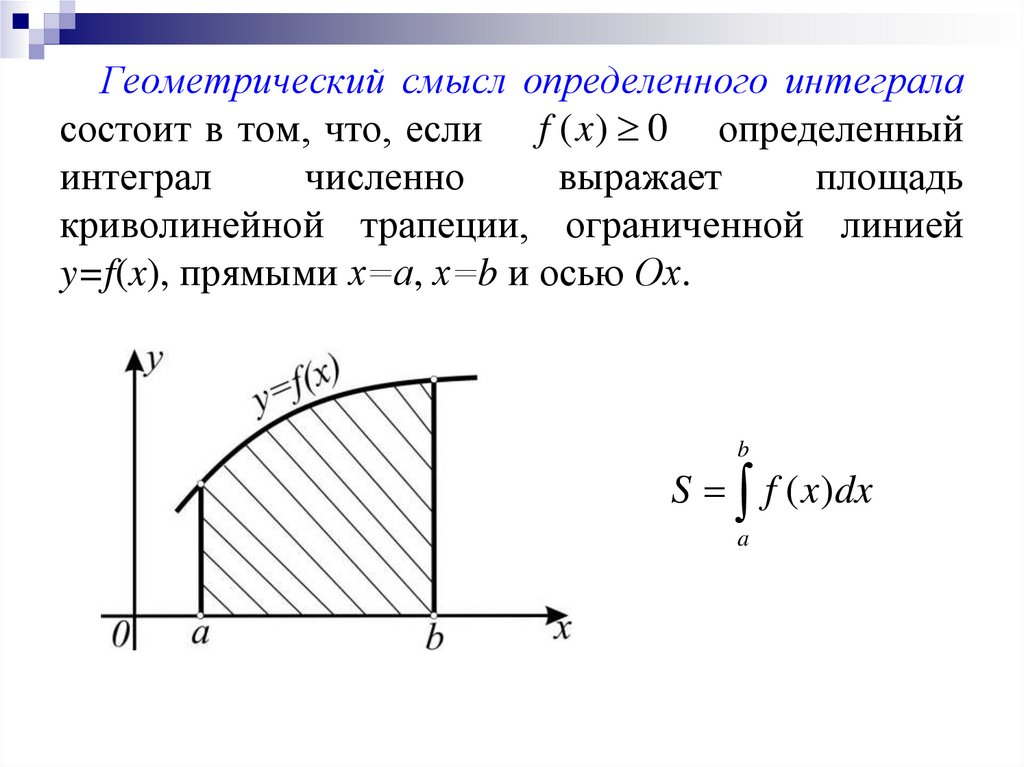
Геометрический смысл определенного интеграласостоит в том, что, если f ( x) 0 определенный
интеграл
численно
выражает
площадь
криволинейной трапеции, ограниченной линией
y=f(x), прямыми х=а, х=b и осью Ох.
b
S f ( x)dx
a
10.
Замечания:1. Определенный интеграл зависит только от вида
функции f(x) и пределов интегрирования, но не
зависит от переменной интегрирования, которую
можно обозначать любой буквой:
b
b
a
a
f ( x)dx f (t )dt
b
f ( z )dz.
a
2. Если в определенном интеграле границы
интегрирования
поменять
местами,
то
определенный интеграл изменит знак:
b
a
a
b
f ( x)dx f ( x)dx.
11. Основные свойства определенного интеграла
1. Постоянный множитель можно выносить зазнак определенного интеграла:
b
b
a
a
C f x dx C f x dx, где С – постоянное число.
2. Определенный интеграл от алгебраической
суммы функций равен алгебраической сумме
интегралов от каждой функции:
b
b
b
a
a
a
f ( x) g ( x) dx f ( x)dx g ( x)dx.
12.
a3. Если а=b, то
f x dx 0.
a
4. Если f(x) – четная функция, то
a
a
a
0
f x dx 2 f x dx.
5. Если f(x) – нечетная функция, то
a
f x dx 0.
a
13.
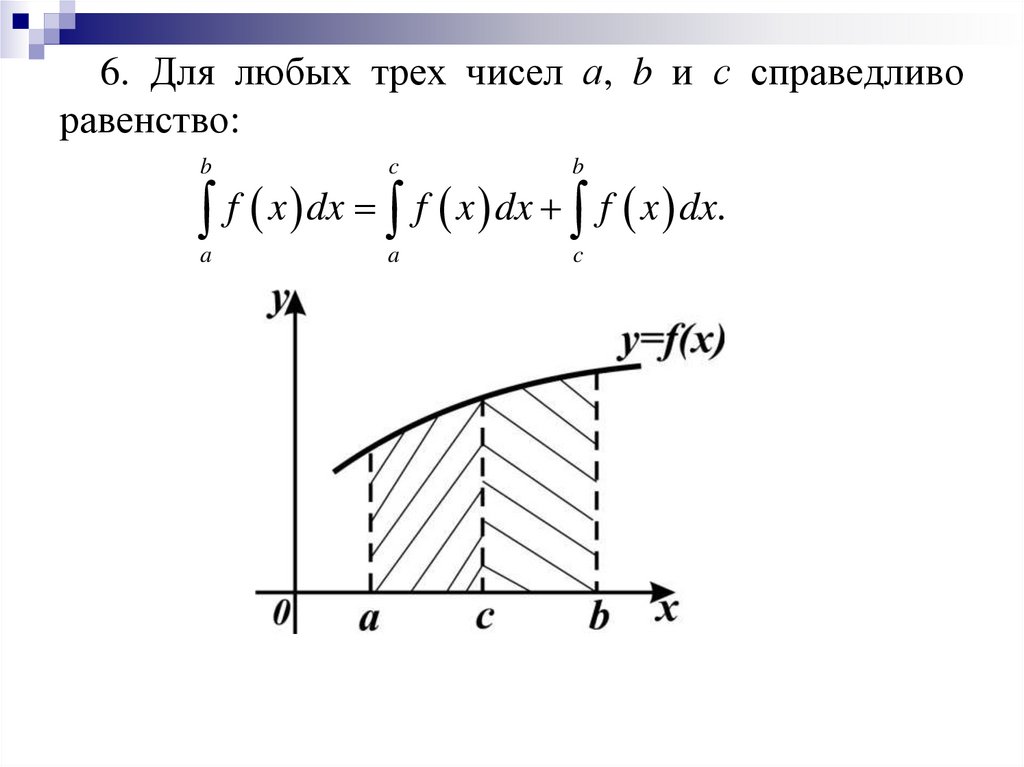
6. Для любых трех чисел а, b и с справедливоравенство:
b
c
b
a
a
c
f x dx f x dx f x dx.
14.
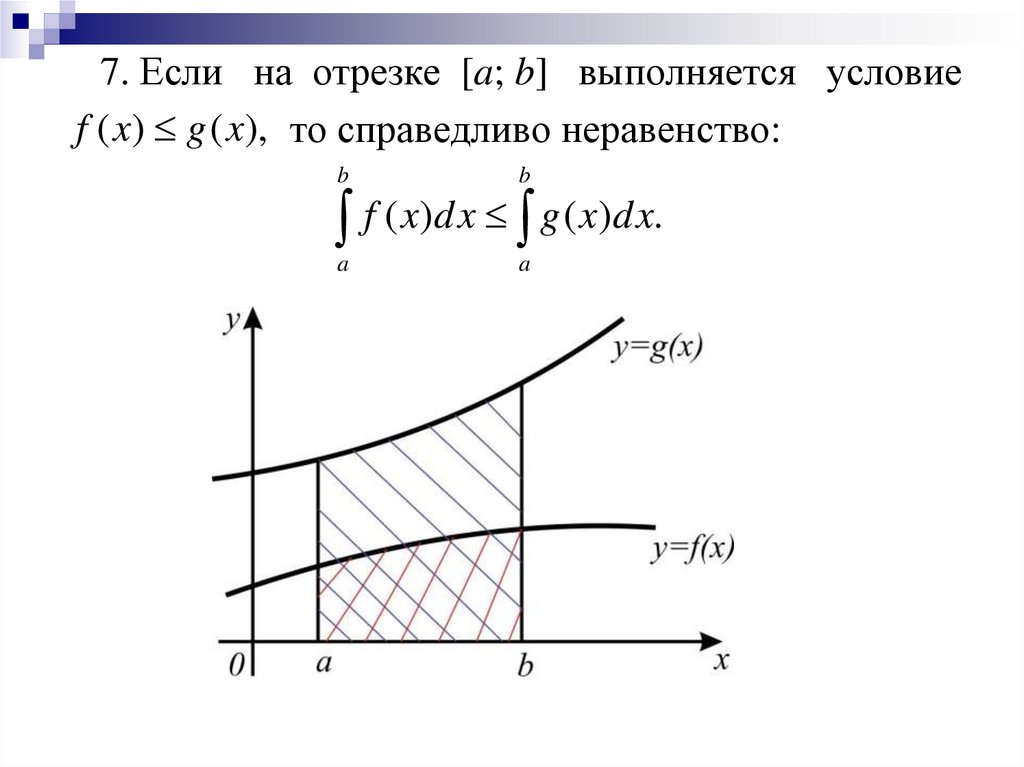
7. Если на отрезке [a; b] выполняется условиеf ( x) g ( x), то справедливо неравенство:
b
b
a
a
f ( x)dx g ( x)dx.
15.
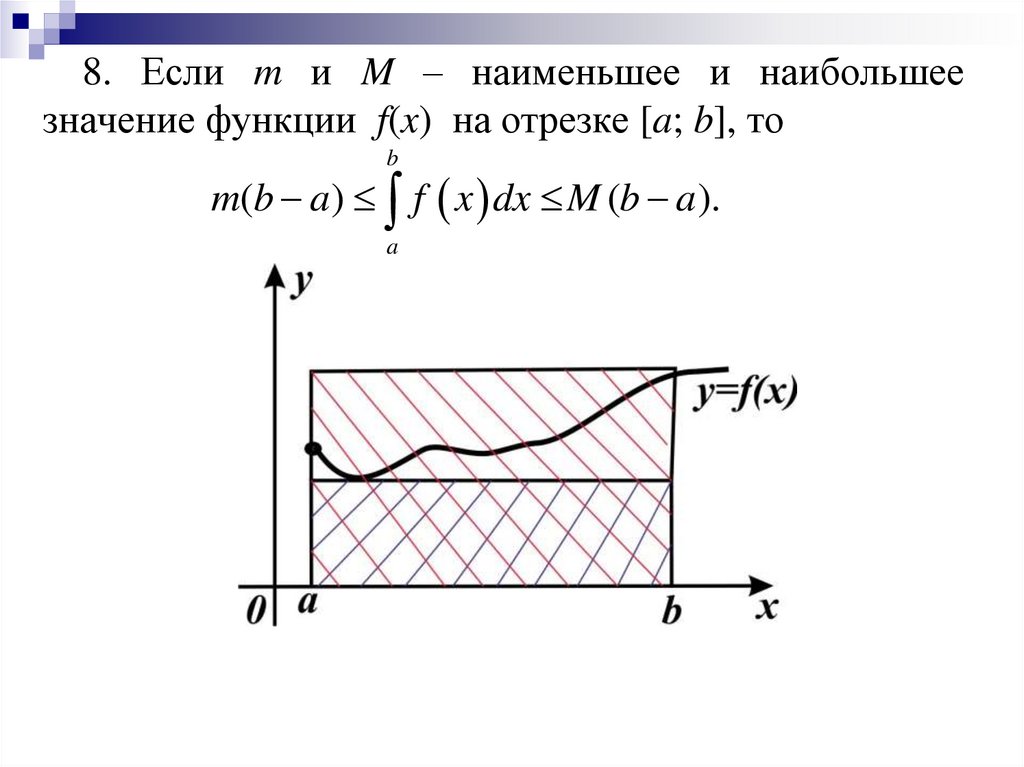
8. Если m и M – наименьшее и наибольшеезначение функции f(x) на отрезке [a; b], то
b
m(b a) f x dx M (b a ).
a
16.
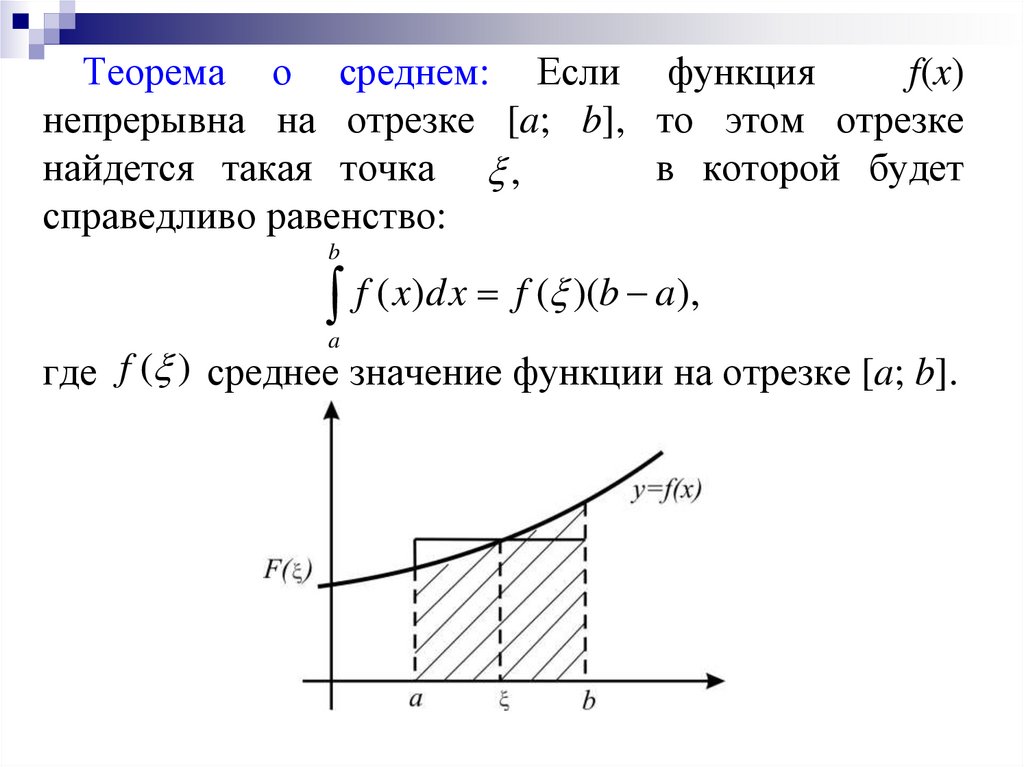
Теорема о среднем: Если функцияf(x)
непрерывна на отрезке [a; b], то этом отрезке
найдется такая точка ,
в которой будет
справедливо равенство:
b
f ( x)dx f ( )(b a),
a
где f ( ) среднее значение функции на отрезке [a; b].
17. Методы вычисления определенного интеграла
18.
Непосредственное интегрированиеТеорема: Если F(х) какая-либо первообразная
непрерывной функции f(x), то справедлива формула:
b
b
f x dx F x F b F a .
a
(1)
a
(1) называется формулой Ньютона-Лейбница.
Формула
Ньютона-Лейбница
позволяет
вычислять определенные интегралы в том случае,
когда известна первообразная подынтегральной
функции.
19.
3Пример: Вычислить интеграл x 2 dx.
Решение: 0
3
3 3
3
3
x
3
0
2
x
0 dx 3 0 3 3 9.
4
Пример: Вычислить интеграл cos 2 xdx.
0
Решение:
4
4
4
1
1
0 cos 2 xdx 2 0 cos 2 xd (2 x) 2 sin 2 x
0
1
1
1
sin sin 0 1 .
2
2
2
2
20.
Замена переменной в определенном интегралеb
f ( x)dx , где функция f(x)
Теорема: Пусть дан
a
непрерывна на отрезке [a; b]. Введем новую
переменную t по формуле x (t ) . Если
1. ( ) a, ( ) b;
2. (t ) и (t ) непрерывны на отрезке [a; b];
3. f (t ) определена и непрерывна на [a; b], то
b
f x dx f (t ) (t )dt.
a
(2)
(2) – формула замены переменной в определенном
интеграле.
21.
Замечание: При вычислении определенногоинтеграла по формуле (2) к старой переменной
возвращаться не нужно.
1
xdx
.
Пример: Вычислить интеграл
4
1 x
0
Решение:
2
t
x
,
1
1
xdx
xdx
0 1 x 4 0 1 ( x 2 )2 dt 2 xdx, x 0 t 0
1
xdx dt , x 1 t 1
2
1 dt
1
1
1
arctg t arctg 1 arctg 0 .
2
2 0 1 t
2
2
2 4 8
0
1
1
22.
5dx
.
Пример: Вычислить интеграл
0 2 3x 1
Решение:
t 3x 1, 3 x 1 t 2 ,
2
t 1
2
5
4
tdt
dx
x
, dx tdt ,
3
3
3
0 2 3x 1
1 2 t
x 0 t 1
x 5 t 4
2
23.
Под знаком интеграла стоит неправильная дробь,выделим целую часть и проинтегрируем полученное
выражение:
2 t 2 2
2
4 d t 2 2
dt dt
t
31 t 2
31
3 1 t 2
3 1
4
4
4
4
4
4
2
4
4
ln 2 t (4 1) ln 6 ln 3 2 ln 2.
3
3
3
3
1
24.
Метод интегрирования по частямТеорема: Пусть функции u ( x) и v ( x ) непрерывно
дифференцируемы на отрезке [a; b], то справедлива
b
b
b
формула:
(3)
u dv u v v du.
a
a
a
(3) – формула интегрирования по частям в
определенном интеграле.
Замечание: При интегрировании по частям в
определенном
интеграле
справедливы
все
рекомендации
по
применению
метода
интегрирования по частям в неопределенном
интеграле.
25.
1Пример: Вычислить интеграл arctg x dx.
Решение: 0
u arctg x,
dv dx,
0 arctg x dx du 1 dx, v dx x
1 x2
1
t x 1, dt 2 xdx,
xdx
xarctg x
x 0 t 1
2
1 x
0
0
x 1 t 2
2
1
1
1 dt 1
1
arctg1 ln t ln 2 ln 2.
21 t 4 2
4 2
4
1
2
2
26.
1Пример: Вычислить интеграл x e dx.
Решение: 0
Применим метод интегрирования по частям:
2 3x
1
2 3x
x
e dx
0
1
u x2 ,
dv e3 x dx,
1 3x
du 2 xdx, v e dx e
3
3x
1
1
1 3x
1 3x
1 3
2
x e
e 2 xdx e 0 xe3 x dx
3
3
3
30
0
0
2
27.
Применим еще раз метод интегрирования почастям:
u x,
dv e3 x dx,
1 3
1 3x e
3x
3
du dx, v e dx e
3
1
1
1
1
2 1 3x
1 3x 1 3 2
2
x e
e dx e x e3 x e3 x dx
3
3 3
3
9
90
0
0
0
1
1 3 2 3 2 1 3x
1 3 2 3 0
5 3 2
e e e
e e e e .
3
9
9 3
9
27
27
27
0



















 Математика
Математика








